基于传感器的室内测试轨迹系统*

张 迅，黎 伟，周建国，王 赛

(武汉大学 电子信息学院，湖北 武汉430079)

0 引 言

近年来，GPS 技术取得了巨大的发展和广泛的应用，能够实现对位置信息的记录，记录测试轨迹。但GPS 技术也存在明显的缺点［1］，例如:代价较高，设备较为复杂，存在信号难以到达的地方。目前，室内环境下的测试轨迹还没有特别成熟的方案，在进行室内测试的过程中，人们需要记录测试的轨迹，从而获得测试点的具体位置。

本文针对室内测试的环境进行了研究，设计并实现了一种基于传感器［2］的测试轨迹系统。系统体积小、成本低、功耗低、稳定性好、精度也能满足一般室内测试的需求［3］。

1 总体架构

本系统主要由三部分组成，包括传感器模块，数据采集和处理模块。传感器模块主要由三轴加速度计、三轴陀螺仪和磁强计组成，主要功能是获取所需的信息;数据采集模块主要是实现将传感器的数据读入单片机并执行相应的算法;数据处理模块是对由测试数据转换得到的位置信息进行修正。系统结构如图1 所示。

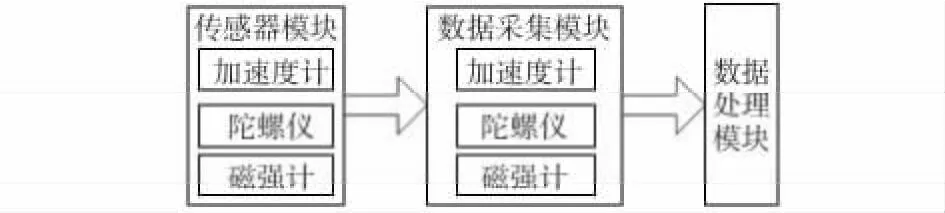
图1 系统总体框架结构Fig 1 System overall framework

2 关键技术

人在行走过程中，通常会保持一个固定的习惯步长，行走距离可视作步长和步数进行相乘。本文基于加速度传感器模块，开发了步长和步数的计量方法。

2.1 步数检测算法

在行走时，身体的各个部位，例如:手臂、腰部、腿部等的运动都会产生一定的加速度，且其值不断变化，呈现出周期性的变化规律。在各部位中腿的运动幅度最大，产生的加速度变化信息最为明显，理论上来说以腿的加速度值来检测步数最为准确。然而考虑到将测试模块绑在腿部会影响人体正常行走，因此，本文将测试模块放置在人体的腰部。在行走时，腰部会产生三个方向的加速度变化，测试中采集三个方向的加速度。通过大量测试发现，三个方向的加速度均呈现一定的周期性，其中，Z 轴的周期性最为明显，其加速度曲线如图2 所示。

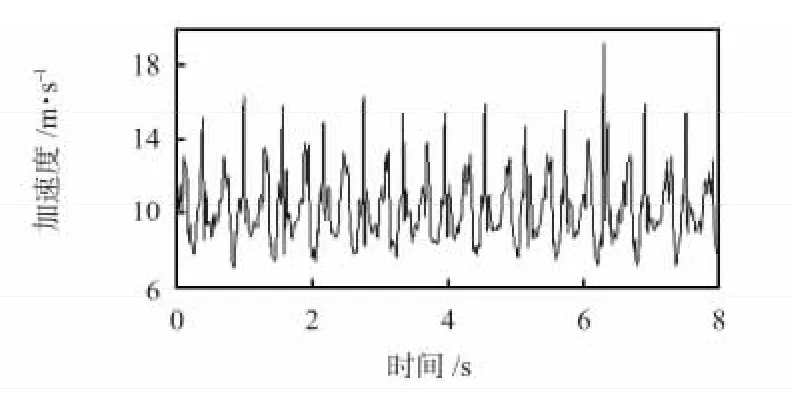
图2 Z 轴加速度曲线Fig 2 Z-axis acceleration curve

如果去掉噪声的干扰，Z 轴的加速度变化规律类似于正弦曲线，因此，使用Z 轴的加速度来进行计步会简单、准确一些。由于人行走的频率是小于5 Hz 的，因此，加速度的变化频率也应低于5 Hz，频率高于5 Hz 的信号视作为噪声。在Matlab 中，用Hamming 窗设计通带截止频率为5 Hz的FIR 直接型低通滤波器［4］来对加速度曲线进行去噪处理，得到的曲线见图3 所示。

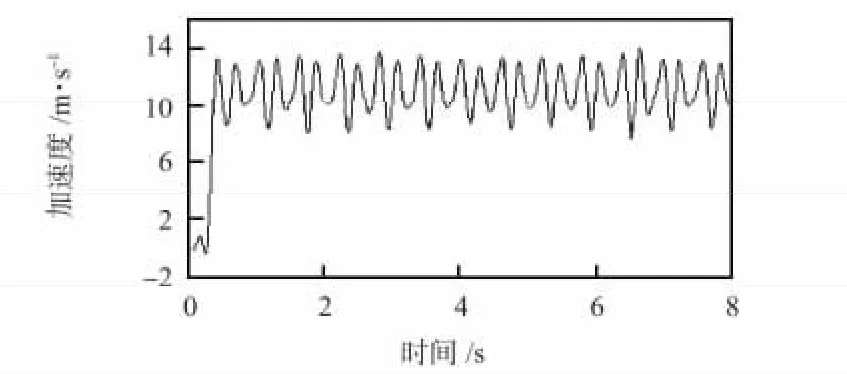
图3 滤波后Z 轴的加速度曲线Fig 3 Z-axis acceleration curve after filtering

对比滤波前后的加速度曲线可以发现滤波后的加速度具有明显的周期性，每一个加速度的峰值和低谷就对应着一步。检测步数也变得更简单了，只需要找出加速度的峰值和低谷就知道了行走的步数。需要注意的一点是，由于峰值和低谷是成对出现的，所以，只要得到峰值的数目或者是低谷的数目就可以了。但为了计算步长，需要将峰值和低谷都检测出来。

检测峰值低谷的步骤如下:

1)初始设置加速度的最大值和最小值Amax=Amin=A［1］，i=2，raise=0，fall=0。

2)如果A［i］大于Amax，则更新Amax的值为A［i］并让raise 赋值为1，说明这是一个上升过程;反之，说明这可能是一个峰值;如果raise 等于1，则判断该点为峰值点并且将Amin设置为Amax，同时让raise=0，fall=1，表明这是一个下降过程。

3)在fall=1 的条件下，如果A［i］小于Amin，则更新Amin的值为A［i］;反之，说明这是可能是一个低谷，如果Amax－Amin大于某个阈值，则判断该点为低谷点，并且将Amax设置为Amin，将fall 变为初始值0;反之，则认为这是一个抖动，同时也将Amax设置为Amin。

4)将i 分别赋值3－N，N 为加速度数据的总个数，重复步骤(2)，(3)。

2.2 步长计算

在匀速行走时，步长主要取决于人的腿长，人行走时的运动模型见图4 所示。在图4 中，人首先抬起右脚，垂直方向加速度开始增大，人的臀部也开始上升;当左腿处在垂直方向时，加速度达到最大，臀部也到最高点;之后加速度会逐渐减小，到右腿着地时，加速度减小到最小值。由图可知

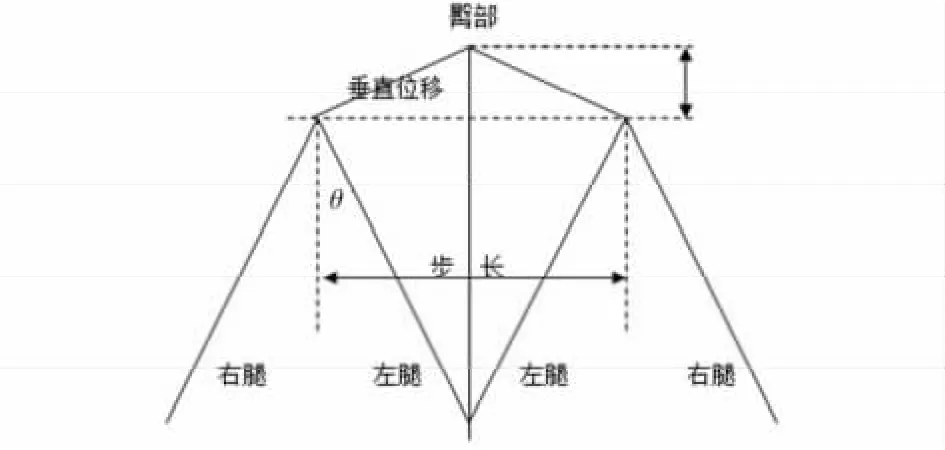
图4 步行时臀部和腿部运动示意图Fig 4 Hip and leg movement during walking

α 是个很小的角，可以将其看作一个常数。这里采用AD 公司的应用笔记［5］中的一个简化公式来计算步长

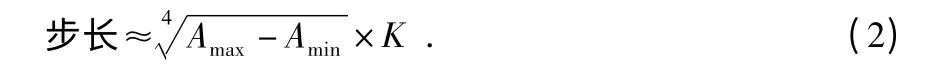
其中，Amax为单次跨步过程中垂直方向加速度的最大值，Amin为单次跨步过程中垂直方向加速度的最小值，K 为单位转换所用的常数。

2.3 方向检测算法

因单独利用磁强计难以获得较高精度的方向［6］，而陀螺仪具有短时精度高，受外界干扰小等优点，正好和磁强计的特点互补。

本文应用卡尔曼滤波，对磁强计和陀螺仪的角度进行处理。用陀螺仪的数据作为预测量来预测人体转过的角度，然后用磁强计的数据作为观测量来实时地对陀螺仪进行修正，这样就能提高偏转角度的准确性。以Xk表示人行走的偏转角度，Uk为陀螺仪的输出，Zk为通过磁强计计算的角度，Xk即为系统的状态量，Zk为系统的观测量。根据卡尔曼滤波的原理得到系统的状态方程如下

进一步可以推出卡尔曼的5 个方程如下

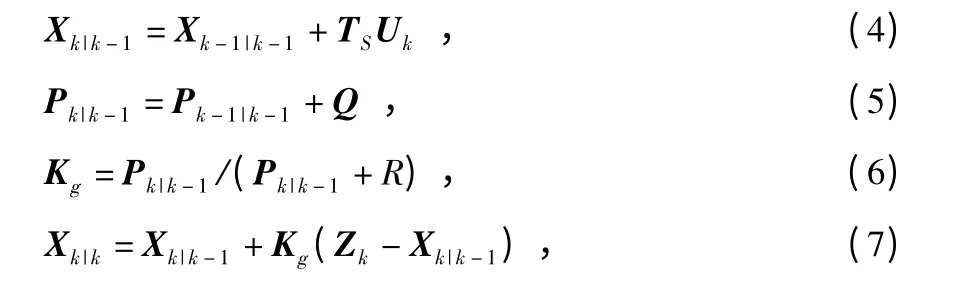
这是卡尔曼滤波应用在一维的情况，上面5 个方程中的量都是单个的数，不是矩阵，省去了矩阵运算，也降低了对微处理器的运算能力的要求。

3 算法流程

3.1 数据采集

数据采集的流程图如图5 所示。

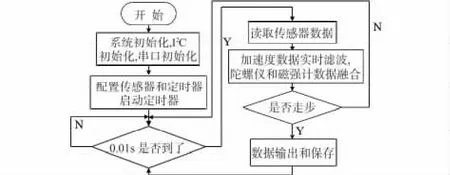
图5 数据采集流程图Fig 5 Data acquisition flowchart

首先进行系统的初始化主要是初始化系统的时钟，然后对I2C 进行初始化，使单片机能和传感器模块正常通信，初始化串口。然后对传感器进行初始化，主要是对传感器的一些寄存器进行配置来选择系统需要的工作方式。接下来设置一个定时时间为0.01 s 的定时器并启动定时器，每到0.01 s 系统便会中断一次。0.01 s 到了，主程序便会读取传感器的数据［7］，对加速度数据进行低通滤波，利用陀螺仪数据计算0.01 s 内转的角度，并与磁强计计算的角度进行卡尔曼滤波。最后根据滤波后的加速度值来进行跨步检测，如果走了一步，就通过串口输出这一步的长度和偏转角度。

3.2 数据处理与修正

在实际的测试过程中传感器经常会受到干扰和测试人员测试的不规范性，导致测试的准确性下降，使测试轨迹失真。正常测试的情况下，人的行走轨迹是不可能与墙体坐标有交点的，如果测试的不准确性可能会导致人体的行走轨迹与墙体存在交点。为了提高测试轨迹的准确性，采用基于多叉树搜索［8，9］的方法对测试轨迹进行匹配修正。

其主要步骤如下:

1)根据测试的起点和测试的数据获得位置的坐标信息，从而获得行走轨迹，判断没经过处理的轨迹与墙体是否存在交点，如果不存在，说明测试轨迹较为准确，对得到的坐标信息进行保存;否则，进行下面的步骤。

2)算出测试轨迹的平均步长，根据平均步长，设置轨迹匹配步长的合理范围。

3)找出测试数据中的特殊点，包括起始点和转弯点。

4)根据设置的步长范围的最小值获得下一个特殊点p－next 的坐标，当前特殊点p 为当前轨迹的起点，p－next 为当前轨迹的终点。

5)判断当前轨迹与墙体有没有交点，如果没有交点，则进行下面的步骤;否则，如果当前轨迹的步长没有到达步长范围的上限，则缓慢增大当前轨迹的步长，直到当前轨迹与墙体没有交点为止。重复步骤(4)，(5)，并把p－next 作为下一条路径的起点。

6)如果当前轨迹的步长范达到了步长范围的上限，则当前的特殊点回到上一个特殊点p－before;再重复步骤(3)～(5)。如此反复，直到当前轨迹的终点和测试轨迹的终点重合为止。轨迹匹配流程图如图6 所示。

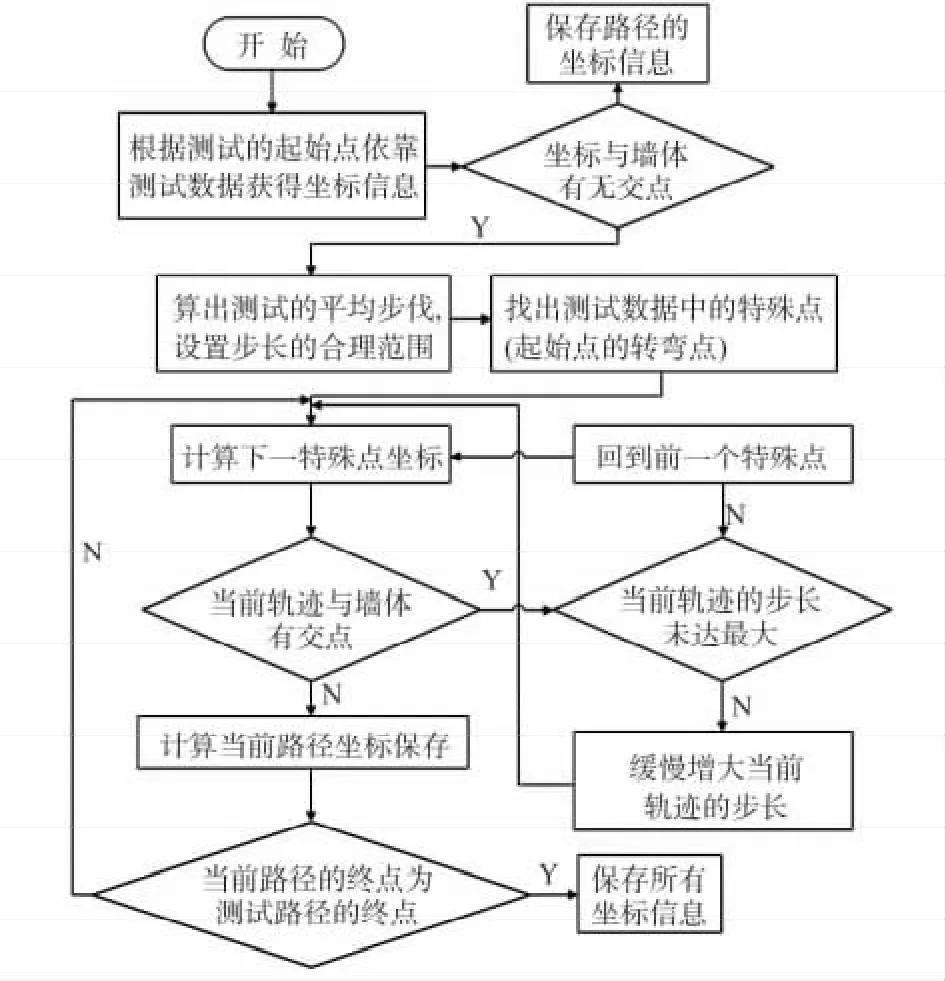
图6 轨迹匹配流程图Fig 6 Trajectory matching flowchart

4 测试结果分析

为了测试最终形成的测试轨迹的准确性，进行了多次测试，现以在福州市金山特易购三楼的测试为例来说明。真实的测试轨迹如图7，本系统所画轨迹如图8。

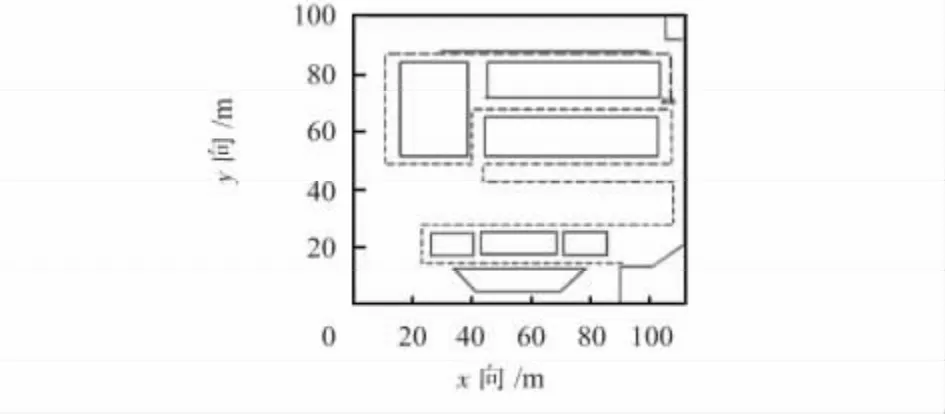
图7 原始测试轨迹图Fig 7 Original test trajectory

通过对比图7 和图8 可以看出:两者的轨迹匹配程度较高，系统生成的轨迹能够反映测试轨迹。

5 结 论

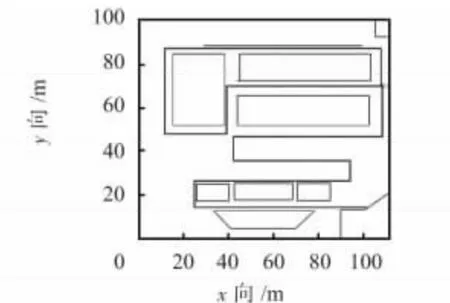
图8 系统生成的轨迹图Fig 8 Trajectory generated by system

本文以室内测试的过程中难以收到GPS 信号为背景，研究并实现了一种完全依靠传感器获得测试轨迹的系统。本系统通过加速度计来计算行走距离，并通过磁强计和陀螺仪来确定运动方向。系统硬件设备简单，成本低廉，能够实时获得人的位置信息。最后通过匹配算法对位置信息进行合理的修正，提高了测试轨迹的准确性。

［1］ 汪 苑，林锦国.几种常用室内定位技术的探讨［J］.中国仪器仪表，2011(2):54－57.

［2］ 王淑华.MEMS 传感器现状及应用［J］.MEMS 与传感器，2011，48(8):516－519.

［3］ Hanse J G.Honeywell MEMS inertial technology＆product status［C］∥ION NTM 2004，San Diego，California，USA，2004.

［4］ 何昆鹏.MEMS 惯性器件参数辨识及系统误差补偿技术［D］.哈尔滨:哈尔滨工程大学，2009.

［5］ Weinberg Harvey.Using the ADXL202 in pedometer and personal navigation applications［Z］.Analog Devices Inc，2002.

［6］ 宋丽君.基于MEMS 器件的航向姿态测量系统的研究［D］.西安:西北工业大学，2007.

［7］ 赵 琳.MEMS 惯性器件的数据采集与误差分析技术研究［D］.哈尔滨:哈尔滨工程大学，2009.

［8］ 任晶晶，郭宇明.一种改进的进路搜索方法［J］.仪器仪表用户，2005(1):70.

［9］ 王 敏，赵晓雷.基于遍历搜索二叉树中最长路径的算法研究［J］.软件技术，2010(8):54－56.