基于CPM法的早时标网络计划时间参数算法应用

■杨 波 ■黄冈师范学院，湖北 黄冈 438000

早时标网络计划是带有时间坐标的双代号网络计划，以时间坐标为尺度绘制网络计划，用工作箭线的水平投影长度表示其持续时间的多少，同时以波形线表示其时差，它是以各项工作的最早开始时间为依据编制的，即各节点对应的时刻就是以该节点为起点节点的工作的最早开始时间。

1 早时标网络计划图三要素与时间参数之间的关系

早时标网络计划图三要素包括节点、箭线和线路。

(1)节点表示工作的开始或完成时刻，起连接作用，节点中心必须对准相应的时标位置。

(2)箭线与其两端的节点表示一项工作，箭尾节点对应该工作的开始时刻，箭头节点对应该工作的完成时刻，实箭线长度与时间有关，以水平投影长度表示工作的持续时间，波形线水平投影长度表示自由时差的多少。箭线与工作之间的关系如下:①紧前工作与内向箭线。相对于某一项工作(以下称本工作)来看，紧挨在其前边的工作称为紧前工作，即表示紧前工作的箭线箭头和完成节点与本工作的开始节点和箭线箭尾紧挨着，且表示同一时刻，如图1所示，图中B工作为本工作，紧前工作为A工作，表示A工作的箭线称为j节点的内向箭线;②紧前工作与内向箭线。同理可知，图中A工作为本工作，紧后工作为B作，表示B作的箭线称为j节点的外向箭线。

图1 箭线与工作的关系

(3)线路是指网络图中从起点节点开始，沿箭头方向顺序通过一系列箭线与节点，最后达到终点节点的通路，其中无波形线的通路持续时间最长，且为关键线路，其时间代表整个网络计划的计划总工期，关键线路上的工作称为关键工作。

2 基于CPM法的早时标网络计划的工作时间参数算法

(1)CPM法即关键路径法(Critical Path Method)是一种基于数学计算的项目计划管理方法，将工程项目分解成为多个独立的主导工作并确定每个工作的持续时间，然后根据工艺和组织逻辑关系表达工作关系，从而能够计算工程项目的工期及工作时间参数。

(2)基于CPM法的时间参数算法

①计算步骤及内容。

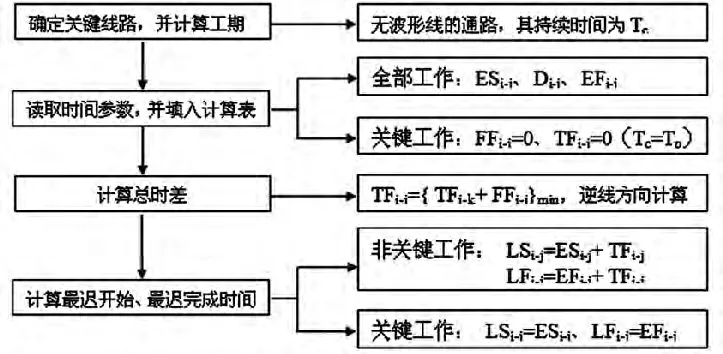
图2 基于CPM法的时间参数算法步骤及内容

②总时差计算技巧。依据 TFi－j={TFj－k+FFi－j}min，逆线方向计算。如表1。特例一，总时差为0的情况。①当Tc=Tp时，关键工作的总时差为0。②无波形线的工作且紧后工作中有关键工作，其总时差为0。特例二，总时差等于波形线水平投影长度的情况。有波形线的工作且紧后工作中有关键工作。

表1 工作总时差计算技巧

3 基于CPM法的早时标网络计划的工作时间参数算法应用

某混凝土工程，分成三个施工段，计划工期19天，其早时标网络计划，如图3，时间参数计算如下:

图3 某混凝土工程早时标网络计划

(1)确定图3－1中关键线路，用节点编号表示，即①②④⑤⑥⑦⑨⑩，计算工期19天。

(2)读取各工作的最早开始、持续时间、最早完成、自由时差、关键工作的最迟开始、最迟完成及总时差，填入表2中。

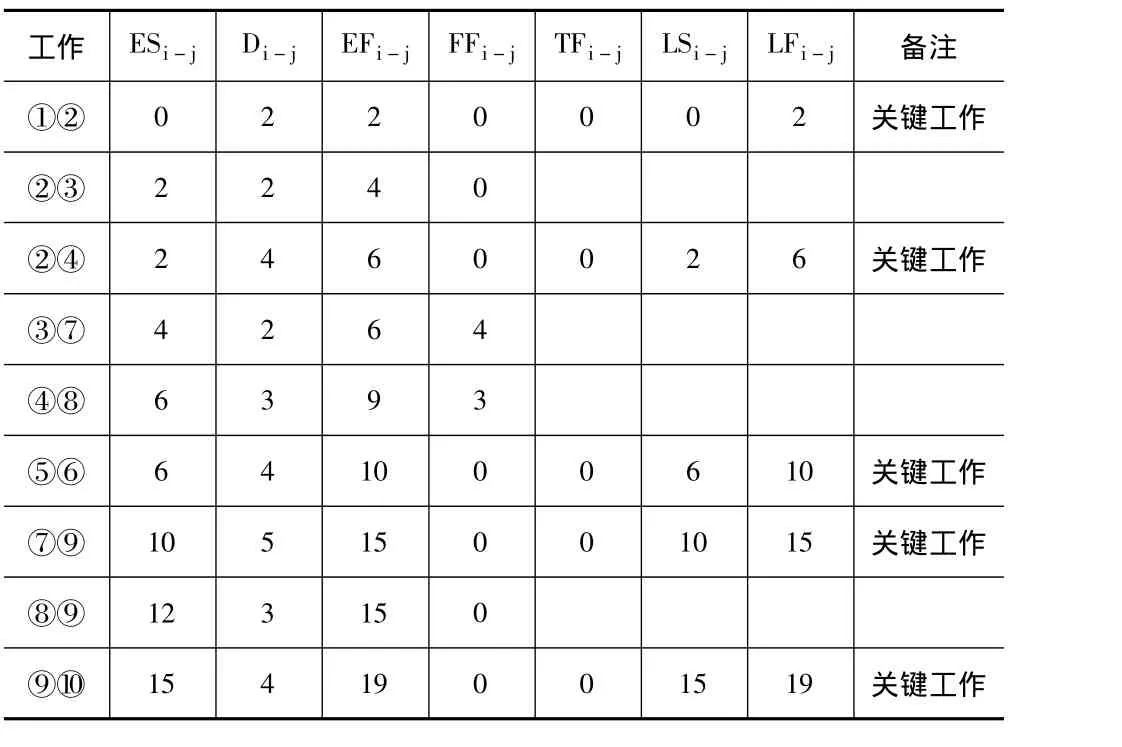
表2

(3)计算非关键工作总时差。②③工作的紧后工作仅有③⑤工作，先计算③⑤工作的总时差，其紧后工作仅有⑤⑥工作，符合特例二，则TF3－5=FF3－5=2，再依据表2－1计算②③工作的总时差，则 TF2－3=TF3－5=2;⑧⑨工作的总时差计算，符合特例一，则TF8－9=0;③⑦工作的总时差计算，符合特例二，则TF3－7=FF3－7=4。

(4)计算非关键工作最迟开始、最迟完成

4 结论

通过基于CPM法的早时标网络计划的工作时间参数算法应用，改进了计算步骤，首先明确了关键工作的时间参数，能较大的简化计算，运用客观的规律，能快速的得出非关键工作的总时差，对进度检查及调整工作提供依据。

［1］陈志明.时标网络计划的应用研究［J］.安徽农业科学，2012(36):17445－17447，17454.

［2］叶平.基于CPM的甘特图应用研究［D］.浙江工业大学，2012.

［3］罗明.网络计划时间参数判定的一个简易方法［J］.建设监理，2001(03):44－46.

［4］刘友平.网络计划自由时差与总时差的关系及其计算［J］.基建管理优化，2008(01):15－18.