电力系统传感器网低复杂度匹配滤波器设计*

黄少伟，杨云涛，许知博

(1.清华大学 电机系 电力系统国家重点实验室，北京100084;2.陕西省地方电力(集团)有限公司，陕西 西安710061)

0 引 言

电力系统传感器网服务于电网运行、维护和管理，在近年来得到了广泛的发展［1，2］。随着无线技术的不断进步，其在电力系统传感器网中也得到了较大的关注和应用。目前，已经相关研究关注GPRS［3］、WiMAX［4］等在该领域的应用。然而，这些研究并未对已有无线技术从电力系统传感网的具体特点进行优化。事实上，由于电力系统传感器网需要长时间运行，降低接收机复杂度可以有效降低能量消耗。因此，本文研究在电力系统传感器网中无线接收机的低复杂度匹配滤波器设计，以期缓解系统的实现压力。

在无线收发机中，为了节省传输带宽，发送端需对符号级的信号升采样后进行低通成型滤波;相应地在接收端，为了使抽样时刻的信噪比(signal-to-noise ratio，SNR)最大，需对过采样信号进行匹配滤波［5，6］。为了避免波形成型和匹配滤波引入新的码间串扰(inter symbol interference，ISI)，相关滤波器都常选用根升余弦(root raised cosine，RRC)滤波器［7～9］。然而，实现RRC 匹配滤波运算需要较多的乘法器资源，直接应用于电力系统传感器网中会对资源和功耗都带来挑战。

本文提出采用方波代替RRC 波形来实现匹配滤波，省去了乘法运算，大大降低了实现复杂度，更易满足低功耗等设计需求。此外，方波匹配滤波器的最佳长度接近于过采样倍数，远小于传统的匹配滤波器长度，这也进一步降低了运算量，节省了系统资源。误比特率(bit error rate，BER)性能仿真结果表明，方波匹配滤波相比RRC 匹配滤波没有明显的性能损失，从而进一步保证了这种方法的有效性与可用性。

1 系统模型

本文考虑的系统模型如图1所示。在发送端，将经过编码调制后的数据符号x(n)进行N 倍升采样得到X0(n)，然后再对X0(n)通过响应为H(n)的成型滤波器实现波形成型，并且得到X(n)。常用的波形成型滤波器为RRC 滤波器，其形式为

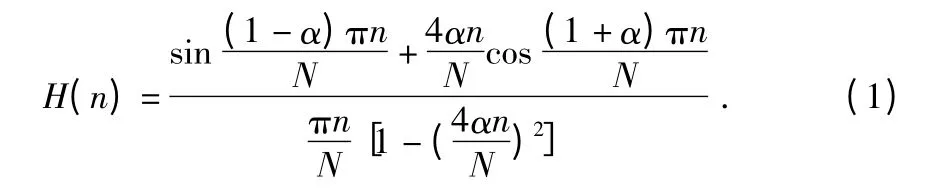
其中，α 为滚降系数，且0≤α≤1，通过改变α 的大小可以调整发送信号的带宽。理论上，RRC 滤波器是无长限的，无法得到应用，而用于系统实现的RRC 滤波器是以主瓣为中心截取理论值的一部分。如果截取的RRC 滤波器长度为K 个符号周期，那么H(n)的阶数为NK+1，如此，波形成型可以表达为

由于X0(n)中每N 个采样点只有一个非零值，式(2)中卷积运算的项数其实是比较少的;此外，X0(n)中的非零值即x(n)是调制星座点，组成形式简单，特别是对于BPSK或QPSK 信号x(n)的IQ 两路非零值都为±1，波形成型可由加法实现。

成型后的信号X(n)通过D/A 转换器DAC 后得到待发送的模拟信号x(t)。经过信道和噪声的影响后，接收到的模拟信号记为y(t)，随后A/D 转换器(ADC)对y(t)进行N 倍符号速率过采样得到数字信号Y(n)。为了最大化最佳采样点的SNR，需先将Y(n)通过匹配滤波器h(n)得到Y0(n)。匹配滤波器h(n)应该为波形成型滤波器H(n)的镜像，同时为了满足因果性还带有一定的时延。匹配滤波的实现过程如式(3)所示

由于RRC 滤波器是对称的，所以，h(n)与H(n)实际上是相同的。在匹配滤波之后，对Y0(n)进行N 倍下采样抽出最佳采样点得到符号级数据y(n)，即y(n)=Y0(nN)。

与波形成型的输入X0(n)不同，匹配滤波的输入Y(n)由于经历了信道和噪声的影响，具有较大的随机性。一方面Y(n)不会有规律地出现零值;另一方面，Y(n)具有较大的动态范围，其取值是多比特量化后的结果。因此，RRC匹配滤波不同于波形成型，在硬件实现时难以进行优化。

从式(3)中可以分析得到，实现RRC 匹配滤波共需要NK+1 个乘法器和一个输入为NK+1 项的加法器。如果是R 路并行传输，那么所需资源还将是以上结果的R 倍。然而，实际硬件中的资源特别是乘法器资源是十分有限的，而且这些有限的资源也主要是分配给均衡、译码等其它更为复杂的数字信号处理模块，所以，这种传统的RRC 匹配滤波结构并不利于系统低复杂度低功耗实现和小型化集成。

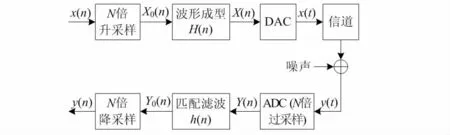
图1 系统模型框图Fig 1 Block diagram of system model

2 基于方波的匹配滤波器

对于乘法器的实现，如果输入的2 个因数中有一个取值为0 或±1，那么复杂度相对较低，如波形成型中的待成型信号就具有这种特征。如果乘法的2 个因数均是多比特的量化数据，那么实现的复杂度相对较高。RRC 匹配滤波器的滤波器系数和输入信号均是有一定动态范围的多比特量化数据，所以，乘法运算的复杂度较高。为了降低RRC匹配滤波器的实现复杂度，本文用方波来近似RRC 波形，即将RRC 波形中靠近主瓣中心位置L 个点的幅度设成恒定值，而将其它位置的幅度设置为0。

图2 所示为RRC 波形示意，可以看作为发送端波形成型后信号的包络形状。如图2 所示，原来的脉冲信号经过波形成型后在时域上无限展宽，而且各个符号还会相互交叠形成ISI。波形成型将符号能量分散到不同的采样点上，而RRC 匹配滤波是要分散到这些不同采样点上的符号能量集中起来，以使最佳采样点的SNR 最大且消除最佳采样点上的ISI。当采用方波来近似RRC 波形做匹配滤波时，由于不考虑各个采样点上的能量差异，只能搜集主瓣中靠近中心位置的若干个点的能量。首先，主瓣中心位置附动态范围较小，用相等的幅值来近似较合理;其次，对于一个符号其能量也主要分布在主瓣中心位置的少数点上，而其它点所占据的能量较少;再次，在主瓣中心位置其它相邻符号的干扰相对较小，可以保证匹配滤波后有较小的ISI。综上，采用方波来实现匹配滤波具有较强的可行性。

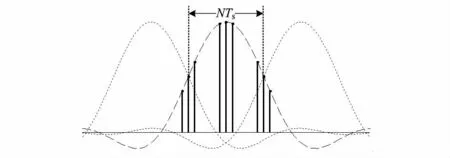
图2 RRC 波形示意图Fig 2 Schematic diagram of RRC waveform

方波匹配滤波器的长度L 与过采样倍数N 相关，如图2所示，在主瓣内当前符号比相邻符号能量更强的时间窗口长度为NTs，其中，Ts为采样点间的时间间隔。显然，方波匹配滤波器的时间宽度应该在NTs之内，而更长的宽度不但会带来更大的ISI，而且能额外搜集到的符号能量也非常有限。对于数字信号，NTs时间宽度内的采样点数为N-1或N。当在NTs时间窗口的边缘处存在采样点时，该窗口内的采样点数为N-1(不考虑上述窗口边缘的采样点);否则，为N 点。对于实际系统，边缘处是否存在采样点是受定时偏差等因素影响的。总之，当ADC 过采样倍数为N 时，方波匹配滤波器的最佳长度L 将可能取为N-1或N，这远小于RRC 匹配滤波器的长度NK+1。

通过采用方波来近似匹配滤波器时，方波的幅度可选择成合适的常量。为了实现简单，可以将方波的幅度设置成为1，如此，匹配滤波的实现可以简化为

式(4)所示的方波匹配滤波器只需由一个输入为L 项的加法器来实现。因此，比起传统的RRC 匹配滤波器，方波匹配滤波器不但节省了所有的乘法器，而且加法器的输入项数也大大得到了降低。

对于并行匹配滤波的情况，相邻支路的加法输入项有许多相同。如果式(4)中输入为L 项的加法采用多级实现，对于多路并行情况相邻支路的方波匹配滤波的加法器还可以通过强度压缩技术实现共用，进一步存在资源优化的空间。如此，对于R 路并行方波匹配滤波器，其资源复杂度小于单路方波匹配滤波器的R 倍。然而，传统RRC 匹配滤波器的加法输入项是先经过乘法运算得到的，相邻支路不存在相同的加法器输入项，所以，R 路并行RRC 匹配滤波器的资源复杂度等于单路RRC 匹配滤波器的R 倍。

3 仿真结果与性能分析

本文部分在Matlab 平台上进行仿真，对比传统RRC 匹配滤波和方波匹配滤波器的BER 性能。仿真中调制方式采用QPSK，信道代表性地选择为高斯白噪声(additive white Gaussian noise，AWGN)信道，过采样倍数N 取为8，波形成型RRC 滤波器滚降系数取为0.5，RRC 滤波器截取的长度为K=6 个符号。

图3 描述了无定时偏差即Δt=0 时不同情况下的BER性能。从图中可以看到，采用RRC 传统匹配滤波时，BER性能与QPSK 调制理论性能几乎一致，这体现出了RRC 匹配滤波在这种情况下的优越性。当采用方波实现匹配滤波时，BER 性能相比理论QPSK 及RRC 匹配滤波会有一定的损失，不过，只要方波匹配滤波器的长度L 选择合适，性能损失可以控制在较低水平。当L 选择为7，8 或9 时，BER性能损失均在1 dB 范围内。

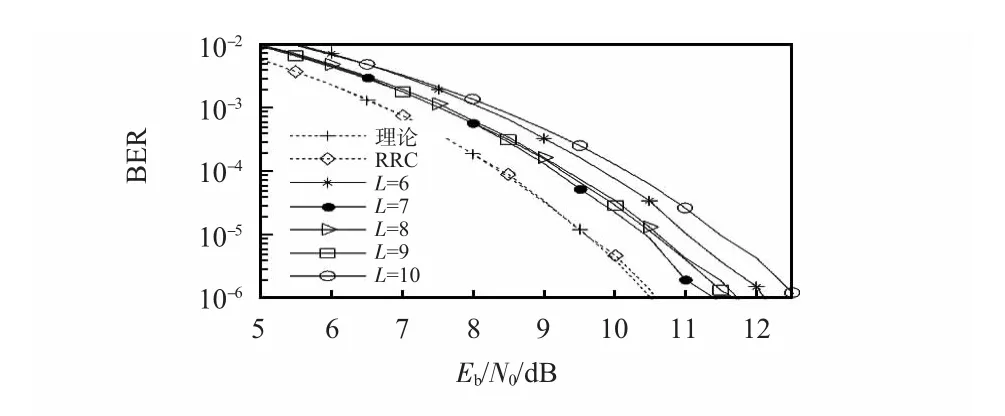
图3 无定时偏差时的BER 性能Fig 3 BER performance without timing deviation

从图3 中可以看到，在过采样倍数N=8 且Δt=0 的情况下，方波匹配滤波器的长度L=7 时可以获得最佳的BER性能。在这种情况下，如第二部分所述的主瓣中心NTs时间窗口内有7 个采样点，且窗口边缘有2 个采样点。当L小于7 时，匹配滤波所搜集符号的最佳采样点上的能量不够，即相应的SNR 较小，因此，BER 性能相对较差，如图中L=6 的情况。当L ＞7 时，相比L=7 的情况，虽然最佳采样点能够搜集到更大的信号能量，但同时也会引入较强的ISI，因此，BER 性能相比L=7 并不能获得增益。

图4 给出了定时偏差0.5 个采样点即t=0.5Ts时不同情况的BER 性能曲线。可以看到，在定时偏差影响下，传统的RRC 匹配滤波相比QPSK 理论的BER 性能有一定损失。采用方波匹配滤波时，在L=8 时BER 性能接近于RRC 匹配滤波。对比图3 和图4 可以看出，相对于RRC 匹配滤波，方波匹配滤波的BER 性能受定时偏差的影响较小。

图4 定时偏差0.5 个采样点时的BER 性能Fig 4 BER performance with timing deviation of 0.5 sampling point

如图4 所示，在N=8 且t=0.5Ts时，方波匹配滤波器长度L 取为8，即等于过采样倍数时可以获得最佳性能。此时，如第3 部分所述的主瓣中心NTs时间窗口内有8 个采样点，且边缘处不存在采样点。在这8 个采样点中主瓣对应符号的能量均强于相邻符号，因此，L 取为8，可以保证ISI 较小的同时获得较大的最佳采样点上的SNR。同样，当L ＜8 时，匹配滤波后最佳采样点不能够获得足够的SNR，而当L ＞8 时又会引入较大的ISI。

综上所述，相比传统的RRC 匹配滤波，方波匹配滤波器不仅大大降低了实现复杂度，而且，BER 性能接近于传统RRC 匹配滤波，从而保证了方波匹配滤波的有效性，适合应用于电力系统传感器网的无线传输。

4 结 论

针对电力系统传感器网，本文提出采用方波来实现匹配滤波。相比传统RRC 匹配滤波器，方波匹配滤波器不但于方波的节省了乘法器资源，而且阶数远小于RRC 匹配滤波器。基匹配滤波器大大降低了资源需求及实现复杂度，对于电力系统传感器网的无线传输有较大的应用价值。此外，方波匹配滤波的BER 性能接近于RRC 匹配滤波，表明了该方法的有效性。

［1］ Weedy B M，Cory B J，Jenkins N，et al.Electric power systems［M］.Chichester:John Wiley＆Sons Ltd，2012.

［2］ 陈守强，肖蓉川，肖继学.电力智能传感器中的信号处理研究［J］.传感器与微系统，2008，27(11):38-40.

［3］ 崔秀玉，王志勇，王成祥.GPRS 技术在电力系统通信中的应用［J］.电力系统通信，2004，25(8):3-4.

［4］ 陈 蕾.WiMAX 技术及其在电力系统通信中的应用［J］.电力系统通信，2007，28(7):46-48.

［5］ Turin G L.An introduction to digitial matched filters［J］.Proceedings of the IEEE，1976，64(7):1092-1112.

［6］ Sklar B.Digital communications［M］.New Jersey:Prentice Hall PTR，2001.

［7］ Boray G.Design of digital filters for communication systems［C］∥IEEE International Conference ICASSP’87，1987:2101-2104.

［8］ 张会生，王效洪，耿光辉.基于FPGA 实现根升余弦滤波器的研究［J］.无线通信技术，2005(2):46-49.

［9］ 凌云志.基于DSP 实现根升余弦滤波器的研究［J］.国外电子测量技术，2006，25(1):8-10.