基于光伏预测的微电网能源随机优化调度*

李鹏梅，臧传治，李鹤鹏，李忠文，杨建宏

(1.中国科学院 沈阳自动化研究所 中国科学院 网络化控制系统重点实验室，辽宁 沈阳110016;2.中国科学院大学，北京100049;3.内蒙古上都发电有限责任公司，内蒙古027200)

0 引 言

微电网能源优化调度系统通过综合考虑微电网内部各单元特性，优化微电网中现有分布式发电单元的出力和储能单元的充放电管理，在满足功率平衡、负荷需求、出力限制等前提下，实现发电成本、温室气体排放的最小化，最终满足综合效益最优原则。

对微电网的能源优化调度研究已经有很多［1～5］，但是基本处于初步阶段，相对而言技术还不成熟。其中，大部分是基于确定性方法，其忽略或简化了不确定性因素的影响。相比于确定性的优化调度模型，随机规划方法提供了更为强大的优化方案［6～10］。本文是提出了一种基于光伏发电预测的不确定性的随机规划调度模型，更符合微电网系统运行中的实际情况，调度结果也可有效地减少不确定性带来的经济损失与各种风险。

1 随机期望值规划模型概述

期望值模型是指对于包含随机变量的函数，在满足期望约束的条件下，寻求目标期望值最优的一类建模方法［11］，是最简单、最常用的随机规划模型，模型形式如下

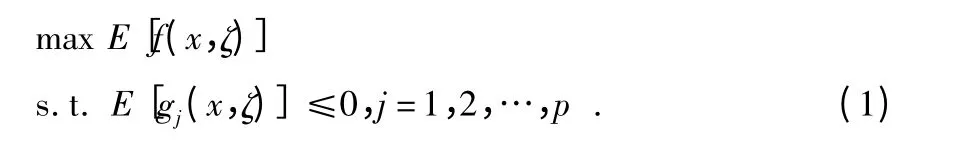
其中，x 为决策变量，ζ 为随机变量，f(x，ζ)为目标函数，而gj(x，ζ)是一组随机约束函数，j=1，2，…，p。

2 光伏发电的不确定性建模

2.1 分布拟合

光伏发电的随机性可认为主要来自于预测误差的不确定性，为了分析预测误差的不确定性，需要应用统计分析方法建立光伏发电预测误差的概率模型，用符合某个概率密度分布函数的随机变量来进行拟合。通过统计分析发现正态分布可较好地描述光伏发电预测误差的随机变化规律。正态分布的密度函数可表示为

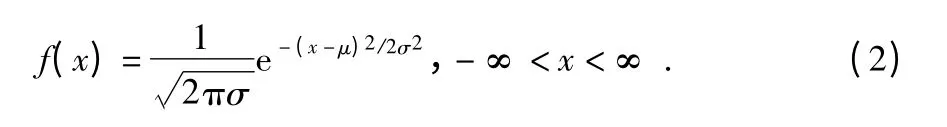
2.2 情景生成

情景生成是将随机变量的概率分布以不同情景的形式表示，并赋予其不同的情景的一定概率，这种方法可大大简化随机规划模型的求解过程，使之避免复杂积分运算。其中，Monte Carlo 模拟是情景生成的一种有效的方法，其基本思想是从给定的概率分布中抽取随机变量，通过大量随机试验，利用概率论解决问题的一种数值方法。本文采用Monte Carlo 模拟方法生成光伏发电预测误差的情景集，通过将生成的预测误差情景加上预测的光伏发电量，可以得到未来一段时间内光伏发电量的情景集，如图1 所示，10 个随机情景相应的概率如表1 所示。

表1 产生的不同情景的概率Tab 1 Probability of generated different scenarios

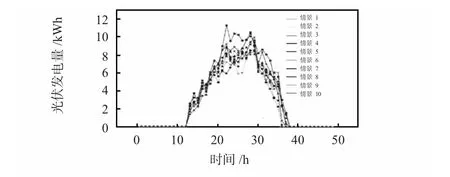
图1 光伏发电量的情景集Fig 1 Scenarios of photovoltaic power

3 微电网随机优化调度模型

实现微电网的经济调度和优化运行是微电网能量管理的主要目标。这里所述微电网系统釆用并网运行方式为本地用户供电，微电网内包含光伏发电单元、微型燃气轮机、储能及负荷，微电网可以与主网进行双向的能量交换，如图2所示。在考虑光伏发电不确定性的情况下，综合考量微型燃气轮机发电、储能设备充放电和从大电网购电的经济性，建立了并网运行模式下微电网的能量管理随机优化调度模型。

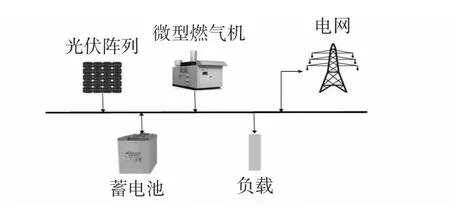
图2 微电网并网运行结构图Fig 2 On-grid micro-grid system

3.1 随机优化调度模型

微电网优化调度的目标是在满足各个分布式单元运行约束和负荷需求的限制下，实现系统运行成本最低。同时，考虑光伏发电的不确定性，结合上节所述的情景生成技术，对微电网能量优化调度建立随机期望值模型，其目标函数可以表示为

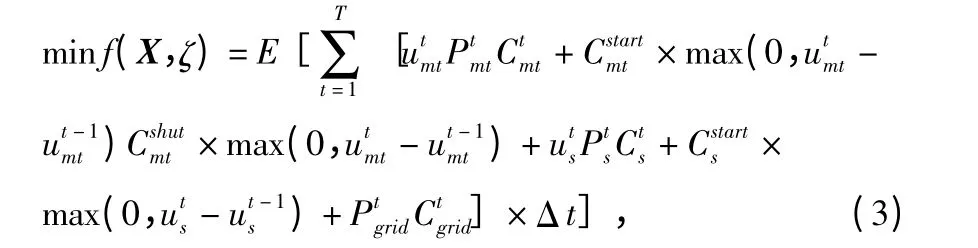
式中 f(X，ζ)为微电网运行总费用的目标函数;X 为决策变量为随机变量为t 时段微型燃气轮机的输出功率;为t 时段储能装置的充/放电功率;为t 时段微电网与大电网的交换功率;为微型燃气轮机的单位发电成本;为微型燃气轮机的启动成本;为微型燃气轮机的停机成本为储能设备的折旧成本;为储能设备的启动成本;为储能设备的停机成本;为t 时段电网电价;u 为设备运行状态，u∈{-1，0，1}。

由上式可知，微电网系统的运行总费用主要包括微型燃气轮机的发电成本、启停成本、储能设备的折旧成本以及微电网从大电网的购电成本。由于微电网可以与主网进行双向的能量交换，因此，当微电网向大电网输送电能时，购电成本为负值。

根据微电网的运行状况可知，约束条件如下:

1)节点潮流约束

微电网中分布式发电单元所在节点需满足网络潮流方程约束

式中 PDGi和PLoadi分别为节点i 处发电单元注入有功功率和负荷有功功率;QDGi和QLoadi分别为节点i 处发电单元注入无功功率和负荷无功功率;Vi和Vj分别为节点i 和节点j的电压幅值;Gij和Bij分别为节点i 和节点j 之间的电导和电纳;δij为节点i 和节点j 之间电压的相角差;Ni为与节点相连接的节点集合;Nbus为配电系统节点总数。

2)功率平衡约束

在任意调度时段内，都必须满足微电网内部电功率平衡约束

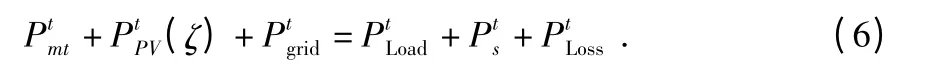
3)旋转备用约束

微电网稳定运行时，还需具备一定的旋转备用

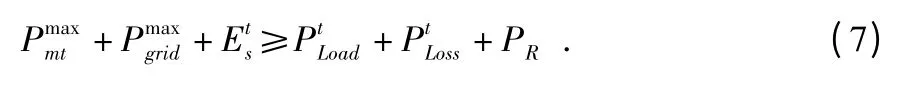
4)微型燃气轮机出力约束

微电网中微型燃气轮机收到技术条件限制，需要满足其自身的发电出力约束;同时，在任意时段要满足其相应的爬坡率约束。发电出力约束和爬坡率约束可以分布表示为

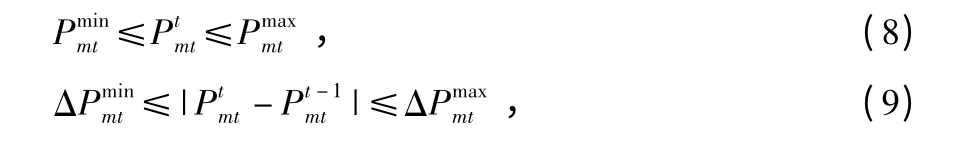
5)储能装置运行约束

充放电功率约束

储能装置容量约束

能量平衡约束

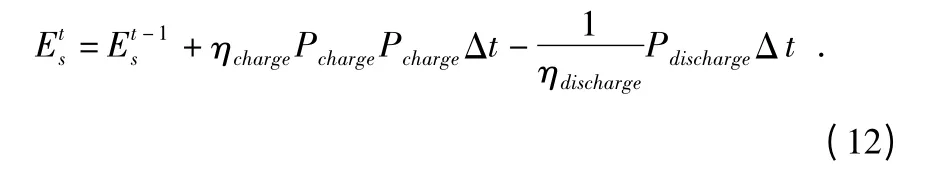
6)与大电网交互容量约束

当微电网处于并网运行时，其与大电网电能交互的最大容量不能超过联络线的物理传输容量限值或它们所达成的供求协议

3.2 模型求解

3.2.1 粒子群优化算法的基本原理假设在一个D 维的搜索空间中，由n 个粒子组成的种群X=［X1，X2，…，Xn］，其中第i 个粒子表示为一个D 维的向量Xi=［xi1，xi2，…，xiD］T，代表第i 个粒子在D 维搜索空间中的位置，亦代表问题的一个潜在解。根据目标函数即可计算出每个粒子Xi对应的适应度值。第i 个粒子的速度为Vi=［Vi1，Vi2，…，Cin］T，其个体极值为Pi=［Pi1，Pi2，…，PiD］T，种群的全局极值为Pg=［Pg1，Pg2，…，PgD］T。

在每一次迭代过程中，粒子通过个体极值和全局极值更新自身的速度和位置，更新公式如下

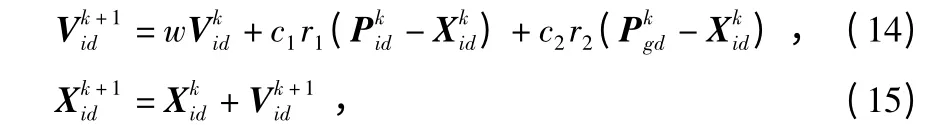
式中 w 为惯性权重;d=1，2，…，D;i=1，2，…，n;k 为当前迭代次数;Vid为粒子的速度;c1和c2为非负的常数，称为加速度因子;r1和r2为分布于［0，1］之间的随机数。为防止粒子的盲目搜索，一般建议将其位置和速度限制在一定的区间［-Xmax，Xmax］，［-Vmax，Vmax］。

3.2.2 算法的具体实现

本文釆用粒子群优化算法对微电网能量管理优化调度问题进行分析计算，则此问题转换为应用改进粒子群算法求解式(3)在式(4)～式(13)等约束条件之下的最小值问题。因此，在计算之前需要对各个约束条件进行处理，将多目标优化问题转化为单目标优化问题。本文中微电网能量优化调度的粒子群优化算法流程如图3 所示。

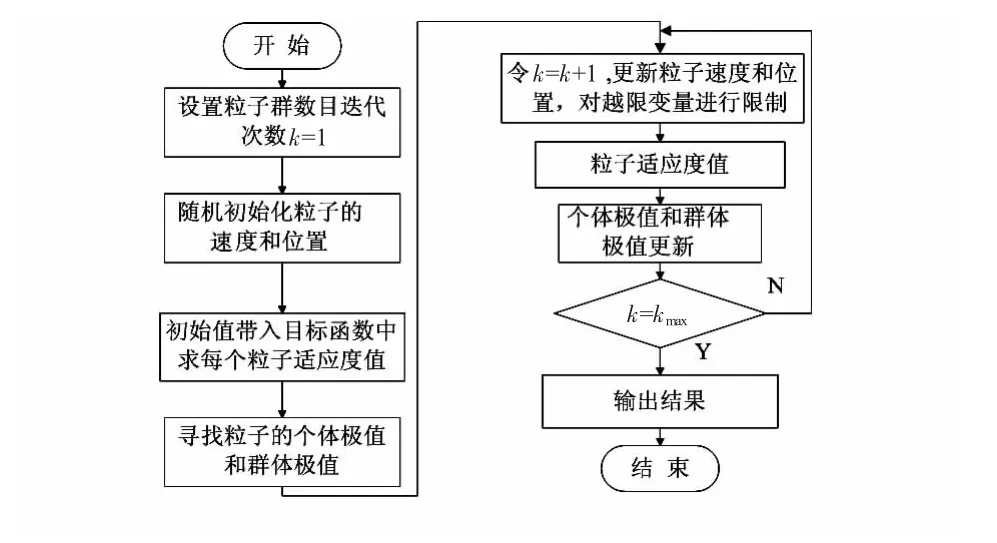
图3 微电网能量优化调度的粒子群优化算法流程Fig 3 Flowchart of particle swarm optimization algorithm for micro-grid energy optimization scheduling

3.3 仿真结果分析

为验证本文提出的模型和方法，采用图3 所述的微电网结构为研究对象。在充分考虑微电网内各个分布式单元运行约束、电网电能交互等情况基础上，有效实现微电网能量管理的优化调度和系统经济、安全与可靠运行。

本文所用的粒子群算法的参数设置如下:粒子数m=200，最大迭代次数Gmax=200，w=1，c1=1.5，c2=2.5。

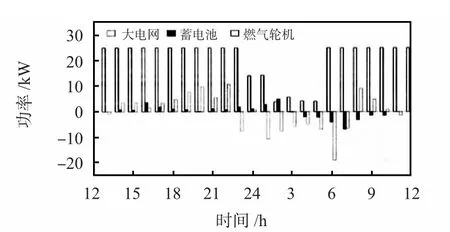
图4 基于随机模型优化得到的微电网调度方案Fig 4 Optimal power production schedule based on stochastic method

如图4 黑空色柱状图所示，微型燃气轮机在12～23 h、次日6～12 h 内运行，而在23 h 到次日7 h 时间段内停止运行。是因为微型燃气轮机的发电成本为0.68 元/kWh，而从电网的购电成本在23h 到次日7h 时间段内为0.43 元/kWh，因此，微电网从电网购电来满足微电网内的负荷更节省成本，其他时间段的购电成本较高，因此，微型燃气轮机满功率发电。在12～17 h 时间段内，蓄电池将多余的电能存储起来;从17 h 开始，购电价格上涨，且微电网内的负荷需求也开始增加，为了填补负荷缺口，蓄电池开始放电。可见，蓄电池的充放电安排跟随负荷水平与购电价格的变化而变化，在负荷波谷，购电价格低的时间段存储电量，然后在负荷波峰、购电价格高的时候输出电能，因此，可有效降低微电网的运行成本。

4 结 论

本文提出了基于光伏不确定性的微电网随机规划调度模型。其中光伏不确定性通过Monte Carlo 生成随机情景，并通过情景消减算法找到10 个情景和对应的概率。利用这些随机情景进行随机规划调度模型验证分析。仿真结果显示:随机规划调度模型具有鲁棒性，能够在可能发生的不同情节中找到折中，从而最小化微电网运行成本的期望值。因此，随机规划调度模型能够很好地用于具有不确定性的微电网能源调度。

［1］ Kriett P O，Salani M.Optimal control of a residential microgrid［J］.Energy，2012，42(1):321-330.

［2］ Chakraborty S，Weiss M D，Simoes M G.Distributed intelligent energy management system for a single-phase high-frequency AC microgrid［J］.IEEE Transactions on Industrial Electronics，2007，54(1):97-109.

［3］ Chen C，Duan S，Cai T.Smart energy management system for optimal microgrid economic operation［J］.IET Renewable Power Generation，2011，5(3):258-267.

［4］ Ahn S J，Nam S R，Choi J H.Power scheduling of distributed generators for economic and stable operation of a microgrid［J］.IEEE Transactions on Smart Grid，2013，1(4):398-405.

［5］ Tsikalakis A G，Hatziargyriou N D.Centralized control for optimizing microgrids operation［C］∥Power and Energy Society General Meeting，IEEE，2011:1-8.

［6］ Mohammadi S，Soleymani S，Mozafari B.Scenario-based stochastic operation management of microgrid including wind，photovoltaic，micro-turbine，fuel cell and energy storage devices［J］.International Journal of Electrical Power＆Energy Systems，2014，54:525-535.

［7］ Niknam T，Azizipanah-Abarghooee R，Narimani M R.An efficient scenario-based stochastic programming framework for multi-objective optimal micro-grid operation［J］.Applied Energy，2012，99:455-470.

［8］ Piperagkas G S，Anastasiadis A G，Hatziargyriou N D.Stochastic PSO-based heat and power dispatch under environmental constraints incorporating CHP and wind power units［J］.Electric Power Systems Research，2011，81(1):209-218.

［9］ Su W，Wang J.Stochastic energy scheduling in microgrids with intermittent renewable energy resources［J］.IEEE Transactions on Smart Grid，2013，99:1-9.

［10］Wu Z，Gu W，Wang R.Economic optimal schedule of CHP microgrid system using chance constrained programming and particle swarm optimization［C］∥2011 IEEE，Power and Energy Society General Meeting，San Diego，2011:1-11.

［11］樊嫣然.基于随机规划含风电场的最优经济调度［D］.南宁:广西大学，2013.