浅析多元函数Taylor公式的几个应用

殷建峰

（苏州经贸职业技术学院， 江苏 苏州 215009）

一、多元函数Taylor公式的引入

为了引入多元函数的Taylor公式，先介绍一种常见的单变量函数的Taylor公式。

定理1[1]若函数f（x）在[a，b]上有直到n阶连续导数，在（a，b）上（n+1）阶导数存在，则∀x，x0∈[a，b]，有

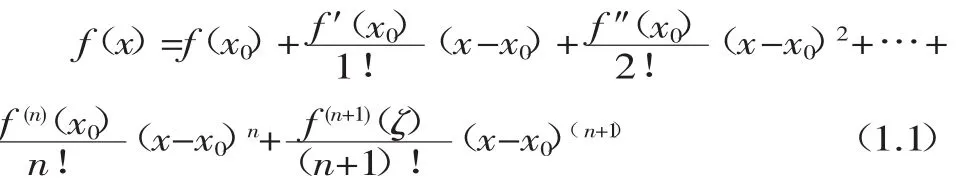
其中 ζ介于 x 与 x0之间：ζ=x0+θ（x-x0），0＜θ＜1。

（1.1）式称为函数f（x）的Taylor公式，右端多项式称为（fx）的泰勒多项式。而剩余部分

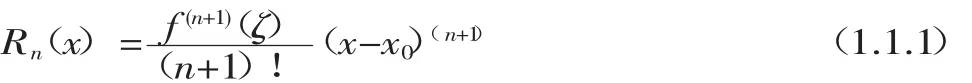
称为 f的拉格朗日（Lagrange）余项，这样（1.1）又称为带拉格朗日余项的Taylor公式，可简记为f

如果条件减弱为：函数f（x）在（a，b）内具有直到n阶导数，则余项Rn（x）可以写为Rn（x）=ο（（x-x0）n），其中（x-x0）→0，称为佩亚诺（Peano）余项，则f（x）称为带有佩亚诺余项的Taylor公式。

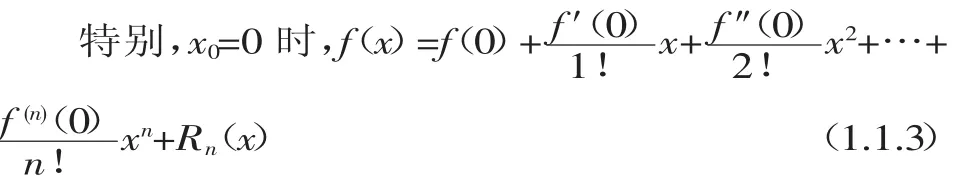
此时（1.1.3）式称为麦克劳林(Maclaurin)公式，根据Rn（x）的不同，麦克劳林公式又分带有Lagrange余项的麦克劳林公式和带有Peano余项的麦克劳林公式。

二元函数的Taylor公式，其方法是：作一个辅助函数，将二元函数化为一元函数，应用已知的一元函数的Taylor公式和复合函数的微分法得到二元函数的Taylor公式。

为了将二元函数f（x，y）在点Q（x0+h，y0+k）的函数值f（x0+h，y0+k）在点P（x0，y0）展成泰勒公式，作辅助函数 u（t）=f（x0+th，y0+tk），0≤t≤1，即 u（t）=f（x,y），x=x0+th，y=y0+tk，0≤t≤1。

显然有u（0）=f（x0，y0），u（1）=f（x0+h，y0+k）

于是，函数 f（x0+h，y0+k）在点 P（x0，y0）展成的Taylor公式就是一元函数u（t）在点0的Taylor公式（即Maclaurin公式）在t=1的值。

近日，由云南建投集团参与承建的柬埔寨西哈努克市昊利旅游娱乐综合体项目进展顺利，中国工人和柬埔寨工人一起操作安装，建筑工地一片繁忙。

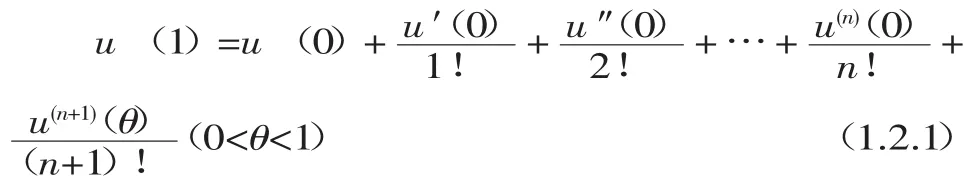
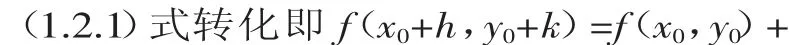
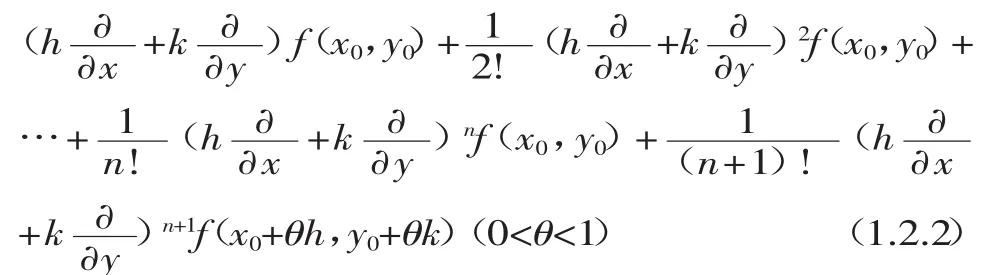
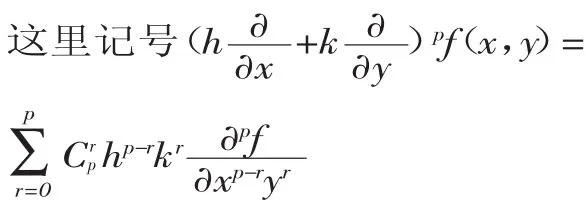
（1.2.2）式称为二元函数 f（x，y）在 P（x0，y0）的Taylor公式。

以类似的方法，可以推广出多元函数的Taylor公式（1.2）。

定理2 设D是Rn中的一个开集，a=（a1，a2，…an），h=（h1，h2，…hn），且[a，a+h]⊂D。若 f在点 a 的领域内有m+1阶偏导数，则有式（1.2）成立，式中θ∈（0，1）

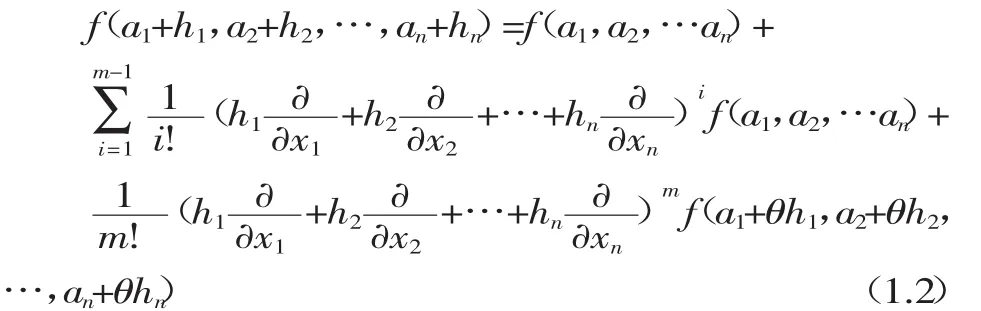
证明参见文献[2]。

二、多元函数Taylor公式的应用

多元函数Taylor公式具有广泛的用途，本文从以下几个方面举例说明。

（一）在极限方面的应用

对于特定型的极限问题，一般采用L′Hospital法则来求。但是对于一些多元的求导比较繁琐，尤其是还要多次使用L′Hospital法则的情况，此时Taylor公式往往提供了比L′Hospital法则更为有效的求极限工具。

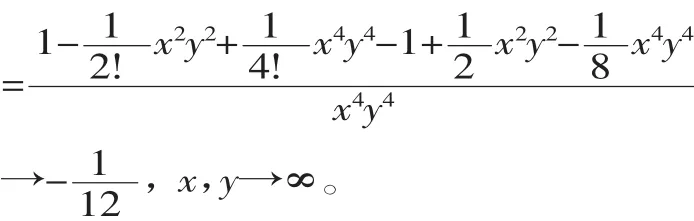
（二）在判别敛散性方面的应用

（三）在近似计算方面的应用

当要求的算式不能得出它的准确值时，即只能求出其近似值，这时Taylor公式是解决这种问题的好办法。而这一方面的应用在实际生活中比较广泛，如在工程技术方面近似计算能帮助解决棘手问题或者软件Mathematic可以分析泰勒余项的误差、知道其近似精度等等（可参考文献[3]）。

例2.3[4]求隐函数x+2y+xy+z-2ez-1+1=0在（0，0，1）点领域中的二次近似显式。

解：令z=1+a1x+b1y+c1x2+d1xy+e1y2

（四）在解析几何方面的应用

例 2.4[5]求点 p（x0，y0，z0）到平面 πAx+By+Cz+D=0的距离（其中 A2+B2+C2≠0）。

解：由Taylor定理可知：

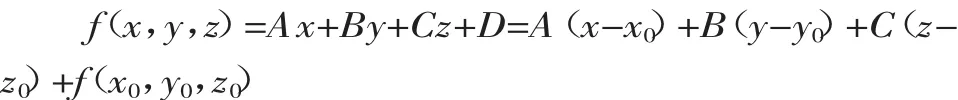
设po⊥平面π，垂足为o，点o的坐标为（x，y，z），则

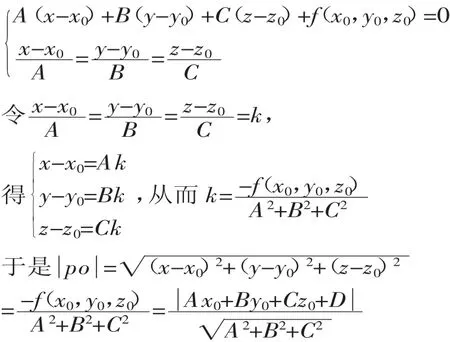
（五）在线性代数方面的应用

Taylor公式的前三项与线性代数的知识有着很紧密的联系，下面我们用向量与矩阵形式重新表达Taylor公式（2.5），并应用（2.5）式解决相关的问题。

定义1[6]在一个开区域D⊂Rn上的多元二次连续可微函数，令点带Peano余项的二阶Taylor展开式为：

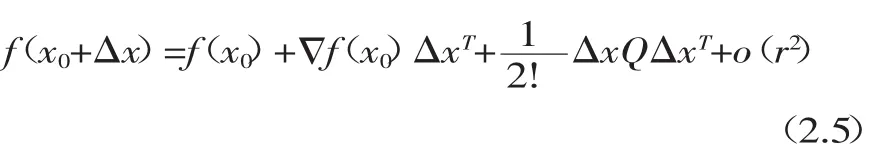
令函数的增量为Δf=f（x0+Δx）-f（x0），当Δf（x0）≠0时，可以取不同的Δx，使得Δf取到正值与负值。因此当x0是可微函数f的一个极值点时，x0必是f的驻点（又称临界点），即有

解：由于Δu（0，0，0）为零向量，故不能应用梯度方向是函数增长最快的方向性质求解。则考虑沿某单位方向 l=（α，β，γ）函数 u 的变化 u（tα，tβ，tγ）-u（0，0，0），其中 t是参数，

令 φ（t）=u（tα，tβ，tγ），由 Taylor公式展开有

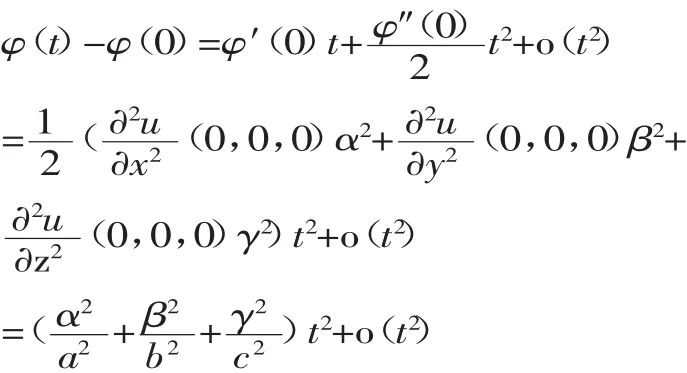
由于 a＞b＞c 及 α2+β2+γ2=1，当 t＞0 充分小时，沿方向 l=（0，0，±1）φ（t）-φ（0）最大，即函数 u 增加最快。

多元函数Taylor公式的应用远不止这些，例如还可利用其计算极值、证明不等式等，囿于篇幅，这里不再展开说明。

［1］欧阳光中.数学分析[M].北京：高等教育出版社，2007.

［2］常庚哲，史济怀.数学分析教程[M].北京：高等教育出版社，2004.

［3］邢永丽，陈建春.泰勒级数在近似计算中的应用[J].湘潭师范学院学报（自然科学版），2004（1）：5-8.

［4］吴炳熙.多元函数泰勒公式的应用[J].工科数学，1992（4）：115-116.

［5］伊水仿.一道几何题的教学处理[J].高等数学研究，2003（1）：7，31.

［6］谢惠民，易法槐，等.数学分析习题课讲义（下）[M].北京：高等教育出版社，2005.