主分量启发式约简算法的短期负荷预测
马立新,郑晓栋,尹晶晶
(上海理工大学 电气工程系,上海200093)
0 引言
负荷预测是电力系统规划、用电、调度等部门的基础,所以对负荷的预测非常重要。但是有许多因素会影响预测的准确度,如历史负荷数据、天气情况、日类型等,而这些因素是复杂的,所以对预测造成了一定的困难。
由于使用人工神经网络(ANN)算法能获得较高的预测准确度,近年来成为国内外研究的热点[1,2]。本文将使用广义回归神经网络(GRNN)对短期负荷进行预测,GRNN 在学习速度上有更强的优势,在数据样本量较少时,也能有很好的预测效果。但GRNN 不能提取数值的特征,其结果是信息丢失,预测准确度下降。考虑到粗糙集(Rough set)是数据挖掘方法之一,因其能够直接从已知的数据中建立起决策规则,故成为了一种有效的处理方法。但基于差别矩阵属性约简算法的缺点,文献[3]、[4]采用了属性重要性的启发式约简算法,改善了约简性能。这些算法虽然能有效约简属性,但是计算比较复杂,而且传统粗糙集算法有可能得不到该属性。本文在研究粗糙集[5,6]基础上,提出了一种基于属性主分量的启发式约简算法。针对有核或者是无核的决策表,该算法可以通过计算属性在差别矩阵中出现的次数与频率进行约简。算例结果表明,新模型与标准GRNN 方法相比,获得了较高的预测准确度,进而体现了该算法的优越性。
1 粗糙集简介
粗糙集的定义:

式中:S 为带有决策的信息系统;U={x1,x2,…,xn}为论域;A=C ∪D 是属性集合,C={c1,c2,…,cm}为条件属性集合,D={d}为决策属性集合;V={V1,V2,…,Vm}是属性的值域集,其中Vi是属性Ai的值域;f:U × A→V是信息函数,为论域U 中每个条件属性C 设定一个信息值V。单个决策属性的决策表如表1 所示。其中f(xi,ci)∈uj,i,f(xi,d)∈yi,且uj,i为对象xi与条件属性ci对应的值,yi为对象xi与决策属性d 对应的值。

表1 决策表的表达形式
约简具体过程:
(1)在论域中设定条件属性和决策属性,并建立成决策表。
(2)如果决策表中的条件属性是连续变量,则使用粗糙集离散化算法将决策表离散化。
(3)对离散化的决策表进行属性约简,得到约简属性和决策规则。
2 GRNN 结构
GRNN[7]由输入层、模式层及输出层组成,其中输出层由两个求和的单元组成,如图1 所示。

图1 GRNN 结构图
其基本原理是:设Xi和Yi分别是输入变量和输出变量的观察值,对于任意X 所对应的Y 值,可以采用下述公式进行预测:

由上述公式可知,σ 是GRNN 唯一需要设置的参数:扩展系数。当σ 的值越小,网络对样本的逼近就越好,但降低泛化能力;σ 的值越大,网络对样本的逼近过程越平滑,泛化能力提高,但误差相应增大。当σ 取适合的值时,网络会覆盖所有样本的因变量,与预测点距离近的训练样本对应的因变量被加了更大的权。
3 属性主分量启发式约简算法
3.1 差别矩阵
设有决策信息系统S,f(x)是对象x 在属性a 上的值,cij表示差别矩阵M 中的第i 行及第j 列的元素,则cij定义为:

式中:i=1,2,…,n;j=1,2,…,m。
差别矩阵有如下特点:
(1)差别矩阵中所有单个属性元素组成的集合等于核属性(CORE),因为当cij={a|a∈C}是单个属性的元素时,去掉后对象xi,xj就不能被正确分类,所以属性a 在C 中是绝对必要的。
(2)元素cij的宽度越短,则说明这个元素中的属性对分类所起的作用越大[8]。
(3)某个属性在差别矩阵中的数量越多,则说明该属性在整个系统中的重要程度越高。
3.2 属性主分量启发式约简算法
根据上述差别矩阵的特点,构造出属性的分量函数。属性ai的分量函数为:

式中:
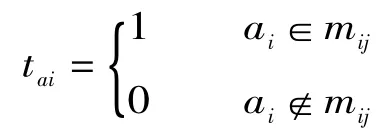
count(ai)表示属性ai出现的次数;card(mij)表示集合的基数。
分量函数综合评定了属性ai的重要程度。避免单一考虑属性出现次数多,但是元素mij宽度大,属性在元素中占据比值小,而选入约简中。也避免单一考虑属性在元素中的比值,而忽略了出现次数这种情况。分量函数值越大,该属性越重要。
使用差别矩阵提取出核属性,随后在剩下所有没有出现核属性的元素中找到分量值最大的属性纳入约简中。如果差别矩阵不能得到核属性,则直接寻找分量值最大的若干个属性作为近似约简集,这样就可以减少对原决策表的遍历搜索,使得约简算法更加简单,灵活。本文给出了属性主分量启发式算法。
输入:决策表DT=〈U,C∩D,V,f 〉。
输出:条件属性C 相对于决策属性D 的相对约简Nred。
具体步骤:
(1)求出差别矩阵M。
(2)计算决策表的相对核,即把矩阵中单个属性列入约简集合,即

(3)根据式(1)计算差别矩阵中各属性的分量值,并从合并后的差别矩阵中找到所有不包含核属性且mij≠0 的属性元素M*,即

(4)对M*中剩下的所有属性根据分量fmc(ai)函数值进行降序排列,即
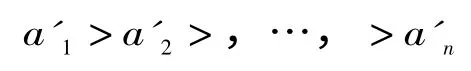
(5)在排序后的属性中选择前m 个最大分量值所对应的属性作为约简集,即

如要选取所有属性中大于75%分量值的属性,即选取前25%的属性,则设定m=25n%。因此把这m 个属性称为主分量。
算法的优点是:(1)算法在约简过程中大大减少了对原决策表的遍历搜索,约简算法更加简单,灵活;(2)分量函数所提供的启发知识无论对有核或者是无核的决策表,都能保证得到的是最小约简或次优约简;(3)算法由于不需要对差别矩阵化简,避免了传统算法中的“组合爆炸”问题。
4 算例分析
为了检验本文的方法,使用江苏某地区2012年提供的负荷数据及气象数据。因不同日类型有不同的负荷数据特征,所以把日类型分为工作日和周末两类,每类建立24 个GRNN 来预测每天的24 小时的负荷值。
选择待预测日当天的气象状况、前3 天同一时刻及前3 小时、前1 星期同一天同一时刻的历史负荷数据以及各种气象数据等。气象数据包括最高温度、最低温度、天气类型、风向、风力大小等,条件属性共计38 个。决策属性是待预测日的负荷值。
因粗糙集只能处理离散数据,所以在约简前需要将属性离散化。本文使用经典的最小信息熵离散化算法[9]。
对离散后的决策表采用主分量约简算法,并选取前25%属性的主分量后得到的约简集为L(d-1,t-1)、L(d-1,t-3)、L(d-2,t)、L(d-2,t-3)、Wd、Dd、Dd-1、Dd-2、Dd-3、Dd-7,其中:L(d,t)为待预测日t 时刻的负荷值;Wd为待预测日的天气类型;Dd为待预测日的风向。
将约简后的属性集作为输入参数,使用GRNN 算法对其进行训练并对该地区2012 年11月28 日全天的整点负荷进行预测,本文选取σ 为0.7。使用粗糙集属性约简算法的GRNN 方法(以下简称RSGRNN)与按经验选取输入属性的标准GRNN 方法的预测结果如表2 所示。其中标准GRNN 的输入属性按照经验选取为最高温度、最低温度、风力。结果的平均相对误差为

式中:R(i)、F(i)分别为负荷的实际值和预测值;N=24 为一天内的整点数。
由表2 可知,使用RSGRNN 方法与标准GRNN 方法相比能够大大提高预测的准确度,而且误差波动更小。在使用标准BP 方法对负荷进行预测时,得到平均相对误差为3.2613%,可见RSGRNN 方法远远优于标准BP 方法。
经检验,选取不同的主分量对预测的准确度有影响,如何选取最优的分量有待进一步研究。在本文算法中,采用粗糙集方法挖掘了与负荷影响较大的因素,使输入维数大幅下降,简化了神经网络的结构,并与预测负荷建立了更加密切的关系,提高了训练的效率,使网络能快速满足预测准确度,取得了较为理想的效果。

表2 预测比较结果
5 结论
本文针对以往差别矩阵约简算法问题的弱点,提出一种基于属性主分量函数的算法。该算法通过计算属性的分量函数值来确定约简集,避免了常规算法按经验选取输入参数的盲目性。通过与GRNN 结合进行仿真验证了该算法的有效性与可行性,并使所建的RSGRNN 模型具有优良稳定的预测能力。所提出的算法计算方便、灵活,并且提高了预测准确度。
[1]刘春艳,凌建春,寇林元,等.GA-BP 神经网络与BP神经网络性能比较[J].中国卫生统计,2013,30(2):173-176,181.
[2]陈耀武,汪乐宇,龙洪玉.基于组合式神经网络的短期电力负荷预测模型[J].中国电机工程学报,2001,21(4):79-82.
[3]张玲,白中英,罗守山,等.基于粗糙集和人工免疫的集成入侵检测模型[J].通信学报,2013,34(9):166-176.
[4]谢宏,程浩忠,张国立,等.基于粗糙集理论建立短期电力负荷神经网络预测模型[J].中国电机工程学报,2003,23(11):1-4.
[5]Pawlak Z.Rough set theory for intelligent industrial applications[C].Proceedings of the Second International Conference on intelligent Processing and Manufacturing of Materials,1999,1:37-44.
[6]苗夺谦,李道国.粗糙集理论、算法与应用[M].北京:清华大学出版社,2008.
[7]丁硕,常晓恒,巫庆辉,等.基于GRNN 与BPNN 的二维向量模式分类对比研究[J].国外电子测量技术,2014,33(5):56-58.
[8]胡可云.基于概念格和粗糙集的数据挖掘方法研究[D].北京:清华大学,2001.
[9]侯荣涛,史鑫明,路郁.一种基于粗糙集和信息熵理论的属性离散化算法[J].计算机应用与软件,2014,31(3):259-262.

