采用确定性测量矩阵的宽带压缩采样的研究*

王学玲,王华力,曾显华,郭克锋,孙久皓

(1.解放军理工大学 通信工程学院 江苏 南京 210007；2.辽宁沈阳铁西区65040部队 辽宁 沈阳 110005)

采用确定性测量矩阵的宽带压缩采样的研究*

王学玲1,王华力1,曾显华1,郭克锋1,孙久皓2

(1.解放军理工大学 通信工程学院 江苏 南京 210007；2.辽宁沈阳铁西区65040部队 辽宁 沈阳 110005)

在对宽带信号进行处理的过程中，常运用压缩感知的理论来获得有效的信息。而在实践压缩感知理论的压缩采样的结构中，调制宽带转换器的采样结构更加适合用于处理宽频带信号。文中研究了调制宽带转换器的压缩采样原理，也介绍了随机测量矩阵和确定性测量矩阵。分别将随机矩阵和确定性矩阵作为该调制宽带转换器的测量矩阵，对比分析了该采样结构的重构性能。研究了在确定性测量矩阵的基础上，该采样结构在折叠和非折叠条件下的信号重构性能，同时，也对系统的通道数目对性能重构和信噪比的影响进行了补充分析。

压缩采样；宽带信号；调制宽带转换器；压缩感知；测量矩阵

0 引 言

随着信息技术的高速发展，为了满足信息获取的需求，需要对宽带信号进行处理。若根据传统的Nyquist采样定理对宽带信号进行信息提取，会由于硬件的限制，很难实现。所以，需要采用新的处理方式对宽带信号进行处理。2006年，D. Donoho、E. Candes和T. Tao等人提出了压缩感知(Compressed Sensing，CS)理论[1-3]。根据此理论，在对宽带信号进行处理时，将具有有效信息的带宽先压缩，再采样，在压缩采样后的信号中再获得有效的信号。

在压缩采样的过程中，最先实现压缩采样的结构是随机采样(Random Sampling，RS)结构。其基本原理是利用采样时钟上的随机性，使得每个采样值都保持不同程度的频谱信息。随后，S. Kriolos等提出了随机解调器(Random Demodulation，RD)[4]结构。Y. C. Eldar等提出了基于稀疏多带模型的调制宽带转换器(Modulated Wideband Converter，MWC)结构。此外，目前压缩采样结构中的基于Sigma-Delta量化的模拟/信息转换器[5]、非线性仿射编解码(Nonlinear Affine Encoding/Decoding，NoLAff)结构[6]、时间编码器(Time-Encoding Machine，TEM)结构[7]等仍处在研究中。

本文首先对调制宽带转换器的压缩采样[13-14]进行了研究，并对测量矩阵的内容进行了分析介绍。突出对比了随机矩阵和确定性矩阵分别作为测量矩阵时，MWC系统的信号重构的效果。同时，在确定性矩阵作为系统测量矩阵的基础上，显著地对比分析了折叠和非折叠条件下，MWC系统的信号重构性能，也完整地研究了在非折叠条件下，MWC系统的通道数目对信号重构和信噪比的影响。其中，通过对比仿真分析，兼顾硬件实现的考虑，在确定性测量矩阵条件下，利用折叠的方式也可以达到很好的重构效果。

1 调制宽带转换器的宽带压缩采样

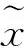
(1)

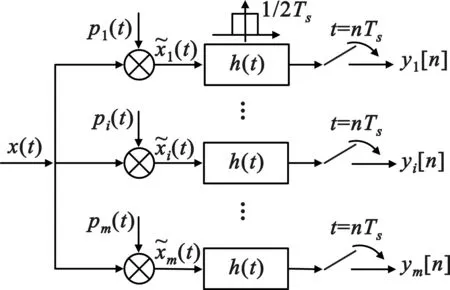
图1 调制宽带转换器的结构

MWC中，输入信号x(t)如图2中上半部分所示。子带带宽为B，子带个数为N，其中，fmax=N×B，且每个子带信号的形式可以是任意形式的信号，如AM、FM、QAM信号等。图2描述了稀疏多带信号的频谱压缩测量。稀疏多带输入信号与周期信号pi(t)的混频操作混叠了输入信号x(t)的频谱，使得所有频带的一部分能量出现在基带。此外，混频的结果是把各个频带以lfp的频率调制到低频段叠加起来，权重系数是傅立叶系数cil。

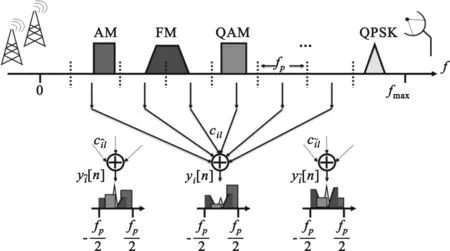
图2 稀疏多带信号的频谱压缩测量

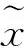
通过低通滤波器之后，信号频谱已被调制压缩到低频段，普通的ADC器件就可以实现压缩频谱信号的低速率采样，但此时ADC的采样速率必须保证对调制滤波后信号的Nyquist 采样，即fs≥fp。由于采用了低速率的ADC和便宜的RF混频器从而允许以较低成本实现宽频带信号的压缩采样。

在MWC对宽带信号进行压缩采样的过程中，测量矩阵的研究是核心内容之一。在测量矩阵的研究中，确定性测量矩阵和随机测量矩阵的研究具有重要的研究价值。

2 测量矩阵

在调制宽带转换器系统的性能重构仿真中，作为测量矩阵的调制序列的选择极为关键。目前，常用的测量矩阵大致可以分成随机测量矩阵和确定性测量矩阵两大类。随机测量矩阵包括高斯随机测量矩阵、伯努利随机测量矩阵、部分正交测量矩阵、稀疏随机测量矩阵等。随机测量矩阵的共同特点是测量矩阵中的元素相互独立且服从同一随机分布。

本文提出了一个单层神经网络模型用于求解含约束的l1-范数问题。与已有求解问题(1)的神经网络模型相比,提出的模型需要神经元数少且层数少。利用Lyapunov函数,证明了该模型的Lyapunov稳定性和渐近稳定性。数值试验结果表明,提出的模型具有良好性能且可以用于图像恢复问题。

然而，随机测量矩阵中的各个元素的产生具有随机性，因而在产生随机测量矩阵的过程中需要较大的存储空间和较高的计算量。所以，在实际的压缩采样电路中，并不常使用随机测量矩阵。

目前，压缩采样处理过程中采用的测量矩阵大多数为随机测量矩阵，而随机测量矩阵通常具有一定的随机性，并且在硬件实现上具有一定的困难。在压缩采样处理过程中采用的测量矩阵大多并不是任意随机的，而是确定的随机矩阵，这类矩阵既具有随机矩阵的一些特性，如性能不稳定，也包含了确定性测量矩阵的确定性。确定性测量矩阵是根据某一特定信号而构造的，例如，循环测量矩阵是由m序列构成的矩阵。相对于随机测量矩阵，确定性测量矩阵的最大优点是测量矩阵的确定性和稳定性。其缺点在于重构效果没有随机测量矩阵好，且所需要的最小测量维度较多。

确定性测量矩阵主要包括Toeplitz矩阵、循环测量矩阵、多项式确定性矩阵、二值稀疏矩阵等。常用的确定性测量矩阵为Toeplitz矩阵和循环测量矩阵，其构造方式为：首先生成一个向量：

u=(u1,u2,…,uN)∈RN

(2)

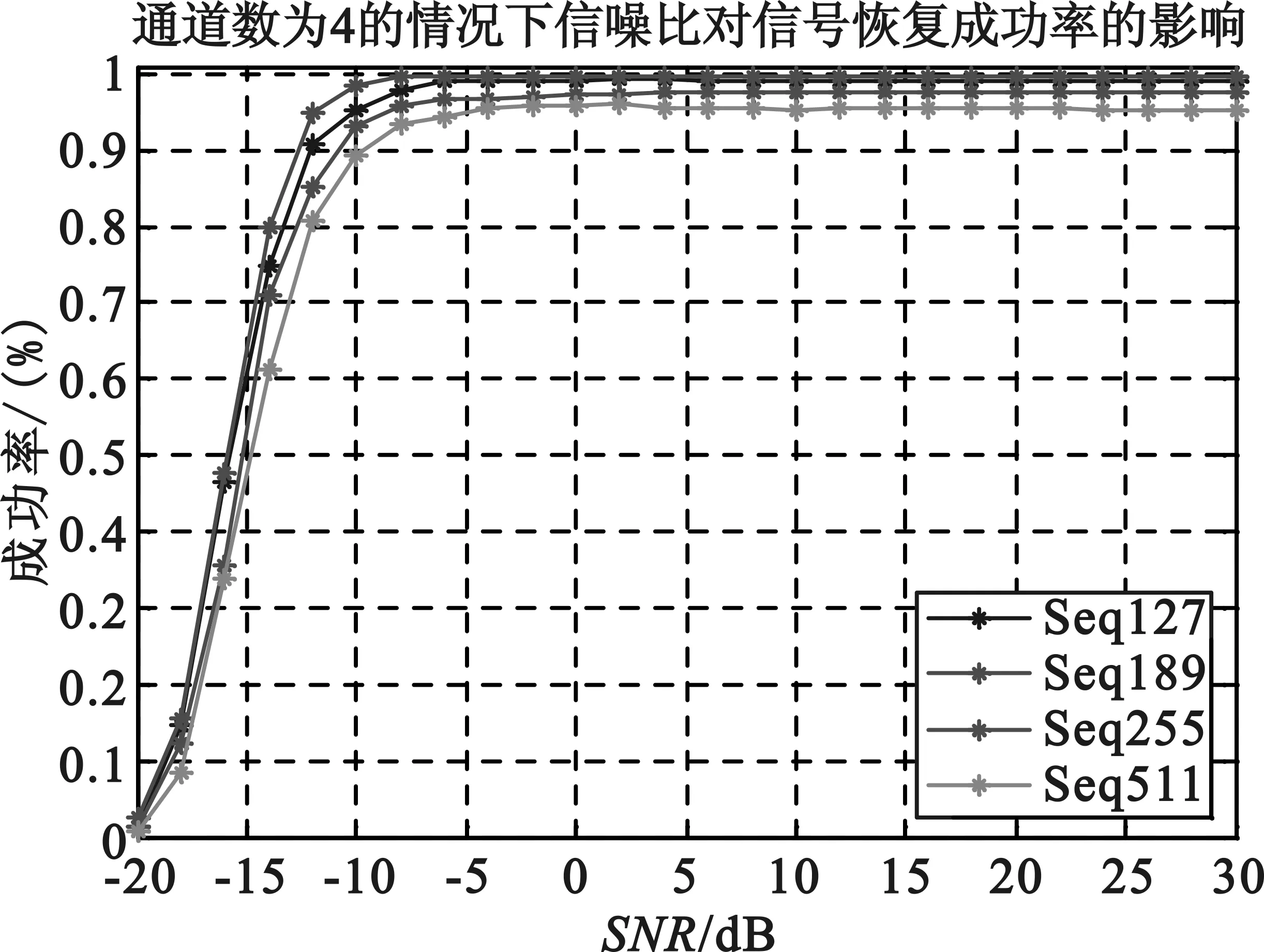
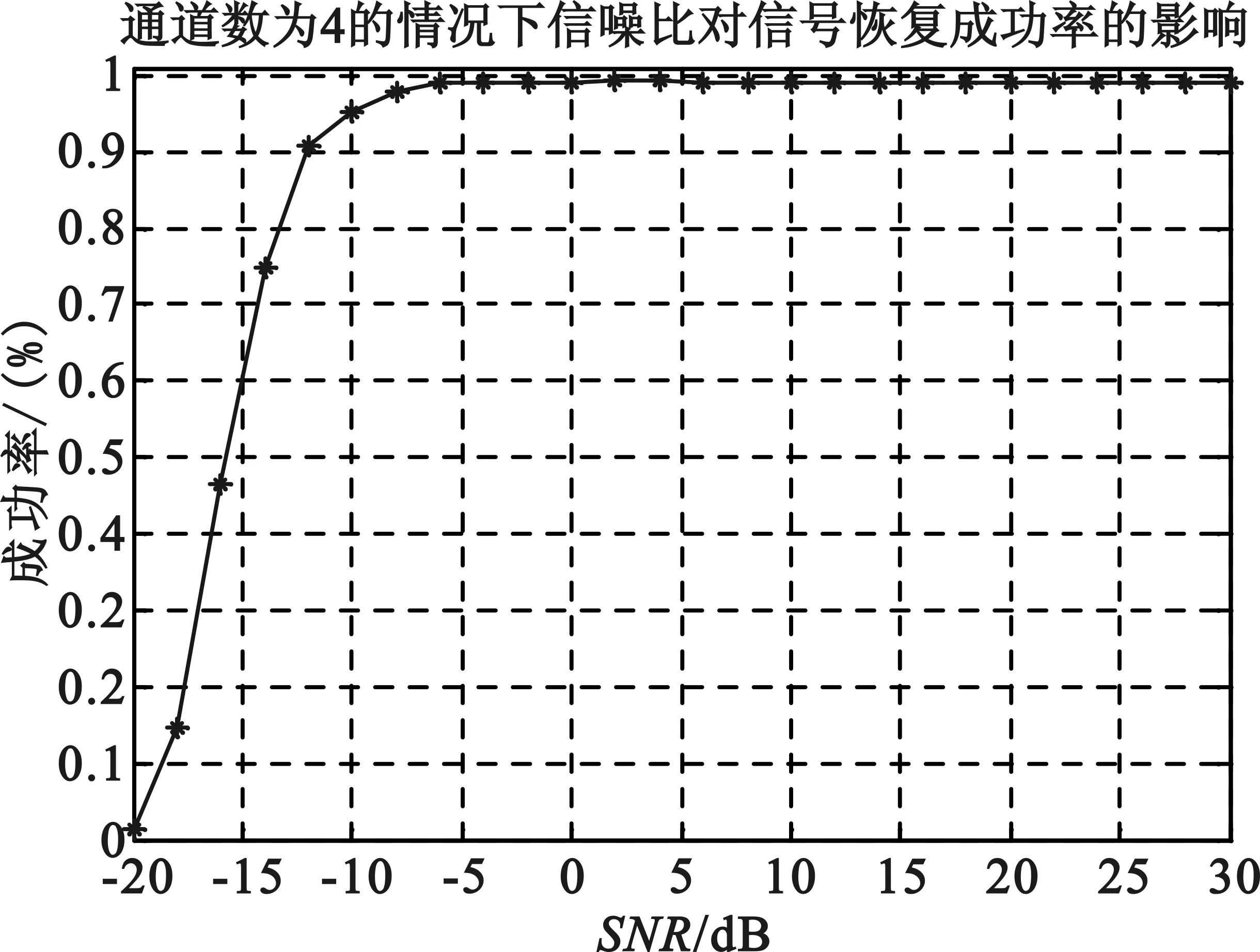
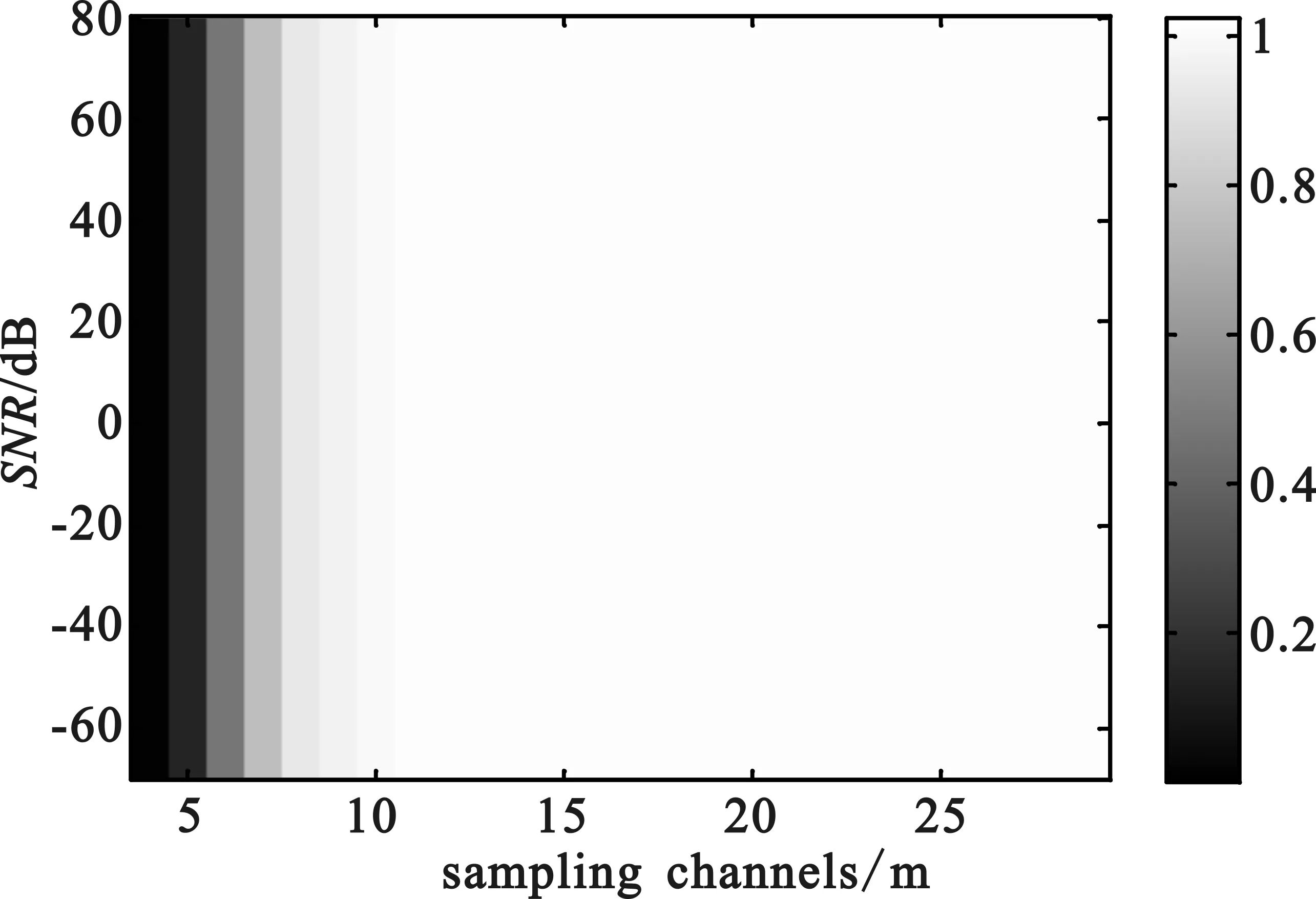
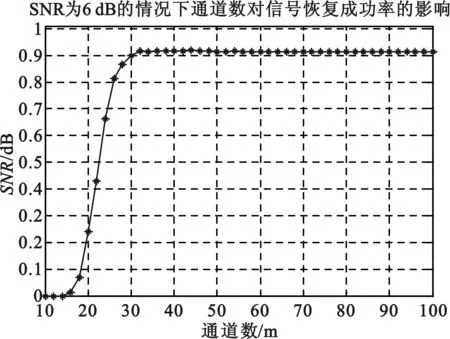
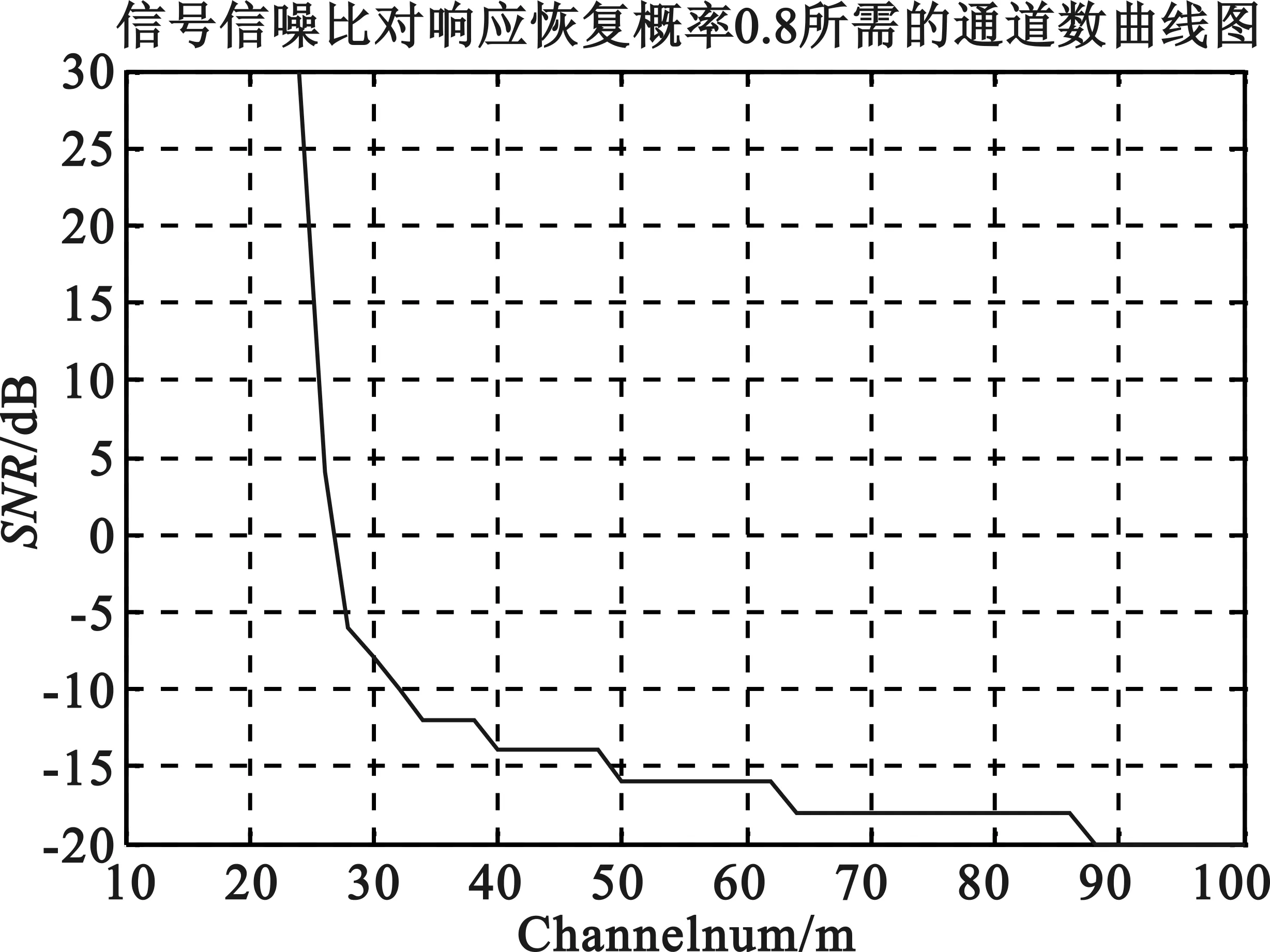
由向量u通过M(M

Toeplitz测量矩阵和循环测量矩阵通过采用行向量的循环移位的方式生成矩阵中所有的元素。也正是因为这种循环移位产生序列的方式便于硬件的实现，使得Toeplitz矩阵和循环测量矩阵能够被广泛地研究和应用。

3 性能仿真

MWC系统性能的仿真过程中，调制序列的选择至关重要。MWC系统仿真参数分别为：折叠系数q=11，奈奎斯特采样速率fnyq=480 MHz，输入宽频带信号的子带个数N=12，子带宽度B=0.8 MHz，系统通道数目m=4。其中，序列seq127，seq255，seq511采用循环测量矩阵，而序列seq189则采用伯努利随机测量矩阵。MWC采用随机测量矩阵与确定性测量矩阵的性能重构仿真如图3所示。

图3 MWC重构性能的仿真

从仿真结果中可知：在4个系统采样通道条件下，要达到90%的精确重构概率，调制序列分别为seq127，seq189，seq255，seq511的信号时，信噪比至少要分别达到-12 dB，-12 dB，-10 dB，-8 dB。同时，采用确定性测量矩阵的MWC系统的重构性能非常接近于随机测量矩阵的重构性能，考虑硬件实现方面的因素，在实践中可以考虑采用确定性测量矩阵代替随机测量矩阵。

MWC系统在采用确定性测量矩阵时，在折叠系数q=11和非折叠条件下的性能重构仿真如图4所示。

(a)折叠条件下的MWC性能重构仿真

(b)非折叠条件下的MWC性能重构仿真

图4(a)为折叠条件下的MWC性能重构仿真，图4(b)为非折叠条件下的MWC性能重构仿真。折叠条件下，当信号恢复概率达到90%时，所需信噪比至少要大于-12 dB；非折叠条件下，当MWC系统通道数目为40时，信噪比对信号恢复成功率的影响表明，在信噪比达到-12 dB以上时，信号恢复概率为90%以上。由此表明，MWC系统在折叠和非折叠的条件下，性能重构效果达到90%以上时，所需的信噪比均为-12 dB。

MWC系统在折叠和非折叠条件下的采样通道数目与信噪比的关系如图5所示。

(a)折叠条件下采样通道数目与信噪比的关系

(b)非折叠条件下采样通道数目与信噪比的关系

图5(a)为折叠条件下采样通道数目与信噪比的关系图，图5(b)为非折叠条件下采样通道数目与信噪比的关系图。折叠条件下，当达到80%以上的重构效果时，MWC系统通道数目需要大于7，而在系统通道数目低于5的条件下，性能重构概率大约为20%；非折叠条件下的采样通道数目与信噪比的关系，大致呈负指数函数的形式，当采样通道数目小于20时，性能重构概率为20%，而在通道数目大于20，且信噪比大于-10 dB时，性能重构概率保持在80%以上。

非折叠条件下，MWC的通道数目对信号恢复成功率和信噪比的影响如图6所示。

(a)非折叠时MWC的通道数目对信号恢复成功率的影响

(b)非折叠时MWC的通道数目对信噪比的影响

图6(a)为非折叠时MWC的通道数目对信号恢复成功率的影响，图6(b)为非折叠时MWC的通道数目对信噪比的影响。非折叠条件下，当MWC系统的通道数目在30以上时，信号恢复概率可以达到90%以上；MWC性能重构仿真过程中，当信号恢复概率达到80%条件时，系统通道数目与信噪比之间的作用关系呈现负指数的形式。图6(b)表明，随着系统通道数目的增加，若达到80%的信号恢复概率，所需的信噪比逐渐降低。当信噪比低于-5 dB时，所需的通道数目至少为28。

上述的仿真结果表明，利用确定性矩阵作为测量矩阵时，系统性能的重构效果和随机矩阵作为测量矩阵时的效果相当。在采用折叠的方式对信号进行压缩采样时，系统性能的重构效果上和非折叠条件下性能重构效果非常接近。另外，在此基础上也减少了采样通道的数目，节约了存储和传输的空间资源，更加便于硬件的实现。

4 结 语

本文研究了MWC系统的压缩采样的过程，分析了常用的随机测量矩阵和确定性测量矩阵的基本构成方式，分别将随机矩阵和确定性矩阵作为MWC系统的测量矩阵，对MWC系统的信号性能重构做了对比，同时，也研究了在确定性测量矩阵的基础上，折叠与非折叠条件下，MWC系统的信号重构性能的对比，以及MWC系统的通道数目对信号重构和信噪比的影响。研究结果表明，确定性测量矩阵的重构性能非常接近于随机测量矩阵的重构性能，折叠条件下的MWC系统的重构性能也非常接近于非折叠条件下的系统的重构性能。通过仿真对比分析，兼顾硬件实现的因素，可以采用确定性的测量矩阵在折叠的方式下，对宽带信号进行处理来获取有效的信息。

[1] Mishali M,Eldar Y C. Blind Multi-Band Signal Reconstruction: Compressed Sensing for Analog Signals[J]. IEEE Trans. on Signal Processing, March 2009, 57(30):993-1009.

[2] 王蓟翔，张扬.基于矩阵分解的压缩感知算法研究[J].通信技术，2011，44(16)：138-140. WANG Ji-xiang，ZHANG Yang. Compressed Sensing Algorithm based on Matrix Decomposition[J]. Communications Technology，2011，44(16)：138-140.

[3] Mishali M,Eldar Y C,Dounaevsky O. Xampling: Analog to Digital at Sub-Nyquist Rates[J]. IET Circuits, Devices and Systems, 2011, 5:8-20.

[4] Kirolos S, Laska J,Wakin M. Analog-to-Information Conversion via Random Demodulation[C]. In Proceedings of the IEEE Dallas Circuits and Systems Workshop. Richardson, USA: IEEE, 2006:71-74.

[5] Boufounos P, Baraniuk R G. Sigma Delta Quantization for Compressive Sensing[C].Conference on Wavelets XII, 6701:70104-70104, 2007.

[6] Raz G M. Method and System for Nonlinear and Affine Signal Processing. U. S. Patent 7 173 555, 2007.

[7] Kong X, Petre P, Matic R, et al. An Analog-to Information Converter for Wideband Signals using a Time Encoding Machine[C]. In Digital Signal Processing Workshop and IEEE Signal Processing Educational Workshop, 2011:414-419.

[8] Mishali M,Eldar Y C. From Theory to Practice: Sub-Nyquist Sampling of Sparse Wideband Analog Signals[J]. IEEE Journal of Selected Topics on Signal Processing, Apr. 2010, 4:375-391.

[9] GAN Lu,WANG Hua-li. Deterministic Binary Sequences for Modulated Wideband Converter[C]. SAMPTA2013, Bremen German, 2013:264-267.

[10] ZHENG Shi-lian,YANG Xiao-niu. Wideband Spectrum Sensing in Modulated Wideband Converter based Cognitive Radio System[C]. Communications and Information Technologies (ISCIT), 2011 11th International Symposium on, 2011:114-119.

[11] 李浩. 用于压缩感知的确定性测量矩阵研究[M]. 北京：北京交通大学. 2011. LI Hao.Research of Determinate Measurement Matrix Utilized in Compressed Sensing[M]. Beijing：Beijing Jiaotong University,2001.

[12] 李小波. 基于压缩感知的测量矩阵的研究[M]. 北京：北京交通大学. 2010. LI Xiao-bo. Research of Measurement Matrix based on the Compressed Sensing[M].Beijing：Beijing Jiaotong University.2010.

[13] CHEN La-ming,JIN Jian,GU Yuan-tao. A Calibration System and Perturbation Analysis for the Modulated Wideband Converter[C]. Signal Processing (ICSP), 2010 IEEE 10th International Conference on,2010:78-81.

[14] Mishali M,Eldar Y C. Expected RIP:Conditioning of the Modulated Wideband Converter[J]. In Proc. Of IEEE Transactions on Signal Processing, 2009, 57:993-1009.

Broadband Compressive Sampling with Deterministic Measurement Matrix

WANG Xue-ling1, WANG Hua-li1, ZENG Xian-hua1, GUO Ke-feng1, SUN Jiu-hao2

(1.College of Communication Engineering, PLA University of Science and Technology, Nanjing Jiangsu 210007,China; 2.PLA Unit 65040 in Shenyang Tiexi District, Shenyang Liaoning 110005,China)

In the processing of broad signal, the theory of compressed sensing is usually used to acquire effective information. However,of among the compressive sampling structures in practicing this theory, the sampling structure for modulated wideband converter is more suitable to processing broadband signal. The compressive sampling principle of modulated wideband converter is described in this paper, random measurement matrix and determinate measurement matrix also discussed in this paper. With random matrix and deterministic matrix respectively as the measurement matrix of this structure, the reconstruction performances of these two matrixes are compared and analyzed,and based on deterministic measurement matrix, the reconstruction performances in folded and unfolded conditions technically explored. Meanwhile,the influence of channel numbers on the performance reconstruction and signal-to-noise ratio is also analyzed.

compressive sampling; broadband signal; modulated wideband converter; compressed sensing; measurement matrix

10.3969/j.issn.1002-0802.2015.10.003

2015-05-01；

2015-08-19 Received date:2015-05-01；Revised date：2015-08-19

国家自然科学基金(No.61271354)

Foundation Item:National Natural Science Foundation of China (No.61271354)

TN911

A

1002-0802(2015)10-1111-05

王学玲(1989—)，女，硕士，主要研究方向为压缩感知与信号处理技术；

王华力(1967—)，男，博士，教授，主要研究方向为信息感知与信号处理；

曾显华(1990—)，男，硕士，主要研究方向为压缩感知与信号处理技术；

郭克锋(1990—)，男，博士，主要研究方向为协同通信传输技术；

孙久皓(1988—)，男，学士，主要研究方向为一体化指挥专网。