基于数学模型的湖北大别山旅游线路设计

任全玉,周海琼

1.黄冈师范学院数理学院,湖北黄冈438000

2.黄冈师范学院商学院,湖北黄冈438000

基于数学模型的湖北大别山旅游线路设计

任全玉1,周海琼2

1.黄冈师范学院数理学院,湖北黄冈438000

2.黄冈师范学院商学院,湖北黄冈438000

旅游已经成为当今老百姓休闲放松的主要方式之一，不同的人群会根据自身情况选择适合自己的旅游线路，因此，旅游线路的选择是游客面临的首要问题。本文针对湖北省大别山旅游景区，分析了旅游资源现状及旅游线路的布局，通过调查提出了存在的问题，从而指出了对湖北省大别山旅游线路开发设计的必要性。利用线性规划数学模型方法，分别建立了带约束条件的线性规划数学模型，并通过应用数学软件求得最优结果。据此，为不同的游客设计出了符合他们要求的最优游览线路。

大别山;数学模型;旅游;线路设计

现如今人类已经进入到追求个性化消费的时代，同样，追求满足自我个性的的旅游经历也是众多旅游消费者热衷追逐的，面对这种需求，众多旅行社在同一个旅游经济区域推出了不同的旅游线路供旅游消费者选择，但由于个体的差异性，目前的旅游线路仍然不能满足不同需求的旅行者。并且大多数旅行社在推出不同旅游线路的时候更多是的考虑用户对低价格的追求，而忽略了对时间及景点数量等因素的考虑。而对于旅游消费者来说，旅游路线的选择是实现自己旅游效应最大化的决定因素。所以，笔者认为，有必要按照不同旅游行者对费用、时间、景点数量及级别等不同的需求，通过数学模型的方法得出最佳旅游线路供旅游消费者选择和参考[1]。

一般说,旅游消费者按最经济、最省时、景点最多或最舒适等原则进行旅游线路的选择。旅游消费者在选择最佳旅游线路时，通常根据自己的经济状况，时间状况、身体状况及个人对景区资源偏好等综合考虑，最终选择哪一条旅游线路是旅游消费者对多个因素进行综合考虑和分析后的结果。也既是说，旅游消费者最后选定的旅游线路是旅游消费者自身的条件和偏好的体现。本文以以大别山旅游景区为例，利用数学模型的方法对旅游线路的设计进行研究。

1 湖北大别山旅游资源概况

1.1 湖北大别山4A级景区旅游资源统计分析

本文研究的湖北大别山地区包括了8个县市，分别是：团风县、红安县、麻城市、英山县、蕲春县、罗田县、大悟县和孝昌县。湖北大别山地区面积较大，旅游资源分布相对较为分散，每个县市的旅游资源分布情况不同，景区等级不同，景区的可进入性不同。因在进行旅游线路设计时仅考虑湖北大别山10个4A级旅游景区(点)作为主要分析对象,探讨本区旅游线路的选择与优化问题。

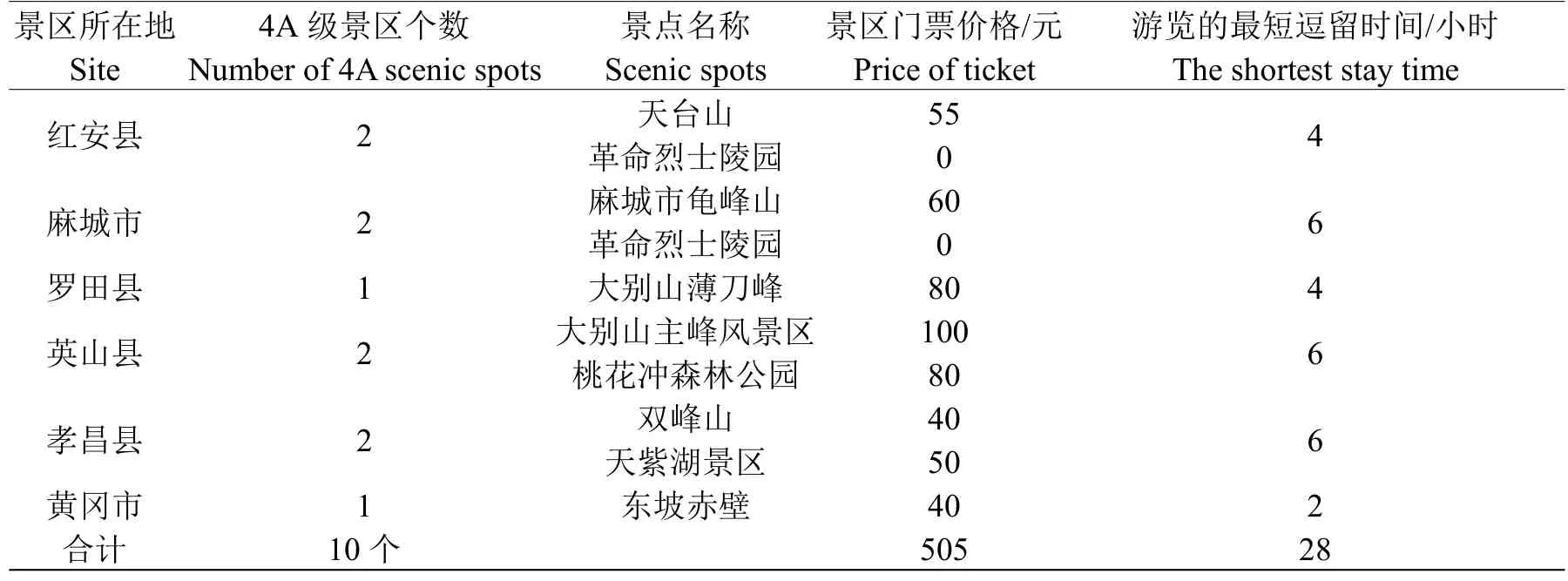
表1 湖北大别山区A级旅游景区(点)统计表Table 1 The statistics of A class scenic spots in Mountain Dabie of Hubei Province

由上表我们可以看出，湖北大别山地区各县市旅游资源相对分散、如何让旅游消费者在有效的时间游览更多的旅游景点或让旅游消费者花最少的钱旅游最多的景点等是急需解决的问题。

1.2 湖北大别山旅游线路设计现状

湖北大别山旅游资源丰富，不同的旅行社也推出了众多旅游线路供旅游消费者选择，如比较受欢迎的有黄冈旅游电子商务平台推出的湖北大别山三日游旅：黄冈赤壁公园——黄冈林家大湾——麻城龟峰山风景区——红安革命烈士陵园。黄冈神舟旅行社推出了罗田大别山三日游：罗田大别山森林公园——薄刀峰风景区——罗田天堂寨风景区。黄冈青年旅行社推出的大别山红色旅游线路是黄冈市区——罗田——红安，红色之旅三日游；“浠水三角山、灵秀山家园二日游”、“麻城龟峰山一日游”等。各旅行社推出的湖北大别山主要旅游线路如表2所示。

表2 湖北大别山主要旅游线路Table 2 Principal tourism routs in Mountain Dabie of Hubei Province

1.3 湖北大别山目前旅游线路存在的问题

通过上述旅行社推出的线路我们可以看出目前湖北大别山旅游线路设计还存在一定的不足，一是旅游线路同质化，从表2我们看到随机抽取的这些旅行社的官网是推出的旅游线路大多类似。如罗田薄刀锋、麻城龟峰山、红安烈士陵园一日游等旅游线路等基本上每家旅行社都有。二是缺乏对经济、时间、景点、满意度等不同需求的旅游线路，如黄冈市地接一日游，红安——罗田两日游，黄冈——红安——麻城三日游，这些线路的选择基本是都是只考虑的时间是一日、二日还是三日，而没有对相同旅游的不同费用，不同景点数量进行分类[2]。

针对上述分析我们可以看到，湖北大别山旅游线路还存在诸多问题，当然，要全面解决这些问题需要政府、旅游景区、旅游公司、旅行社及旅游消费者多方共同努力。现在，我们可以尝试对第四个问题即综合考虑经济、时间、景点、满意度这几大因素通过数学模型的方法为提供用户更满意的旅游线路进行分析。

2 关于旅游消费者旅行线路的模型

2.1 模型假设和符合说明

2.1.1 问题提出假设旅游消费者进行湖北大别山旅游，他们的要求分别是：不限时间，所花费用最少；费用不限，花费时间最少；限定费用，时间不限，尽可能多游览较多的旅游景点；限定时间，不限费用，尽可能多游览景点。根据这四种需求分别为游客设计出最优的旅游线路[3]。

2.1.2 旅行中的必要假设假设各个旅游景点之间的车票可预订到。天气情况在旅行期间都比较良好，没有阴雨天或其他天气的干扰，各个景点间的交通比较通畅，没有堵车等其他情况干扰；在晚上八点至第二天凌晨七点之间，如果在某地景点所在地停留超过6 h，我们必须在此地住宿，假设住宿费的用不超过250元/d，吃饭等其它费用80元/d；景点的开放时间为早八点至晚上六点之间。模型建立时会用到一些字母符号，下面需要对字母的含义进行说明(表3)[4]。

表3 模型中涉及字母含义说明Table 3 The description for letters in the model

2.2 模型的建立与求解

在此我们根据游客的不同需求建立数学模型，并进行求解。

2.2.1 不限定时间不限，花费费用最少在一般的旅游过程中，旅游费用一般包括：交通费、门票费、住宿费和餐费及其他费用这5部分构成，一般情况下，景区门票费、餐费及其他费用是确定好的，因此,在模型中可以把他们看作是常量。这样在将要建立的模型中只需要考虑在游客游览完成十个景点的前提下，使游客在游览过程中所产生的交通费和必要的住宿费达到最少就是所建模型中的最优目标。通过旅游网站上提供的信息我们可以得到如下数据：湖北大别山4A级景区的门票费用合计505元，交通所需费用大约为120元。

这时这个问题就是非常典型的旅行商问题即TSP问题。我们将在模型中把游客将产生的旅游费用最少作为我们建立模型的目标。因此，我们建立的数学模型是一个单目标化的数学模型。为了使得解决问题方便，我们引入两个0～1变量，如果我们要游览某个景区或者在某地住宿，此变量为1，否则此变量取值为0。此时我们可以构造出游客旅游过程中产生总费用目标函数的表达式，并且给出此模型相应的约束条件。目标函数：

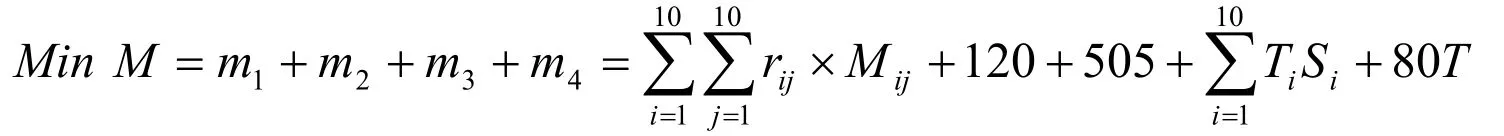
其中m1表示交通费用，m2表示门票费用，m3表示住宿费用，m4表示吃饭等其他费用，T表示游览的总天数，这个目标函数的约束条件为：

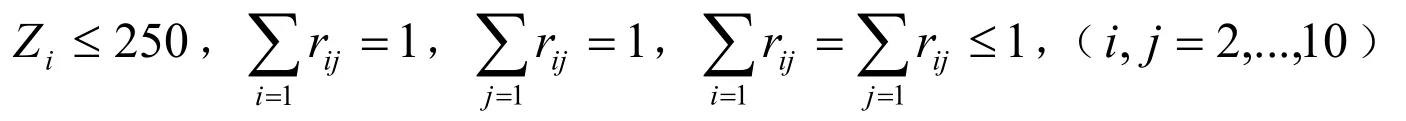
我们根据这个模型，应用数学软件LINGO编程进行求解得到：不限定时间，花费费用最小的旅游线路如下：黄冈东坡赤壁——黄冈遗爱湖公园——林家大湾——罗田薄刀峰风景区——罗田大别山国家级森林公园（住宿罗田）——麻城龟山——麻城烈士陵园（住宿—麻城）——浠水三角山——黄梅五祖寺、四祖寺，确定总费用为890元。

2.2.2 费用不限，花费时间最少在这种情况下，游客在旅游的时间由在交通上花费的时间、游客在景点停留的时间以及必要的夜晚住宿的时间三部分组成。考虑到出行的安全问题，我们一般从一个景点到达另一个景点的交通时间是固定的，这时想达到花费时间最少这一目的我们因该尽量使我们在景点停留的时间和住宿时间达到最少即可。通过互联网我们可以收集到各个景点的交通情况，并根据正常行驶车速估计，各个车站与景点间的交通总时间为：t2=10 h，在上一个模型的基础上，把数学模型的目标改为要求时间最少，同时调整模型的约束条件。模型建立如下。目标函数为：

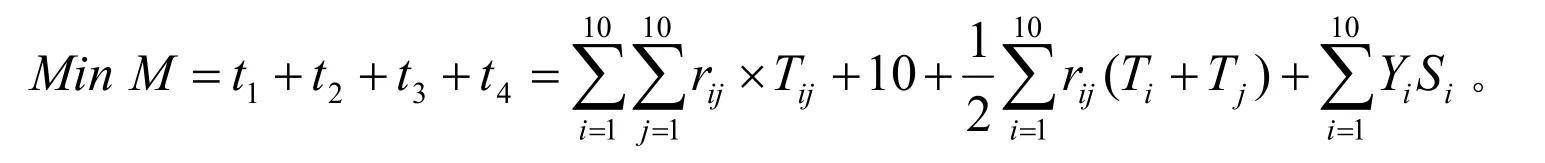
其中，t1表示景点间交通所需要的时间，t3表示在各个景点停留时间，t4表示住宿时间，此时的约束条件为：

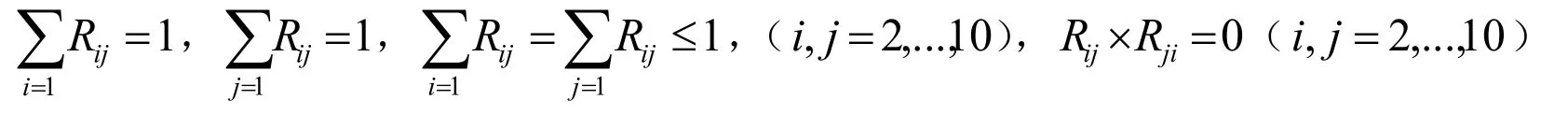
应用数学软件LINGO编程进行求解得到：如果费用不限，花费最短时间为2 d，这时的最佳旅游线路为：黄冈——英山桃花冲——英山大别山主峰（住宿英山）——罗田薄刀峰——罗田天堂寨。

2.2.3 限定费用，时间不限，尽可能多游览景点限定旅游费用，尽可能多游览景点。在这里我们同样也使用单目标优化的数学模型，把游览的景点数目最多作为我们的目标，同样还是以第一个模型为基础，我们再加上总费用小于1000元的约束条件，建立数学模型如下。目标函数为：MaxN，此时的约束条件为：在第一个模型的约束基础上加上总费用约束，m≤1000元。然后应用数学软件编程求解，得到在限定费用1000，时间不限的前提下最多旅游的景点数为7个景点，所花费总时间为3天。我们推荐的最优游览路线为：黄冈遗爱湖公园〉林家大湾〉浠水三角山（住宿浠水）〉罗田大别山国家级森林公园〉罗田天堂寨风景区（住宿罗田）〉黄梅五祖寺〉黄梅四祖寺。旅游花费费用为736元左右，由于为了解题方便我们在模型求解时没有考虑一日三餐的吃饭费用80元/d这个固定的消费值，因此我们总的旅游费用应该为736+80×3=976元。这时总的旅游花费满足满足旅客的要求。

2.2.4 限定时间，不限费用，尽可能多游览景点如果旅客提出的要求是限定时间，不限制旅游过程中所产生的费用，在有限的时间内尽可能的多去一些游览景点，这时我们可以把旅游景点数作为我们建立模型的目标，同样我们在此建立一个单目标规划的数学模型，并在本文中第二个模型的基础上总时间不超3 d这样一个约束条件，我们建立数学模型如下。目标函数：MaxN，

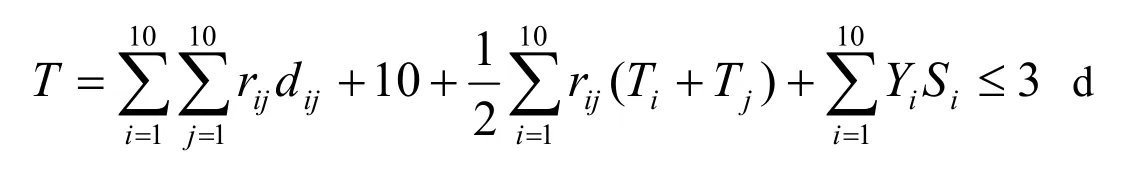
通过数学软件编程求得，在3 d内这样一个限制条件下，最多游览10个景点。我们推荐最优的旅游线路为：黄冈遗爱湖公园〉林家大湾〉黄冈东坡赤壁〉浠水三角山（住宿浠水）〉罗田大别山国家级森林公园〉罗田天堂寨风景区〉罗田薄刀锋（住宿罗田）〉麻城龟山〉麻城革命烈士陵园〉李先念纪馆、董必武纪念馆。通过旅游行程分析我们可以看到这条路线是可行的，并且可以保证在3 d内使得游客游览的景点数是最多的。

3 结束语

合理的进行旅游线路的设计是实现旅游消费者满意的第一步，为了满足不同旅游消费者的不同需求，笔者进行了合理的假设，把问题转化为数学模型的问题，运用软件进行求解，使问题得到了比较合理的解决。但是，由于没有考虑旅游过程中天气的变化及旅游行程中旅游消费的休息等因素，所以有一定的局限性。若将此作为旅游的参考，还需要综合考虑具体的实际情况再来定夺。

[1]施广伟.基于模糊数学和Dijkstra算法的地质公园地质科普旅游线路设计[D].西安:长安大学,2010

[2]叶俊.体验经济视角下黄冈市旅游线路产品的优化与设计[J].武汉:农村经济与科技,2015,26(3):157-158

[3]王佳,赵宏丽.基于Dijkstra算法的京津冀旅游交通线路优化研究[J].统计与决策:自然科学版,2011,13(7):81-83

[4]王战友,李强,黄利萍.基于数学模型的旅游线路优化设计[J].企业导报,2011,12(12):249-250

The Design and Optimization for the Tourism Route in Mountain Dabie of Hubei Province Based on the Mathematical Model

REN Quan-yu1,ZHOU Hai-qiong2
1.College of Mathematics and Physics/Huanggang Normal University,Huanggang438000,China
2.School of Business/Huanggang Normal University,Huanggang438000,China

At present,tourism is one of the main selects for a leisure of civilians and the different people may select routs to suit for themselves.Therefore it is a key to select the tourism routes when people intend to travel.This paper analyzed the tourism resources and route layouts in Mountain Dabie Scenic Area and pointed out some problems through investigation to put forward a necessity to the tourism route design for Mountain Dabie Scenic Area in Hubei Province.The linear programming mathematical models with limited conditions were established respectively by way of a linear mathematical model to obtain the optimal results with the mathematical software and accordingly to design an optimal route for a tourist.

Mountain Dabie;mathematical model;tourism;route design

F590.1

:A

:1000-2324(2015)06-0947-04

2015-03-20

:2015-05-20

2015年湖北省教育厅人文社科重点项目:基于模糊数学及Dijkstra算法的大别山旅游线路的设计与优化(15D1182015);2015年湖北省教育厅科学研究计划项目:基于数学模型的大别山旅游线路设计与优化(B2015215)

任全玉(1976-),男,黑龙江牡丹江人,硕士,教师.主要从事经济数学的研究.E-mail:76158545@qq.com