二维Radon变换在图像重建中的重要性质及定理

李 静

(周口师范学院 数学与统计学院，河南 周口 466001)

二维Radon变换在图像重建中的重要性质及定理

李 静

(周口师范学院 数学与统计学院，河南 周口 466001)

Radon变换及其逆变换作为图像重建的数学基础，在图像重建中有着特殊的意义.首先介绍了二维Radon变换定义的几种形式，然后总结了二维Radon变换的基本性质：线性、带线性、对称性、周期性、位移性等，最后给出了中心切片定理和二维Radon逆变换公式并给予证明.

Radon变换；逆变换；傅里叶变换；图像重构；卷积

0 引言

Radon变换(或称经典Radon变换)是由奥地利数学家Radon于1917年提出来的.它作为积分几何学的基石，为一大类图像重构(层析成像)问题提供了一个统一的数学基础，已被广泛应用于医学、分子生物、无损探测、地球物理、材料科学、天文等方面.迄今为止，人们已经开发出基于Radon变换的多种比较成熟的重建算法.

1 Radon变换的定义

一个n维函数f(x1,x2,…,xn)的Radon变换定义为n-1维超平面上的积分值.当n=2时，Radon变换可表示为[1]

其中直线L是oxy平面的任意一条直线，t是原点到直线L的距离，θ是直线L与x轴的夹角.Rf(t,θ)也可记作Rθf(t).

当直线L的方程为xcosθ+ysinθ=t时，Radon变换可表示为

如果借助Delta函数，Radon变换还可表示为

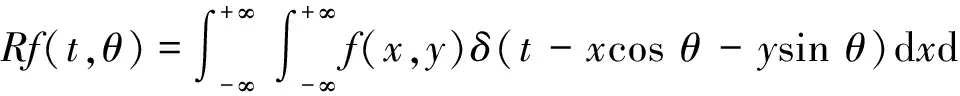
2 Radon变换的基本性质

1)线性.R[af(x,y)+bg(x,y)]=aRf(t,θ)+bRg(t,θ).

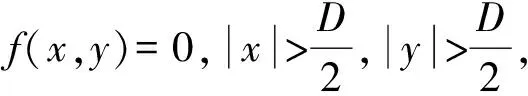
3)对称性.Rf(t,θ)=Rf(-t,θ±π).

4)周期性.Rf(t,θ)=Rf(t,θ±2kπ)，k为整数.

5)位移性.若R[f(x,y)]=Rf(t,cosθ,sinθ)，则

R[f(x-a,y-b)]=Rf(t-acosθ-bsinθ,θ).

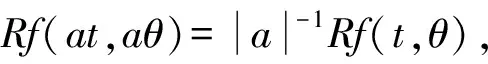
Rf(-t,-θ)=Rf(t,θ).

3 卷积

已知X=(x,y)，定义卷积如下

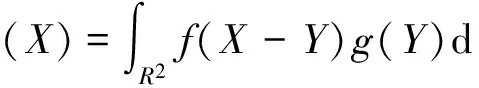
定理1 已知X=(x,y)，φ=(cosθ,sinθ)，则对于任意函数f,g∈φ(R2)(无限可微且速降)，有

Rφ(f*g)=Rφf*Rφg.

令X-Y=Z,则

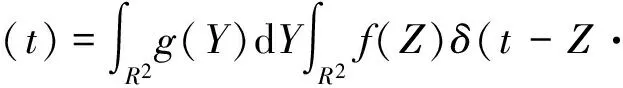
再令Y·φ=m，则

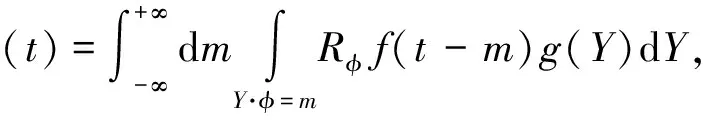
又因为

所以

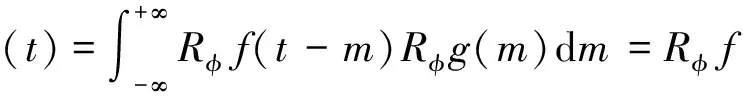
4 中心切片定理

图像重构问题实质是由投影数据如何解出成像平面上各像素点的衰减系数的问题.由投影重建图像的重要依据是傅里叶切片定理，或称投影定理、中心切片定理.该定理指出[3]：某图像函数f(x,y)在某一方向上的投影函数Rf(t,β)=Rfβ(t)的关于t的一维傅里叶变换，给出f(x,y)的二维傅里叶变换F(u,v)的一个切片，该切片与u轴相交成β角，且通过坐标原点.具体内容如下：

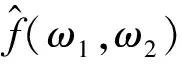
(1)

证明 由题意知

由ω1=ωcosθ，ω2=ωsinθ，即得

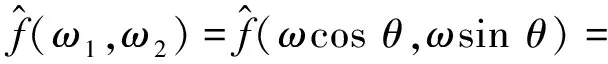
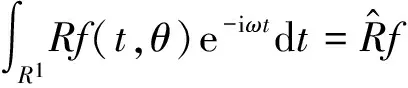
5 Radon逆变换

为推导出Radon逆变换公式，我们首先对(1)式进行傅里叶逆变换得

由中心切片定理得

进一步化为

当x,y用极坐标表示时,

Radon逆变换也可表示为[4]

(2)

其中B,Hx,Dx分别表示反投影算子、Hilbert算子和导数算子.

由(2)式可知，已知投影数据Rf(t,θ)，求其逆变换，可经过以下3个步骤：

1)Rf(t,θ)关于第一个变量t求偏导数；

2)对其偏导数做关于t的Hilbert变换；

3)对经过Hilbert变换后的函数做反投影变换和归一化运算.

6 结论

总结了Radon变换的定义的几种形式以及基本性质、卷积定理、中心切片定理及Radon逆变换公式，这些都可以推广到n维空间，为以后研究Radon变换和图像重建工作提供一定的帮助.

[1] NATTERER F. The Mathematics of Computerized Tomography[M]. New York: Wiley，1986:9-12.

[2] 张远鹏. 计算机图像处理技术基础[M].北京：北京大学出版社，1996:12-18.

[3] 庄天戈. CT原理与算法[M].上海：上海交通大学出版社，1992:30-36.

[4] 邸燕，常宏宇.Radon变换在断层成像中的应用[J].数学的实践与认识,2004，34(12):87-90.

Important Properties and Theorems of Two-dimensional Radon Transform in Image Reconstruction

LI Jing

(SchoolofMathematicsandStatistics,ZhoukouNormalUniversity,Zhoukou466001,China)

The Radon transform and its inverse transform have special significance as the mathematical foundation of the image reconstruction. First, several forms of the definition of two-dimension Radon transform are introduced, and then the basic properties of two-dimensional Radon transform are summarized: linear, linear, symmetry, periodic, displacement and so on. Finally, the center section theorem and a two-dimensional Radon inverse transform formula are given and proved.

Radon transform; inverse transform; Fourier transform; image reconstruction; convolution

2015-09-25

周口师范学院青年科研基金项目(ZKNUB315209)

李 静(1986—)，女，河南周口人，周口师范学院数学与统计学院教师.

10.3969/j.issn.1007-0834.2015.04.006

TP391

A

1007-0834(2015)04-0021-03