关于非单调拟牛顿算法的一个改进

赵建卫， 景书杰

(河南理工大学 数学与信息科学学院,河南 焦作 454000)

关于非单调拟牛顿算法的一个改进

赵建卫， 景书杰

(河南理工大学 数学与信息科学学院,河南 焦作 454000)

对于无约束优化问题提出了一类新的非单调拟牛顿算法.该算法在修正的拟牛顿方程基础上添加参数，从而推广了已有的拟牛顿方程.采用非单调线性搜索准则，并在一定条件下证明了新的非单调拟牛顿算法具有全局收敛性.

无约束优化;非单调;拟牛顿方程;线性搜索准则;全局收敛性

0 引言

1 新算法的提出

在文献[8]中，韦增欣等利用目标函数的泰勒展式提出了一种新的拟牛顿方程

(1)

其中

(2)

对(1)和(2)，引入参数m(0≤m≤1)进行加权处理，可以得到如下新算法：

(3)

2 新算法的收敛性分析

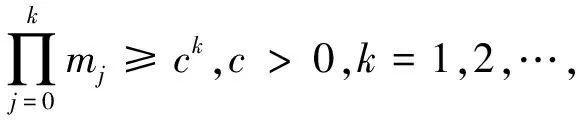
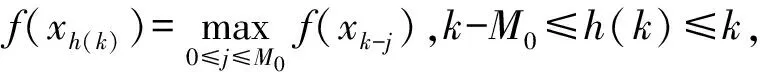
(4)

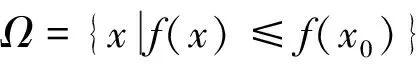
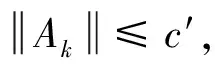
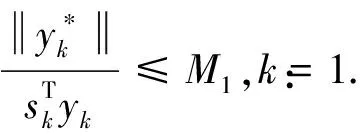
证明 先证明1).根据假设，

(5)

其中，ε=xk+θsk,ε3=xk+θ1ksk,ε4=xk+θ2ksk，θ,θ1k,θ2k∈(0,1).

(6)

再证明2).

(7)

(8)

证明 根据引理2和引理3式可得

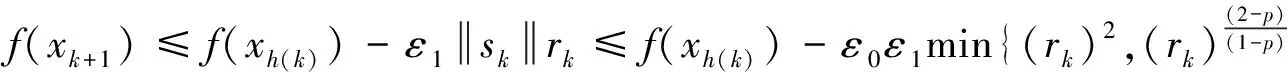
令

ρk=ε0ε1min{(rk)2,(rk)(2-p)/(1-p)}.

根据引理1可得

(9)

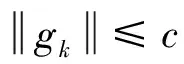
(10)

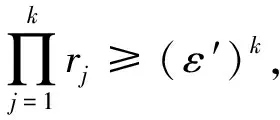
(11)

根据引理3，还可以得到

[1] 袁亚湘，孙文瑜．最优化理论与方法[M]. 北京：科学出版社，1997：183-218．

[2] 焦宝聪.一类超线性收敛的广义拟牛顿算法[J].高等学校计算数学学报,1999,21(6):178-188.

[3] 楚添定,马柏林.基于新的拟牛顿方程的Broyden-Fletcher-Goldfarb-Shanno算法[J].应用数学与计算数学学报,2012, 26(4):360-367.

[4] 刘辉.解非线性方程的牛顿迭代法及其应用[J].重庆工学院学报：自然科学版,2007,21(8):5-8.

[5] 陈兰平,焦宗聪.一般无约束优化问题的广义拟牛顿法[J].数学进展,2007, 36(1):81-85.

[6] WEI ZENGXIN, LI GUOYIN, QI LIQUN. New quasi-Newton methods for unconstrained optimization problems [J]. Applied Mathematics and Computation，2006，175(2): 1 156-1 188.

[7] XIAO WEI，SUN FENGJIAN．On quasi-Newton methods with modified quasi-Newton equation[C]//JIANG YONG，LI JIANLIANG. Proceeding of 2008 International Pre-Olympic Congress on Computer Science，Volume Ⅱ：Information Science and Engineering.Waltham: World Academic Press, 2008:359-363.

[8] 韦增欣，谢品杰，顾能柱.一类拟牛顿算法的收敛性[J].广西科学，2006,13(4)：282-287.

[9] SUN WENYU, ZHOU QUNYAN. An unconstrained method using non-monotone second order Goldstein’s line search[J]．Science in China Series A：Mathematics，2007, 6(10)：1 389-1 400.

[10] 王海滨.基于新拟牛顿方程的一类超线性收敛的改进BFGS算法[J].兰州理工大学学报,2007,33(4):150-152.

A Revised Non-monotone Quasi-Newton Algorithm

ZHAO Jianwei, JING Shujie

(CollegeofMathematicsandInformationScience,HenanPolytechnicUniversity,Jiaozuo454000,China)

For unconstrained optimization problem, a class of new non-monotone quasi-Newton algorithm is put forward. This new algorithm adds two parameters based on modified quasi-Newton equation, generalizing the existing quasi-Newton equation. Using non-monotonic linear search criteria, and under certain condition, it proves that the new non-monotone quasi-Newton algorithm has global convergence.

unconstrained optimization; non-monotone; quasi-newton equation; linear search criteria; global convergence

2015-09-07

国家自然科学基金资助项目(10671057)；河南省一级重点学科支持项目；河南理工大学校级重点学科支持项目

赵建卫(1988—)，男，河南济源人，河南理工大学数学与信息科学学院在读硕士研究生.

10.3969/j.issn.1007-0834.2015.04.004

O221

A

1007-0834(2015)04-0013-03