蛇型DGS微带滤波器的设计
王 克,陈小强
(兰州交通大学 自动化与电气工程学院,甘肃 兰州 730070)
蛇型DGS微带滤波器的设计
王 克,陈小强
(兰州交通大学 自动化与电气工程学院,甘肃 兰州 730070)
提出了一种将哑铃型DGS中的长方形缝隙变为蛇形缝隙的蛇型DGS,建立了等效电路模型并进行参数推导.基于控制变量法分析参数变化对蛇型DGS结构频率特性及等效电路参数的影响.将该结构应用于低通滤波器的设计,分别在HFSS和MATLAB环境下对设计的滤波器及其等效电路模型进行仿真,两种方法的仿真结果具有很好的一致性.结果表明,该结构可在不增加缺陷面积的情况下得到更低的衰减频率和更多的谐振频率点.
缺陷接地结构; 等效电路; 低通滤波器
0 引言
近年来,不同结构的PBG (Photonic Band Gap)光子带隙结构和DGS(Defected Ground Structure)缺陷接地结构的设计研究已经成为热点课题.和光子带隙结构(PBG)类似,缺陷接地结构(DGS)也是在金属接地平面上蚀刻出缺陷的图案.通过改变电路衬底材料有效介电常数的分布,从而改变微带线的有效电感和有效电容,使得由DGS结构构成的微带线具有慢波特性和带阻特性[1-4].和PBG结构相比较,DGS结构仅由1个缺陷单元构成,它的带隙中心频率仅由该缺陷单元结构决定,而PBG结构是由若干个缺陷单元组成的缺陷阵列,它的带隙中心频率由缺陷阵列间距、排列方式和几何结构等诸多因素决定.因此,DGS结构具有结构简单,易于电磁场理论分析和等效电路建模分析,更适于集成电路实际应用的显著优点.已广泛应用于微波和毫米波的设计中.
笔者提出蛇型DGS微带线的等效电路模型.利用HFSS和MATLAB分别对蛇型DGS单元及其等效电路模型进行仿真分析,研究蛇型DGS单元各参数变化时对其频率特性的影响.通过DGS结构的微带滤波器的设计来证明等效电路模型的正确性.
1 蛇型DGS的频率特性及等效电路
1.1 蛇型DGS的结构组成和频率特性
如图1所示, 蛇型DGS是由2个矩形和它们之间的1个蛇形缝隙组成[5-6].选取文献[1]和[7]中提出的DGS单元相同的参数,介质厚度为h=0.787 4 mm,介电常数εr=2.2, 尺寸分别是w=2.4 mm,a=b=5 mm,n=6,g=0.38 mm.利用HFSS对图1中的DGS结构进行仿真,并与文献[1]中哑铃型DGS仿真结果对比如图2所示.
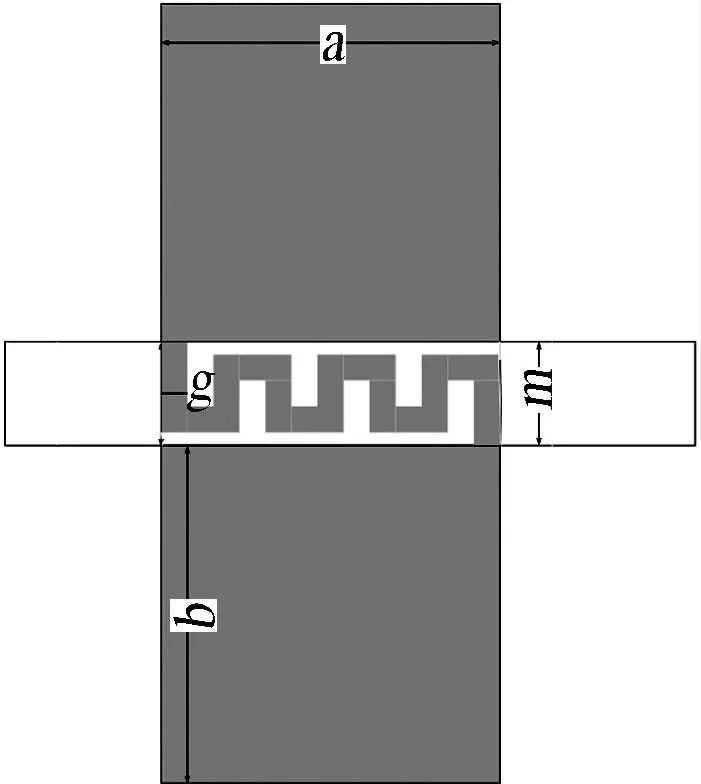
图1 蛇型DGS单元示意图Fig.1 Schematic view of snake DGS unit
对比同一软件下两种不同结构的仿真结果可知,蛇型DGS结构微带线两侧的矩形缺陷面积和形状都与哑铃型DGS结构一致,在只改变缝隙g的情况下就可使原哑铃型DGS传输线产生更低的带隙中心频率,在同样带宽范围内,产生的谐振频率点更多;蛇型DGS结构与文献[7-8]提出的螺旋型DGS结构比较,在缺陷所占的面积不变的情况下同样能产生两个谐振频率点,但设计参数减少,结构简单,易于电路的加工设计.
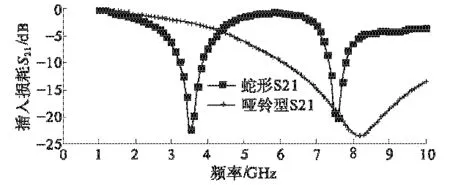
图2 蛇型DGS与哑铃型DGS单元的仿真结果Fig.2 The simulation results of snake DGS and dumbbell DGS unit
1.2 蛇型DGS结构的等效电路的模型及参数的提取
哑铃型DGS结构与LC并联电路相似,具有单极点低通滤波器的带阻特性.笔者提出的蛇型DGS单元具有两个谐振频率点.因此,利用两个LC并联电路的串联电路来等效文中蛇型DGS单元,每个谐振点由一个LC并联电路来等效.将实际微带线和介质本身的损耗及电磁波辐射等因素考虑在内,应取两个RLC串联电路来等效[9-10],如图3所示.利用式(1)、(2)计算得等效电路的参数,电阻R由式(3)得出[10].蛇型DGS单元的电磁仿真与等效电路的仿真如图4所示.

图3 蛇型DGS单元的等效电路模型Fig.3 Equivalent circuit model of snake DGS unit

图4 蛇型DGS单元电磁仿真与等效电路的仿真Fig.4 Simulation of electromagnetic and equivalent circuit of snake DGS unit.
(1)

(2)

(3)
2 蛇型DGS参数变化对频率特性的影响
由文献[2,3,5,11-13]可知,影响DGS微带线阻带特性的参数是微带线两侧矩形的长a、宽b和蛇型缝隙的宽g、U形拐点数n.下面讨论蛇型DGS参数变化对频率特性的影响.改变DGS单元的参数,然后利用HFSS三维电磁仿真软件进行仿真分析,通过仿真结果得出两个阻带各自的3 dB截止频率和谐振频率并求出对应的等效电感值和电容值,分析参数变化对等效电路的影响.
2.1 方格对蛇型DGS的影响
基于图1所示的蛇型DGS结构,取导带宽为w=2.4 mm、方格的宽b=5 mm、蛇型缝隙的宽度g=0.38 mm、U形拐点数n=6,改变方格的长a,分别取a=3,4,5,6和7 mm对应的仿真结果如图5所示.随着方格长a的增大,截止频率和谐振频率相应地减小,且减幅越来越小.利用公式(1)、(2)计算得等效电路的电感值随a的增大而增大,电容值基本保持不变,其中等效电感值L1增幅明显.

图5 方格长a对蛇型DGS的影响Fig.5 Effect of square long (a) on snake DGS
取导带宽为w=2.4 mm、方格的长a=5 mm、蛇型的宽度g=0.38 mm和U形拐点数n=6,改变方格的宽b,分别取b=3,4,5,6,7 mm对应的仿真结果如图6所示.随着方格宽度b的增大截止频率和谐振相应地减小,第二个阻带基本不变,主要影响第一个阻带.利用公式(1)、(2)计算得等效电路的电容值随b的增大而减小,相反电感值随之增大,其中电感值L1和电容值C1变化明显.
2.2 缝隙对蛇型DGS的影响
基于图1所示的蛇型DGS结构,取导带宽为w=2.4 mm、方格的长a=5 mm、宽b=5 mm和蛇型的U形拐点数n=6,改变蛇型的宽g,分别取g=0.2,0.29,0.38,0.47,0.56 mm,对应的仿真结果如图7所示.随着g的增大,截止频率和谐振频率相应地增大,其中截止频率fc1增幅不明显.利用公式(1)、(2)计算得等效电路的电容值随g的增大而减小,电感值随g的增大略微增大,其中电容值C2减幅明显.
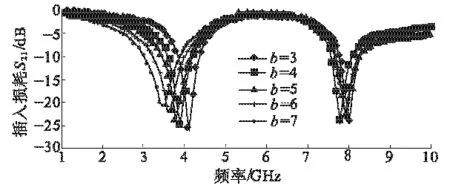
图6 方格宽b对蛇型DGS的影响Fig.6 Effect of square distance (b) on snake DGS

图7 缝隙宽对蛇型DGS的影响Fig.7 Effect of gap distance on snake DGS
2.3 拐点数对蛇型DGS的影响
取导带宽为w=2.4 mm、方格的长a=5 mm、宽b=5 mm和蛇型宽g=0.38 mm,改变蛇型的U形拐点数n,分别取n=2,4,6,8,对应的仿真结果如图8所示.随着U形拐点数n的增大,截止频率和谐振频率相应的减小而幅度较小.利用公式(1)、(2)计算得等效电路的电感值L2随n的增大而减小,电容值变化随之增大,其中电容值C2增幅明显.

图8 U型拐点数n对蛇型DGS的影响Fig.8 Effect of U-shaped inflection point number (n) on snake DGS
综上所述,可以通过改变蛇型DGS结构的参数a,b,g和n来实现不同要求的带隙中心频率,在后面的滤波器设计中我们可以通过有目的调节参数a,b,g和n,实现滤波器的优化设计,从而确定DGS- LPF中DGS的尺寸.
3 DGS低通滤波器的设计
LPF与DGS结构的等效电路相似,都是由集总等效元件组成.因此,基于DGS结构的等效电路法设计的LPF可进行电路分析[9,14-15].笔者提出含有DGS缺陷结构的低通滤波器LPF来验证等效电路法的正确性与可行性.如图9所示,低通原型滤波器由串并联电容电感组合而成,笔者设计滤波器时,串联电感用DGS结构来实现,而并联电容由大范围补偿的传输线来实现,即图10中w2=15 mm.以DGS-LPF为例验证设计方法的正确性,采用图1提出的蛇形DGS结构,参数分别设为a=b=5 mm,n=6,g=0.38 mm,w1=2.4 mm.通过等值代替得出DGS-LPF的等效电路如图11所示.其中,4阶LPF的等效电路中的两个并联的LC串联电路用DGS结构代替,并联电容C1和C2由低阻抗传输线代替,从而得出DGS-LPF的结构示意图如图10所示.根据文献[8]中滤波器的设计原理,将原型LPF转化成集总元件表示,并利用公式(4)、(5)表示出电感值与电容值.其中Z0为负载阻抗、gn为低通原型滤波器的反归一化参数(n=1,2).

(4)

(5)

(6)

图9 DGS-LPF原型电路Fig.9 The prototype circuit of DGS-LPF
用图1中所示的蛇型DGS结构代替图9中电感Ll,L2,利用式(4)、(5)和(6)计算出集总元件wcn,Ln,Cn的值.由公式(7)求出宽为15 mm、电容值分别为C1和C2的低阻抗传输线的长度l1=4.732 4 mm、l2=1.460 0 mm.其中λg和Z分别为15 mm传输线对应的电长度和阻抗值.同时,由于微带线存在额外等效电感La,因此,利用公式(8)将额外的电感考虑在等效电路的LC电路中,最终确定等效电路的各个参数值.在HFSS和MATLAB环境下分别对含有DGS的LPF进行电磁仿真和等效电路仿真,结果如图12所示.
(7)
(8)
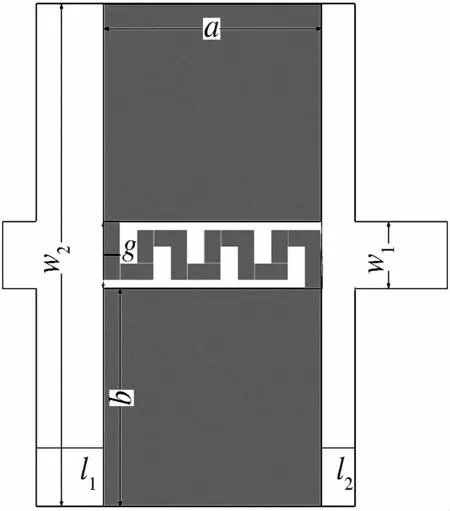
图10 DGS-LPF示意图Fig.10 Schematic view of DGS-LPF

图11 DGS-LPF等效电路模型Fig.11 Equivalent circuit model of DGS-LPF

图12 DGS-LPF的电磁仿真与等效电路仿真Fig.12 Simulation of electromagnetic and equivalent circuit of DGS-LPF
由图12可知,提出的等效电路合理地考虑了蛇型DGS单元的两个谐振频率,使基于等效电路的LPF的设计更符合实际.该滤波器在3.2 GHz和7.5 GHz处产生两个阻带,能有效地截止高次谐波.DGS低通滤波器的等效电路的电路仿真与电磁仿真结果在谐振w01之前拟合良好,且计算结果wc1=2.202 GHz,与仿真结果wc1=2.247 GHz相差也不是很大,证明了该设计方法的正确性.同时,在现实设计中可以根据不同的频率要求选取蛇型DGS的具体参数.
4 结论
笔者在哑铃型DGS结构的基础上提出了一种蛇型缺陷接地结构,并给出了其等效电路模型.与传统哑铃型DGS相比,该结构在不增加缺陷面积的情况下获得的衰减频率更低,产生的谐振频率点更多.结果表明,随着方格面积的增大,截止频率降低;随着缝隙宽度g的增大,截止频率升高;随着U形拐点数n的增加,截止频率降低.采用蛇型DGS设计的LPF等效电路的MATLAB仿真与HFSS电磁仿真结果相吻合.证明了该设计方法的正确性.
[1] PARK J I, KIM C S, KIM J, et al. Modeling of a photonic bandgap and its application for the low-pass filter design[C]//Asia-Pacific Microwave Conference.Singapore, 1999: 331-334.
[2] 林强, 张祖荫,郭伟. DGS微带线滤波器设计[J].现代雷达,2005,27(6):52-54.
[3] 刘海文,李征帆,孙晓玮,等.一种新颖的蝴蝶结形缺陷接地结构微带线[J]. 红外与毫米波学报,2004,23(6):431-345.
[4] DAL A, PARK J S, KIM C S, et al. A design of the low-pass filter using the novel microstrip defected ground structure [J]. IEEE Trans on Microwave Theory and Tech, 2001, 49(1): 86 -93.
[5] 顾继慧,杨一飞,周虹,等.新型缺陷接地结构带通滤波器研究[J].南京理工大学学报:自然科学版,2009,32(6):763-766.
[6] PARK J-S, YUN J-S, PARK C S. DGS resonator with interdigital capacitor and application to bandpass filter design[J]. Electronics Letters, 2004, 40(7): 433-434.
[7] KIM C S, LIM J S, NMA S, et al. The equivalent circuit modeling of defected ground structure with spiral shape[J]. IEEE Electronics Letters, 2002, 38(9):2125-2128.
[8] 曹锐, 孙振鹏.DGS结构特性分析及其改善微波放大器谐波[J].合肥工业大学学报:自然科学版,2007,29(11):1380-1383.
[9] LIM J, KIM C S, AHN D, et al.Design of low-pass filters using defected ground structure[J]. IEEE Trans. On Microwave Theory and Tech, 2005,53(8): 2539-2545.
[10]INSIK C,BOMSON L. Design of defected ground structures for harmonic control of active microstrip antenna[C]//IEEE Antennas and Propagation Society International Symposium, 2002(2): 852-855.
[11]丁勇. 基于SGS的UWB滤波器设计[J].电子元件与材料,2013,32(9):42-44.
[12]KHAN M T, ZAKARIYA M A, SAAD M N M,et al. Parametric effect of defected ground structure (DGS) on frequency of a bandpass filter [C]//IEEE International RF and Microwave Conference,2013:184-188
[13]KUMAR A, VERMA A K. Control of stop band using spur line resonators of DGS based low pass filter [C]//IEEE Students’ Technology Symposium. 2011:61-64.
[14]LIM J S, KIM C S, JEONG Y C, et al. An advanced equivalent circuit of spiral-shaped defected ground structure[C]//34th European Microwave Conference.Amsterdam, 2004:1357-1360.
[15]LIM J S,KIM C S LEE Y T, et al.A new type of low pass filter with defected ground structure[C]//Microwave Conference. European,2002:1-4.
Design of Snake DGS Microstrip Filter
WANG Ke, CHEN Xiao-qiang
(College of Automation and Electrical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)
A snake DGS defect structure which uses snake-like gap instead of rectangular gap into the dumbbell DGS is introduced. An equivalent circuit is built, meanwhile, the relevant circuit parameters are derived. Control variate method is used to analyze the influence of parameters variation to frequency characteristics and circuit characteristics of the snake DGS defect structure. Furthermore, this kind of structure is put into the design of low-pass filter, simulation of the designed filter and its equivalent circuit model is done separately by MATLAB and HFSS. The results of these two methods are coincident. So it can be drawn that the structure has lower attenuation frequency and more resonant frequency in the case of maintaining the area of the defects.
defected ground structure; equivalent circuit; low-pass filter
2014-09-30;
2014-11-19
国家自然科学基金资助项目(51167009/E0703);铁道部重点资助项目(2011X008-D)
陈小强(1966-),男,甘肃天水人,兰州交通大学教授,博士,主要从事计算电磁学、计算机仿真与控制方面的研究,E-mail: xqchen@mail.lzjtu.cn.
1671-6833(2015)01-0015-05
TN817
A
10.3969/j.issn.1671-6833.2015.01.004

