无需配对的无证书门限签名方案

杨邓奇，杨 健

（大理学院数学与计算机学院，云南大理 671003）

Client/Server计算模式中，服务器通常可以作为证书管理中心，负责系统中公钥证书的管理工作，同时亦可作为签名者一些重要的消息提供签名服务，如身份分配、令牌发布时所需消息的签名等。然而，一方面，在纯分布式系统中找到一个可靠的节点作为中心服务器来管理数字证书、提供签名服务是个困难的问题；另一方面，当系统规模较大时，由单一的服务器提供签名服务可能导致系统瓶颈的产生。因此，有学者提出基于秘密共享技术的门限签名方案〔1-7〕，由多个节点共同为一些重要消息提供签名服务。现有的门限签名方案可以分为3 类：①基于PKI 的门限签名技术；②基于身份密码系统（IBC）〔8〕的门限签名技术〔1〕；③基于无证书公钥密码系统（CL-PKC）〔9〕的门限签名技术。但是，基于PKI技术的门限签名技术需要进行复杂的证书管理，导致系统效率低下；基于IBC 的门限签名方案存在密钥托管问题；基于CL-PKC 的门限签名方案克服了PKI 方案和IBC 方案中的效率和安全问题，具有更高的效率和更好的安全性。现有的无证书签名方案主要是基于双线性对映射〔10〕设计，双线性对运算是个非常耗时的操作〔11〕。因此，基于双线性对的无证书门限签名方案的效率较低。

本文基于无信赖者的秘密共享技术和无双线性对无证书密码系统，设计无证书门限签名方案。方案安全性基于椭圆曲线离散对数问题（ECDLP）〔11〕，方案涉及主要运算为有限域上椭圆曲线标量乘法（即点乘运算）。该门限签名方案消除了基于CLPKC门限签名方案中耗时的双线性对运算，且不依赖可信中心来分发秘密共享技术中子密钥。分析表明，该方案具有更好的安全性和效率。

1 预备知识

无证书密码系统中存在一个密钥生成中心（KGC）参与用户私钥的生成。系统中，每个用户均有一个唯一用户身份标识（ID）；用户私钥均由两个部分构成，即KGC为其生成的部分私钥和用户自主选择的秘密值两部分。只有同时掌握部分私钥和用户秘密值，才能进行密码学的相关运算。

通用的无需配对的无证书签名方案包括以下7个算法：

1）Setup 算法：由KGC运行该算法，算法生成系统公开参数params 和系统主密钥s，即（params，s）=Setup（）。

2）PartialKeyExtract 算法：由 KGC 运行该算法，算法输入参数params，主密钥s和用户ID，输出用户部分私钥DID和对应的部分公钥PID，即（PID，DID）=PartialKeyExtract（params，s，ID）。

3）SetSecretValue 算法：由用户运行该算法，算法输入参数params和用户ID，输出用户自主生成的秘密值xID，即xID=SetSecretValue（params，ID）。

4）SetPrivateKey 算法：由用户运行该算法，算法输入参数params，用户部分私钥DID和用户秘密值xID，输出用户私钥 SKID，SKID=SetPrivateKey（params，DID，xID）。

5）SetPublicKey 算法：由用户运行该算法，算法输入参数params，用户部分公钥PID，用户部分私钥xID和用户ID，输出用户公钥PKID，即PKID=SetPublicKey（prarms，PID，xID，ID）。

6）Sign算法：由签名用户运行该算法，算法输入参数params，用户私钥SKID，用户ID 和消息m，输出签名σ，即σ=Sign（params，SKID，ID，m）。

7）Verify算法：由验证签名的用户运行该算法，算法输入参数params，用户公钥PKID，用户ID 和签名σ，输出验证结果“Accept”或“Reject”。

2 无需配对的无证书门限签名方案

本文考虑系统中没有可信中心服务器的纯分布式网络环境的门限签名技术。因系统中没有可信第三方，主密钥不能由单个节点掌握，秘密共享技术中打造和分发主密钥的子密钥（后称子主密钥）也不能由单个节点负责，即要求系统中没有任何节点单独掌握系统主密钥。因此，首选需要在系统中挑选若干个节点来共同协商系统的主密钥并为系统中的重要消息提供多节点共同签名服务。记选中的节点为SN，假设选择了n个节点，记为SNi（i=1，2，…，n），节点SNi对应的ID 记为设计无证书签名方案如下。

2.1 SN 初始化初始化阶段n个SN 节点协商系统公开参数 ＜p，q，G，P，P0，H1，H2＞，其中p，q为2 个素数，使得q|p-1；P是安全椭圆曲线上循环加法群的一个生成元；q是P的阶；H1:{0，1}*×G×G |→Zq*，H2:{0，1}*|→Zq*为两个哈希函数；P0为系统公开密钥，由n个SN节点按照下列方式协商生成：

1）SNi（i=1，2，…，n）随机选择一个秘密值bi∈GF（p）和一个t-1次多项式fi（x）：fi(x)=ai,0+ai,1x+…+ai,t-1xt-1modp，ai，j∈GF（p）（j=0，1，…，t-1），s.t.fi（0）=ai，0=bi，计算Bi，k=ai，kP（k=0，1，…，t-1）并将其发送给其他n-1个SN节点。

2）SNi（i=1，2，…，n）节点将其他n-1 个节点的ID 代入多项式，计算fi(IDSNj) 并将其通过安全信道发送给SNj（j=1，2，…n，j≠i）。

3）SNj收到来自其他n-1 个SNi（i=1，2，…n，i≠j）节点计算的fi(IDSNj)后，通过（1）式验证：

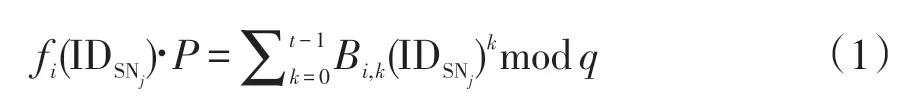
如果（1）成立，则fi(IDSNj) 是有效的，否则是无效的。

4）当SNi（i=1，2，…，n）收到所有来自其他n-1个SN 节点的fj(IDSNi)（j=1，2，…，n，j≠i）并验证其有效性后，计算并将其广播给其他n-1个SN节点。

5）SNi（i=1，2，…，n）收到来自其他n-1 个 SN节点的后，计算其 中令s=即为系统私钥，称为主密钥。P0=sP为系统公钥。令则si为SNi（i=1，2，…，n）所掌握的主密钥的子密钥，即子主密钥，需要保密。

2.2 SN 密钥生成在这个阶段，节点 SNi（i=1，2，…，n）生成自己的公私钥对。

1）SNi（i=1，2，…，n）随机选择秘密值，计算公钥Xi=xiP，Ri=riLiP，并将 ＜IDBNi,Ri,Xi＞发送给SNj（j=1，2，…，n，j≠i）。

2）SNi（i=1，2，…，n）收到来自其他n-1个节点的后，计算设 置 SNi的 公钥即为，私钥为

2.3 签名与验证

2.3.1 签名 假设用户A 需要对消息m进行签名，它首先从n个SN节点中选择t个，并告知每个SN节点它所选择t个SN 节点的ID 字符串，即广播给t个SN节点。然后将消息m发 送 给 签 名 节 点 SN1，SN2，…，SNt。 SNi（i=1，2，…，t）收到用户A 关于消息m的签名请求后，完成以下操作：

1）SNi随机选择计算Ti=aiP，并发送元组给SNj（j=1，2，…，t，j≠i）。

2）SNi收到来自其他t-1个SNj（j=1，2，…，t，j≠i）节点的所有元组后，计算σi=aie+γ(xi+DiLi)，生成消息m的子签名（σi，γ，Ti）并将其发送给用户A（此处，R和X可以通过预计算的方式以提高签名效率）。

2.3.2 验证 用户A收到来自t个SN节点的子签名（σi，γ，Ti）（i=1，2，…，t）后，计算Qi=σie-1∙P-并验证Qi=Ti是否成立，若成立，则接受σi；否则拒绝σi并请求SNi重签。

验证过程证明：

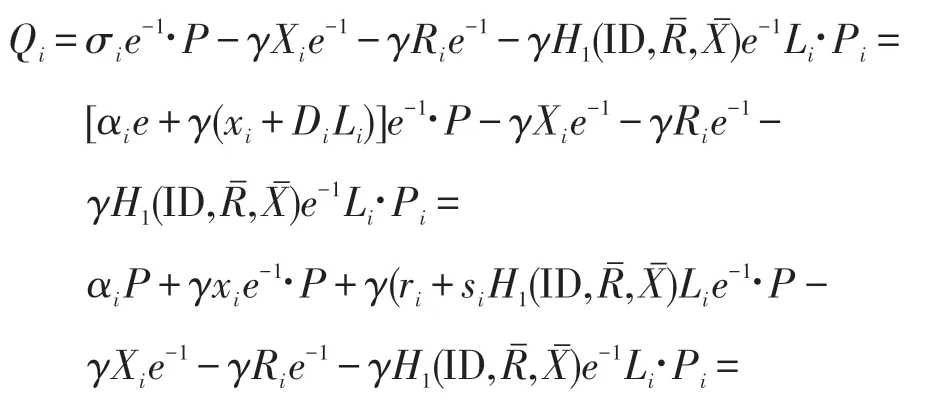
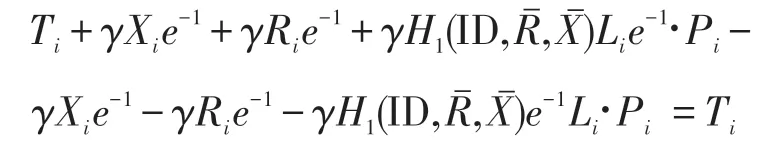
若所有σi（i=1，2，…，t）均通过验证，则用户A计算即为节点SN1，SN2，…，SNt对消息m的联合签名。

若系统中另一用户B 要对A 发送的带有SN 节点签名的消息m进行验证，则A 发送元组＜σ，γ，T，ID＞，其过程如下：

Q=σe-1∙P-γXe-1-γRe-1-γH1(ID,Rˉ,Xˉ)e-1∙P0，并 判断H1(ID,Q,X)=γ是否成立，若成立，则接受签名σ；否则拒绝签名σ。

验证过程的正确性证明:

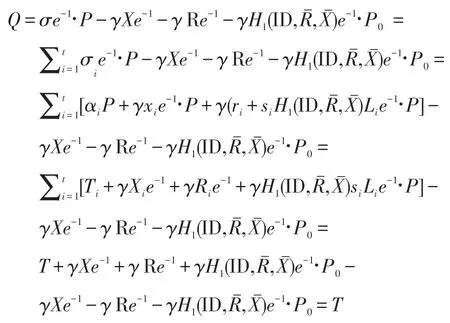
所以H1(ID,Q,X)=H1(ID,T,X)=γ。

3 安全与性能

3.1 安全性分析目前CL-PKC安全模型通常考虑两种类型的攻击：公钥置换攻击和主密钥攻击。在CL-PKC中，节点公钥为PK=＜X，R＞，私钥为SK=＜x，D＞，其中D=r+sH1（ID，R，X）为部分私钥。

1）公钥置换攻击

在公钥置换攻击中，攻击者可以置换用户的公钥，但不知道系统主密钥。在CL-PKC 中，用户私钥SK 与用户秘密值x、随机数r、用户身份标识ID和系统主密钥s相关。因为，攻击者不知道系统主密钥s，系统主密钥s参与部分私钥生成的计算是CL-PKC密码系统抵抗公钥置换攻击的基础。为方便起见，假设系统中的签名者为SNA，其发送＜IDA，PKA，m，Sign（m，SKA）＞ 给用户B。 用户 B 可以利用SNA的公钥PKA，身份标识IDA和系统公开参数params 来验证SNA的签名。如果攻击者C 要假冒签名者SNA的身份伪造签名，则攻击者C 选择秘密值x′A，随机数r′A，计算X′A=x′AP，R′A=r′AP，并用PK′A=＜X′A，R′A＞置换 PKA。然后攻击者 C 发送＜IDA，PK′A，m，Sign′（m，SKA）＞ 给用户B。假设签名算法是不可伪造的，则攻击者C 要生成一个能被PK′A验证的签名，则 C 必须掌握 PK′A对应的私钥SK′A。但是 SK′A=＜x′A，D′A＞，D′A=r′A+sH1（IDA，RA，X′A）。攻击者C 不知道系统主密钥s，因此，它无法计算部分私钥D′A。所以攻击者C 无法伪造一个有效的签名。

2）主密钥攻击

主密钥攻击中攻击者掌握系统主密钥，但不能置换用户公钥。如果攻击者C 要假冒SNA的身份伪造签名，它必须知道SNA公钥PKA对应的完整私钥SKA=＜xA，DA＞。但是因为攻击者C不能替换SNA的公钥，也无法知道SNA选择的秘密值xA，所以攻击者C 无法获取SNA完整的私钥，无法伪造有效的签名。

3）抗KGC主动攻击和共谋

文献〔8〕指出，CL-PKC 中，如果 KGC 发动主动攻击（即同时具有置换公钥的能力和访问系统主密钥的能力），则它可以伪造任何签名，亦可完成任何密码学操作。因此，所有当前无证书密码方案均不考虑攻击者同时具备这两种能力。在分布式系统中，很难找到一个绝对可靠的节点来充当KGC，因此，无法防止KGC 发动主动攻击。本文所提的方案，基于无信赖者的秘密共享技术，利用拉格朗日插值多项式f(x)，由n个SN 节点共同协商计算系统主密钥s，不依赖于任何单个可信赖节点，没有一个节点独立掌握完整的系统主密钥，故任何一个单独的SN 节点都无法发动KGC 主动攻击。对于t-1 次多项式来说f(x)，至少需要t对（ID，f（ID）），才能重构多项式，即至少t个SN 节点共谋才能重构出系统主密钥。因此，攻击者至少要获取t个si或至少t个 SN 节点共谋才能发动 KGC 主动攻击。

3.2 性能用P表示双线性对运算，E表示指数运算，S表示椭圆曲线上的点乘运算，H表示哈希运算。将本文所提的门限签名方案与现有方案进行性能比较如表1所示，其中nu和nm分别表示用户ID的长度和待签消息m的长度。

表1 性能比较

双线性对运算、指数运算和哈希运算的时间花费分别至少是椭圆曲线点乘运算时间花费的21倍、3倍和1倍。本文所提方案主要运算是椭圆曲线上的点乘运算，具有较高的运算效率。

4 小结

基于无信赖者的秘密共享技术和无需配对的无证书密码技术设计了无需配对的无证书门限签名方案。方案消除了基于PKI门限签名方案中复杂的证书管理工作，消除了基于IBC 方案中固有的密钥托管问题；同时方案去除了传统CL-PKC 中耗时的双线性对运算；方案不依赖于单个可信节点。因此，方案具有简单、安全和高效的特点。

〔1〕Anitha T N，Jayanth A. Efficient threshold signature scheme〔J〕. International Journal of Advanced Computer Science and Applications，2012，3（1）:112-116.

〔2〕Xu Qiuliang，Chen Tzer-Shyong. An efficient threshold RSA digital signature scheme〔J〕. Applied Mathematics and Computation，2005，166（7）:25-34.

〔3〕Wang Licheng，Gao Zhenfu，Li Xiangxue，et al. Simulatability and security of certificateless threshold signatures〔J〕.Information Sciences，2007，177（6）:1382-1394.

〔4〕Xiong Hu，Li Fagen，Qin Zhiguang. Certificateless threshold signature secure in the standard model〔J〕.Information Sciences，2010，23（3）:175-203.

〔5〕Yuan Hong，Zhang Futai，Huang Xinyi，et al. Certificateless threshold signature scheme from bilinear maps〔J〕. Information Sciences，2010，180（23）:4714-4728.

〔6〕黄梅娟.新的基于身份的门限签名方案〔J〕.计算机工程与数字，2013，41（4）:625-627.

〔7〕Sun Hua，Ge Yanqiang. On the Security of Certi_cateless Threshold Ring Signature without Random Oracles〔J〕.Journal of Computational Information Systems，2014，10（9）:3585-3592.

〔8〕Boneh D，Franklin M. Identity-Based Encryption from the Weil Pairing〔C〕//Int’l Cryptology Conf.Advances in Cryptology，USA.2001:213-229.

〔9〕Baek J，Safavi-naini R，Susilo W. Certificateless public key encryption without pairing〔J〕. Information Security，2005，3650:134-148.

〔10〕Zhang L，Zhang F.A method to construct a class of certificateless signature schemes〔J〕.Journal of Computers，2009，32（5）:940-945.

〔11〕Wang S，Liu W，Xie Q. Certificateless signature scheme without bilinear pairings〔J〕.Journal on Communications，2012，33（4）:93-98.