磁场引起的近藤单态退相干机制
陈明伦, 梁 敢, 曹艳华, 王礼胜, 勾庆东, 刘宇安, 周运志
(1. 井冈山大学物理系,吉安 343009; 2.美国山姆休斯顿州立大学物理系,亨茨维尔 77341;3.井冈山大学数学系,吉安 343009; 4.井冈山大学电子工程系,吉安 343009)
磁场引起的近藤单态退相干机制
陈明伦1, 梁 敢2, 曹艳华3, 王礼胜3, 勾庆东1, 刘宇安4, 周运志1
(1. 井冈山大学物理系,吉安 343009; 2.美国山姆休斯顿州立大学物理系,亨茨维尔 77341;3.井冈山大学数学系,吉安 343009; 4.井冈山大学电子工程系,吉安 343009)
磁场作为一个环境能够诱导近藤单态的退相干.我们采用格林函数方法,计算磁场下量子点耦合Aharonov-Bohm环系统的退相干特性,数值结果显示磁场引起的近藤单态的退相干是一个突然的过程.
量子点; Aharonov-Bohm环; 退相干
1 引 言
量子点(QD)又称为人造原子,具有朗道能级分布.电子通过量子点的输运实际上是电子与人造原子的碰撞散射过程.由于散射过程是一种量子力学效应,因此电子通过量子点的输运中,经典欧姆定律将失效.失效的原因是输运电子与量子点所在电子之间形成了一个特殊的量子态即近藤单态[1].
近藤单态的形成将打开一个新的通道从而有助于量子点电路输运电导的提升,可用于微电子技术领域.目前Intel的CPU微加工技术已达0.09微米,很快进入纳米量级.在微米量级经典欧姆定律还成立.一旦到了纳米量级,纳米量级电路上某些形状的缺陷将相当于一个量子点[3-5],量子效应近藤单态将显现,需要借助近藤单态来提升输运电导.
然而,在真实环境下近藤单态作为一个量子态很容易塌缩,我们称之为近藤单态退相干.目前我们已知的退相干因素有如下这些:相移探测机制[6]、Fano共振机制[7]、路径探测机制[8]、辐射机制[9]、偏压机制[10]、电流机制[11]、磁场机制[12]等.以上因素均是作为环境引起特殊量子态近藤单态的退相干.
磁场比如地磁作为一个无所不在的环境,不可避免要引起近藤单态的退相干[12],在本文中我们将通过新的方法仔细讨论磁场引起的退相干效应.采用格林函数方法,我们计算磁场下近藤单态的退相干特性,计算结果表明磁场引起的退相干是一个突然的过程.
2 模型及其哈密顿量
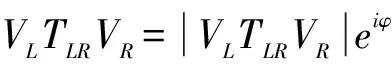
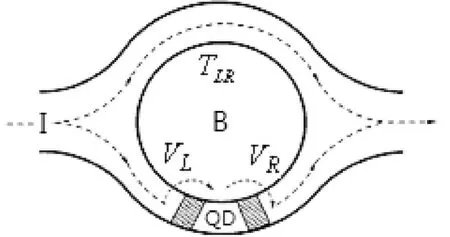
图1 量子点耦合Aharonov-Bohm环模型示意图Fig. 1 Schematic display of a quantum dot coupling to Aharonov-Bohm ring
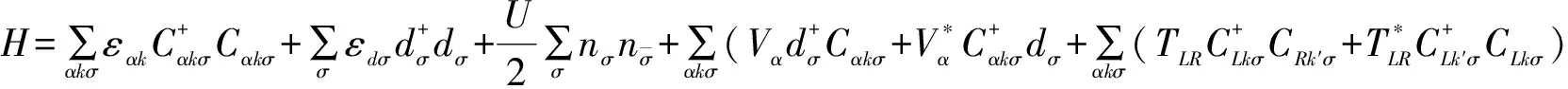
(1)
上式等号右边第一项是电子库的能带论哈密顿量,传导电子的量子态由波矢和自旋标记.第二项描述量子点单占据自旋简并局域态电子的哈密顿量,单占据自旋简并局域态是指接近电子库费米能级处的量子点最高填充能级的能态.该能级既可填充自旋向上的电子,又可填充自旋向下的电子,故称为单占据自旋简并局域态.由于量子点中电子很稀薄,不是费米液体,电子浓度低使得简并能量不能掩盖电荷间的库仑能,不存在库仑屏蔽效应,库仑强关联效应显现出来,不能形成能带只能形成一系列分离能级,电子数愈少能级间距愈大,因此称为人工原子,但又与一般原子不同,考虑强关联作用后,一旦量子点的单占据自旋简并态能级填充了一个电子,第二个电子即使自旋反向不违背泡利原理,也难以一起填充该能级.第三项描述两个局域电子之间的相互作用:第二个电子进入局域位置要比第一个电子花费更多的额外能量,这个额外能量称为充电能或叫在位关联能U,这是关键点,因为在位关联能U的存在使得单占据自旋简并态偏向于填充一个自旋电子.在这种情况下当量子点中总电荷为奇数时,由于单占据自旋简并态以下能级的电子两两配对,量子点的总自旋将为1/2,这时量子点的行为象一个磁性杂质.第四项描述下通道中电子以耦合强度Vkσ从源-漏电子库进入或离开量子点,该耦合称为s-d交换作用.第五项描述上通道中电子的输运.
采用我们发展的格林函数团簇展开方法[14],采用二阶截断,我们得到量子点耦合Aharonov-Bohm环系统的格林函数如下:
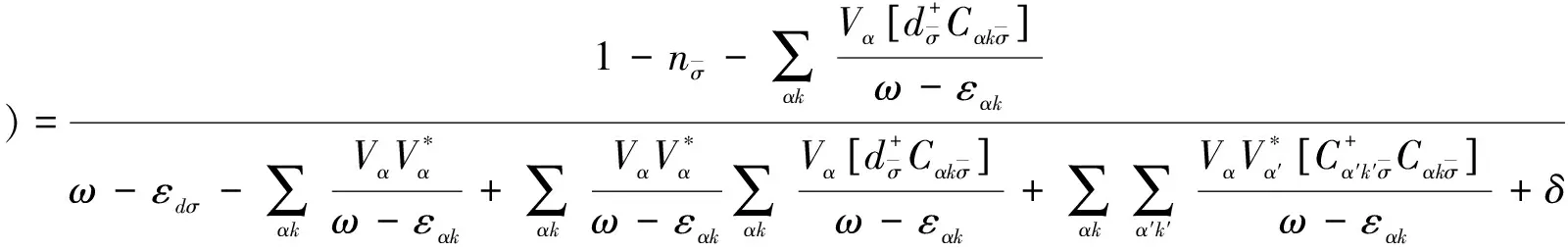
(2)
其中
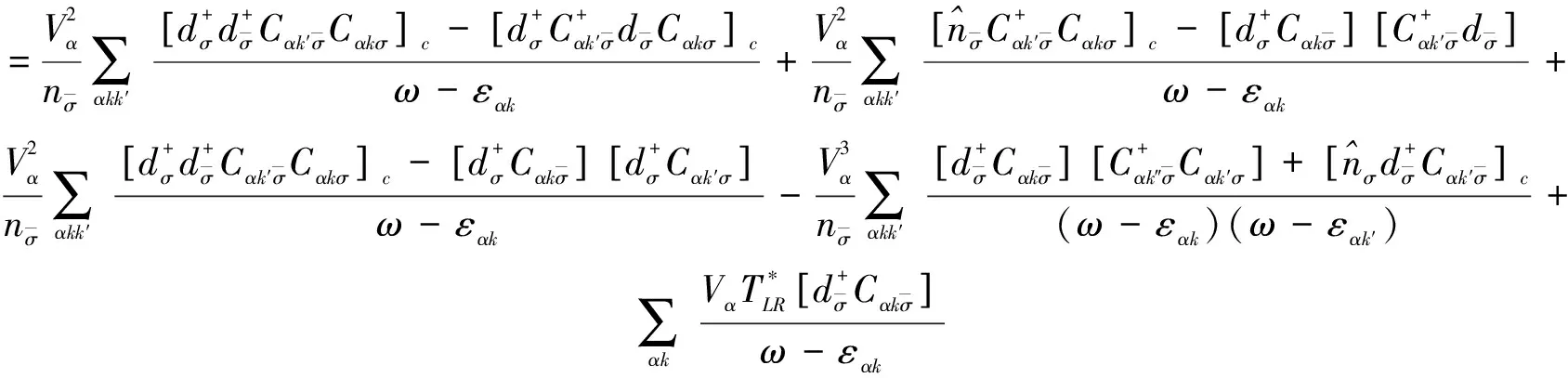
(3)
3 磁场引起的近藤单态退相干
得到量子点格林函数Gdσ(ω)后,根据下面公式[15]可计算电子通过量子点通道输运的微分电导:

(4)
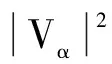
为了研究磁场对近藤单态的效应,我们计算了三种磁场情况下的微分电导:(a)B=0;(b)B=0.001T;(c)B=0.002T,计算结果见图2.
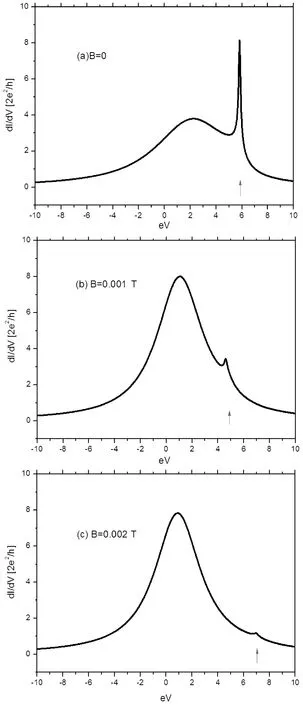
图2 微分电导随磁场的变化关系Fig. 2 The relationship between differential conductance and magnetic field
在图2a中,微分电导曲线显示一个非常狭窄的尖峰(红色箭头标记处),这就是实验上观测到的近藤峰[17,18],近藤峰的出现代表近藤单态形成,近藤峰的高度代表近藤单态的强度.在图2b和图2c中,近藤峰迅速下降并消失(红色箭头标记处),显示磁场的引入,诱导了近藤单态的退相干,并且这种退相干过程是突然的而不是渐进地.
4 结 论
近藤单态作为一个量子态会受到环境的影响,磁场作为一个无所不在的环境(比如地磁)必然诱导近藤单态退相干,我们的数值结果显示磁场引起的近藤单态的退相干是一个突然发生的过程.
[1] Hewson A C.TheKondoproblemtoheavyfermions[M]. Cambridge: Cambridge University Press, 1993: 100.
[2] Gregory S. Experimental-observation of scattering of tunneling electrons by a single magnetic-moment [J].Phys.Rev.Lett., 1992, 68: 2070.
[3] Appelbaum J. S-d exchange model of zero-bias tunneling anomalies [J].Phys.Rev.Lett., 1966, 17: 91.
[4] Wyatt A F G. Anomalous densities of states in normal tantalum and niobium [J].Phys.Rev.Lett., 1964, 13: 401.
[5] Ralph D C, Buhrman R A. Kondo-assisted and resonant-tunneling via a single charge trap-a realization of the Anderson model out of equilibrium [J].Phys.Rev.Lett., 1994, 72: 3401.
[6] Chen M L, Wang S J. Decoherence of Kondo singlet caused by phase-sensitive detection of Aharonov-Bohm interferometer [J].Mod.Phys.Lett. B, 2014, 28: 1450084.
[7] Chen M L, Chen Z Q. Decoherence of the Kondo singlet caused by Fano resonance [J].J.At.Mol.Sci., 2014, 5: 156.
[8] Aleiner I L, Wingreen N S, Meir Y. Dephasing in tunneling through a quantum dot: The “which path?” interferometer [J].Phys.Rev.Lett., 1992, 79: 3740.
[9] Kaminski A, Nazarov Y V, Glazman L I. Suppression of the Kondo effect in a quantum dot by external irradiation [J].Phys.Rev.Lett., 1999, 83: 384.
[10] Monreal R C, Flores F. Kondo resonance decoherence caused by an external potential [J].Phys.Rev. B, 2005, 72: 195105.
[11] Mitra A, Rosch A. Current-induced decoherence in the multichannel Kondo problem [J].Phys.Rev.Lett., 2011, 106: 106402.
[12] Pletyukhov M, Schuricht D, Schoeller H. Relaxation versus decoherence: spin and current dynamics in the anisotropic Kondo model at finite bias and magnetic field [J].Phys.Rev.Lett., 2010, 104: 106801.
[13] Anderson P W. Localized magnetic states in metals [J].Phys.Rev., 1961, 124: 4.
[14] Chen M L, Liang G, Cao Y H,etal. Differential conductance of electrons passing through a quantum dot[J].J.At.Mol.Phys., 2014, 31(1): 128(in Chinese) [陈明伦,梁敢,曹艳华,等.电子通过量子点输运的微分电导[J]. 原子与分子物理学报,2014, 31(1): 128]
[15] Meir Y, Wingreen N S. Landauer formula for the current through an interacting electron region [J].Phys.Rev.Lett., 1992, 68: 2512.
[16] Yacoby A. Coherence and phase sensitive measurements in a quantum dot [J].Phys.Rev.Lett., 1995, 74: 4047.
[17] Goldhaber G D, Shtrikman H, Mahalu D,etal. Kondo effect in a single-electron transistor [J].Nature, 1998, 391: 156.
[18] Cronenwett S M, Oosterkamp T H, Kouwenhoven L P A. Tunable Kondo effect in quantum dots [J].Science, 1998, 281: 540.
The decoherence of Kondo singlet caused by magnetic field
CHEN Ming-Lun1, LIANG Gan2, CAO Yan-Hua3, WANG Li-Sheng3,GOU Qing-Dong1, LIU Yu-An4, ZHOU Yun-Zhi1
(1.Department of Physics, Jinggangshan University, Ji’an 343009, China; 2.Department of Physics, Sam Houston State University, Huntsville 77341, USA; 3.Department of mathematics, Jinggangshan University, Ji’an 343009, China; 4.Department of Electronic Engineering, Jinggangshan University, Ji’an 343009, China)
The magnetic field can induce the decoherence of Kondo singlet as an environment. By employing the cluster expansion method, we calculate the differential conductance of a quantum dot coupling to Aharonov-Bohm ring under magnetic field. Our numerical results reveal that the decoherence of Kondo singlet, caused by magnetic field, is an abrupt process.
Quantum dot; Aharonov-Bohm ring; Decoherence
2014-07-13
国家自然科学基金(11164010)
陈明伦(1968—), 男,理学博士,教授,主要从事量子点输运的研究.E-mail: mlcen@126.com
103969/j.issn.1000-0364.2015.08.018
O561.5
A
1000-0364(2015)08-0631-04

