加劲肋布置方式对刚接柱脚力学性能的影响
赵滇生,蒋 丹
ZHAO Diansheng,JIANG Dan
(浙江工业大学建筑工程学院,浙江 杭州310014)
柱脚是建筑结构的重要组成部分,具有固定位置和传力的作用。合理设计柱脚节点以确保内力有效、可靠地传递给基础。柱脚中的加劲肋可以增加底板刚性,增大其转动约束能力[1]。本文主要运用有限元分析软件ABAQUS 研究加劲板布置方式对外露式钢结构柱脚力学性能的影响,从而讨论合理的加劲肋布置方式,为实际工程设计提供参考。
1 有限元柱脚模型参数
1.1 柱脚构件的选取
本文H 型钢柱的截面尺寸为H600 ×550 ×16×24,柱底板尺寸为950 mm×650 mm ×30 mm,加劲板高度为250 mm,厚度为15 mm,垫板的尺寸为80 mm× 80 mm × 20 mm,混凝土的长宽高取为1150 mm×850 mm×800 mm,锚栓采用M30。柱脚的组成构件钢柱、锚栓、底板和垫板均选用低合金钢Q345,钢材的屈服强度标准值为fy=345 MPa,弹性模量Es=2.06×105MPa,泊松比为0.3[2]。基础混凝土的强度等级为C30,其轴心抗压强度标准值fck=20.1 MPa,弹性模量Ec=3.00 ×104MPa,泊松比为0.2。考虑柱反弯点位于层高中部,取柱段1.5 m。
1.2 构件模型参数
柱脚的钢柱、加劲肋、锚栓、垫板和底板均采用C3D8I 进行模拟,采用双线性随动强化模型,混凝土选取C3D8R 进行模拟[3],采用多线性等向强化模型,Von Mises 屈服准则[4]。本文建立模型M1、M2、M3和M4四个柱脚模型,其平面图见图1。
2 有限元柱脚模型结果对比分析
2.1 柱脚极限承载力的对比分析
各柱脚模型的M-θ 曲线对比图见图2。

图1 模型构造及尺寸

图2 模型M1~M4 的M-θ 曲线对比图
由图2 可以得出模型M1、M2、M3和M4的屈服弯矩和屈服转角,见表1。
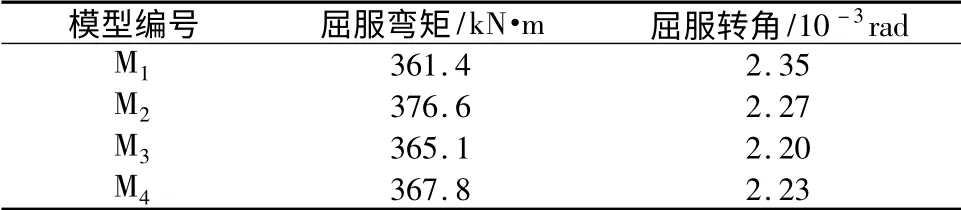
表1 模型M1~M4 的屈服弯矩和屈服转角
不同加劲肋布置方式的各个柱脚的初始转动刚度和抗弯极限承载力见表2。

表2 模型M1~M4 的抗弯极限承载力和初始转动刚度
由表2 可得,柱脚的初始转动刚度越大,其抗弯极限承载力就越大。由表2 中的数据可知,模型M2与模型M1相比,抗弯极限承载力由414.9 kN·m 增大到476.5 kN·m,提高了14. 8%,初始转动刚度由156 MN·m·rad-1增大到172 MN·m·rad-1,提高了10.3%;模型M3与M1相比,抗弯极限承载力由414.9 kN·m增大到456.6 kN·m,提高了10.1%,初始转动刚度由156 MN·m·rad-1增大到167 MN·m·rad-1,提高了7.1%;模型M4与M1相比,抗弯极限承载力由414.9 kN·m 增大到467.4 kN·m,提高了12.7%,初始 转 动 刚 度 由 156 MN·m·rad-1增 大 到169 MN·m·rad-1,提高了8.3%。由此可见,按模型M2、M3和M4的方式布置加劲肋均可提高柱脚的抗弯极限承载力和初始转动刚度,其中模型M2中加劲肋的布置对提高柱脚的抗弯极限承载能力效果最好。由模型M2、M3和M4的分析结果对比可知,底板区格数越多,柱脚抗弯极限承载力越大,由模型M3和M4的对比可知,当底板区格数相同,加劲肋划分各区格大小越均匀,柱脚抗弯极限承载力越大。这是因为区格划分得多而小,内力分布会更均匀,从而改善柱脚的受力性能。
2.2 构件截面转角的对比分析
各个柱脚中柱子和底板在弯矩作用下均产生一定的转角变形,其中在加劲肋高度处的钢柱截面应力较大,因此研究钢柱在此位置处的截面绕x 轴的转角;而底板则是研究其中面绕x 轴的转角。通过对各个柱脚模型中钢柱和底板转角的对比分析,得到变形较大的截面。构件中变形前为平面的截面,在变形后不再保持平面,因此取构件截面上两对称点在z 轴方向的位移来研究截面绕x 轴的转角。

图3 模型M1~M4 点的位移
图3 中点a1、点a2、点b1和点b2在模型中的位置见图1。从图3 中可以看出,柱脚处于弹性变形阶段时,随着弯矩的增加,位移变化很小,当柱脚钢材进入塑性阶段时,位移随时间变化很大,这与M-θ曲线关系一致。
根据图3 可以得出各点沿z 方向的位移,见表3。

表3 模型M1~M4 中各点沿z 方向的位移

表4 模型M1~M4 中构件截面绕x 轴的转角
从表4 可以得出,模型M1中θ1= 5. 97 ×10-3rad减小到θ2=4.36 ×10-3rad,降低了46.9%;模型M2中θ1= 46. 87 × 10-3rad 减小到θ2=30.98 ×10-3rad,降低了51.3%;模型M3中θ1=18.93 ×10-3rad 减小到θ2=12. 85 ×10-3rad,降低了47.4%;模型M4中θ1=31.22 ×10-3rad 减小到θ2=20.88×10-3rad,降低了50.0%。由此可见,4 个模型中的θ1均大于θ2,说明在弯矩作用下,加劲肋高度处的柱子截面比底板中面产生了更大的转角变形。
3 结 语
本文通过分析,可以得出以下结论:
(1)按模型M2、M3和M4的方式布置加劲肋均可提高柱脚的抗弯极限承载力和初始转动刚度;
(2)柱脚M1、M2、M3和M4均为刚性柱脚;
(3)在弯矩作用下,加劲肋高度处的柱子截面比底板中面产生了更大的转角变形。
[1]严正庭.最新钢结构实用设计手册[M]. 南宁:广西科学技术出版社,2003.
[2]陈绍蕃.钢结构设计原理[M].北京:科学出版社,1987.
[3]石亦平,周玉蓉.ABAQUS 有限元分析实例详解[M]. 北京:机械工业出版社,2007.
[4]王剑.探讨外露式钢结构柱脚加劲肋的布置方式[D]. 杭州:浙江工业大学,2013.

