多芯屏蔽电缆的串扰分析*

王剑强, 张国钢, 辛伟峰, 王 浩, 耿英三

(西安交通大学 电力设备电气绝缘国家重点试验室, 陕西 西安 710049)

多芯屏蔽电缆的串扰分析*

王剑强, 张国钢, 辛伟峰, 王 浩, 耿英三

(西安交通大学 电力设备电气绝缘国家重点试验室, 陕西 西安 710049)

利用多导体传输线模型,建立变电站内多芯屏蔽控制电缆的串扰计算模型。针对实际多芯屏蔽电缆的绞合结构,提出了对多芯屏蔽电缆传输线模型的分布电容及电感参数的修正方法。对KVVRP-22型19芯屏蔽电缆进行了理论计算与试验测量,证明了方法的有效性,为准确分析多芯屏蔽电缆中电磁干扰的传播规律提供了工程计算方法。

多导体传输线； 屏蔽电缆； 串扰计算； 绞合

0 引 言

变电站中存在大量的屏蔽控制电缆,承担变电站一次侧和二次侧的信号传输。随着超高压和特高压输电线路的建设和运行,变电站内的电磁骚扰在不断增强,尤其是变电站内常规的开关操作。由于隔离开关的动作速度相对较慢,会在变电站内产生幅值大、频率高、陡度高的暂态快速过电压(Very Fast Transient Overvoltage, VFTO)。VFTO会通过电流互感器和电容式电压互感器等测量设备直接耦合至与之相连的屏蔽电缆芯线,在电缆芯线末端造成骚扰,可能使二次侧的设备误动作或绝缘击穿[1]。

实际的屏蔽电缆芯线是通过成缆工艺绞合在一起的[2],利用传统的平行传输线模型会给计算结果带来很大的误差。本文利用多导体传输线理论建立了型号为KVVRP-22的19芯屏蔽电缆的串扰计算模型。根据电缆的实际结构,考虑芯线层与层之间绞合的影响,提出了对平行传输线模型的分布电容和电感矩阵进行修正的方法,使其能适用于实际电缆的工程计算。

1 平行多导体传输线模型

将屏蔽电缆内的n根芯线和屏蔽层看作是n+1个导体组成的多导体传输线系统,以屏蔽层为参考导体,可列出方程[3]：

(1)

(2)

式中: U——芯线相对于屏蔽层的电压向量； Z——n×n维的阻抗矩阵； I——芯线的电流向量； Y——n×n维的导纳矩阵。

运用相模变换方法[4],求解式(1)、(2),令

U(z)=TvUm(z)

I(z)=TlIm(z)

(3)

式中: Tv、Tl——相似变换矩阵。

将式(3)代入式(1)、式(2),得

(4)

(5)

式中: γ——传播系数。

由式(5)变换,得

(6)

其中,定义模态特性阻抗Zc为

(7)

由式(4)～式(7),可得

(8)

(9)

传输线两端的边界条件如图1所示。

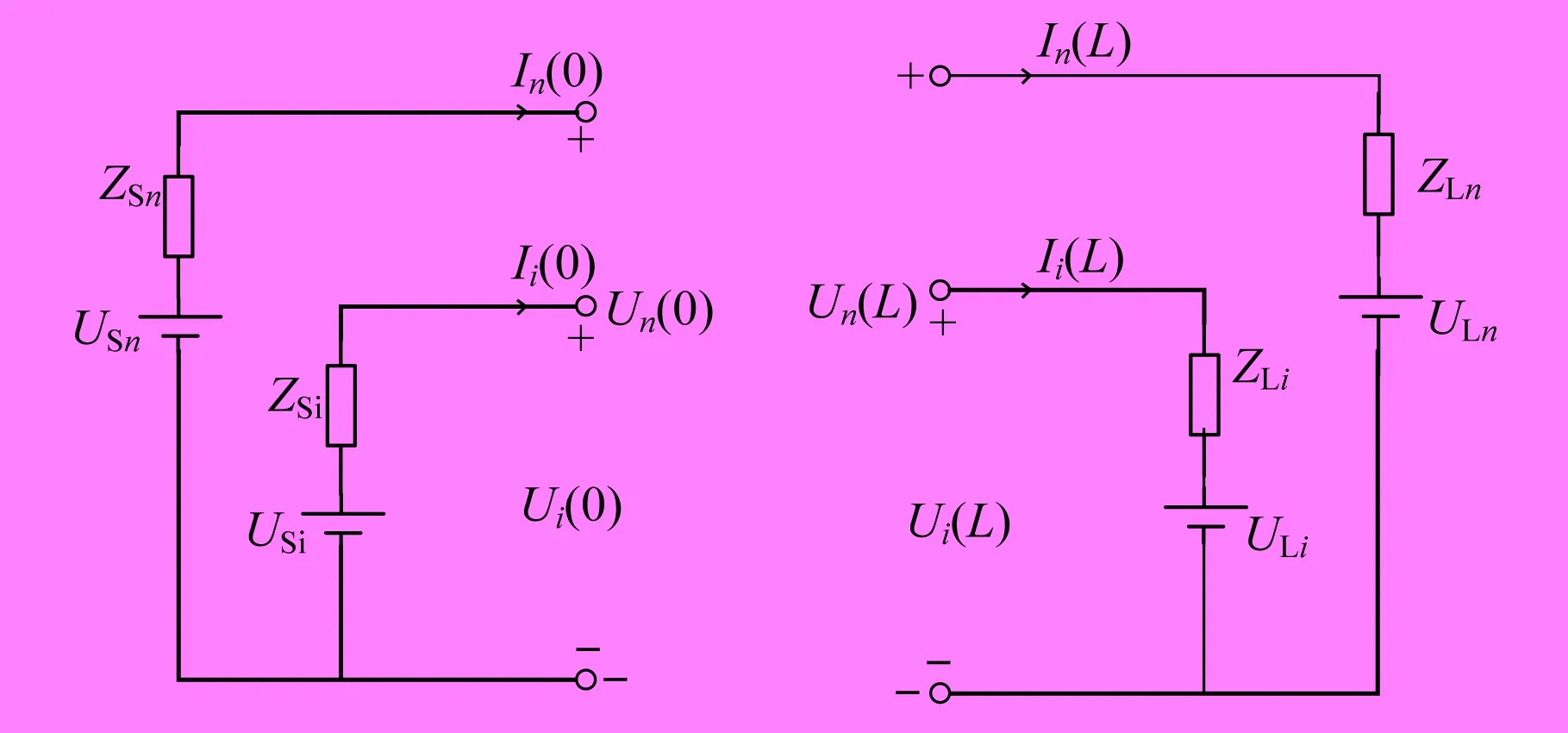
图1 传输线两端的边界条件

由图1可列出如下的边界方程：

U(0)=US-ZSI(0)

(10)

U(L)=UL+ZLI(L)

(11)

式中:US——始端干扰源； ZS——源侧阻抗矩阵； UL——负载侧干扰源； ZL——负载侧阻抗矩阵。

因此,由式(8)～式(11)可得

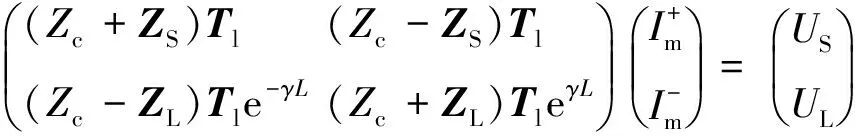
(12)

2 实际屏蔽电缆芯线间的串扰计算模型

将若干根绝缘芯线按照一定的规则绞合,并对芯线间的空隙进行填充和包带的工艺过程叫做成缆。直径相同的绝缘芯线的成缆称为对称成缆。实际多芯屏蔽电缆芯线的绞合结构如图2所示。

图2 实际多芯屏蔽电缆芯线的绞合结构

由于芯线间的绞合,使芯线末端的电压响应和芯线之间的串扰分析变得复杂,如果仍用传统的多导体平行传输线模型计算,会带来工程上不能接受的误差。

实际多芯电缆的芯线都是螺旋缠绕的,当绝缘芯线旋转一周,绝缘芯线沿轴向前进的距离称为电缆节距。在多芯屏蔽电缆中,中心芯线相对于其他芯线,其相对位置并没有改变,因此可以不用考虑因芯线之间的绞合对中心芯线的影响。对于每一层内部的芯线,芯线之间的相对位置也没有改变,无需考虑绞合产生的影响；对于不同层之间的芯线,由于芯线间的绞合,其相对位置会随着电缆节距作周期性的变化,此时就必须考虑绞合运动对芯线的影响。

有三层芯线的多芯屏蔽电缆截面图如图3所示。

图3 有三层芯线的多芯屏蔽电缆截面图

在图3中,将第二层芯线看作相对运动的参考体,第三层芯线围绕着第二层和中心芯线作绞合运动。在一个电缆节距内,最外一层的所有芯线相对于第二层和中间芯线而言其位置是等同的。从电路的角度上说,就是最外一层所有芯线与第二层和中间芯线的互电容和互电感相等,即

Ci,j=Cp

(13)

Li,j=Lp

(14)

式中:i——第二层芯线的编号,i=2,…,7；

j——最外一层芯线的编号,j=8,…,19；

Cp——最外一层芯线与第二层芯线的互电容值；

Lp——最外一层芯线与第二层芯线的互电感值。

在一个电缆节距内,对于第二层和中间芯线而言,最外一层芯线的位置刚好完成一次交换。因此,可以用没有绞合时芯线的互电容值来求Cp：

(15)

式中:N——芯线的数量,取19；N2——第二层芯线的数量,取6；N3——最外一层芯线的数量,取12。

根据修正后的电容矩阵,得

(16)

式中: C0——真空中求得电缆的电容矩阵； μ0——真空磁导率； ε0——真空介电常数。

将多芯电缆层与层之间的互电容和互电感分别用式(13)和式(14)代替,电容矩阵的其他电容值仍用平行传输线模型的电容值,将得到的考虑电缆芯线绞合后的分布电容、电感参数代入式(1)和式(2),就可用平行传输线模型求解实际绞合电缆的终端响应。

3 计算结果与试验结果分析

选取图3所示的长度为6 m的19芯屏蔽电缆。为分析方便,将电缆芯线按照从里到外逆时针编号。电缆截面编号示意图如图4所示。

图4 电缆截面编号示意图

芯线首段和末端均与屏蔽层开路,干扰源为信号发生器产生的250 kHz的方波,峰峰值约为1.94 V,方波的上升时间约为22 ns。电压干扰信号的波形如图5所示。

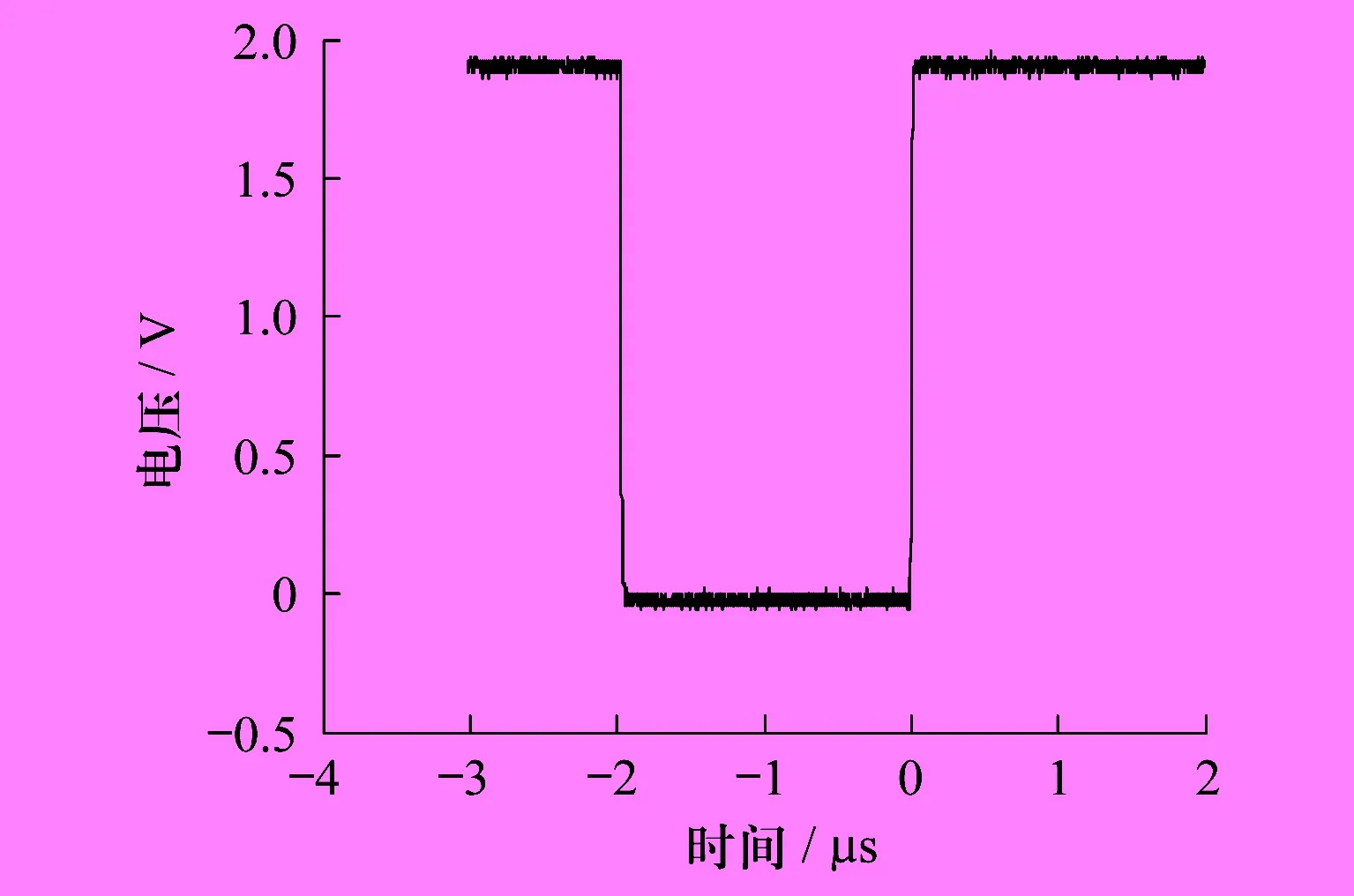
图5 电压干扰信号波形

19芯屏蔽电缆试验系统原理图如图6所示。示波器内阻为10 MΩ,采样时间间隔为1 ns,信号源内阻为50 Ω。

图6 19芯屏蔽电缆试验系统原理图

3.1 干扰源在芯线1#

将图5的电压干扰源加在芯线1#与屏蔽层之间。考虑芯线的对称排布,只计算芯线1#、2#、8#的终端电压响应。干扰源在芯线1#时计算结果与试验结果如表1所示。

3.2 干扰源在芯线2#

电缆芯线两端与屏蔽层开路,其他计算条件均不变,根据芯线的对称性,对芯线1#、2#、3#、4#、5#、8#所受到的骚扰进行分析。干扰源在芯线2#时计算结果与试验结果如表2所示。

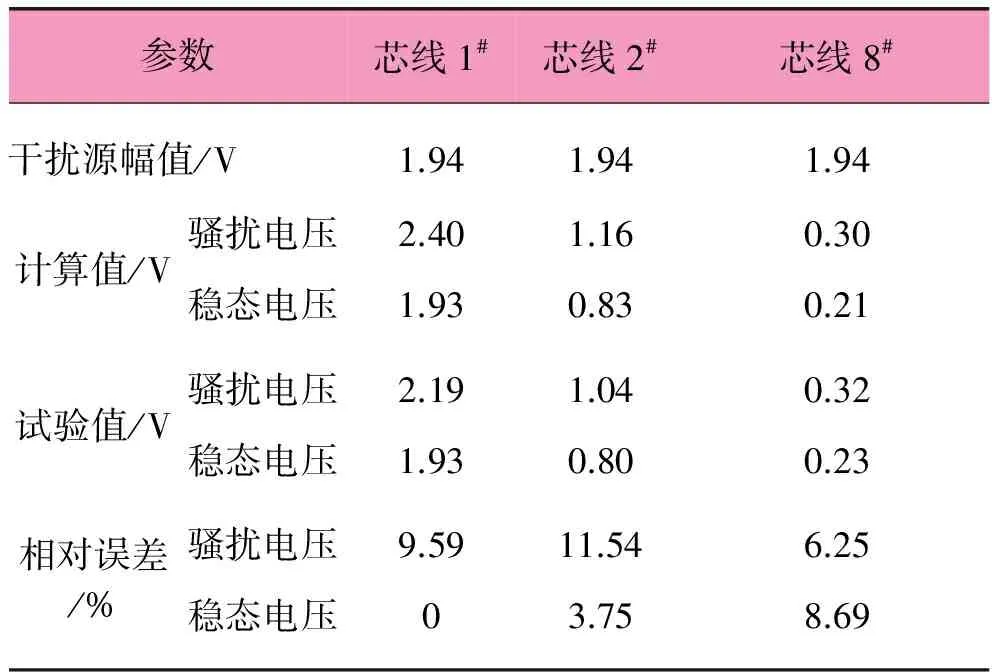
表1 干扰源在芯线1#时计算结果与试验值

3.3 干扰源在芯线8#

电缆芯线两端与屏蔽层开路,其他计算条件均不变,根据芯线的对称性,只分析芯线1#、2#、8#～14#末端所受到的电压骚扰。干扰源在芯线8#时计算结果与试验结果如表3所示。 表1～表3可知,当干扰源加在不同芯线时,计算结果与试验结果的趋势基本一致;稳态电压的最大误差为8.69%,发生在干扰源在芯线1#、计算芯线8#(最外一层芯线)末端电压响应时；最大相对误差为28.00%,发生在干扰源在芯线8#、计算芯线14#(离芯线8#最远的芯线)末端电压响应时。

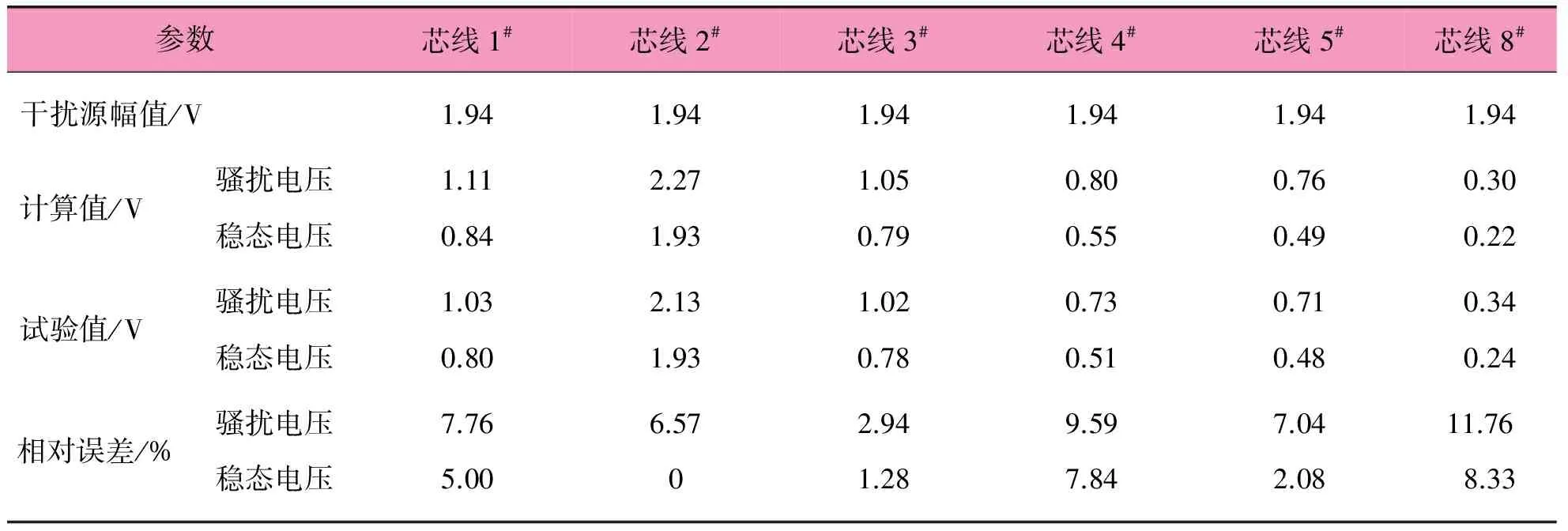
表2 干扰源在芯线2#时计算结果与试验值

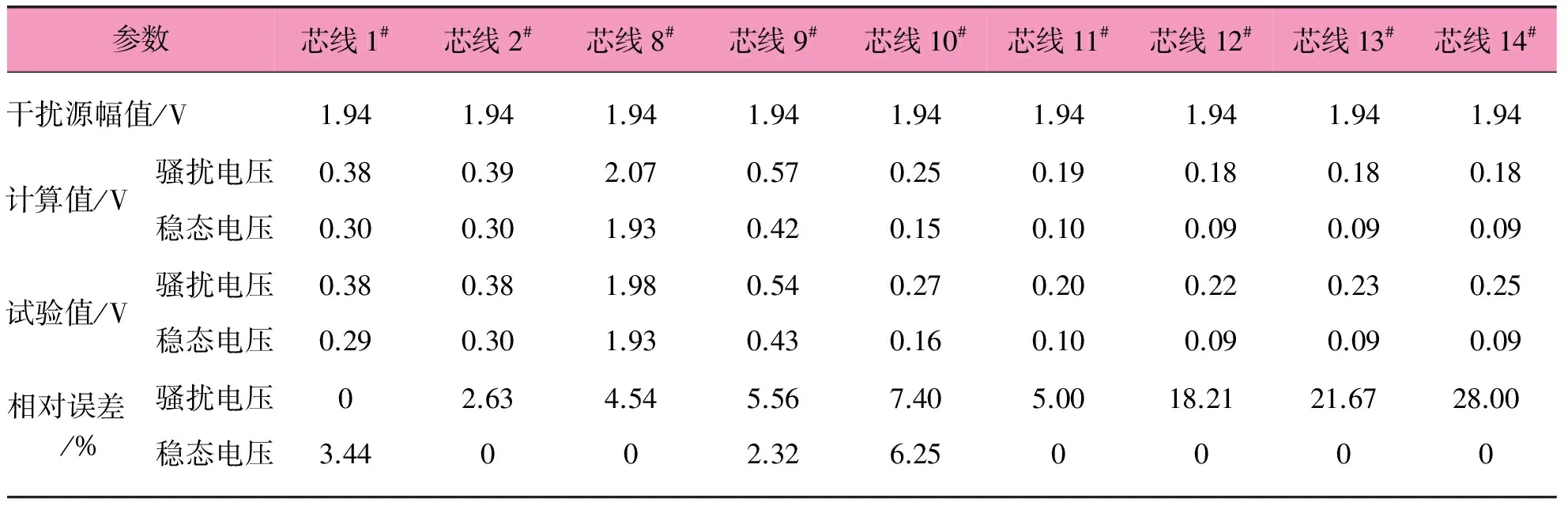
表3 干扰源在芯线8#时计算结果与试验值

误差产生的原因：

(1) 电缆长度不是电缆节距的整数倍。多余的最外一层芯线相对于中心芯线和第二层芯线而言位置将不再是等效的,多余的部分也就不能用本文方法对分布电容、电感矩阵进行修正。

(2) 对电缆屏蔽层进行了简化。实际电缆的屏蔽层为在一层类似塑料的绝缘纸上镀铜,模型中将其简化为相同厚度的铜皮,影响了屏蔽层阻抗计算。

(3) 忽略了电缆芯线间的挤压,将实际电缆内部芯线排列等效为有规则的圆周结构,从而对求得的分布电容、电感参数造成误差。

(4) 计算模型中忽略了测量引线的电阻、电感以及电容参数对试验结果的影响。

4 结 语

利用本文修正后的传输线模型计算了实际绞合的多芯屏蔽电缆的串扰。计算结果与试验结果表明,当干扰源加在不同芯线时,稳态值误差较小,基本满足一般工程计算的需要,验试了该方法的有效性。误差一方面是由于所选择的电缆长度不是整数倍的节距引起的,另一方面则是对实际电缆屏蔽层的简化引起的。

[1] 杨吟梅.变电站内电磁兼容问题 (二)： 变电站内主要干扰源及其特性[J].电网技术,1997,21(3)：72-75.

[2] 徐龙.电线绞制和成缆的三种 SZ方法的比较[J].电线电缆,1993 (5)：42-45.

[3] PAUL C R.Analysis of multiconductor transmission lines[M].Hoboken：John Wiley & Sons,2008.

[4] WEI C,HARRINGTON R F,MAUTZ J R,et al.Multiconductor transmission lines in multilayered dielectric media[J].IEEE Transactions on Microwave Theory and Techniques,1984,32(4):439-450.

[5] 衣斌,王泽忠.屏蔽电缆参数计算及屏蔽层与芯线间的串扰[J].高电压技术,2008,34(4)：804.

[6] 于刚,茆必成.开关操作暂态电压对变电所二次电缆的电磁干扰[J].电工技术杂志,2002 (12)：19-21.[7] TESCHE F M,KARLSSON T.EMC analysis methods and computational models[M].Hoboken：John Wiley & Sons,1997.

Crosstalk Analysis Between Core Wires of Shielded Cable

WANG Jianqiang, ZHANG Guogang, XIN Weifeng, WANG Hao, GENG Yingsan

(State Key Laboratory of Electrical Insulation and Power Equipment, Xi’an Jiaotong University, Xi’an 710049, China)

This paper has established the multi-conductor transmission lines of shielded cable in the substation to calculate crosstalk between core wires.For the twisted structure of the core wires,this paper has proposed a method to correct the distributed capacitance and inductance parameters of the multi-conductor transmission lines. The crosstalk between the core wires of KVVRP-22 19-core shielded cable were calculated by this method.It illustrated the effectiveness of this method to compare computed results with experimental results.This paper provides a more accurate engineering method to calculate the crosstalk between the core wires of shielded cable in the substation.

multi-conductor transmission line; shield cable; crosstalk calculation; twisted structure

王剑强(1988—),男,硕士研究生,研究方向为变电站电磁兼容。

电力设备电气绝缘国家重点实验室资助项目(EIPE3306)

2014-10-30

TM 201.4+4

A

1674-8417(2015)02-0005-05

张国钢(1976—),男,副教授,研究方向为智能电器理论与工程、电弧等离子体与电接触、新能源电力装备。

辛伟峰(1985—),男,博士研究生,研究方向为电器智能化理论与技术。

王 浩(1990—),男,硕士研究生,研究方向为电器智能化理论与技术。

耿英三(1963—),男,教授,博士生导师,研究方向为高压真空开断技术、电器智能化理论与技术、电器计算机辅助设计与仿真。