FAST馈源舱倾覆的理论分析及试验研究*

李铭哲，李 辉

(1. 贵州大学理学院，贵州 贵阳 550025；2. 中国科学院国家天文台，北京 100012； 3. 中国科学院射电天文重点实验室，北京 100012)

FAST馈源舱倾覆的理论分析及试验研究*

李铭哲1,2,3，李 辉2,3

(1. 贵州大学理学院，贵州 贵阳 550025；2. 中国科学院国家天文台，北京 100012； 3. 中国科学院射电天文重点实验室，北京 100012)

FAST望远镜馈源舱通过6根钢索悬浮于空中，在运行过程中其倾角连续变化，存在发生倾覆的风险。通过舱索系统的静力学理论分析和模型试验对FAST馈源舱的最大倾覆角进行了研究。基于舱倾角最大的优化原则和舱-索系统静力平衡，对索力和姿态角的限定等约束条件，建立了求解舱最大倾角(倾覆角)的目标优化函数，利用牛顿迭代法解得了舱在其运行轨迹面(焦面)的倾覆角，同时研究了重心改变对倾覆角的影响。通过舱索系统3 m缩尺模型对理论分析结果进行了验证，得到了模型舱在给定位置的倾覆角，试验结果与理论计算结果比较吻合。最后分析了馈源舱原型在整个焦面上的倾覆角，结果表明馈源舱在实际工作过程中是安全的，不会发生倾覆。

FAST望远镜；馈源舱；倾覆；静力学分析；模型试验

从1994年中国天文学家提出建造500 m口径球面射电望远镜(Five-hundred-meter Aperture Spherical radio Telescope, FAST)以来，国家天文台一直在全力推进其建设，FAST立项建议书在2007年7月10日得到国家发展改革委员会批准，现在于贵州省平塘县大窝凼地区全面建设中，建成后将成为世界上最大口径的单天线射电望远镜，在未来20年-30年保持领先地位。FAST拥有3项中国的自主创新技术——洼地台址、主动变形反射面和轻型馈源柔索拖动系统，突破了在地面建造全可动天线的百米工程极限[1]。

FAST的轻型馈源柔索拖动系统又称为馈源支撑钢索驱动系统，是一个空间尺度巨大的柔索牵引并联机器人，其机构主体是6根直径约50 mm的钢索及其相应的卷扬机，每根钢索和卷扬机依附于一座钢塔作为支撑架，6座塔均高达百余米，并按轴对称位置分布在直径600 m的圆周上。6根钢索共同支撑并牵引作为并联机器人终端控制平台的馈源舱在空中运动，使得馈源舱能够携带舱内设备(接收机)跟踪反射面的瞬时焦点，实现望远镜对目标星体的观测。馈源舱在空中的全部运动轨迹是一个曲率半径160 m，口径约206 m且与反射面同球心的球冠面，称为馈源焦面，如图1右下角。FAST馈源舱重约30 t，外接圆直径约13 m，是一个集结构、机构、测量、控制等相关技术于一体的光机电一体化的复杂系统，是FAST的核心部件，其主要功能是克服风扰和系统的其他扰动，通过馈源舱内的二次调整装置，实现馈源接收机的精调定位，如图1右上角。

馈源舱由钢索驱动在馈源焦面上运行时，姿态会发生变化，特别是从馈源焦面中心向边缘移动的过程中，倾角不断增大，因此运行过程中可能出现倾覆的危险，在运行过程特别是极限位置下是否会倾覆对观测及设备安全影响甚大，因此有必要对运行过程中馈源舱的倾斜状态进行研究。

FAST馈源舱的姿态与索力相关，文[2-5]对索牵引并联机构的静力学问题进行了分析。文[2]提出了钢索虚牵的判断标准及索力均匀的原则，并提出了确定Stewart 平台工作空间的方法；文[3]通过四绳索系统研究了塔分布圆半径对柔索牵引并联机器人工作空间及索力的影响，提出了新的判断准则解决绳索虚牵的问题；文[5]研究了进舱缆线对柔索牵引并联机器人工作空间的影响以及塔高度及馈源舱重心的改变对优化结果的影响。上述文献均基于索力优化进行求解，未曾考虑馈源舱的倾覆问题，亦未考虑馈源舱重心的改变对馈源舱最大倾覆角的影响。

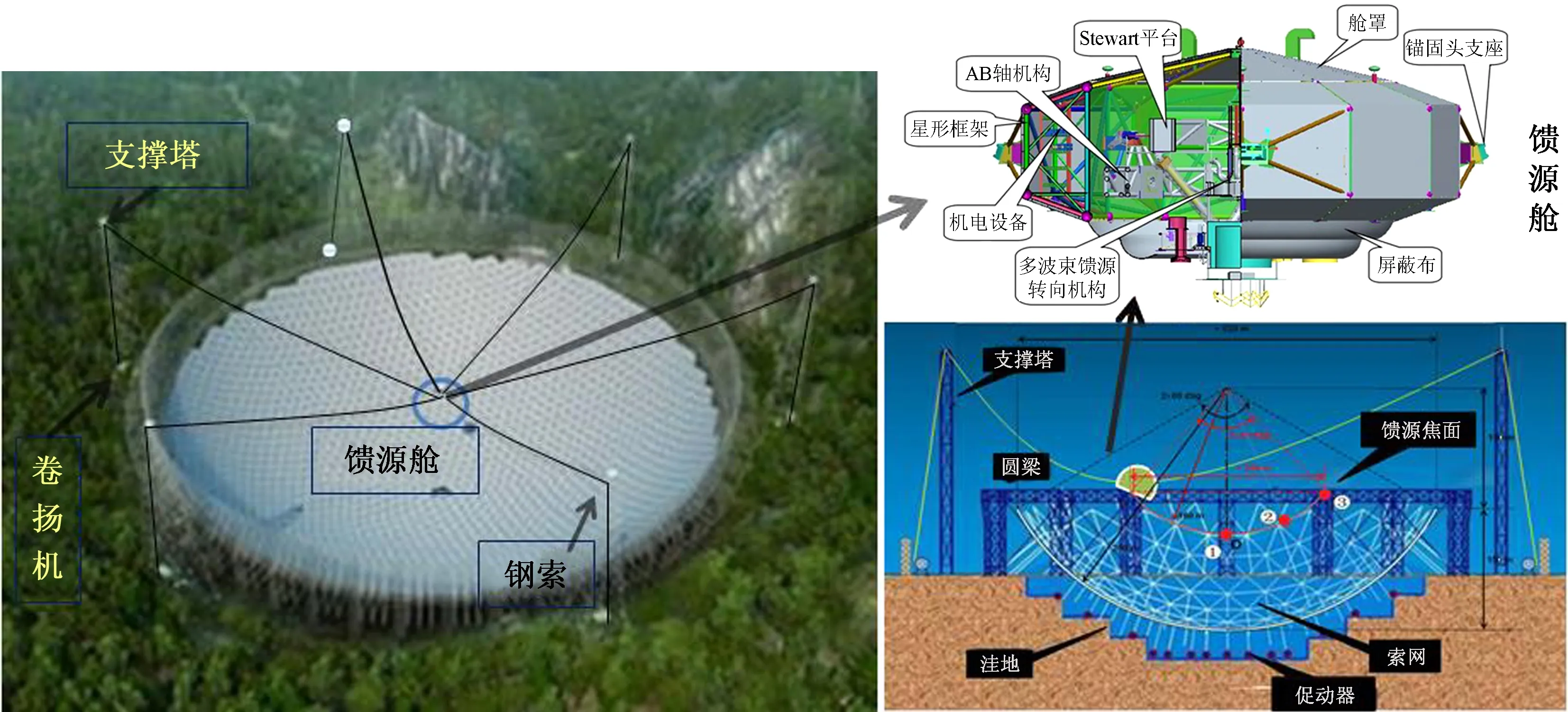
图1 FAST全景图及剖视图

本文试图通过理论建模的方法求解处于给定位置的馈源舱临界倾覆角，然后通过缩尺模型试验验证理论分析的结果。基于上述方法最后求解原型中馈源舱的临界倾覆角，分析其是否处于安全范围。

1 舱临界倾覆角的理论分析

以馈源舱和6条支撑钢索构成的舱-索系统为研究对象，分析馈源舱在不同姿态角时的静力平衡状态及6索的张力，求解馈源舱保持静力平衡的最大倾角，即馈源舱的临界倾覆角。

理论分析基于以下假设：

(1)馈源舱等效为6自由度刚体；

(2)支撑索简化为柔软不可伸长、具有一定质量且只能单向受拉的软绳；

(3)钢索曲线近似为抛物线。

如图2，在舱体质心位置按右手螺旋分别建立局部坐标系ox0y0z0和oxyz，全局坐标系为OXYZ，全局坐标系以主动反射面最低点为原点，Z轴方向向上。局部坐标系以模型舱的质心作为原点，z轴正向竖直向上，坐标系ox0y0z0固连于舱体并随舱姿态的改变而旋转，oxyz不随舱姿态的改变而变化，则可以建立舱体静力平衡方程组。

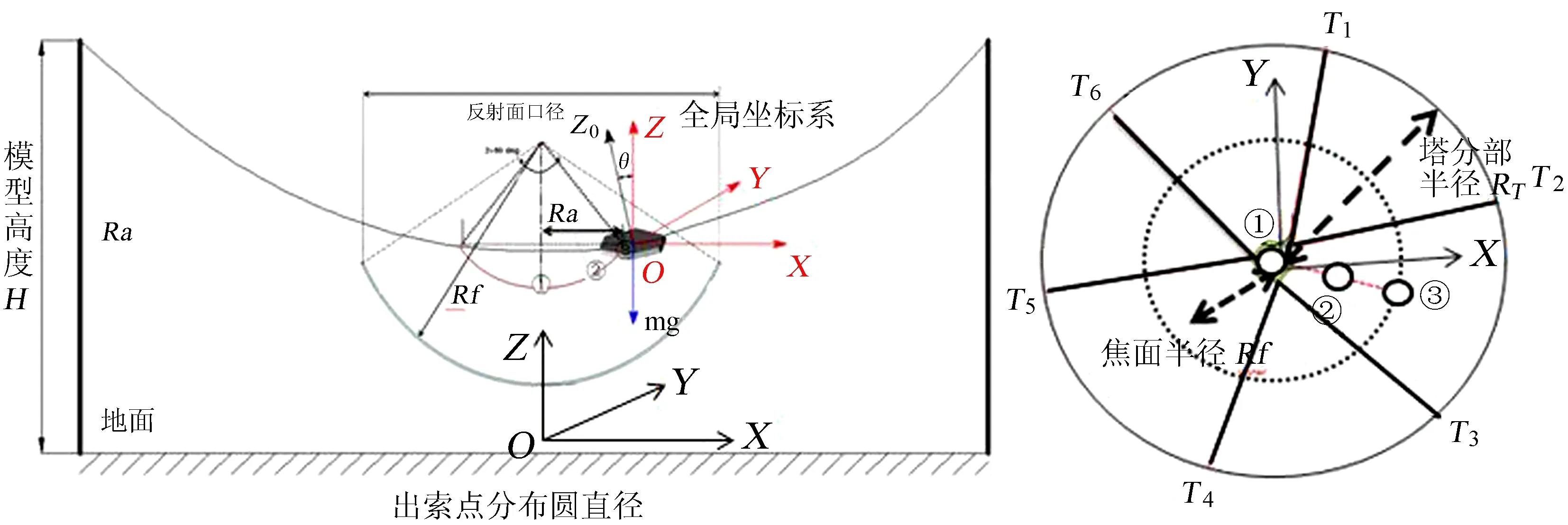
图2 FAST索力分析坐标系示意图

(1)式为空间力系沿X轴、Y轴、Z轴方向的平衡方程，(2)式为绕X轴、Y轴、Z轴的空间力矩平衡方程。Hi为第i根索张力的水平分量；αi为第i根索在XOY平面内的投影与X轴正方向的夹角；βi为第i个索舱接点处索张力矢量与XOY平面的夹角；G为馈源舱重量，如图(3)，xm、ym分别为馈源舱重心在全局坐标下的坐标；由此可以建立第i根悬索的静力微分方程：

(3)

以支撑索左端为坐标原点，水平方向为x轴，如图4。

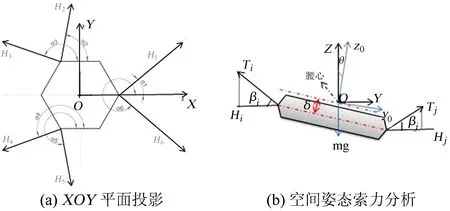
图3 馈源舱静力平衡分析

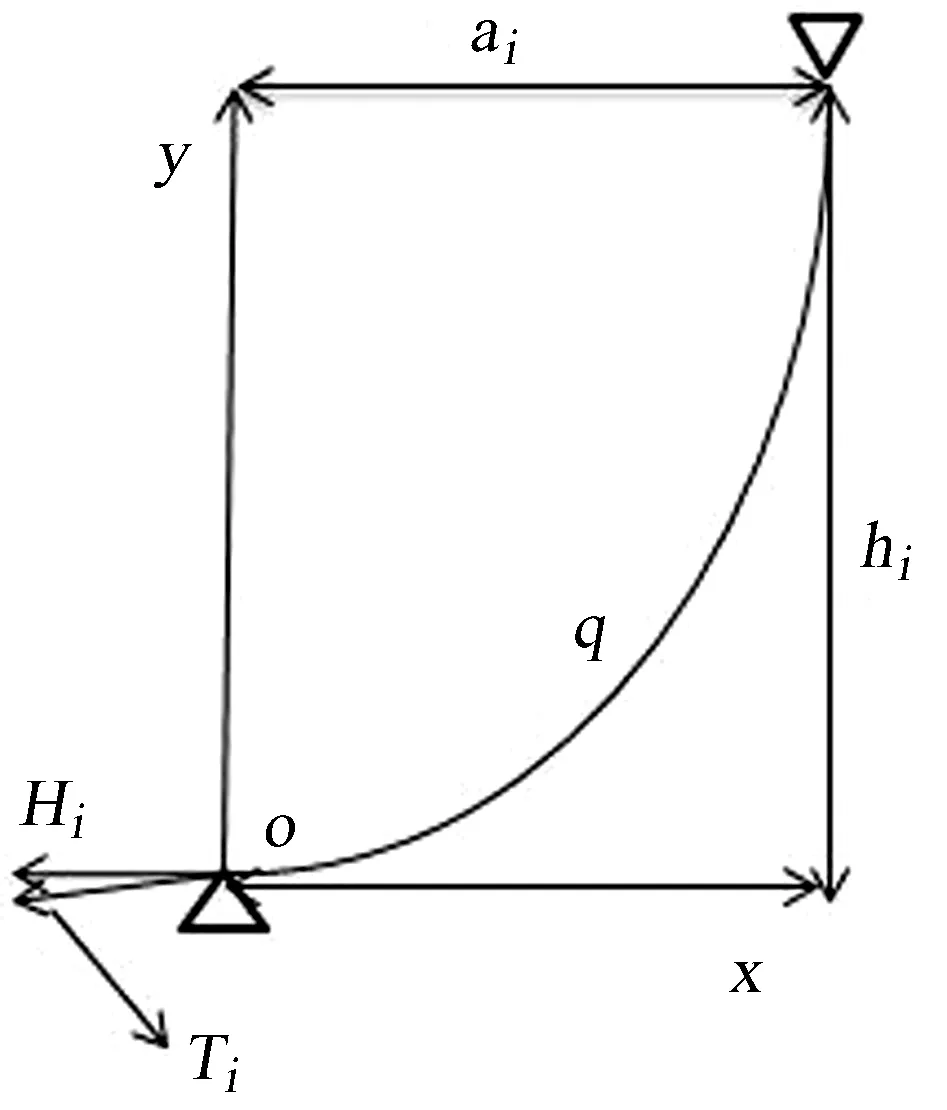
图4 索模型静力分析

得(3)式的抛物曲线近似解为

(4)

因此可以建立夹角βi与Hi的函数关系式为

(5)

其中符号ai、hi分别为从第i座支撑塔出索点到第i个索舱接点的相对水平距离和垂直高度；q为单位长度索自重；Hi为第i根绳索的拉力，如图4，Tani表示第i根绳索对应的高度差与跨度的比值，即Tani=hi/ai。

(1)式与(2)式中xi、yi和zi为第i个索舱接点的坐标，它们与局部坐标x0i、y0i、z0i的关系为[6]

(6)

式中的局部坐标x0i、y0i和z0i为已知量，仅取决于索舱接点在锚接平面的相对位置；θ、φ、φ表示馈源舱旋转的3个独立的空间姿态角，分别表示舱体的俯仰角、方位角和自旋角。如图3，θ定义为Z轴与z0轴之间的夹角，即本文需要求解的最大倾角；φ定义为z0轴在xoy平面内的投影与x轴正方向的夹角；φ定义为星形桁架绕z轴的旋转角；Sφ表示角度φ的正弦函数；Cφ表示角度φ的余弦函数，其它的表示方法与文[6]类似。

2 基于目标函数优化方法求解舱临界倾覆角

结合(1)、(2)、(5)、(6)式可以得到包含9个未知量(Hi,θ,φ,φ,i=1, 2 … 6)和6个方程的非线性方程组，在这种情况下解一般不是唯一的，需要通过优化分析的方法从中选择一组最佳解，因此需要定义优化的准则，建立优化分析的目标函数。

本文的目的是寻找在指定位置处满足舱静力平衡条件的舱最大倾覆角，即：

θ=θmax，

(7)

为了保证函数的连续性及良好的可导性，目标函数用下列式子表示：

θ.

(8)

钢索是柔性的，不能承载压力，于是有一个最小力，同时其拉力也不能无限大，值的选取根据实际设计方案而定，设定索力的上下限为

Hmin≤Hi≤Hmax.

(9)

当馈源舱的倾角超过90°即可认为馈源舱已倾覆，方位角的范围为0到360°，根据文[6]，馈源舱自旋角基本在0°，在试验中发现模型舱的自旋角很小，不超过15°，因此本文中的约束范围为0到15°。

当采用目标函数优化方法求解方程组时，原来的9个未知量就变成了优化变量，(8)式就变成了对优化变量的强制约束，同时考虑(1)、(2)式以及3个姿态角的范围，总约束如下：

(10)

通过罚函数法，构建用于求解的无约束目标函数如下：

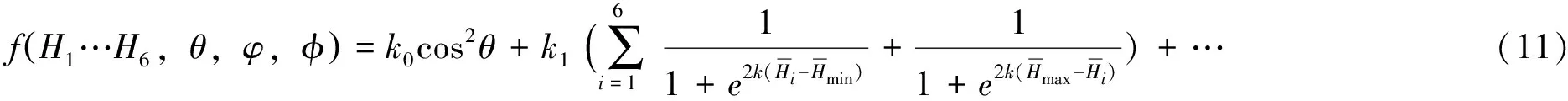
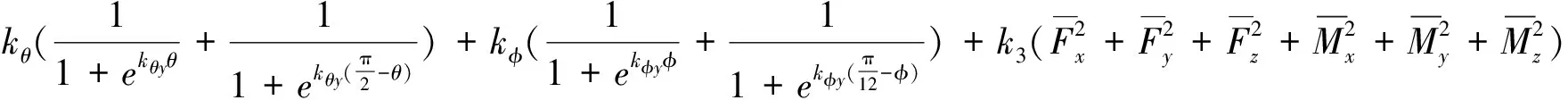
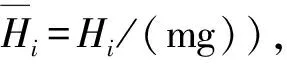
对于(11)式的最小值优化可通过牛顿迭代法求解。在迭代求解过程中需要不断地计算一阶导数(Jacobi矩阵)及二阶导数(Hessian矩阵)，为了判断程序是否结束，在每次计算中需要比较函数值的差值是否小于给定的精度σ，用下式表示：

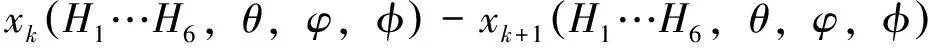
(12)

其中下标k表示第k步迭代。对应有9个未知量的方程，对应的图形很复杂，要寻找全局的最小值，初始值的选择至关重要，首先利用网格法寻找满足条件的解[7]，选择倾角最大的那一组解作为牛顿迭代法初始值，选定初始值后为了更快地收敛，在步长的选择方面通过linesearch方法确定[8-9]，判断是否满足步长选择条件的公式：

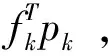
(13)

上式是为了保证方程f朝着减小的方向选择步长，因此式中c很小，在本试验中令c=10-4，为第k步待求的步长，计算步长的具体步骤为：

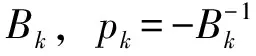
(2)计算θ(α0)，如果满足(13)式，αk=α0，结束，否则进入步骤(3)；

(3)在步骤(2)的基础上利用已知的3个信息θ(α0)、θ(0)、θ＇(0)，构建一个平方插值多项式来拟合θ(αk)，其表达式如下：

＇(0)a1+θ(0)，

(14)

令该方程式取最小值的解为

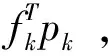
(15)

计算θ(αk1)=f(xk+αk1pk)，判断是否满足(13)式，如果满足则令αk=αk1，程序结束，否则转到步骤(4)；

(4)构建一个3次插值多项式，使其最小化的值计算方式如下：

(16)

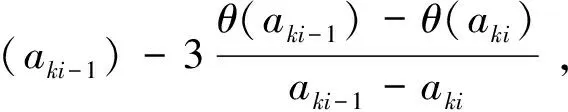
(17)

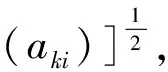
(18)

计算θ(aki+1)=f(xk+aki+1pk)，判断是否满足(13)式，如果满足则令αk=aki+1，程序结束，否则一直进行步骤(4)，直到满足(13)式。

在计算过程中为了保证每次计算的αk与上次计算的αk-1相比变化不大，因此做了如下的规定：如果αk≫0.5αk-1，令αk=0.5αk-1；如果αk≪0.1αk-1，令αk=0.1αk-1。在得到步长的基础上对函数f的最优化求解，步骤如下：

(1)输入系统基本参数；

(2)判断重心ZZ是否小于给定值，例如10mm，如果成立进行步骤(3)，否则进行步骤(6)；

(3)输入初值x0，通过计算旋转矩阵R, a, h, Tan,tanβ等，确定fk，通过linesearch法计算步长ak，如果有合适的ak，转到步骤(4)，否则转到步骤(5)；

(4)判断解向量增量是否满足判断条件，即‖Δ{x}‖，满足进入步骤(5)，否则用计算得到的xk代替xk-1，继续步骤(3)；

(5)重心ZZ加1，转到步骤(2)；

(6)差值计算重心连续变化过程中对应倾角的值；

(7)结束。

流程图如图5。

3 舱索系统模型优化结果及试验

如图6，在室内搭建一个3m尺度的实验模型，主要模拟FAST原型的舱-索系统。试验模型的主要参数按照相似原则进行选定，如表1。

3m模型与FAST原型之间遵循几何相似比：1/200，质量相似比1∶178570；其中质量相似比是根据几何相似比与单位长度索自重比得到，模型主要参数均由此两个相似比参数导出。

为了充分体现馈源舱在整个馈源焦面上最大倾角，本文选择了如图2的3个白圈位置，分别为馈源焦面的最低点或中心点①，边缘点③和中间点位置②，根据相似原则，3m模型的索力范围为0到2.1N，模型馈源舱重心移动到铰接点平面以上10mm时，图2(a)中δ，相当于原型馈源舱重心在铰接点平面以上2m，已基本达到原型馈源舱在铰接点平面以上的最大高度，因此只考虑重心最大增加到10mm。重心位置从0开始，理论计算结果如图7。

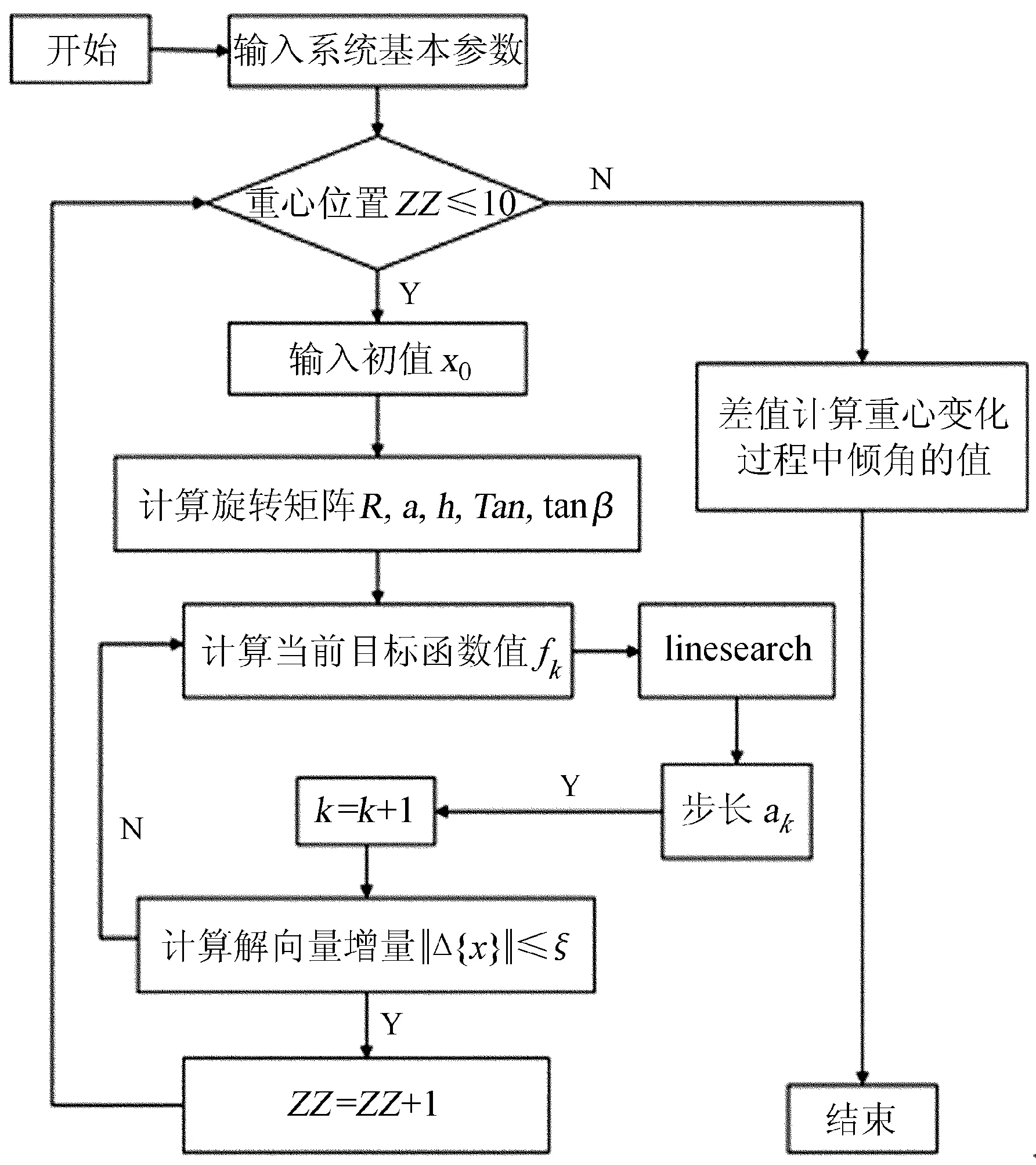
图5 优化求解流程图

Fig.5Aflowchartoftheroutinetofindtheoptimalsolutionofacriticaltiltforoverturningofthefocuscabin

表1 3 m模型及FAST原型分析中所采用的主要几何和力学参数

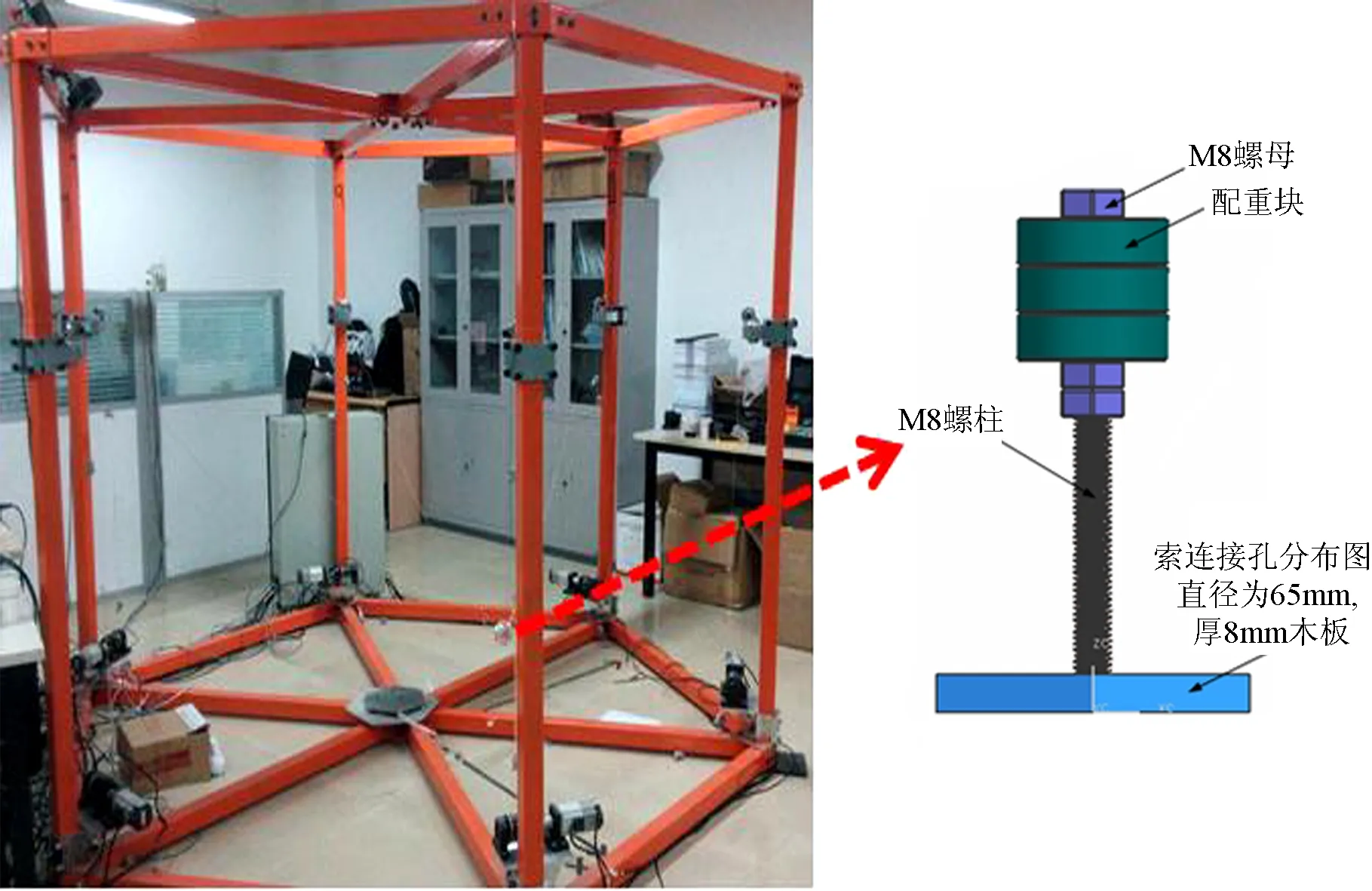
图6 3 m模型全景图及模型舱示意图

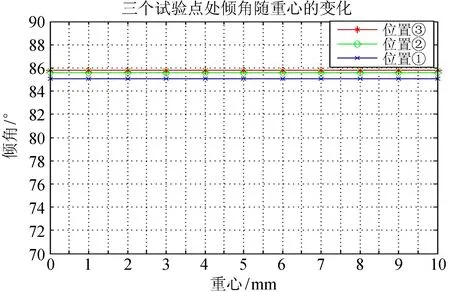
图7 选定位置处最大倾角随重心的变化图

图7表示选定的位置处，随着重心的改变，在索力允许的范围内，模型舱所能达到的最大角度，由图可知，最大倾角从位置①到③呈现逐渐增大的趋势，其最大倾角在位置①处收敛到85.04°左右，位置②处收敛到85.68°，位置③处收敛到85.78°，且重心在0到10 mm范围内的改变对所处位置的最大倾角几乎没有影响。

图8中3张图片均采用双纵坐标轴表示，横坐标表示重心的改变，上图纵轴表示索力，中图的纵轴表示角度，图8显示的重心改变过程中索力及姿态角相对于重心为0时对应量的改变量，通过对索力及姿态角随重心变化的分析可知，当重心变化时，索力、方位角及自旋角变化明显，馈源舱的最大倾角不随重心的改变而变化是由于钢索的索力及另外两个姿态角的变化综合导致的。

通过计算选定位置处倾角最大的情况下的6根索长，调节3 m模型中所对应的钢丝绳的长度，通过测量模型舱的高度差的方式，得到了3 m模型在选定的位置处，如图2，模型舱重心在铰接点以上10 mm时的倾角，结果如表2，试验测得在3个位置处的馈源舱倾角(重心位置10 mm)实测值与理论值的对比。

3 m模型试验所得数据接近理论计算的最大倾角，且索力均在给定的范围内，说明理论分析结果是可靠的。误差的出现可能因为模型索舱锚节点处为固性链接以及钢丝绳本身的刚度较大引起，如图9。

最后分析了FAST原型中馈源舱在整个馈源焦面上的临界倾覆角，索力上下限分别为0及40 t，计算中使用的参数如表1，得到的结果如图10(a)，其中10(b)是FAST原型基于索力优化的结果[5]。

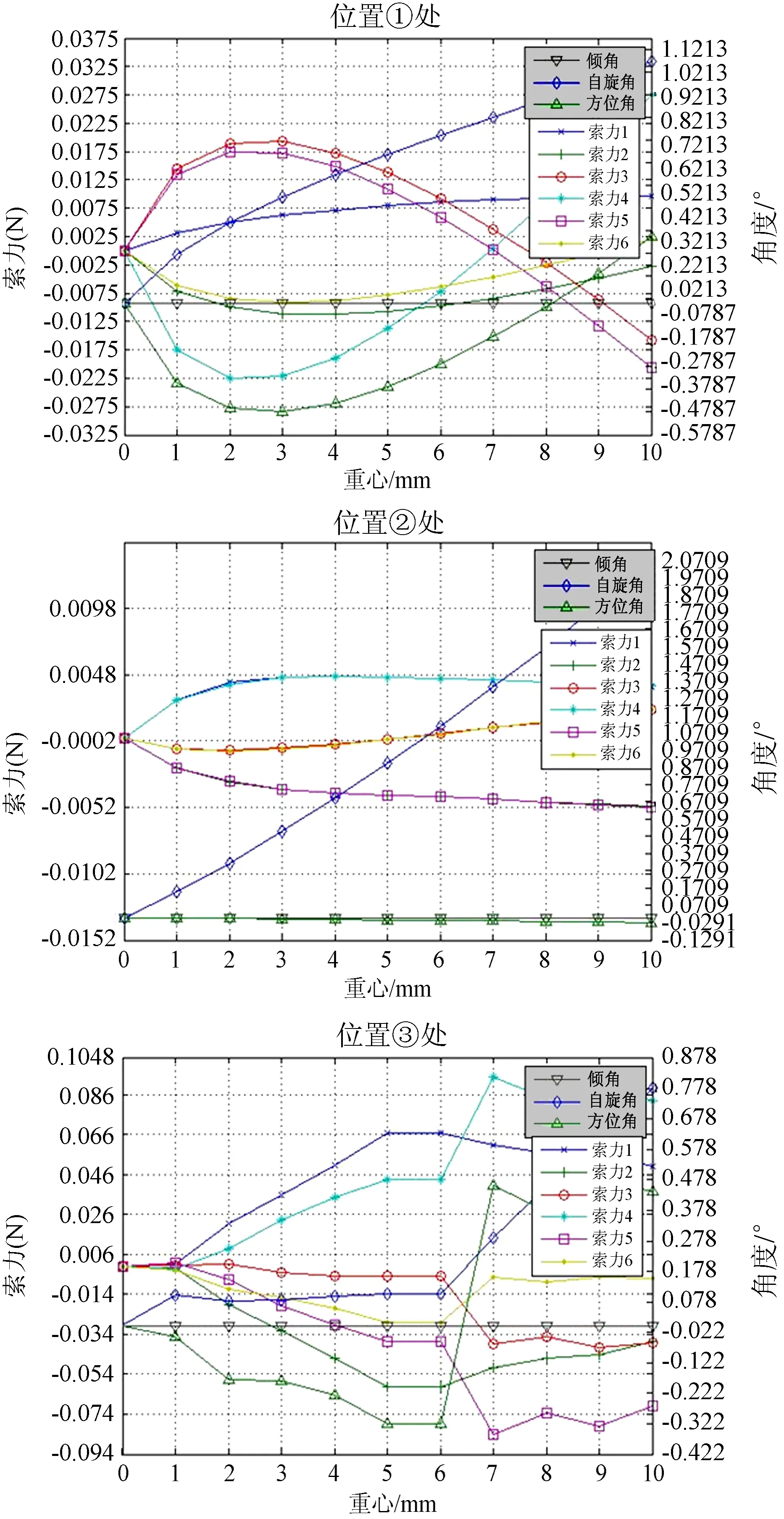
图8 选定位置处索力及姿态角随重心的变化图

Fig.8 Variations of cable tensions and attitude angles with the center of gravity (COG) at the chosen locations

表2 3个试验点处的馈源舱倾角

从图10(a)可知，在整个馈源焦面上，馈源舱在索力允许的范围内的最大倾角呈现从最低点到馈源焦面边缘逐渐增大的趋势，其计算结果最小值出现在最低点，为84.95°，最大值出现在焦面边缘，为86.84°，与馈源舱倾角在焦面最低点处最小，边缘处最大的趋势相符。

从图10(b)可知，FAST在执行天文观测任务的过程中馈源舱倾角在0～17.5°范围，远小于舱倾覆角，因而馈源舱在整个馈源焦面上是安全的。

图9 位置③处重心为10 mm时3 m模型舱的倾角图

图10 FAST原型中馈源舱临界倾覆角在馈源焦面的分布

4 结 论

本文通过理论分析和模型试验对FAST馈源舱在馈源焦面上运行过程中的临界倾覆角及是否存在倾覆的可能性进行了研究。通过模型试验验证了理论分析结果的可靠性。

理论分析结果表明，馈源舱临界倾覆角的最小值出现在焦面最低点，为84.95°，最大值出现在焦面边缘为86.84°，馈源舱在实际运行过程中最大倾角约为17.5°，远远小于最大倾角的最小值，因此馈源舱在整个馈源焦面上运行过程中是安全的。馈源舱重心在一定范围内的改变对舱临界倾覆角几乎没有影响。

[1] Nan Rendong. Five hundred meter aperture spherical radio telescope (FAST) [J]. Science in China: Series G Physics, Mechanics & Astronomy, 2006, 49(2): 129-148.

[2] 孙欣, 段宝岩. 巨型柔性Stewart平台解空间、工作空间的研究及悬索张力的优化分析[J]. 机械工程学报, 2002, 38(2): 16-21. Sun Xin, DuanBaoyan. Study on solution space, working space and cable tension’s optimized analysis for huge flexible stewart platform[J]. Chinese Journal of Mechanical Engineering, 2002, 38(2): 16-21.

[3] 姚蕊, 唐晓强, 李铁民, 等. 大型射电望远镜馈源定位3T索牵引并联机构分析与设计[J]. 机械工程学报, 2007, 43(11): 105-109. Yao Rui, Tang Xiaoqiang, Li Tiemin, et al. Analysis and design of 3T cable-driven parallel manipulator for the feedback’s orientation of the large radio telescope [J]. Chinese Journal of Mechanical Engineering, 2007, 43(11): 105-109.

[4] 黄亮, 朱文白, 唐晓强, 等. 大射电望远镜索牵引并联机构索力优化分析[J]. 天文研究与技术——国家天文台台刊, 2010, 7(3): 268-276. Huang Liang, Zhu Wenbai, Tang Xiaoqiang, et al. Optimization of cable tensions of a cable-driven parallel manipulator for a large radio telescope[J]. Astronomical Research & Technology——Publications of National Astronomical Observatories of China, 2010, 7(3): 268-276.

[5] Li Hui, Nan Rendong, Kärcher Hans. Working space analysis and optimization of the main positioning system of FAST cabin suspension, in ground-based and airborne telescopes II[C]// Proceedings of SPIE. 2008.

[6] 李辉, 朱文白, 潘高峰. 基于索力优化的FAST柔索牵引并联机构的静力学分析[J]. 工程力学, 2011, 28(4): 185-207. Li Hui, ZhuWenbai, Pan Gaofeng. Equilibrium analysis of FAST rope-drive parallel manipulator based on rope force optimization[J]. Engineering Mechanics, 2011, 28(4): 185-207.

[7] 朱永生. 实验物理中的概率和统计[M]. 北京: 科学出版社, 2006: 512-513.

[8] Dennis J E, Schnabel R B. Numerical methods for unconstrained optimization and nonlinear equations[M]. Englewood Cliffs: Prentice-Hall, 1983.

[9] Nocedal J, Wright S J. Numerical Optimization[M]. New York: Springer-Verlag, 1999: 35-61.

A Theoretical Analysis and an Experimental Study of Overturning of the Focus Cabin of the FAST

Li Mingzhe1,2,3, Li Hui2,3

(1. College of Science, Guizhou University, Guiyang 550025, China; 2. National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012, China; 3. Key Laboratory of Radio Astronomy, Chinese Academy of Sciences, Beijing 100012, China, Email: limingzhe@nao.cas.cn)

The focus cabin of the FAST (Five-hundred meter Aperture Spherical radio Telescope) is supported and driven by six parallel flexible steel cables, so that it is suspended in the air and traces a spherical focal surface. As a result, the orientation of the focus cabin is adaptive to the variable spatial position of the focus cabin. The adaptation nevertheless raises the risk of overturning of the focus cabin during its motion. In this paper we first theoretically analyze the mechanics of overturning of the focus cabin and present verification of the analysis through experiments on a 3m scaled model of the FAST focus cabin-cable system. We then establish an object function of optimization of the critical tilt of overturning of the focus cabin by taking the static-equilibrium equations and the limits on cable tensions/cabin orientations as the constraint conditions. We employ the Newton Iteration Method to obtain optimal solutions of the critical tilts using the function. We have also evaluated and tested the effect of the location of the center of gravity (COG) of the focus cabin on the critical tilts. Our test results show accurate consistency with our theoretical analysis. We finally present the calculation results of the critical tilts of the actual focus cabin at all its accessible locations on the focal surface. The results show that a cabin tilt under a normal circumstance is much less than the critical tilt of overturning of the focus cabin. This means the focus cabin is normally safe.

FAST telescope; Focus cabin; Overturning; Static force analysis; Model test

国家自然科学基金 (10973023, 11103046, 211311001) 资助.

2015-03-06；修定日期：2015-04-13

李铭哲，男，硕士. 研究方向：索牵引并联机构动力学. Email: limingzhe@nao cas cn

O312; TH751; TP242

A

1672-7673(2015)04-0424-09

CN 53-1189/P ISSN 1672-7673