减隔震支座对不同墩高桥梁地震反应的影响

陈 光 王晓伟 叶爱君

(同济大学土木工程防灾国家重点实验室，上海200092)

1 引言

我国是地震多发的国家，地震活动频率高、强度大、震源浅、分布广，特别是近些年，中西部山区地震频发［1］。桥梁作为生命线系统工程中的关键组成部分，在抗震救灾中起到了至关重要的作用。对于地震作用，传统的结构设计采用的是结构抗震，即主要考虑为结构提供抵抗地震作用的能力。但在某些情况下，依靠结构自身来抵抗地震作用显得非常困难，需要付出很大的经济代价，因此需要寻求更为有效的抗震手段。近年来，在震害调查及破坏机理研究的基础上［2］，基于桥梁抗震设计的结构控制技术开始在我国桥梁工程界得到日益重视，逐步开展了桥梁减隔震设计及研究工作，其中，采用减隔震支座对桥梁进行抗震设计是一种广泛采用的手段［3］，通过延长结构的周期达到减小地震反应的目的。目前，《城市桥梁抗震设计规范》［4］中规定减隔震支座适用的范围为墩高较小的桥梁，但是实际工程中存在墩高较高的桥梁也使用减隔震支座的情况。

国内外关于减隔震支座对不同墩高桥梁地震反应影响的研究还较少。高亮亮和商耀兆［5］研究了减隔震支座对高墩铁路梁桥减隔震地震反应特性的影响，但是没有考虑到桥墩墩高的变化;张骏和阎贵平［6］研究了不同墩高下减隔震支座对桥梁位移反应的影响，但是未研究结构内力的变化。因此，研究减隔震支座对不同墩高桥梁地震反应的影响是必要的。

本文以一座实际连续梁桥为例，采用SAP2000通用有限元程序，建立数值模型，研究了不同墩高下，减隔震支座对桥梁的自振特性、位移反应以及桥墩内力的影响，并得出相关结论。

2 桥梁结构简介及建模

某一城市快速路高架桥的一联连续梁桥［7］，跨径组合为4 m×29 m，一联总长为116 m，立面布置见图1。桥宽24．3 m，主梁为单箱四室截面;下部结构为带系梁双柱墩，墩高为10 m，墩柱采用实心钢筋混凝土截面，尺寸为1．3 m×1．8 m，墩柱轴线横向间距为5．7 m;矩形承台，11．6 m×7．2 m，高 2．5 m，重 522 t;群桩基础，桩长 40 m，桩数12根，桩径1．0 m，单桩配筋率1．0%，横断面布置如图2所示。

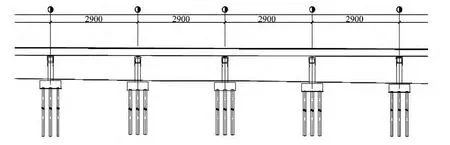
图1 桥梁立面图(单位:mm)Fig．1 Vertical section of the bridge(unit:mm)

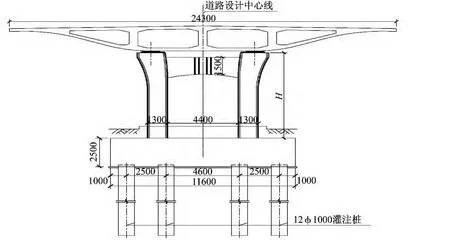
图2 桥梁断面图(单位:mm)Fig．2 Cross section of the bridge(unit:mm)

上部结构、立柱、基础分别采用 C50、C40、C35混凝土。上部结构和二期恒载等总质量为6 498 t，中墩两墩墩顶反力之和为15 403 kN，次边墩两个墩顶反力为17 636 kN，边墩两墩墩顶反力为6 502 kN。

对该连续梁桥，分别采用如下两种设计方案进行对比分析:

(1)常规体系:每个墩上均采用盆式支座，纵桥向中间桥墩支座为固定型，其余均为滑动型;横桥向一侧为固定型，另一侧为滑动型。

(2)减隔震体系:每个墩上均采用摩擦摆式支座。

2．1 全桥动力分析模型

根据结构设计方案，利用SAP2000程序建立空间三维结构动力有限元分析模型，其中主梁、横梁、桥墩模拟为空间梁单元;承台模拟为质点，二期恒载模拟为线分布质量;桩基础采用六弹簧模拟;支座采用连续单元模拟，活动方向用双线性模型模拟。全桥的动力分析模型如图3所示。

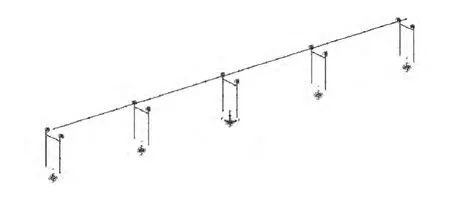
图3 全桥动力分析模型Fig．3 Dynamic analysis model of bridge

2．2 支座恢复力模型的选取

2．2．1 常规体系

常规体系活动支座的摩擦作用效应可采用双线性理想弹塑性弹簧单元模拟，其恢复力模型见图 4，并应符合下列要求［8］。

活动支座临界滑动摩擦力Fmax:

初始刚度:

式中，μd为滑动摩擦系数，取值为0．02;W为支座所承担的上部结构重力;xy为活动盆式支座屈服位移，取 0．003 m。

图4 活动盆式支座恢复力模型Fig．4 Restoring force model of movable GPZ

2．2．2 减隔震体系

摩擦摆式减隔震支座的恢复力模型如图5所示，屈后刚度为

等效刚度为

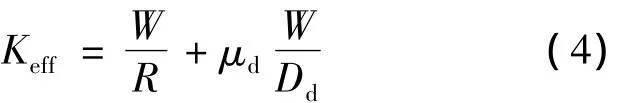
等效阻尼比为

式中，W为恒载作用下支座竖向反力;R为滑动曲面的半径，为5 m;Dd为支座设计水平位移;μd为滑动摩擦系数，为0．02。

图5 摩擦摆式支座恢复力模型Fig．5 Restoring force model of friction pendulum bearing

2．3 地震动输入

桥梁所在场地的设计基本地震加速度峰值为0．15 g，抗震设防烈度为7度，地震分区第2区，场地类型为Ⅲ类场地，则反应谱特征周期为0．55 s。

按照《公规》［1］，该桥梁类别为 B 类，E2地震下调整系数 Ci为 1．3，场地系数 Cs为1．3，阻尼调整系数Cd为1．0。水平设计反应谱方程为

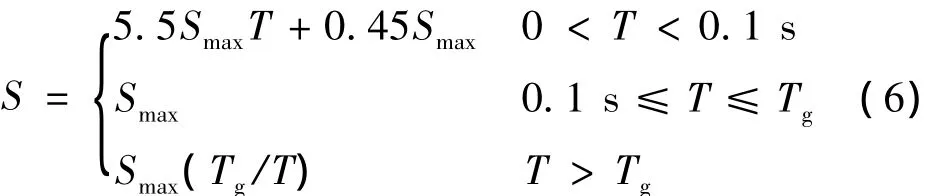
式中，水平设计加速度反应谱最大值 Smax=2．25CiCsCdA，A为地震加速度峰值。

图6所示为水平向加速度反应谱曲线。

图6 阻尼比为5%的加速度反应谱曲线Fig．6 Acceleration response spectrum in damping ratio of 5%

对于E2设防概率水准，根据反应谱拟合了7条地震波。图7为其中的一条地震加速度时程曲线。

为了了解这组地震加速度时程的频谱成分，将这7条时程转换为对应的反应谱，并与设计反应谱进行比较，由图8可知，E2地震加速度时程和设计反应谱的频谱成分吻合较好。图9为其对应的位移反应谱。

由于采用摩擦摆式支座的减隔震桥梁在纵桥向和横桥向的减震机理是一致的，本文仅给出纵向地震输入下的计算结果，同时不考虑竖向地震作用的输入。

图7 人工地震加速度时程图Fig．7 Artificial earthquake acceleration time history

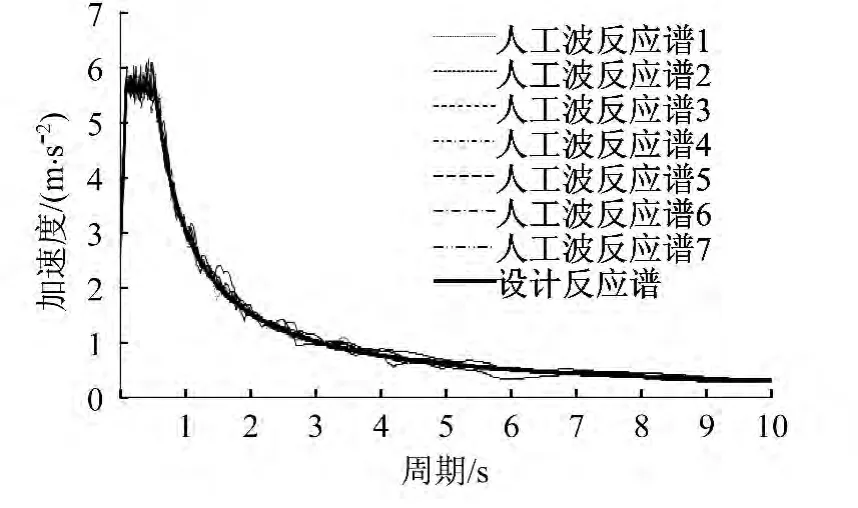
图8 设计反应谱与人工加速度时程反应谱Fig．8 Designed response spectrum and acceleration response spectrum obtained by artificial earthquake acceleration time history

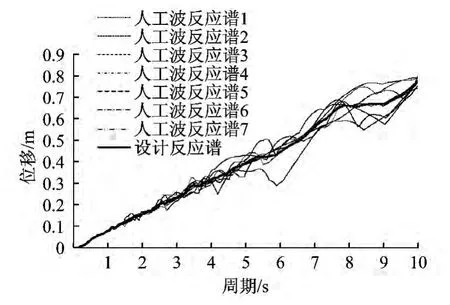
图9 阻尼比为5%的位移反应谱Fig．9 Displacement response spectrum in damping ratio of 5%

3 地震反应分析

根据SAP2000计算所得的结果进行地震反应分析，本文从桥墩内力、桥梁位移反应以及桥梁的自振特性三个方面分别进行了比较分析。

3．1 桥墩内力比较

图10为减隔震体系以及常规体系的墩底剪力随墩高的变化规律，从图中可以得出，在墩高较小时，常规体系的剪力值比减隔震体系的剪力值大得多，减隔震支座起到了良好的减震性能;随着墩高的增加，两种体系的墩底剪力均减小。在墩高较高时，常规体系与减隔震体系剪力值相差不大，此时，减隔震支座减震性能已不明显。另外，对于墩底剪力，常规体系滑动墩与减隔震体系的变化规律类似。

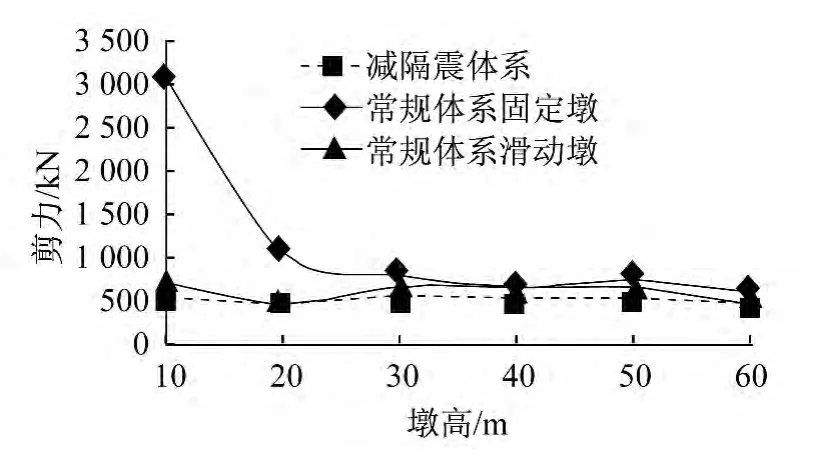
图10 墩底剪力值随墩高的变化规律Fig．10 Regulation that the pounding bottom shear changes with the height of pier

表1为减隔震支座对不同墩高桥梁墩底剪力的影响，分析表中数据也同样可以得出，在墩高较小时，减隔震体系有着良好的减震性能，而墩高较高时，减震效果不明显。

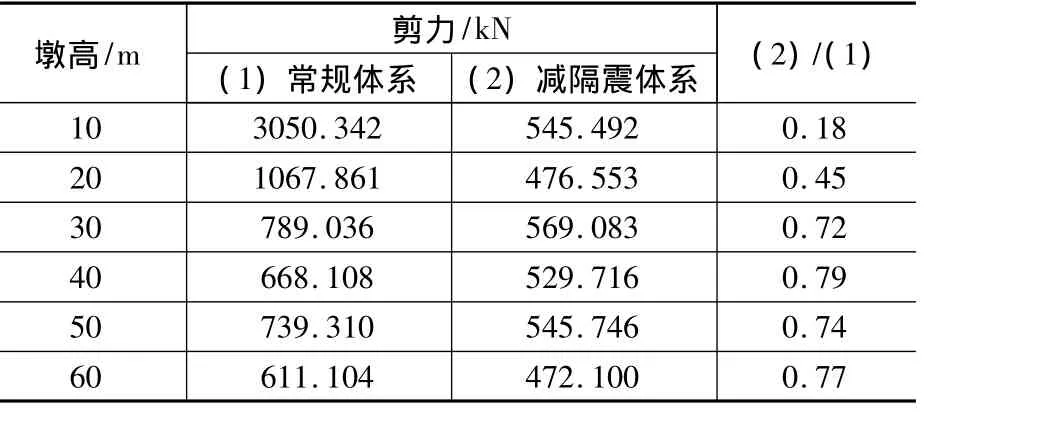
表1 减隔震支座对不同墩高桥梁墩底剪力的影响Table 1 Effects of isolation bearing on the pounding bottom shear of bridge with different pier height

图11为两种体系墩底弯矩随墩高的变化规律，从图中可得，在墩高较小时，减隔震体系的弯矩值明显小于常规体系固定墩的弯矩值，而在墩高较高时，两者差距很小。

表2为减隔震支座对不同墩高桥梁墩底弯矩的影响，分析表中的数据，在墩高较小时，减隔震体系墩底弯矩与常规体系墩底弯矩的比值很小，表明减隔震支座起到了良好的减震效果;而在墩高较高时，比值很大，此时减隔震支座起到的减震效果不明显。

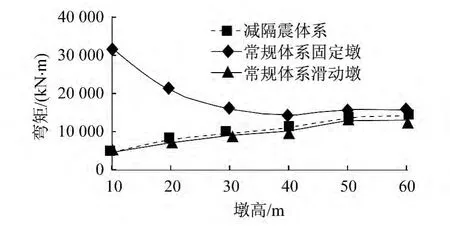
图11 墩底弯矩值随墩高的变化规律Fig．11 Uariation of that the pounding bottom bending moment the change with of the height of pier

表2 减隔震支座对不同墩高桥梁墩底弯矩的影响Table 2 Effects of isolation bearing on the pounding bottom bending moment of bridge with different pier height

3．2 桥梁位移反应分析

从位移反应谱(图9)可得，在10 s的周期内，位移随着周期的增大而增大。图12为减隔震体系下桥梁各关键部位的位移反应随墩高的变化规律。随墩高的增加，上部结构位移以及墩顶位移都增加，与位移反应谱相一致，这主要是由于随墩高的增加，结构的刚度减小，变形增大。

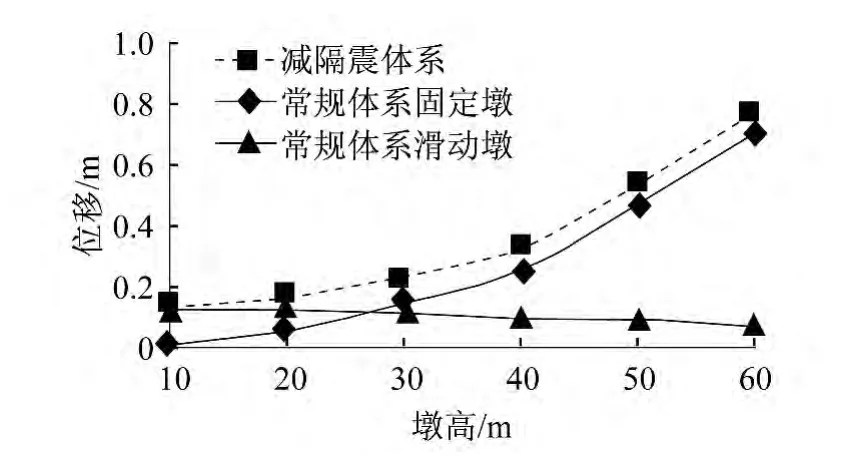
图12 墩高对减隔震体系桥墩以及上部结构纵向地震反应的影响Fig．12 Effects of the height of pier on longitudinal seismic response of isolation bearing bridge's pier and superstructure

表3为减隔震支座变形占上部结构位移的比例，从表中可以得出，在墩高较小时，支座变形是上部结构位移的控制因素，当墩高较高时，支座变形占桥梁上部结构位移的百分比很小，支座变形对上部结构位移的贡献很小。此时上部结构变形主要由墩身贡献。

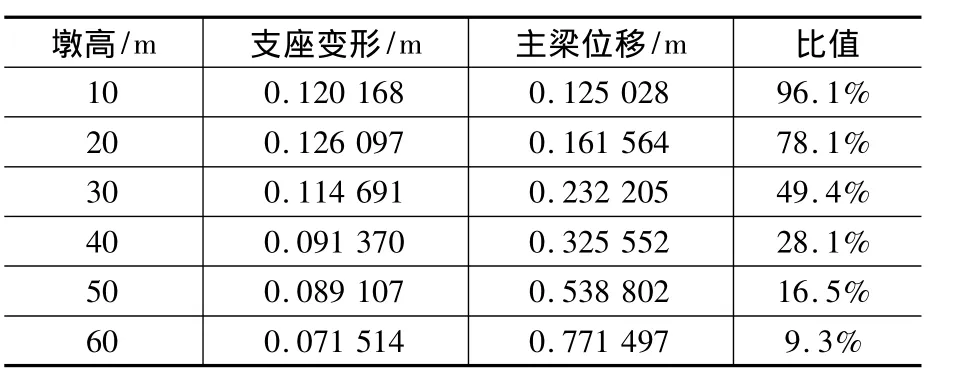
表3 减隔震支座变形占上部结构位移百分比Table 3 Ratio of isolation bearing deformation and the displacement of superstructure

图13为10 m、40 m墩高支座的滞回曲线。从图中可得，10 m墩高时支座耗能比40 m墩高大，结合图12，由于随墩高的增加，支座变形减小，支座耗能减小，所以在墩高较高时减隔震支座的减震耗能作用降低，此时，使用减隔震支座减震效果不明显。

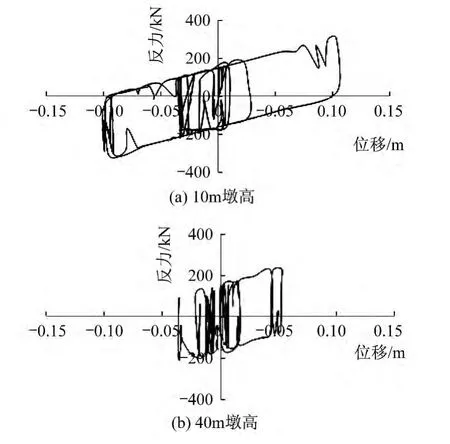
图13 减隔震支座滞回曲线Fig．13 Hysteretic curve of isolation bearings

图14 为两种体系上部结构位移随墩高的变化规律。从图中可以得出，两种情况的位移值都随着墩高的增加而增加，与位移反应谱相一致。再对比两条曲线可知，在10 m墩高时，减隔震体系上部结构位移为常规体系上部结构位移的1．6倍，而在墩高比较高时，两种体系上部结构位移相差不大，结合图13分析，在墩高较高时，减隔震支座变形小，耗能差，支座提供的柔性降低，这也是在高墩时减隔震支座运用较少的原因。

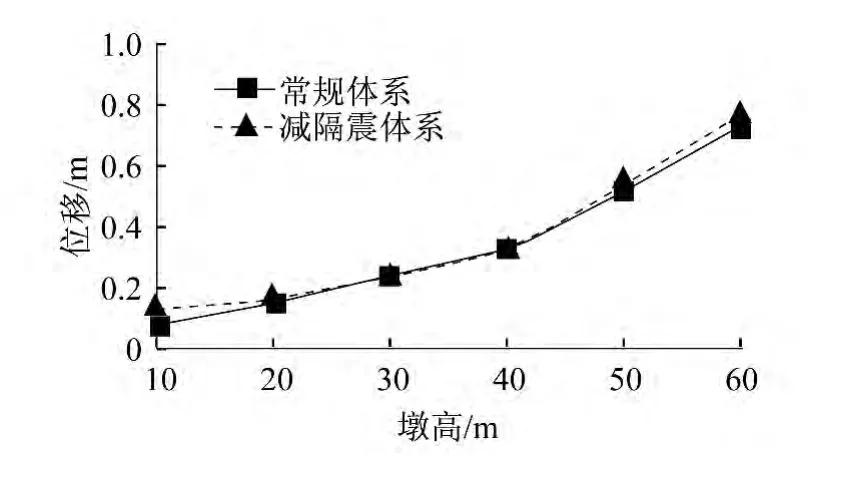
图14 上部结构位移随墩高的变化规律Fig．14 Uariation of the displacement ofsuperstructure with the change of the height of pier

从以上的对比中可以得出，在墩高较小时，减隔震支座对桥梁有着良好的减震性能，当墩高比较高时，减震效果不明显。主要是由于墩高较高时，结构的自振周期较长，此时设置减隔震支座对延长结构周期的效果不明显，因此减震效果亦不佳。

3．3 桥梁自振动特性分析

常规体系桥梁的等效基本周期可按下式进行计算:

式中，Mt为换算质点质量;δ为在顺桥向作用于支座顶面或上部结构质心上单位水平力在该处引起的水平位移。

与一般计算常规体系基本周期的方法不同的是，本文在计算时，滑动墩的刚度采用的是等效刚度，计算方法与减隔震体系相同。

减隔震体系桥梁等效周期按下式计算:

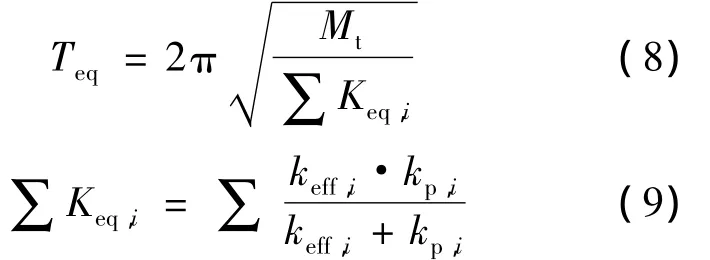
式中，Keq，i为第i桥墩、桥台与其上的减隔震装置等效刚度串联后的组合刚度值;kp，i为第i桥墩、桥台的抗推刚度;keff，i为第i桥墩、桥台上减隔震装置的等效刚度。

对于减隔震体系桥梁，其自振特性计算简图见图15。

按照以上的计算方法，求得减隔震体系以及常规体系的等效基本周期，见表4。

从表4中可以得到，两种体系的周期都随着墩高的增加而增加，这说明墩高的增加使得桥梁结构变柔、整体刚度变小、自振周期变长。同时对比两组数据，在墩高较小时，采用减隔震支座能起到较好地延长结构自振周期的作用，但是墩高较高时，采用减隔震支座对延长周期的效果不明显，这是由于在墩高较小时，减隔震体系支座变形大，等效刚度小，起到了延长结构周期的作用，而墩高较高时则相反，采用减隔震支座难以达到延长结构周期、减小结构内力的目的。另一方面，当墩高过高时，结构变柔，结构本身的自振周期较长，通过设置减隔震支座来延长结构周期的方法作用不大。

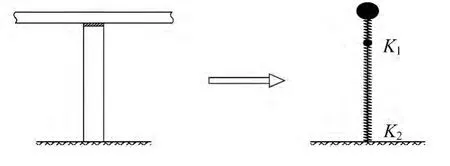
图15 自振特性计算简图Fig．15 Calculation diagram of self vibration characteristic

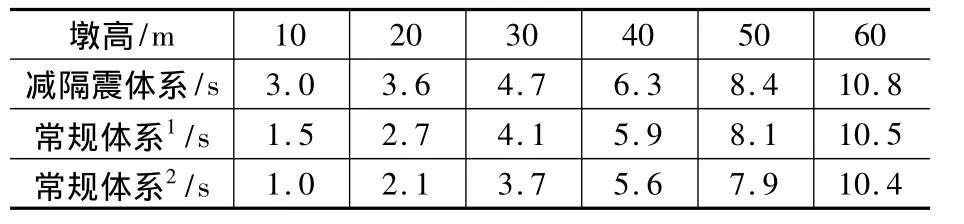
表4 等效基本周期随墩高的变化规律Table 4 Variation of that equivalent fundamental period with the change of the height of pier

4 结论

由上述的分析结果可以得出如下结论:

(1)随着墩高的增加，减隔震体系以及常规体系周期均增加，当墩高较小时，减隔震支座对于延长结构周期有显著效果，而墩高较高时效果不明显。

(2)对于减隔震体系，在墩高较小时，桥梁的上部结构位移主要由支座变形提供，而在墩高较高时，支座变形很小，此时上部结构位移主要由桥墩墩身位移贡献。

(3)在墩高较小时，减隔震支座对于桥墩墩底的剪力、弯矩的减小量都较大，即减震效果比较显著，而在墩高比较高时，减隔震支座起到的减震效果并不明显。

(4)实际抗震设计中，对于墩高较高的情况，减隔震支座的运用应谨慎对待。

［1］ 胡聿贤．地震工程学［M］．北京:地震出版社，2006．Hu Yuxian．Earthquake engineering［M］．Beijing:Earthquake Press，2006．(in Chinese)

［2］ 王东升，郭迅．汶川大地震公路桥梁震害初步调查［J］．地震工程与工程振动，2009，29(3):84-94．Wang Dongsheng，GuoXun．Damagetohighway bridges during Wenchuan Earthquake［J］．Journal of Earthquake Engineering and Engineering Vibration，2009，29(3):84-94．(in Chinese)

［3］ 范立础，卓卫东．桥梁延性抗震设计［M］．北京:人民交通出版社，2001．Fan Lichu，Zhuo Weidong．Seismic design and retrofit of bridges［M］．Beijing:China Communications Press，2001．(in Chinese)

［4］ 中华人民共和国住房和城乡建设部．CJJ 166—2011城市桥梁抗震设计规范［S］．北京:人民交通出版社，2011．Ministry of Housing and Urban-Rural Development of People’s Republic of China．CJJ 166—2011 Code for seismic design of urban bridge［S］．Beijing:China Communications Press，2011．(in Chinese)

［5］ 高亮亮，商耀兆．铅芯橡胶支座高墩铁路简支梁桥减隔震特性的研究［J］．铁道建筑，2008(5):7-10．Gao Liangliang，Shang Yaozhao．Study on seismic absorption and isolation of the high pier railway simply supported girder bridge by lead-rubber bearing［J］．Railway Engineering，2008(5):7-10．(in Chinese)

［6］ 张骏，阎贵平．减隔震支座对梁式桥抗震性能的影响［J］．中国公路学报，2002，15(1):38-43．Zhang Jun，Yan Guiping．Effects of isolation bearing on anti—seismic performance of RC beam bridge［J］．China Journal of Highway and Transport，2002，15．(1):38-43．(in Chinese)

［7］ 叶爱君，管仲国．桥梁抗震［M］．北京:人民交通出版社，2011．Ye Aijun，Guan Zhongguo．Seismic design for highway bridge［M］．Beijing:China Communications Press，2011．(in Chinese)

［8］ 中华人民共和国交通运输部．JTG/T B02—01—2008公路桥梁抗震设计细则［S］．北京:人民交通出版社，2008．Ministry of Transport of People’s Republic of China．JTG/T B02—01—2008 Guidelines for seismic design of highway bridge［S］．Beijing:China Communications Press，2008．(in Chinese)