轴心受压构件弹性扭转的失稳分析

刘卫东

（大连海洋大学应用技术学院，辽宁大连 1 1 6 3 0 0）

轴心受压构件弹性扭转的失稳分析

刘卫东

（大连海洋大学应用技术学院，辽宁大连 1 1 6 3 0 0）

钢结构中一般采用非圆截面构件，此类构件的扭转与圆形截面构件不同，前者扭转后的截面不再保持平面，而要发生翘曲，即截面上各点产生轴向位移。如果能够自由翘曲，外扭矩将全部由剪应力抵抗，这类扭转称为自由扭转、纯扭转或均匀扭转；如果截面不能自由翘曲，则外扭矩由剪应力和翘曲扭矩共同抵抗，这类扭转称为约束扭转或非均匀扭转。

轴心受压；弹性扭转；屈曲荷载；残余应力

0.引言

一般双轴对称截面的轴心受压构件，可能绕截面的两个对称轴发生弯曲失稳；但是，对于抗扭刚度弱的轴心受压构件还可能发生绕纵轴的扭转失稳。钢结构中一般采用非圆截面构件，此类构件的扭转与圆形截面构件不同，前者扭转后的截面不再保持平面，而要发生翘曲，即截面上各点产生轴向位移。如果能够自由翘曲，外扭矩将全部由剪应力抵抗，这类扭转称为自由扭转、纯扭转或均匀扭转；如果截面不能自由翘曲，则外扭矩由剪应力和翘曲扭矩共同抵抗，这类扭转称为约束扭转或非均匀扭转。

1.轴心受压构件弹性扭转屈曲荷载

图-1a所示双轴对称工形截面轴心受压构件，两端夹支或称为简支。所谓夹支是指构件的端部截面只能绕两个主轴x、y自由转动，而不能绕纵轴z扭转，并且端部截面的翼缘可以自由翘曲。用平衡法求扭转屈曲荷载，需研究图-1b所示构件绕纵轴有微小扭转角时的受力条件。在距原点为z处截面的扭转角为φ，z＋d z处截面的扭转角为φ＋dφ。图-1e所示在微段d z内的任一纤维DE因构件扭转而位移至D′E″，D′E″与竖直线D′E′的夹角为α，水平面内E″与截面剪心S相距ρ。由于夹角α很小，则有

由于纤维有倾斜，作用于纤维上端E″处的力σd A在水平面内产生分力σ′d A，绕剪心S形成扭矩ρσ′d A。

由图-1f知，纤维上端的水平分力为

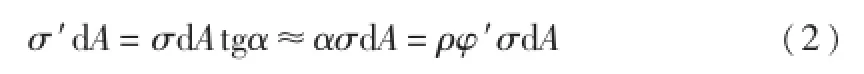
构件扭转时，全截面形成的约束扭矩为

离原点距离为z处截面的扭矩平衡方程为Mz=Mst+ Mw，即

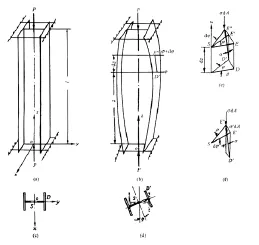
图-1 轴心受压构件的扭转变形

由边界条件φ（0）=0，得到C2＋C3＝0；Bw=-EIwφ″（0）＝0，即φ″（0）＝0，得到C2=0，则有C3=0；由φ（l）=0，得到C1sin kl=0，因C1≠0，只有sin kl=0，即（kl）min=π。则得弹性扭转屈曲临界荷载

相应的临界应力

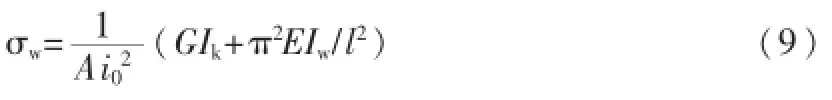
也可以将式（9）表达成同弯曲屈曲相仿的形式

式中λw称为扭转屈曲长细比，具体表达式为

式中lw=μwl称为扭转计算长度，μw为扭转计算长度系数，其取值与弯曲屈曲时的取值相同。

2.残余应力对扭转屈曲荷载的影响

发生约束扭转时，有纵向残余应力σrs的轴心受压构件，由于纤维倾斜，σrsdA在水平面内同样产生水平分力σrsdAρφ′，计算约束扭矩Mz时应考虑在内，即

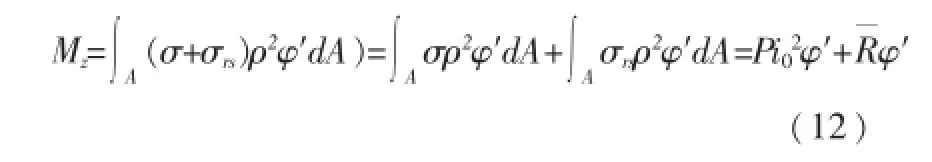
考虑残余应力影响的约束扭转的扭矩平衡方程为

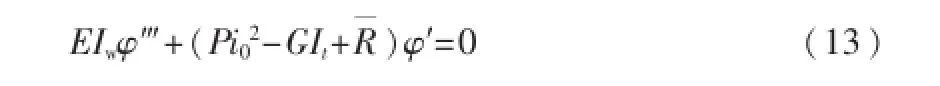
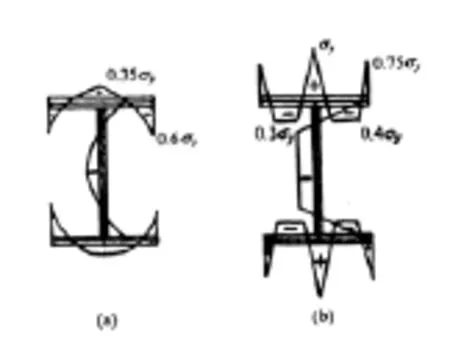
图-2 焊接工形截面残余应力分布

从上式中可以看出，残余应力对轴心受压构件扭转屈曲的影响取决于的大小和正负号。值与截面残余应力的分布情况有关，对翼缘为轧制边的焊接工形截面，残余应力分布如图-2a所示是正值，将降低P w值；而当翼缘为火焰切割边时，残余应力分布见图-2b，为负，将提高P w值。

3.结语

上述讨论是如何确定弹性扭转屈曲荷载及残余应力对屈曲荷载的影响。自由扭转构件各截面的翘曲相同，因此，构件的纵向纤维不产生轴向应变，截面上没有正应力而只有扭转引起的剪应力。纵向纤维不发生弯曲，即翼缘和腹板的纵向纤维保持直线，上下翼缘相互仅扭转了一个角度φ（扭转角）。对于抗扭刚度低的双轴对称截面轴心受压构件（如十字形截面构件），可能在轴向压力尚未达到欧拉临界力之前，构件就发生绕纵轴的扭转失稳。

[1]魏明忠．钢结构[M].武汉：武汉理工大学出版社，2002.

[2]孙训方．材料力学[M]．北京：高等教育出版社，2001.

[3]苏德利.杆件在复杂内力作用下的强度分析[J]．沈阳师范大学学报，2010，（4）.

[4]刘文顺.弹性介质上变截面压杆的稳定分析[J]．焦作大学学报，2007，（1）.

（责任编辑 陈永康）

TU311.2

A

1 008－72 57（201 5）01－0 090－02

2014－07－25

刘卫东（1964－），男，辽宁大连人，大连海洋大学应用技术学院副教授，研究方向：结构力学。