基于FHPN的道路交叉口交通流信号实时控制优化研究

赵进超， 孙建召

(1.郑州轻工业学院 计算机与通信工程学院， 郑州 450002;2.河南经贸职业学院 信息管理系， 郑州 450000;3.中南大学 信息科学与工程学院， 长沙 410083)



赵进超1*， 孙建召2，3

(1.郑州轻工业学院 计算机与通信工程学院， 郑州 450002;2.河南经贸职业学院 信息管理系， 郑州 450000;3.中南大学 信息科学与工程学院， 长沙 410083)

为了合理控制道路交叉口的交通流，结合模糊时延Petri网、连续Petri网和模糊推理Petri网这3种Petri网的优势构造了模糊混合Petri网，以此来建立一个FHPN模型并把它用于道路交叉口交通流信号实时控制.通过实例仿真分析了FHPN模型的有效性，能够实时控制交叉口的运行情况，最大程度地利用道路资源且大幅度地降低了交叉口的停车次数.

交通信号; 实时控制; Petri网

当前城市汽车数量的增长速度远高于城市的道路建设速度，使得城市道路交通日趋紧张，交通拥堵现象越来越严重，于是提高道路交通的通行能力变的越来越迫切.在城市道路交通网络运行的过程交通流量一般都会有比较明显的高峰和低峰，这就需要有不同的信号配时方案来适应不同的交通状况，随之就出现了智能信号灯控制和实时信号灯控制[1-4]的相关研究.

当前，对信号灯的实时控制的相关研究有：文献[5]基于带抑制弧和使能弧的增广Petri网对交叉口的信号灯进行实时控制，通过采集实时的车流量信息来确定信号灯周期及各相位时长.文献[6]基于模糊逻辑对路口交通信号灯进行实时控制，使用模糊逻辑能够更好的描述交叉口信号控制的定性模型，从而对信号相位变化顺序、信号周期和信号绿灯时间进行定性分析和模糊实时控制.文献[7]基于混合Petri网对城市道路交通网络进行建模和仿真，采用连续Petri网对交叉口车流量进行建模，采用时延Petri网对信号灯相位变化进行建模，结合两种Petri网构造混合Petri网来实现单个交叉口的信号控制.

Petri网特别适合描述系统的顺序、并发、冲突和同步等现象，而交通信号灯控制就是一类典型的顺序、并发和同步系统，于是选用Petri网[8]作为交通信号灯的实时控制建模的工具.本文定义了一类新的Petri网模型，即结合模糊时延Petri网[9]、连续Petri网[10]和模糊推理Petri网[11]等各种Petri网的优势构造了模糊混合Petri网，然后给予该Petri网模型对单个交叉口的信号相序和绿灯时间进行实时控制.

1 信号灯控制

信号灯控制道路交叉口的车辆通行是保证城市道路交通安全有序运行的保障，关于信号灯控制主要给出5个概念：路段、周期、相位、绿信比和排队长度[12].以中国车辆靠右行驶的简单路网来解释以上5个概念.在图1中，连接两个交叉口之间的道路称为路段.在图2中，描述的信号灯为四相位的信号灯.周期是指交叉口所有流向都有一次绿灯通行的所有信号灯状态.相位是指某个流向的绿灯通行的信号灯状态， 图2中相位1为东西直行，相位2为东西左转，相位3为南北直行，相位3为南北左转，这里不考虑右转的控制.所有相位时长之和为周期时长.绿信比是指某各相位的绿灯时长占周期时长的比值.排队长度是指车辆在红灯时在交叉口前排队一直到变为绿灯时车辆的总排队长度.

图1 两个交叉口的城市道路Fig.1 City road with Two intersections

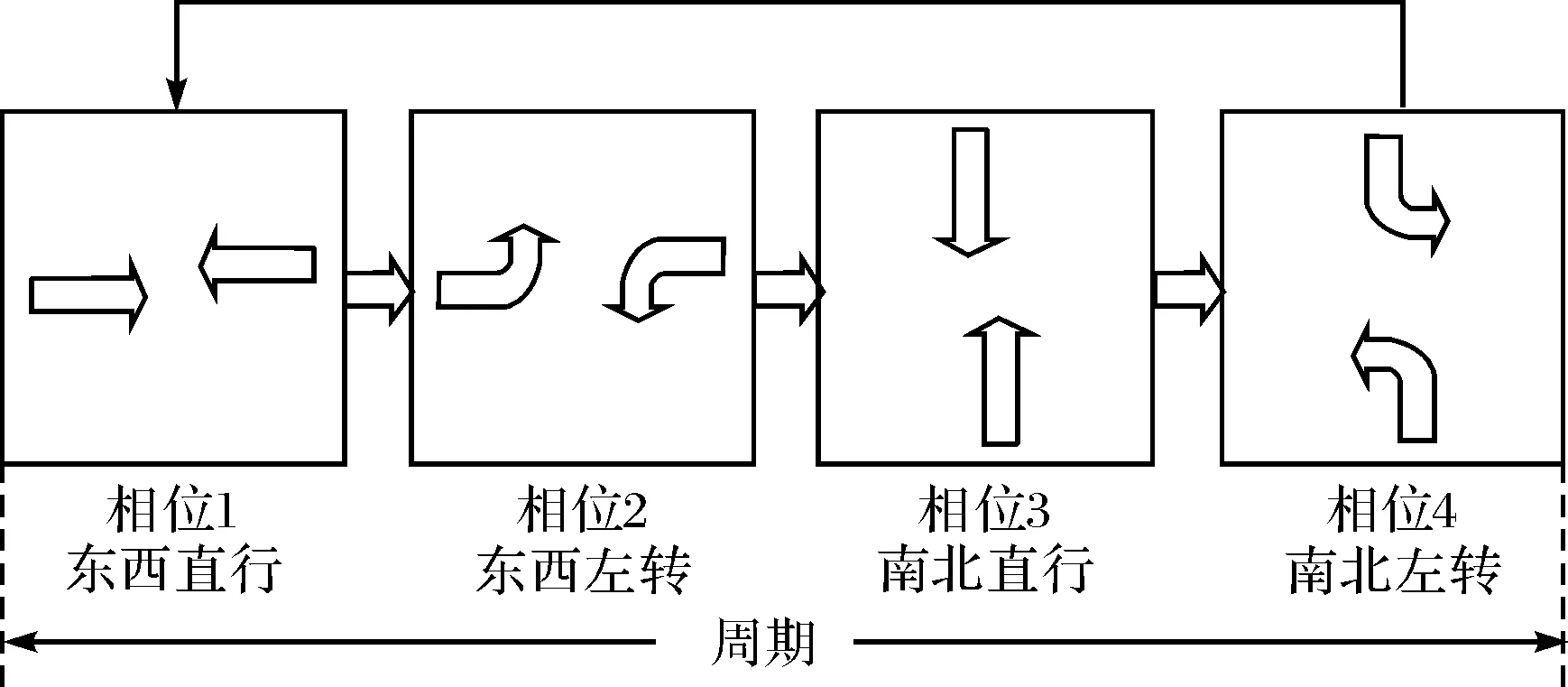
图2 交叉口信号灯相位和周期Fig.2 Phase and cycle of intersection signal

2 模糊混合Petri网

本文以图2所示的四相位的单交叉口为例，构造模糊混合Petri网，其他复杂的单交叉口构造方法类似.

定义1模糊混合Petri网(Fuzzy Hybrid Petri Net， FHPN)模糊混合Petri网是一个八元组

FHPN={P，T，A，DT，PP，PC，R，M0}，

其中，(1)P=Pd∪Pc，Pd是离散库所的集合，Pc是连续库所的集合，Pd∩Pc=∅，离散库所Pd可分为两种库所子集合，即相位标识库所集合Pp和绿灯时间库所集合Pg，Pp∩Pg=∅；

(2)T=Td∪Ti∪Tr，Td是模糊延时变迁的集合，Ti为瞬时变迁的集合，Tr为模糊推理变迁的集合，Td∩Ti∩Tr=∅；

(3)A⊆(P×T)∪(T×P)为输出弧和输入弧的集合；

(4)DT:〈Pp，Td〉→[α，β]为库所Pp和变迁Td到正整数区间[α，β]的映射函数，α，β∈N+且Pp∈•Td；

(5)PP:Pp→(a，b，c，d)为库所Pp到向量(a，b，c，d)的映射函数，a，b，c，d∈{-1，0，1}；

(6)PC:Pc→(w，x，y，z)为库所Pg到正实数向量(w，x，y，z)的映射函数，w，x，y，z∈R+；

(7)PG:Pg→g为库所Pc到正实数g的映射函数，g∈R+；

(8)R为托肯的集合，r∈R的取值由映射函数PP，PC和PG确定；

(9)M0为初始标识，表示系统的初始状态.

定义2模糊延时变迁td的使能与触发规则

模糊延时变迁td∈Td使能，当且仅当：∀p∈I(td)∩Pd，∃r∈M(p).其中，I(td)为变迁td的输入库所，M(p)为库所p的状态标识.

模糊延时变迁td∈Td的触发规则为：如果∀p∈I(td)∩Pd，∃r∈M(p)，∀p'∈O(td)∩Pd，那么M(p)→M(p)/{r}，M(p')→M(p')∪{r}.其中，/表示从库所标识中去除.

定义3瞬时变迁ti的使能与触发规则

瞬时变迁ti∈Ti使能，当且仅当∀p∈I(ti)∩Pd，∃r∈M(p).

瞬时变迁ti∈Ti的触发规则为：如果∀p∈I(ti)∩Pd，∃r∈M(p)，∀p'∈O(ti)∩Pd，那么M(p)→M(p)/{r}，M(p')→M(p')∪{r}；

如果∀p∈I(ti)∩Pd，∃r∈M(p)，∃p'∈O(ti)∩Pc，那么M(p)→M(p)，M(p')→M(p')Δ{r}.其中，Δ表示连续库所p'中的标识与托肯r的一种运算，形成库所p'中的新标识.

定义4模糊推理变迁tr的使能与触发规则模糊推理变迁tr∈Tr使能，当且仅当：∀p∈I(tr)，∃r∈M(p).

模糊延时变迁td∈Td的触发规则为：如果∀p∈I(tr)，∃r∈M(p)，∀p'∈O(tr)，那么对∀p∈Pc有M(p)→M(p)，对∀p∈Pd有M(p)→M(p)/{r}，M(p')→M(p')∪{r}.

3 本文信号灯控制FHPN模型

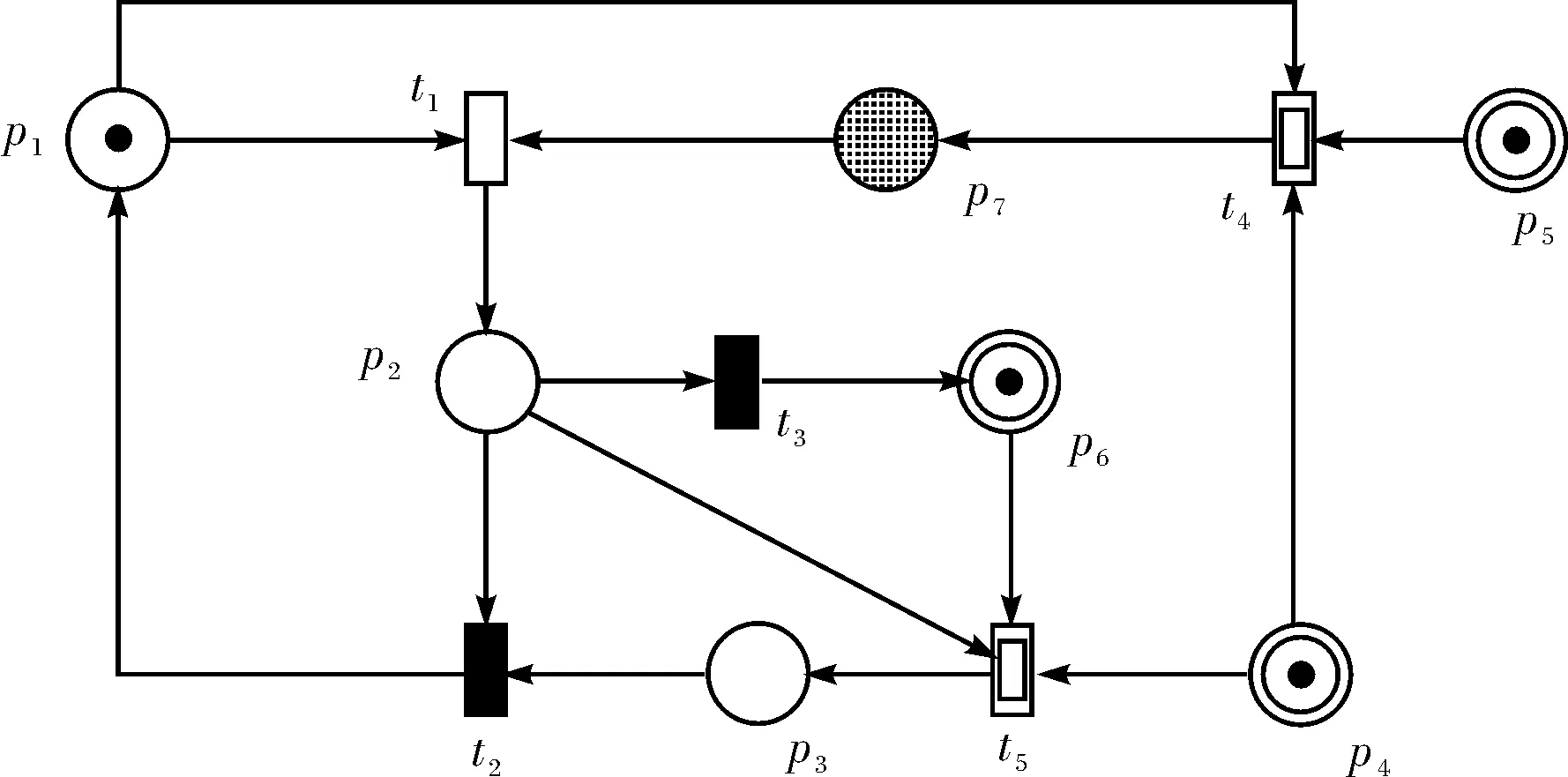
图3 信号灯控制的FHPN模型Fig.3 FHPN model of signal

基于以上的定义先构建单交叉口四相位的信号灯控制FHPN模型，如图3所示.库所和变迁的含义如表1和表2所示.其中：q11表示东西直行排队长度，q12表示东西左转排队长度，q21表示南北直行排队长度，q22表示南北左转排队长度，单位为米(m)；f11表示东西直行的车流量，f12表示东西左转的车流量，f21表示南北直行的车流量，f22表示南北左转的车流量，单位为每15 min车辆数(pcu)；r11表示东西直行红灯时间，r12表示东西左转红灯时间，r21表示南北直行红灯时间，r22表示南北左转红灯时间，单位为秒(s).

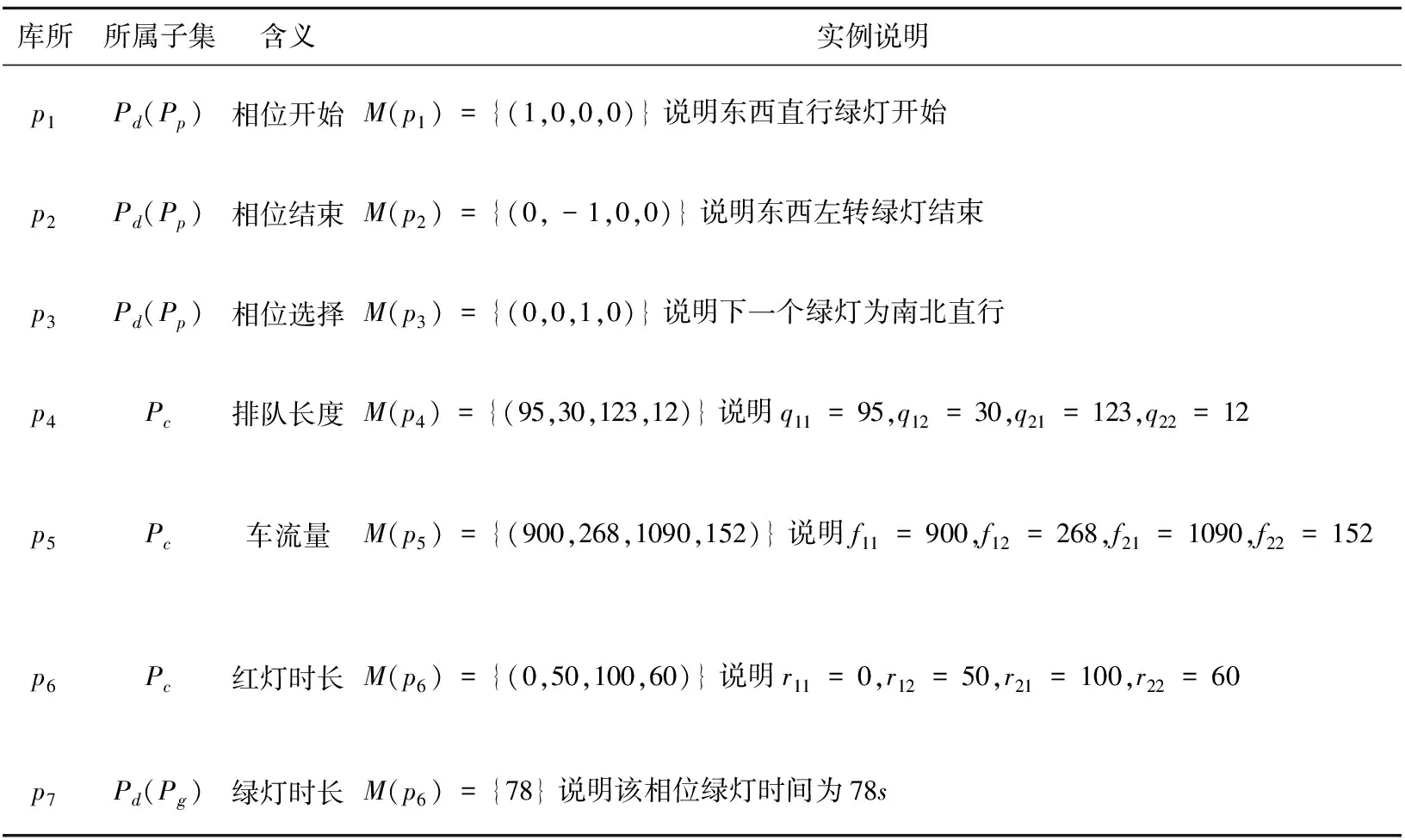
表1 FHPN中库所的含义

表2 FHPN中变迁的含义

连续库所p4和p5中的托肯r的取值由交叉口附近的传感器实时的获取；连续库所p6中时间托肯r随时间更新，同时变迁t3的触发会改变时间托肯r的取值，把结束相位的红灯时间改为0.推理变迁t4和t5的触发，其前置库所中连续库所中托肯的取值不改变，而离散库所的托肯会消失；其他变迁的触发都是使的前置库所的托肯转移到后置库所中，但取值会根据不同的规则来确定.

4 本文FHPN模型分析

本文中的下一个相位的确定是实时的，即相位1、相位2、相位3和相位4四个相位不一定是以固定的顺序发生的，可能出现1-3-4-1-2的情况，故暂时不讨论信号周期.这里主要分析各相位绿灯时间的确定和相序的确定.

4.1 实时确定相位绿灯时长

相位绿灯时长的确定有推理变迁t4来确定，前置库所包括连续库所和离散库所，离散库所确定要推理的绿灯时长为哪一个相位，连续库所排队长度和车流量来确定绿灯时长.若前置离散库所p1的标识为M(p1)={(0，0，1，0)}，则所要计算绿灯时长的相位为相位3，即南北直行绿灯时长，然后提取连续库所p4中相位3的排队长度q21和连续库所p5中相位3的车流量f21，再通过一个模糊推理Petri网来推理所需要的绿灯时长，最后得到后置库所p7的绿灯时长，即确定了相位3的绿灯时长.

交叉口的具体位置和特性决定不同的模糊推理过程，首先构造模糊控制器[13]，输入量为排队长度Q和交通流量F，排队长度以米为单位，隶属函数如图4所示，交通流量以每小时车辆数位单位，隶属函数如图5所示；输出量为绿灯时间T，以秒为单位，隶属函数如图6所示.模糊推理是根据相关交通智能方法及经验得到，模糊推理规则如表3所示，推理结论的隶属度为推理条件隶属度的最小值，去模糊化方法采用加权平均隶属度法则来计算.因篇幅有限，这里不给出模糊推理的详细过程.

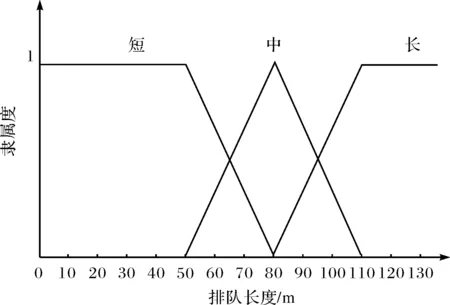
图4 排队长度Q的隶属函数Fig.4 The membership function of queue length Q

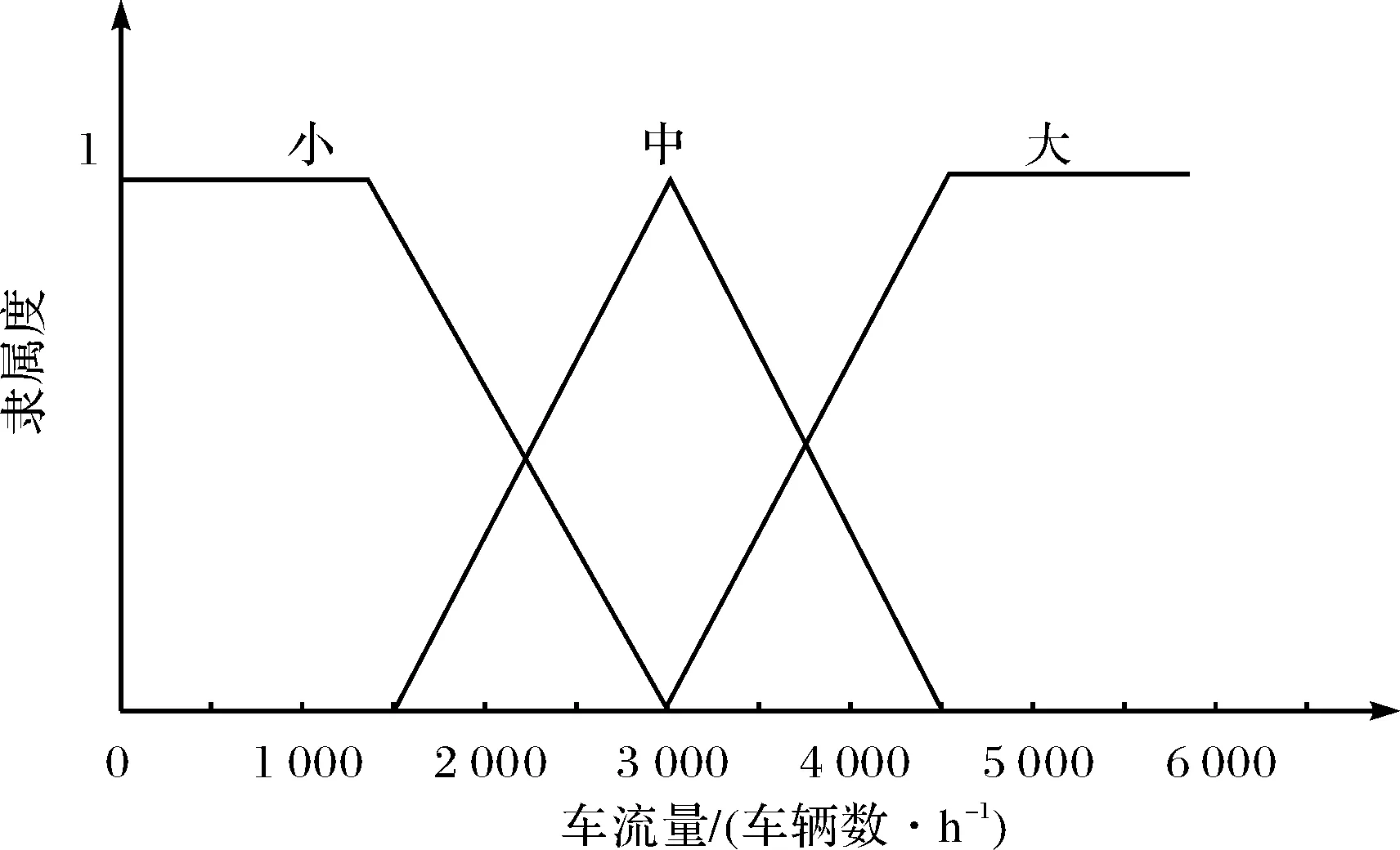
图5 车流量F的隶属函数Fig.5 The membership function of traffic flow F

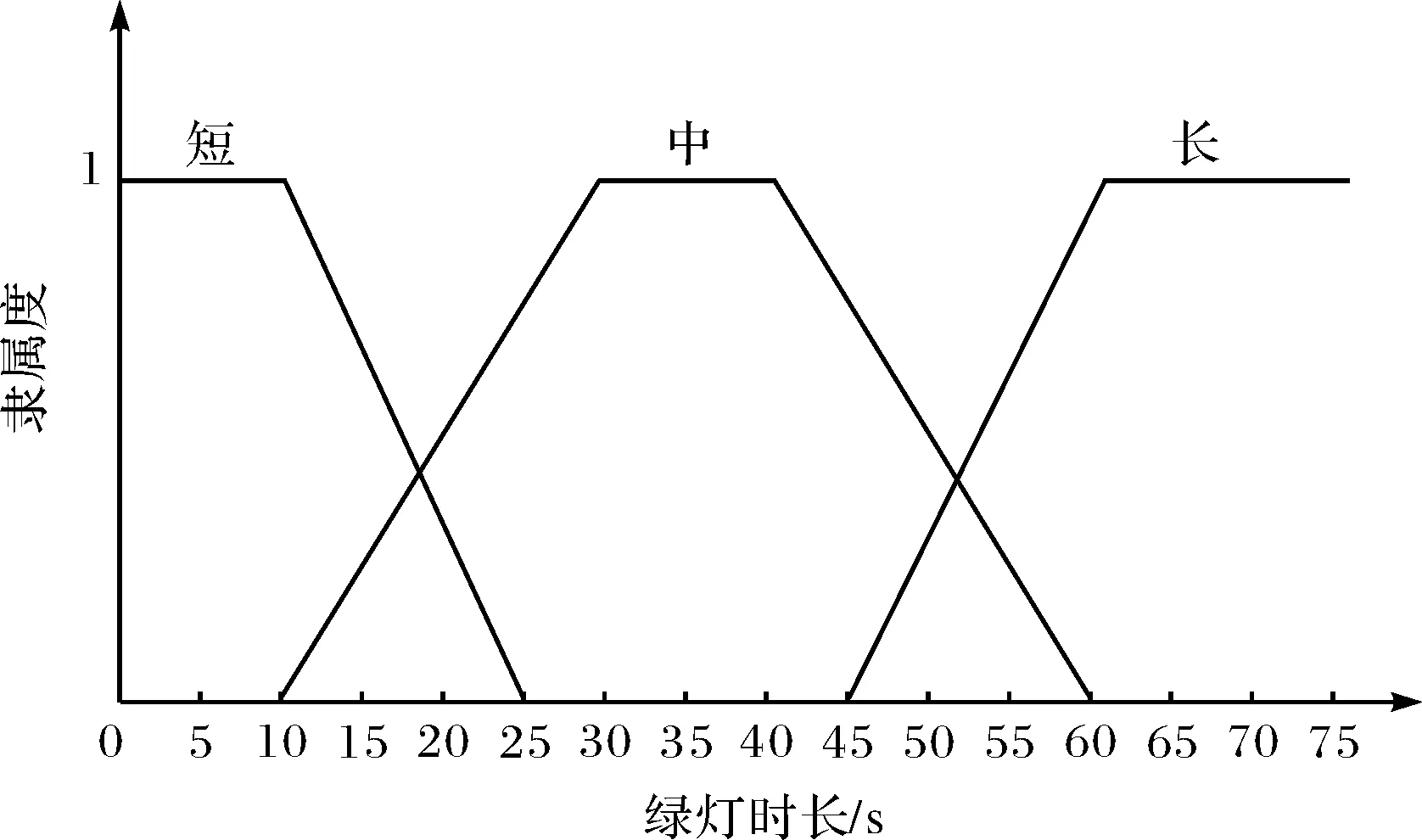
图6 绿灯时长T的隶属函数Fig.6 The membership function of green light time T

表3 模糊推理规则

基于以上的模糊控制器，构造的模糊推理Petri网如图7所示，其库所和变迁的含义如表4所示，其中，库所p3-p11中的托肯值为隶属度，库所p1中的托肯值为排队长度值，库所p3中的托肯值为交通流量值，库所p12为中的托肯值为绿灯时间值.

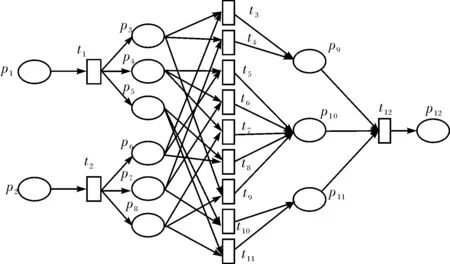
图7 模糊推理Petri 网Fig.7 Fuzzy reasoning petri net

表4 模糊推理Petri网中库所和变迁的含义

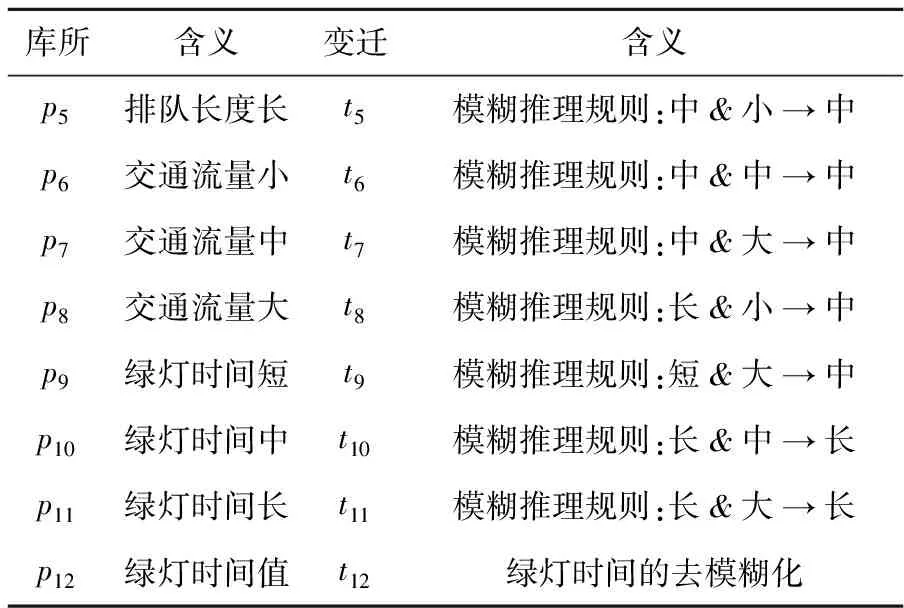
续表4

以上模糊推理Petri网的推理过程详细说明了FHPN中变迁t4的触发过程，即相位的开始的瞬间确定了绿灯时长，由于变迁t4的触发使得库所p7中产生托肯值η，此时延迟变迁t1可触发，因映射函数DT使得延迟变迁对应一个正整数区间[α，β]，α表示前置库所描述的相位最短绿灯时间，β表示前置库所描述的相位最长的绿灯时间.延迟变迁t1的触发由η和[α，β]共同决定，如果α<μ<β，则t1在延迟η秒触发，使得库所p2中产生托肯，表示该相位绿灯结束，即将进入下一相位；如果η≤α，则t1在延迟α秒触发，使得该相位结束；如果η≥β，则t1在延迟β秒触发，使得该相位结束.

4.2 实时确定下一个相位

交叉口信号灯的实时控制不仅要考虑当前相位的绿灯时长，尽量保证通行的车辆有较少的停车次数，同时要考虑所有方向的车辆的延迟，于是在考虑相位变换的时候，本文采用可变相序的实时控制.

在图7中，如果库所p2中含有托肯，且M(p2)={(0，-1，0，0)}，说明相位2结束，下一个相位可为相位1，相位3或者相位4.首先库所p2中的托肯使得瞬时变迁t3触发，使得连续库所p6中的托肯值发生变化，例如：瞬时变迁t3触发前：

M(p2)={(0，-1，0，0)}，

M(p6)={(50，165，115，15)}，

则触发后：

M(p2)={(0，-1，0，0)}，

M(p6)={(50，0，115，15)}.

此时模糊推理变迁t5触发，假设触发前M(p4)={(130，5，120，30)}，通过模糊推理Petri网可以得到变迁t5触发后库所p3的标识为M(p3)={(0，0，1，0)}，即说明下一个绿灯相位为相位3.

模糊推理变迁t5的触发过程是3个模糊推理Petri网的结果，其结构与图7中的模糊推理Petri网类似，因篇幅有限这里不做详细说明.因M(p2)={(0，-1，0，0)}，则只需考虑相位1、相位3和相位4这3个相位的红灯时长和排队长度，推理的结果为下一个相位选择的可能性，如果推理结果分别为0.8，0.9和0.1，选择最大的可能性，于是选择相位3，即为标识M(p4)={(0，0，1，0)}的推理过程.这里强调了下一个相位的选择需要考虑两个因素，第一是红灯时长，第二是排队长度.

离散库所p2的标识M(p2)={(0，-1，0，0)}和离散库所p3的标识M(p3)={(0，0，1，0)}使得瞬时变迁t2触发，触发后离散库所p1的标识M(p2)={(0，0，1，0)}，即所选择的下一个相位为相位3.

5 实例仿真

基于信号灯实时控制的模糊混合Petri网模型，设置相关参数进行仿真分析.这里设置东西直行的绿灯时间的最大值和最小值为90s和40s，东西左转的绿灯时间的最大值和最小值为30s和15s，南北直行的绿灯时间的最大值和最小值为80s和30s，南北左转的绿灯时间的最大值和最小值为25s和10s.在此给出3个交通流量2 000pcu/h、3 500pcu/h和5 000pcu/h进行对比分析，以15min的总停车次数作为指标来评价模糊混合Petri网的信号灯控制方法，对比的控制方法为传统定时控制方法和传统实时控制方法，结果如表5所示.

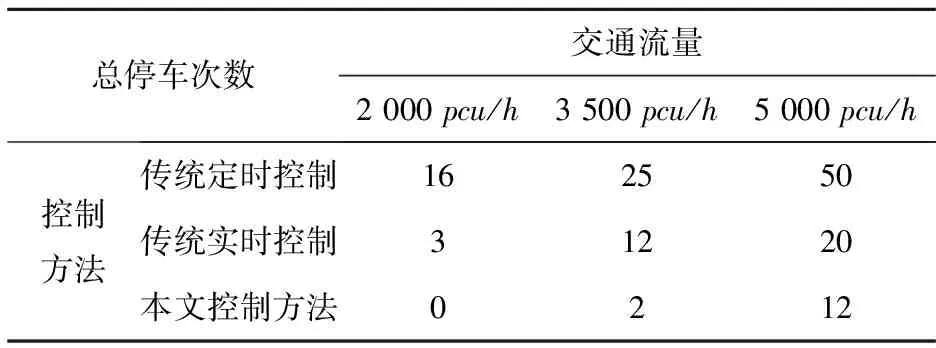
表5 仿真结果

6 结束语

本文主要的研究是提出了模糊混合Petri网，结合了模糊时延Petri网、连续Petri网和模糊推理Petri网等各种Petri网的优势，以交通信号灯实时控制为例子，实时控制绿灯的时间和相序的变化.通过实例仿真分析了FHPN模型的有效性，能够实时控制交叉口的运行情况，最大程度的利用道路资源且大幅度的降低了交叉口的停车次数.下一步的主要研究工作就是加入模糊时间Petri网[14-15]对主干道单流向的信号灯联合控制以及更复杂的交叉口信号灯联合控制进行建模和分析.

[1] 朱铭琳， 赵润林. 单点交通信号控制系统的优化设计与仿真[J]. 计算机工程与应用， 2013， 49(10):253-257．

[2] 杨晓辉. 基于PLC的交通信号灯控制系统研究[J]. 中国新技术新产品， 2012， 17(07):38-39．

[3] 师亚娟，朱忠杰. 基于PLC的交通信号灯控制系统创新实验平台的设计与实现[J]. 工业仪表与自动化装置， 2013， 43(02):70-72．

[4] 黄 玲， 刘 培. 基于PLC的十字路口交通信号灯控制[J].硅谷， 2013， 124(4):35-36．

[5] 叶剑虹， 叶 双， 宋 文， 等. 基于增广Petri网的实时交通信号控制系统[J]. 厦门大学学报:自然科学版， 2011， 50(1): 28-32．

[6] 赵 晨， 胡福乔， 施鹏飞. 基于模糊逻辑的路口交通信号控制[J]. 计算机工程， 2003， 29(10): 50-52．

[7] 岳 昊. 基于混合Petri网的城市道路交通网络建模和仿真[D]. 山东: 山东科技大学， 2009．

[8] 袁崇义.Petri网原理与应用[M]. 北京: 电子工业出版社， 2005．

[9] 高 翔， 祝跃飞，卢锦江. 基于双枝模糊逻辑和模糊着色Petri网的攻击模型[J]. 计算机应用研究， 2013， 30(5): 1527-1530．

[10] 朱婷婷，袁 杰. 学习环境模糊Petri网多变量输出模型与计算[J]. 计算机仿真， 2013， 30(5):325-329．

[11] 尹 久，曹华军， 杜彦斌. 基于广义模糊Petri网的陶瓷生产过程能量碳流模型[J]. 系统工程理论与实践， 2013， 33(4):1035-1041．

[12]LiuZ，LiuJ，HanQ.OntheTrafficSignalsHierarchicalFuzzyControlSystems[C]//DuZi-De:The13thAnnualConferenceofSystemEngineeringSociety.Beijing:TsinghuaUniversityPress， 2004:287-299．

[13] 邝先验， 吴翠琴， 许伦辉， 等. 交通信号多相位智能优化控制方法[J]. 计算机工程， 2008， 34(20): 205-207．

[14] 田 钊， 佘 维， 叶阳东. 基于模糊时间知识推理的实时系统冲突研究[J]. 计算机工程， 2011， 37(14): 183-188．

[15] 黄光球，李 艳，王金成. 双枝模糊时间Petri网可修复网络攻击模型[J]. 计算机工程与应用，2011，47(5): 87-91．

Real-time control optimization research on road intersection traffic signal based on FHPN

ZHAO Jinchao1， SUN Jianzhao2，3

(1.School of Computer and Communication Engineering， Zhengzhou University of Light Industry， Zhengzhou 450002;2.Department of Information Management， Henan Vocational College of Economics and Trade， Zhengzhou 450000;3.College of Information Science and Engineering， Central South University， Changsha 410083)

In order to reasonably control the road intersection traffic flow， this paper combined fuzzy-timing Petri net， continuous Petri net and fuzzy-reasoning Petri net to construct fuzzy hybrid Petri nets(FHPN). A FHPN model was proposed to used in Real-time Control Optimization Research on Road Intersection Traffic Signal. The simulation analysis showed the FHPN model was effective and able to control intersection operation in red time， making the best use of road resources and greatly reduce the count of the vehicle stops．

traffic signal; real-time control; Petri net

2014-08-24.

郑州市科技计划项目(131PPTGG411-8)．

1000-1190(2015)03-0373-05

TP391.7

A

*通讯联系人. E-mail: xiangmulunwen@yeah.net．