基于遗传算法的大学生就业信心指数组合预测*

周润娟，蔡金平，胡长新

（安徽工程大学电气工程学院，安徽芜湖241000）

基于遗传算法的大学生就业信心指数组合预测*

周润娟，蔡金平，胡长新

（安徽工程大学电气工程学院，安徽芜湖241000）

大学生的就业信心指数的变化趋势，可作为高校制定学生工作计划、应对当前就业形势压力的参考依据，信心指数预测结果的准确性直接关系到政策制定与实施的效果。在分析自回归、神经网络及灰色系统等单预测模型的优点与不足基础上，提出综合利用各单模型预测信息的组合预测思路，构建基于遗传算法和信息熵求解单模型权重的组合预测模型。预测结果显示，组合预测模型在拟合期的表现与神经网络模型接近，优于其它两种模型；在预测期远超过其它模型的预测效果。组合预测模型的拟合性能和泛化性能优越，预测信息可作为高校制定相关政策时的重要参考依据。

大学生就业;信心指数;组合预测;遗传算法;信息熵

前言

准确掌握大学生就业信心情况，有助于及时把握大学生思想动态，为高校制定人才培养方案和应对就业问题措施，提供科学依据，具有较强的现实意义[1,2]。据人力资源和社会保障部最新统计资料显示，2014年高校毕业生的就业规模将达到727万，比2013年增加28万人，再创历史新高。运用科学方法及时预测出大学生的就业信心，对高校学生工作的开展尤为重要[3]。

严春红等借鉴经济领域中的消费信心指数，编制了浙江省高职院校的调查问卷，测度出大学生的就业信心指数，结果显示浙江省高职生的整体就业信心指数偏低[4]。杨光军等采用问卷调查方式研究了山东省德州市三所高校的就业信心指数，并用灰色模型法构建了基于时间序列的就业信心指数预测模型，可为高校制定长远计划提供参考依据[5]。然而在文[5]中，所构建的灰色模型仅对已有数据进行了拟合，缺少对模型的检验环节，模型的预测性能尚未得出。根据金菊良等的研究成果显示[6]，灰色模型法对具有趋势性的时间序列预测性能较好，但对周期性数据泛化能力较差，不如自回归法和神经网络法。

本文提出综合灰色模型法的趋势性预测性能和自回归法、神经网络法的周期性预测性能，利用遗传算法（GA）求解三种预测模型的权重，构建出基于GA的大学生就业信息指数组合预测模型（CombinationForecastingbasedonGAmethod，CF-GA）。

1 CF-GA模型构建

CF-GA模型主要思路是组合多个模型的预测性能，提高单模型的适用性。本文选用具有代表的自回归法（TAR）、神经网络法（BP）和灰色模型法（GM），分别运行预测模型，根据遗传算法（GA）计算出单模型的权重值，组合得到组合预测模型结果。因此，CF-GA模型的构建共包括如下6个步骤。

步骤1：数据预处理。

首先，需要对原始数据（X1,X2,…,Xn）进行无量纲化，消除量纲效应。

其次，根据待预测时间序列的数据分布特征，确定模型输入值、输出值的个数，构建样本对(Xn-k,…,Xn-1,Xn)，其中Xn为待预测年份的输出值，Xn-k,…,Xn-1，表示用前k年数据预测第n年的数据。模型构建过程，一般可应用数理统计中的自相关法，确定k值，考虑到大学生就业信心指数数据的小样本特点，实际使用中，k值可直接取2～4。

步骤2：自回归模型预测。

自回归模型(TAR)能有效地描述具有周期性、跳跃性、相依性等复杂现象的非线性动态系统，非常适合处理具有周期性的系统预测问题。其基本思想为：在观测时序{X(i)}的取值范围内引入L-1个门限值(r(j)，j=1，2，…，L-1)，将该范围分成L个区间，并根据延迟步数k将{X(i)}按{X(i-k)}值的大小分配到不同的门限区间内，再对不同区间内的X(i)采用不同的AR模型来描述，这些AR模型的总和完成了对时序{X(i)}整个非线性动态系统的描述。模型应用时需确定延迟步数k、门限个数L，及各个AR模型的系数，可用最小二乘法或遗传算法等优化算法求解。限于篇幅，本文不再展开，可参考文献[6]。

步骤3：神经网络模型预测。

BP神经网络是用BP算法训练的一种多层前馈型非线性映射网络，网络中各神经元接受前一级的输入，并输出到下一级，网络中没有反馈联接[7]。BP神经网络通常可以分为不同的层（级），第j层的输入仅与第j-1层的输出联接。BP算法是目前应用最为广泛且较成功的一种算法，在各行各业都有着广泛的应用，适合于预测样本中含有最大、最小值的插值式预测，对趋势性数据的外延性能较差。BP神经网络在应用时，需确定隐层节点个数，各层之间的连接系数可通过BP网络算法求解。

步骤4：灰色系统模型预测。

灰色系统预测模型来源于邓聚龙等提出的灰色系统，即用微分方程描述事物发展的连续过程，实现预测未来发展的目的，因此适合于预测具有趋势性特征的时间序列数据。杨光军等基于大学生就业信心指数数据，建立了GM预测模型，模型运行结果显示灰色系统模型可准确描述就业信心指数序列。与步骤2、3类似，对灰色系统模型预测更具体的内容可参考文献[5]。

步骤5：CF-GA组合预测模型。

假设，对同一就业信心指数有m个预测模型分别进行预测，记实际观测值为yd(t)，第i个预测模型的预测值为y(i,t)，第i个预测模型的权重为w(i)。其中：时刻t=1～n，n为样本容量；模型序号i=1～m；w (i)≥0，。则组合预测模型的预测值为

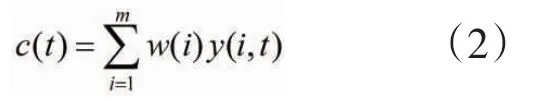
组合预测模型的预测误差绝对值为

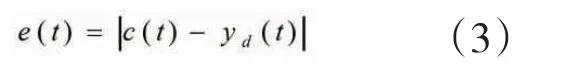
步骤6：遗传算法求解单模型权重

构建组合预测模型的关键是如何合理确定各单模型的权重值w(i)，实际上是一个非线性优化问题，遗传算法特别适合于解决此类问题[8]。金菊良等用遗传算法建立了预测海洋冰情的组合预测模型[9]，对提升单模型的预测效果十分明显，但经遗传算法优化后的单个模型权重值显著超过其它模型，如文[9]的权重值为{0.160,0.004,0.836}，预测性能依赖于第3个模型的预测结果，不利于综合利用其它模型信息，导致组合后的模型适用性较差。实际上，权重值系列为待定的概率密度函数簇。根据信息熵理论，在已有信息约束条件下，应从函数簇中选择熵值最大的密度函数，据此确定的密度函数更为客观[10]。

基于上述考虑，本文构建包含最小化预测误差绝对和、最大化权重值密度函数熵值的多目标函数，如式（4）所示，并用遗传算法求解，得出单模型的权重值。

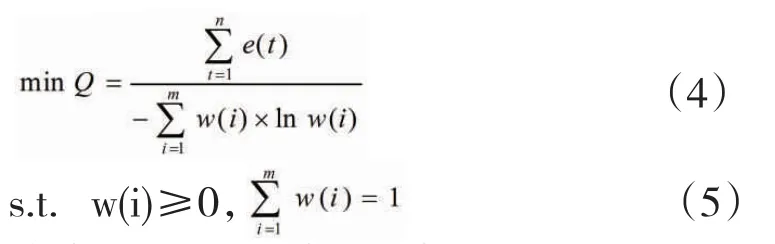
将求出的权重值w(i)代入式（2）中得到组合模型预测结果，与拟合期的TAR、BP、GM模型预测结果进行比较，分析组合三种单模型的CF-GA模型的拟合性能。然后，用没有参加拟合计算的数据样本，分别检验四种模型的预测性能，得出更为可靠的大学生就业信心指数预测结果，进而科学指导高校政策制定实践。

2 实例应用

2.1 数据来源

为便于比较，本文以文献[5]中采集的山东省德州市三所高校的就业信心指数数据为例，验证CF-GA模型的性能，预测大学生就业信心的变化趋势。文献[5]的就业信心指数位于0～200之间，数值越小表示越没信心，越大表示越有信心，数值100为“消极”与“积极”的临界值。图1显示2000～2012年大学生就业信心指数与经济景气指数的关系。

由图1可知，就业信息指数与经济景气指数的变化方向不一致，经济景气指数高的时候，就业信心指数相反处于低位，呈负相关关系，相关系数R=-0.254，且就业信息指数的波动性明显高于经济景气指数，说明仅用经济景气指数预测就业信心指数是不够的，可从就业信心指数的周期性出发加以预测。

图1 大学生就业信心指数与经济景气指数的关系

2.2 单模型预测

2.2.1 TAR模型预测

由于样本数据较少，模型的延迟步数k=2，TAR模型的门限个数L=1。根据最小二乘法计算结果，门限阈值为106.60，整理得到预测模型如下：

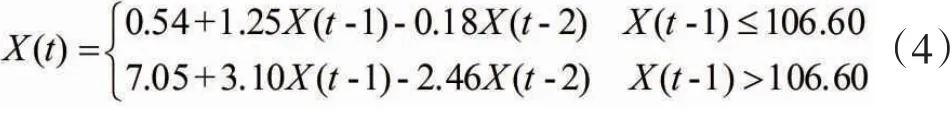
模型拟合期预测结果如表1中第Y_TAR列所示，拟合期误差绝对值和为92.75。分别用2009年、2010年数据预测2011年，2010年、2011年预测2012年就业信心指数进行检验。预测结果显示，2011年实测数据为122，预测结果为111；2012年实测数据为132，预测结果为131.4，说明所建立的TAR模型在拟合期和检验期都有很好的预测性能，可以作为组合预测模型的输入模型。

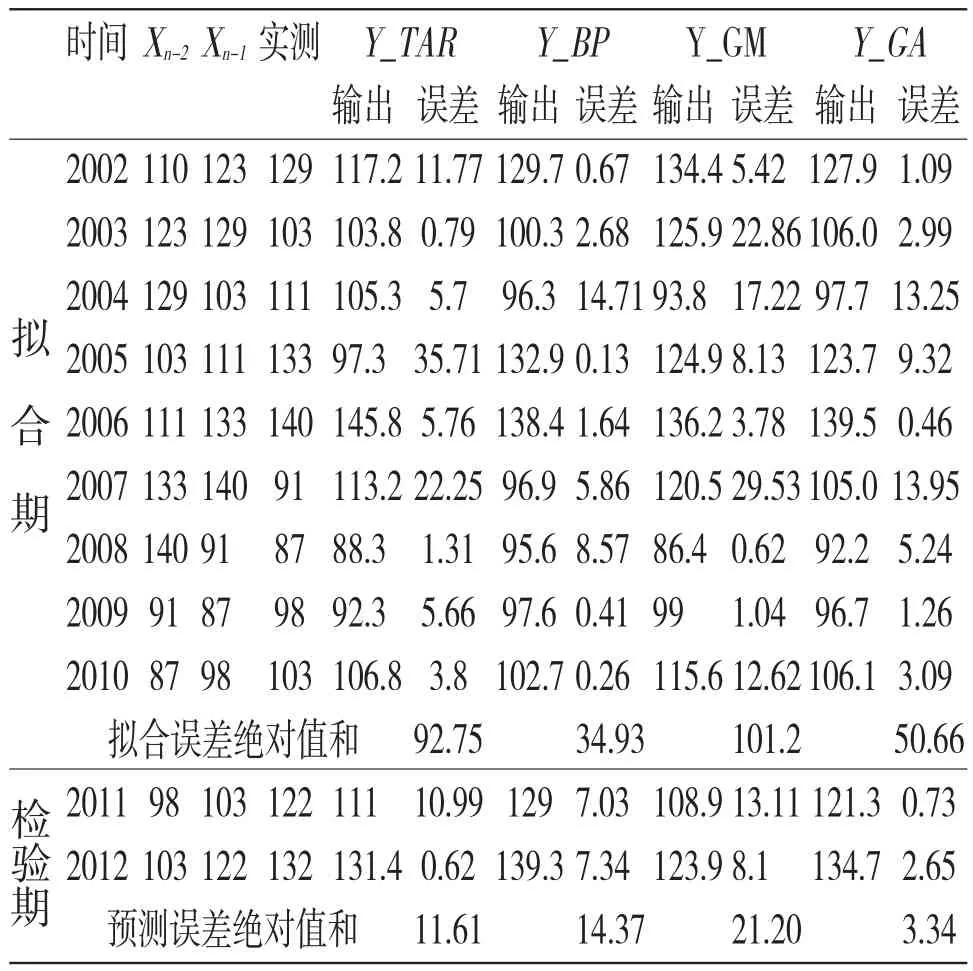
表1 CF-GA组合模型法预测结果误差分析

2.2.2 BP模型预测

BP模型网络结构中，输入层节点个数为2，隐层节点个数取3，输出层节点个数为1，将2000～2010年数据输入BP网络中，2011、2012年数据用作检验。预测结果如表1中第Y_BP所示，拟合期误差绝对值和为34.93。2011、2012年的检验结果显示，2011年实测数据为122，预测结果为129；2012年实测数据为132，预测结果为139.3，说明所建立的BP模型在拟合期和检验期也有较好的预测性能，可以作为组合预测模型的输入模型。相对于TAR模型，BP模型在拟合期的表现更加，但检验期的表现不如TAR模型，这与BP模型的拟合性能较强，泛化能力较弱有关。

2.2.3 灰色系统模型预测

表1中第Y_GM列出了文[5]中灰色系统模型的预测结果，GM模型在拟合期、检验期的误差绝对值和均大于相应的TAR、BP模型，说明GM模型在应对具有周期波动性的大学生就业信心指数预测中，表现不佳，与灰色系统模型适用于描述趋势性特征有关。

2.3 模型权重计算

为便于比较基于信息熵改进后的权重情况。分别用传统的不加熵误差绝对值最小化单目标函数和改进后的同时考虑误差绝对值最小化和熵值最大化的加熵多目标函数，进行对比，分别运用遗传算法求解单模型权重值，如表2所示。

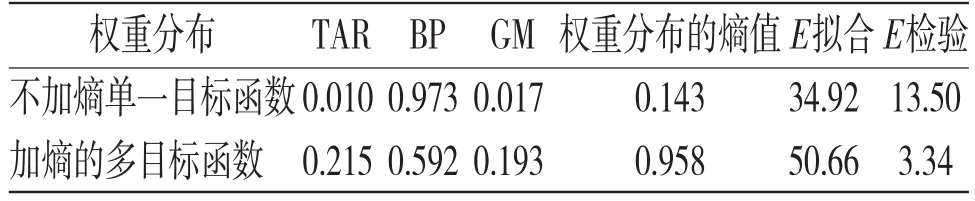
表2 基于遗传算法的单模型权重计算结果

表2显示，仅考虑误差绝对值最小化的单目标函数的权重求解结果，赋予了BP模型0.973的权重，而另外两个模型权重严重偏小。经计算权重分布的熵值为0.143，说明用该目标函数求解出的权重分布不确定性较大。据此权重分布计算拟合期的误差绝对值和为34.92，接近BP模型的34.93，而检验期误差绝对值和13.50超过了TAR模型的11.61，说明组合后的预测模型效果反而不如单模型的预测性能。

根据本文提出的引入信息熵理论，构造多目标函数求解出的权重分布较为合理，熵值0.958说明权重分布的不确定性较小，据此权重计算出的拟合期、检验期效果较好。

2.4 CF-GA组合预测

将三种模型（i=1,2,3）的拟合期（t=2002～2010）输出值y(i，t)和权重值w(i)式(2)中，得到组合预测模型的拟合期输出值，列入表1中第Y_GA列。CF-GA模型的拟合期误差绝对值和50.66劣于BP模型的34.93，但优于TAR和GM模型的92.75和101.2。说明组合三种模型后的CF-GA具有与BP模型接近的优秀拟合性能。

将三种模型的检验期（t=2011,2012）输出值和权重值代入式（2）中，可求出CF-GA模型的检验期预测值，其误差绝对值和仅为3.34，远小于GM模型的21.2和BP模型的14.37，也优于TAR模型的11.61，显示出较强的泛化预测能力。

组合模型与单模型预测结果比较见图2所示。进一步说明，综合多种单模型的预测信息后，CF-GA模型具有更加强大的适用性，尤其适合于应用于预测大学生信心指数，或者类似的时间序列预测问题。

图2 CF-GA组合模型与单个模型预测结果比较

2.5 预测结果讨论

从图2的CF-GA模型预测结果可知，虽然近年就业压力较大，但学生对就业的信心仍较高，且成逐年上升趋势。这与国家层面对大学生就业问题的重视，和制定的各种鼓励自主创业政策的实施，具有很大的关系。高校在面对当前的就业形势下，准确地获取大学生就业信心指数及其变化趋势，可及时调整高校学生工作重心，确保大学生对就业问题的信心。从图2可知，德州市的三所高校根据大学生就业信心指数，及时调整、制定了学生工作计划，将就业信心教育提升到大学生思想政治教育的层次上，同时多次举办各种职业规划和实践活动，解读国家和各级地方政府的就业政策，将大学生的就业信心指数稳定在了上升趋势中。

3 结论

（1）单个预测模型在大学生就业信心指数预测中，表现不同，BP模型具有较强的拟合能力，TAR模型具有较强的泛化能力，GM模型就业信心指数预测中表现一般。

（2）CF-GA组合预测模型，综合利用了单个预测模型的预测信息，极大地提升了模型的预测性能。CF-GA在拟合期的表现与BP模型接近，而在预测期则获得了远小于其它三种模型的预测误差，显示出强大的泛化预测能力。

（3）大学生就业信心指数的预测结果，可作为高校制定学生工作计划的依据。根据预测结果，及时调整工作方向，可进一步地稳定大学生的就业信心。

注释及参考文献：

[1]裴菁．上海市大学生就业区域流向的实证研究[J]．上海理工大学学报(社会科学版),2014(1):90-95．

[2]朱欣．我国大学生就业市场研究状况综述[J]．高校教育管理,2013,7(5):121-124．

[3]周红霞．大学生就业信心状况调查与对策分析[J]．东北师大学报(哲学社会科学版),2011(3):214-217．

[4]严春红．大学生就业信心指数的设计与分析[D]．金华:浙江师范大学,2007．

[5]杨光军．灰色神经网络在大学生就业信心指数预测中的应用[J]．计算机系统应用,2013,22(8):190-193．

[6]金菊良,丁晶,魏一鸣．基于遗传算法的门限自回归模型在浅层地下水位预测中的应用[J]．水利学报,1999(6)：51-55．

[7]张铃,张钹．神经网络中BP算法的分析[J]．模式识别与人工智能,1994,7(3):191-195．

[8]汪应洛．系统工程[M]．北京:机械工业出版社，2008:120-125．

[9]金菊良,魏一鸣,丁晶．用基于加速遗传算法的组合预测模型预测海洋冰情[J]．系统管理学报,2003,12(4):367-370．

[10]张明,金菊良,张礼兵．信息论方法在水资源系统工程中的应用[J]．中国人口·资源与环境,2007,17(2):79-83．

Combination Forecasting of the Employment Confidence Index of College Student by GeneticAlgorithm

ZHOU Run-juan,CAI Jin-ping,HU Chang-xin
(College of Electrical Engineering,Anhui Polytechnic University,Wuhu,Anhui 241000)

Employment confidence index of college student(ECI)can be used as a reference to assist the university administrators to formulate work plans and cope with the current employment situation.So,the most accurate forecasting results are needed,which is directly related to the effect of policy formulation and implementation.In order to solve this problem,the advantages and disadvantages of the model of threshold auto-regression(TAR),back propagation(BP)and gray model were analyzed.According to analysis result,we propose a combined forecast model based on the genetic algorithm(CF-GA),in which GA is used to determinate the weight of each single model.The forecast results show that the performance of CF-GA has a good behavior to other three models,which can be used as an important reference for the university development of relevant policies.

college student employment;confidence index;combination forecasting;genetic algorithm;entropy

G647.38

A

1673-1891（2015）03-0077-04

2015-05-11

教育部人文社会科学研究专项任务项目（项目编号：12JDSZ3041）;安徽高校省级科学研究项目（项目编号：2011sk637）;安徽工程大学青年科研基金项目（项目编号：2013YQ38）。

周润娟(1984-),女,安徽太湖人,硕士,助教,研究方向:环境污染综合治理。