Fault Detection Based on Incremental Locally Linear Embedding for Satellite TX-I

(程月华)， (胡国飞)， (陆宁云)，

1.College of Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, P.R. China 2.College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, P.R. China 3.National Laboratory of Space Intelligent Control, Beijing Control Engineering Institute, Beijing 100000, P.R. China (Received 4 November 2014; revised 24 March 2015; accepted 25 April 2015)

Fault Detection Based on Incremental Locally Linear Embedding for Satellite TX-I

ChengYuehua(程月华)1*，HuGuofei(胡国飞)2，LuNingyun(陆宁云)2，

JiangBin(姜斌)2，XingYan(邢琰)3

1.College of Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, P.R. China 2.College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, P.R. China 3.National Laboratory of Space Intelligent Control, Beijing Control Engineering Institute, Beijing 100000, P.R. China (Received 4 November 2014; revised 24 March 2015; accepted 25 April 2015)

A fault detection method based on incremental locally linear embedding (LLE) is presented to improve fault detecting accuracy for satellites with telemetry data. Since conventional LLE algorithm cannot handle incremental learning, an incremental LLE method is proposed to acquire low-dimensional feature embedded in high-dimensional space. Then, telemetry data of Satellite TX-I are analyzed. Therefore, fault detection are performed by analyzing feature information extracted from the telemetry data with the statistical indexesT2and squared prediction error(SPE) and SPE. Simulation results verify the fault detection scheme.

incremental locally linear embedding (LLE)； telemetry data； fault detection； dimensionality reduction； statistical indexes

0 Introduction

Satellite engineering has been increasingly critical in spacecraft research[1]. Satellites in orbit transmit telemetry data to identify satellite running status and implement tasks[2]. Significant improvements in space technology inevitably lead to more complex behavior of satellites, which in turn brings about higher demand for reliability. Meanwhile, large-volume telemetry data make data analysis difficult. Conventional data-driven fault diagnosis encounters significant challenges when applied to satellites.

Since fault information is contained in satellite telemetry data, quite a number of fault diagnosis methods have been proposed based on the features extracted from the data. Yu et al. developed a fault detection and diagnosis (FDD) scheme by combining principal component analysis (PCA) with support vector machines (SVRs)[3]. However, feature extraction based on PCA do not work well with nonlinear data. Fujimaki et al. proposed a novel ″knowledge-free″ anomaly detection method for spacecrafts based on kernel feature space (KFS) and directional distribution, which employed normal historical telemetry data to construct a system behavior model and then monitored current system running by comparing incoming data with the model[4]. However, the selection of the consistency of appropriate kernels for heterogeneous multidimensional data is inconvenient for its applications. Yang et al. presented several data-mining methods based on data-driven FDD for satellite telemetry data, which showed great potential[5]. Recently, several novel feature extraction methods based on manifold learning have been reported for handling nonlinear high-dimensional data. A new approach was adapted for intelligent fault diagnosis based on locally linear embedding (LLE)[6], a kind of manifold. An extended LLE algorithm was also introduced in Ref.[7]. Manifold learning has been demonstrated in various applications such as face recognition[6]and machinery fault diagnosis[8].

Most of these algorithms are operated in a batch mode,i.e., all data are available for training. Nevertheless, they fail to provide a model or formula to extract features for sequentially incoming data. When new data arrive, one needs to execute the entire algorithm again with original data augmented by new data. This restricts these algorithms′ applications, especially in a changing and dynamic environment.

Information can be ascertained with new incoming incremental data. Various incremental manifold learning methods have been proposed[9-11]. We introduce Satellite TX-I, as the research object, with telemetry data. It is unrealistic to expect to directly grasp the features of these data because of complex working conditions. To extract features of parameters in telemetry data, an incremental LLE algorithm is employed herein. Then, the anomalies hidden in the data can be detected by using statistical indexesT2and squared prediction error (SPE) and SPE acting on the extracted features.

1 Preliminary Overview

How to extract useful information from massive data in this age is a big challenge for data analysis. In the past decades, manifold learning, a new type of feature extraction method, was developed. Compared with other linear methods, manifold learning provides an effective way to handle nonlinear data. The LLE algorithm is an unsupervised manifold learning method that extract features based on geometric intuition.

1.1 Conventional LLE

Step3Computethelow-dimensionalembededYofXwithoutchangingthereconstructionweightsobtainedinStep2.

In Step 2, the optimal weights can be obtained by solving the constrained least-squares problem as

(1)

In step 3, the dimensionality reduction is utilized by retaining the same reconstruction weights between the points and the corresponding neighbors. Each high-dimensional input xiismappedintoalow-dimensionaloutputyirepresenting global internal coordinates in the manifold, which can be accomplished by minimizing the embedding cost function

(2)

However, the LLE algorithm performs dimensionality reduction in a batch mode, which means that the LLE fails to provide an explicit way of mapping the high-dimensional space into the embedded feature space. When new data points arrive, one has to rerun the LLE algorithm to achieve the low-dimensional features with an augmented data set. Considerating some special cases, like large data sets with high dimensionality in a dynamic environment, the LLE algorithm seems to be less attractive because it fails to accommodate new data. Thus, the incremental LLE (I-LLE) algorithm gradually becomes interesting and appealing.

1.2 Incremental LLE

Many attempts have tried to tackle the problems mentioned above, including local linear regression (LLR)[12]and local linear projection (LLP)[13]. Assuming that the embedded manifold is locally linear, LLR and LLP are conducted to reveal implicit projection between high-dimensional space and embedded feature space. The implementation of LLP algorithm is presented in Table 1.

Table 1 Implementation of LLP

In Step 2, the linear least-squares regression problem can be presented as

(3)

With the aid of LLP, one can directly calculate the low-dimensional representation without repeatedly carrying out the complex LLE algorithm. Eq.(3) shows that different mapping matrices are developed for each new sample, which can ensure the accuracy of the calculated embedding to a certain extent. Furthermore, a fixed mapping matrix can be used because the new samples are geometrically similar. Then, the LLP algorithm can be seen as LLR, which only uses the whole structure of the data set without findingknearest neighbors for a new incoming sample. Namely, the solid mapping matrixAis calculated with the original training setXand the associated low-dimensional coordinatesYandY=AX.

However, LLP is to find low-dimensional representations of the new data without a feedback loop. By extending the neighbors directly, the dimensionality reduction algorithm cannot guarantee optimal results. In other words, not only the low-dimensional embedding of the new incoming data but also the effects of these data on the original data set should be taken into account. In this paper, novel I-LLE is presented to map new samples into the low-dimensional feature space with a feedback loop.

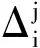
Step 1 Update the weight matrixWwith the help of the Euclidean distance criteria;

Step 2 Recompute the cost functionMcorresponding to the change ofW.

Given a new incoming sample xnew,finditsknearestneighborsandcomputethecorrespondingweightvector,denotedasWnew. Step 1 is described in Table 2.

Table 2 Weight matrix update

Only the changed neighbors have been considered when updating the weight matrix, which greatly improves the efficiency of the I-LLE algorithm. From a mathematics perspective, procedure (1) focuses on xi,whoseneighborshavebeenupdated.Finally,anew(N+1)×(N+1)weightmatrixW′is obtained from updating the weight matrixWaugmented by the weight vectorWnew.

Determining How to facilitate the new weight matrix to find low-dimensional representation naturally promotes research on cost matrixM′. As mentioned in Section 1.1, the calculation of the cost function can be ″translated″ as

(4)

Since only a local part of the weight matrix is updated, one can calculate the cost function in terms of the mutative points. Compared to the conventional LLE, I-LLE greatly improves the efficiency of calculating a new embedding when an existing data set is being slightly modified. Furthermore, it considers not only the explicit mapping from samples into embedded space but also the effects of the new samples on the original data set.

I-LLE provides a way to acquire low-dimensional embedding of the samples without entirely rerunning the LLE algorithm.

2 Feature Extraction for Telemetry Data

Since Satellite TX-I transmit large amounts of telemetry data to ground stations every day， it is an realistic to grasp the embedded features through visualization. However， the I-LLE algorithm can exposed hidden features of the data only if specific cases are taken into account.

2.1 Basic features of telemetry

2.1.1 Observable area

A satellite travels in its orbit and transmits data to ground stations in a specified area. Telemetry data of Satellite TX-I are from an arc area in orbit, e.i.， the so-called observable area. The observable area is so small that the observation time is very limited. Therefore， only finite telemetry data are sent to ground stations. Furthermore, the cycle period of the observable area can be known only if the satellite is operated in a normal model.

2.1.2 Rising orbit and descending orbit

The wholel orbit around the Earth can be divided into two parts: Rising orbit and descending orbit, which correspond to the local nighttime and daytime, respectively. In terms of latitude, a satellite in rising orbit moves from south to north; while the opposite moving tendency means the satellite in descending orbit. Moreover, these two tendencies have different effects on system parameters. Even the same parameters may present different features in different orbit regions. In this study, parameters related to the satellite attitude control system are taken into account to demonstrate the effects of the orbit tendencies.

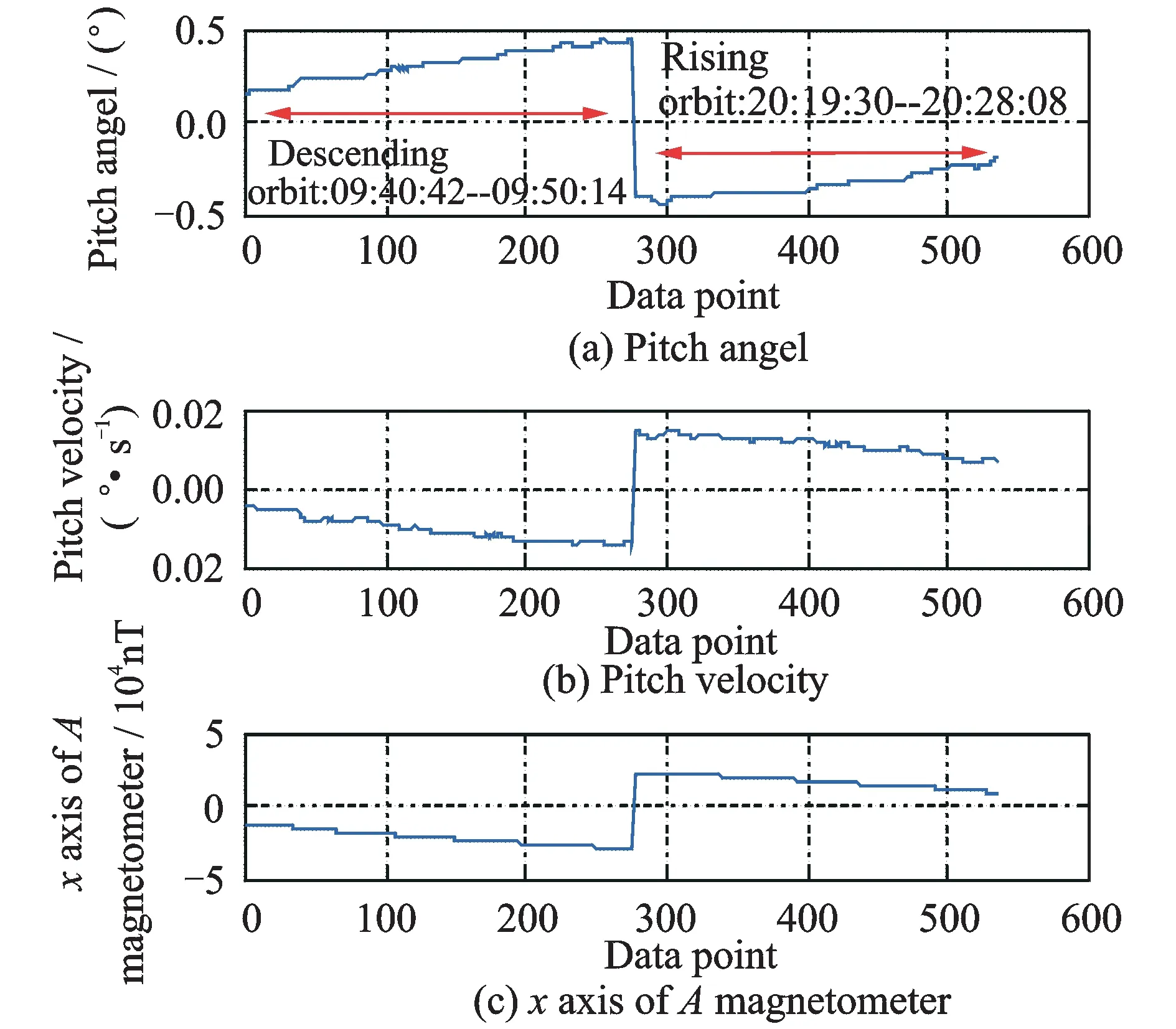
Fig.1 Telemetry data of different parameters on 1 January 2012

For Satellite TX-I, the telemetry data of three parameters， pitch angle, pitch velocity, andxaxis of magnetometerA， are presented in Fig.1. Fig.1 implies the effects of the couple orbits on the parameters. Furthermore, the single orbit (rising or descending) remains for a short period for each parameter as the small observable area mentioned in subsection 2.1.1. Meanwhile,the curves in Fig.1 are unsmooth because of the noise in telemetry data. For Satellite TX-I, the realtime telemetry data points are transmitted to a ground station every 2 s. In Fig.1, the descending orbit of the pitch angle covers almost 286 points. In other words, the descending orbit remains for almost 10 min, which can be calculated from the detailed time shown in Fig.1.

The features of the couple orbits perfectly demonstrate that parameters hold various features in different orbits, which should be considered for future feature extraction.

2.1.3 Illumination

As they revolve around the Earth, satellites are not always exposed to sunlight, which can affect the operation mode. Specifically, the energy working condition on the shady side significantly differs from that in the illumination region. As an example, the charging current and the discharge current of TX-I on 1 January 2012 are shown in Fig.2. Charging current runs beyond zero under the illumination condition, while the discharge current stays around zero, which illustrates that illumination ′perturbs′ the working condition of the energy system in satellites. To comprehend the energy system of Satellite TX-I, the solar cell current on the same day is also presented in Fig.2.

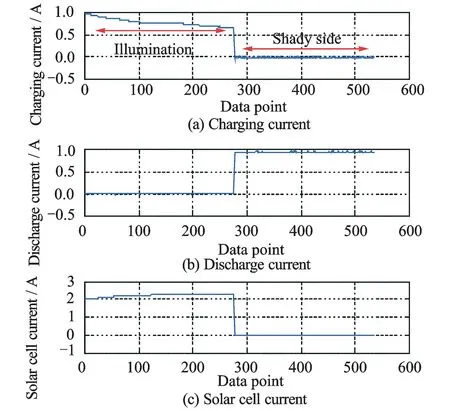
Fig.2 Telemetry data of current on 1 January 2012

Therefore， features of the parameters are greatly affected by working conditions and environment. It is possible to capture the feature of a single parameter from corresponding telemetry data but the fact that hundreds of satellite parameters remain to be analyzed makes this single-parameter-based analysis impractical. Furthermore, several parameters are needed to study a subsystem， including a satellite attitude control system, which greatly increases the difficulty. Thus, the I-LLE algorithm is employed to perform feature extraction.

2.2 Application of I-LLE to feature extraction

Feature extraction mainly in clude two aspects: (1) Dimensionality reduction, which provides the low-dimensional presentation for the high-dimensional space; and (2) the preservation of the main features. In other words, the main features of the data are retained, while the redundant information should be ignored or discarded. Therefore, feature extraction plays an important role in data analysis. Furthermore, feature extraction should be performed by considering that the real-time telemetry data are affected by working conditions.

In this section, the telemetry data of some parameters are used as ″guinea pigs″ to validate the I-LLE algorithm. To avoid losing generality, five parameters related to the satellite attitude from 1—5 January 2012, are employed. Additionally, only one kind of the orbits (the rising or the descending) are considered due to the feature differences between the two orbits. However, the I-LLE algorithm can not be operated until it complete some preliminary treatments on the telemetry data. First of all, it must remove the outliers falling short of the overall trend. Then, filtering method is highly recommended as it can consequently improves the feature extraction efficiency. In addition, normalization for different units of different parameters is in great demand.

The pretreated 276 data points on 1 January 2012 are used as the training data, while the data points from 2—5 January 2012, are used as the testing data, which are shown in Fig.3(a).

The ILLE-based feature extraction should set two parameters in advance: Reduced dimensionality (intrinsic dimensionality)dand the number of neighborsk. In addition, the effects of these two parameters should not be ignored. Takedas an example. Ifdis set too large, the mapping of I-LLE will contain a great deal of redundant information and enhance the noise; on the contrary, a smalldmay lead to embedded data overlapping. The selection of these parameters is beyond the scope of this paper. Several methods of determining the parameters have been provided[6，14，15]. We setd=3 andk=12. To directly compare the I-LLE algorithm with the conventional LLE algorithm, the dimensionality reduction results for the telemetry data from 2—5 January 2012 are shown in Fig.3.

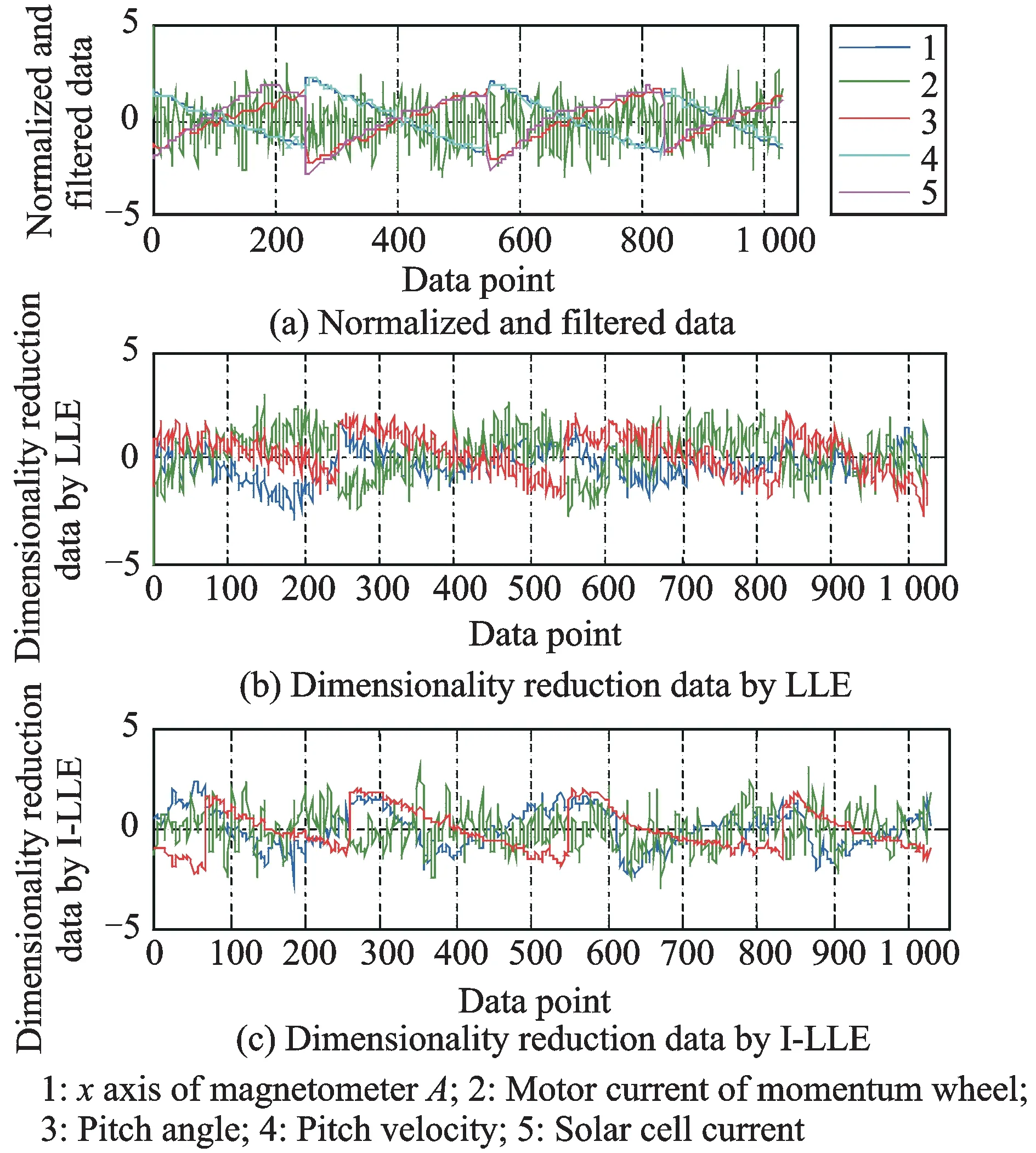
Fig.3 Pretreated data for 2—5 January 2012, and dimensionality reduction results

Fig.3 shows that the I-LLE algorithm can also reduce dimensionality like the conventional one. As discussed in Section 2, I-LLE performs the feature extraction with a feedback loop, which greatly improves the accuracy of the extraction. The accuracy of the conventional LLE algorithm can be somewhat improved by changing its parameters, likekwithout a feedback loop while neglecting performance efficiency. The difference is that the I-LLE algorithm only takes the changed part into account without running the entire algorithm, which improves execution efficiency. And using feedback loop directly affects the accuracy of feature extraction. Meanwhile, the I-LLE algorithm has the potential to map the high-dimensional fault samples into embedded low-dimensional space with obtaining the fault information, which finally can be used as a tool to perform fault detection.

3 Fault Detection

Unlike conventional model-based fault detection methods, the I-LLE algorithm is good at solving data-based problems. In many cases, the reality model of the samples was located in a low-dimensional manifold embedded in the high-dimensional sample space[16，17]. From a geometry perspective, the data belonging to the same fault class lie in or near a manifold embedded in the high-dimensional space[18]. In other words, with the help of the feature extraction of I-LLE, the fault information can finally be enveloped in the embedded space. Thus, a new fault detection based on an I-LLE algorithm is presented. By capturing the embedded manifold feature, the algorithm maps the high-dimensional space into a low-dimensional embedded space to detect faults. To visualize the fault information, the statistical indexesT2and SPE and SPE are employed herein.

3.1 Fault detection scheme

As mentioned previously, fault detection is performed in the embedded space by using the statistical indexesT2and SPE and SPE. The main problem is how to use these indexes to monitor the embedded space. At the macroscopic level, the I-LLE algorithm is a kind of modeling problem. Thanks to the new incoming data, I-LLE continually updates its original database (seen as the model), starting with the training data. Meanwhile, the statistical indexesT2and SPE and SPE should be introduced to sense the variation of the new incoming samples and use the normal operating condition model.

SPE is adopted to measure the noisy part of the process information and the variability deviating from the normal operating condition model, which is also called the residual space. The calculation of SPE for a new incoming sample is presented as

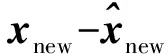
(5)

(6)

whereΛis the sample covariance matrix ofYin the normal operating condition that is

(7)

The statistical indexesT2and SPE and SPE not only ensure the use of the normal model for I-LLE but also promote the fault detection scheme that is presented as follows:

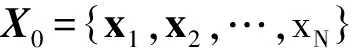
Step 2 Perform the conventional LLE algorithm onX0to obtain the embedded low-dimensional coordinatesY0;

Step 3 Approximate the mapping matrixA0that satisfiesY0=A0X0by using the LLR method;

Step 4 Obtain the new incoming data; filtering and normalization should be conducted to obtainXnew;

Step 5 Conduct dimensionality reduction with the help of the mapping matrix ,A0i.e.,Ynew=A0Xnew;

Step 6 Calculate the statistical indexesT2and SPE and SPE for the new embedding and present the fault detection result;

Step 7 Update the mapping matrixA0by performing the I-LLE algorithm with the normal new dataXnew;

Step 8 Repeat Steps 4—7.

It can be seen that the I-LLE algorithm is performed on the new incoming data that are taken to update the I-LLE model. The database is refreshed, and then the embedding space is updated. Undoubtedly, the mapping matrix will be revised, which can ensure the accuracy of the dimensionality reduction. Meanwhile, the LLR method is used herein because of the geometrical similarity of the telemetry data between different dates.

3.2 Case Study

In this study, the telemetry data of Satellite TX-I on 1 January 2012 are employed as the training set, which triggers the execution of the I-LLE algorithm on the telemetry data from 2—5 January 2012. Moreover, only the data of the descending orbit are adopted. The intrinsic dimensionalityd=3 and the number of the neighborsk=12. To verify the performance of the fault detection scheme based on the I-LLE algorithm, numerical simulations of different fault types are presented in the following sections.

3.2.1 Case 1: Constant fault for pitch velocity

The constant bias occurs from 120 to 170 points of pitch velocity. To illustrate the I-LLE algorithm, the statistical detection results are shown in Fig.4. Furthermore, Fig.5 presents the detection results based on the conventional LLE algorithm.

Fig.4 Statistic detection results for constant fault based on I-LLE algorithm

Fig.4 shows that bothT2and SPE and SPE change over the threshold when fault information is introduced. In addition, the false alarm rate (FAR) and the missing alarm rate (MAR) for these statistical indexes are given in Tables 3,4. The results based on LLE, by contrast, do not show a promising perspective. The corresponding FAR and MAR are also given in Tables 3,4. Although both algorithms can correctly detect the fault information, the results based on LLE sometimes provide misleading data. Owing to the effect of the feedback loop, the thresholds of the statistical indexes in I-LLE are metabolic. In the conventional LLE algorithm, there is no feedback loop, which means that the database will not be refreshed. Additionally, the LLR method, which is used to find the mapping matrix, determines the static thresholds for the statistical indexes because the training data are set.

Table 4 FAR and MAR of T2 statistic with constant fault

3.2.2 Case 2: Time-varying fault for pitch velocity

Time-varying fault occurs from 120 to 170 points. The fault detection scheme based on the I-LLE algorithm is applied to obtain the statistical results presented in Fig.6. Fault detection based on the conventional LLE algorithm is shown in Fig.7. Intuitively, FAR and MAR of the statistical indexes for the algorithms are first provided in Tables 5,6.

Table 5 FAR and MAR of SPE statistic with time-varying fault

Table 6 FAR and MAR of T2 statistic with time-varying fault

Compared with Case 1, the time-varying fault detection does not perform as well. However, the statistical indexes based on the I-LLE algorithm show great adaptability, while those based on the conventional LLE algorithm remain in a conservation position, which can also be seen in Figs.6,7.

Fig.6 Statistic detection results for time-varying fault based on I-LLE algorithm

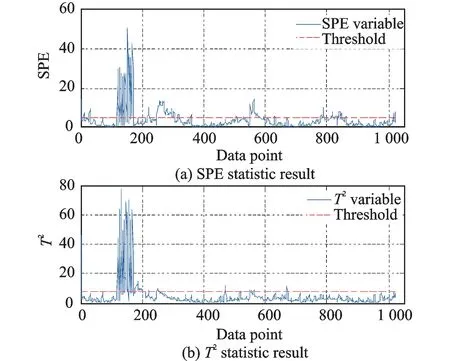
Fig.7 Statistic detection results for time-varying fault based on LLE algorithm

Fig.6 shows that the indexes jump over their associated threshold when the fault occurs and return to normal when the fault disappears. However, the performance of the fault detection based on LLE does not meet expectations, which can determined from Tables 5,6. Overall, both I-LLE and LLE can complete fault detection tasks, but I-LLE greatly improves detection accuracy.

4 Conclusions

A fault detection approach based on I-LLE is presented. After a brief introduction of the telemetry data of Satellite TX-I, I-LLE is employed to extract data features and capture the low-dimensional embedding, which leads to the development of fault detection scheme. Finally, fault detection for the TX-I telemetry data based on the I-LLE algorithm is carried out on the embedded low-dimensional space. To illustrate the potential of the proposed scheme, simulations are provided.

However, the parameters of I-LLE, like intrinsic dimensionality, should be set in advance, which will influence the fault detection performance. Therefore, the detailed selection of these parameters is worthy of further study.

Acknowledgement

This work was supported by the Fundamental Research Funds for the Central Universities(No.2016083).

[1] Hou Q, Cheng Y, Lu N, et al. Study on FDD and FTC of satellite attitude control system based on the effectiveness factor[C]∥Systems and Control in Aerospace and Astronautics. China:IEEE, 2008:1-6.

[2] Crowley N L, Apodaca V. Analysis of satellite telemetry data[C]∥Aerospace Conference, 1997. USA:IEEE, 1997: 57-67.

[3] Gao Y，Yang T，Xing N，et al. Fault detection and diagnosis for spacecraft using principal component analysis and support vector machines [C]∥2012 7th IEEE Conference on Industrial Electronics and Applications. Singapore:IEEE,2012:1984-1988.

[4] Fujimaki R，Yairi T，Machida K .An approach to spacecraft anomaly detection problem using Kernel Feature Space [C]∥ IEEE Aerospace Conference.USA:IEEE, 1997: 57-67.

[5] Yang T, Chen B, Gao Y, et al. Data mining-based fault detection and prediction methods for in-orbit satellite[C]∥Measurement, Information and Control (ICMIC), 2013 International Conference on. Egypt:IEEE, 2013:805-808.

[6] Jiang Q, Jia M, Lv J. New approach of intelligent fault diagnosis based on LLE algorithm[C]∥ Control and Decision Conference, 2008. China:IEEE, 2008:522-526.

[7] Miao A, Song Z, Zhiqiang G E, et al. Nonlinear fault detection based on locally linear embedding[J]. Journal of Control Theory & Applications, 2013, 11(4):615-622.

[8] Zhang W, Yang X. Fault detection method based on extended locally linear embedding[C]∥ Industrial Electronics and Applications, 2006 1st IEEE Conference on. Singapore: IEEE, 2006:1-4.

[9] Kouropteva O, Okun O, Pietikäinen M. Incremental locally linear embedding algorithm[M]∥ Image Analysis. Germany: Springer Berlin Heidelberg, 2005:521-530.

[10]Law M H C, Jain A K. Incremental nonlinear dimensionality reduction by manifold learning[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2006, 28(3):377-391.

[11]Shi Lukui, Yang Qingxin, Liu Enhai, et al. An incremental manifold learning algorithm based on the small world model[C]∥ Final Program and Book of Abstracts of the 2010 International Conference on Life System Modeling and Simulation & 2010 International Conference on Intelligent Computing for Sustainable Energy and Environment.China:LNCS, 2010:324-332.

[12]Ma Y, Wang M, Shi H. Fault detection for chemical process based on locally linear embedding[J]. Ciesc Journal, 2012,63(7):2121-2127.

[13]Zhang J，Li S Z，Wang J. Nearest manifold approach for face recognition[C]∥ 2013 10th IEEE International Conference and Workshops on Automatic Face and Gesture Recognition. Korea:[s.n.], 2004: 223-228.

[14]Li B, Zhang Y. Supervised locally linear embedding projection (SLLEP) for machinery fault diagnosis[J]. Mechanical Systems & Signal Processing, 2011, 25(8):3125-3134.

[15]Saul L K, Roweis S T. Think globally, fit locally: Unsupervised learning of nonlinear Manifolds[J]. Journal of Machine Learning Research, 2003, 4(2):119-155.

[16]Seung H S，Lee D D, The manifold ways of perception [J]. Science, 2000, 290(5500):2268-2269.

[17]Roweis S T, Saul L K. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 2000, 290(5):2323-2326.

[18]Jiang Q, Jia M, Hu J, et al. Machinery fault diagnosis using supervised manifold learning[J]. Mechanical Systems & Signal Processing, 2009, 23(7):2301-2311.

[19]Cai L, Tian X, Zhang Y. Dynamic process monitoring based on orthogonal locality preserving projections and exponentially weighted moving average[C]∥The 25th Chinese Control and Decision Conference. China: Northeastern University Press ,2013:4337-4342.

[20]Zhang Ni, Tian Xuemin. Nonlinear dynamic fault detection method based on isometric mapping[J]. Journal of Shanghai Jiaotong University, 2011, 45(8):1202-1206.(in Chinese)

(Executive Editor： Zhang Bei)

V467 Document code:A Article ID:1005-1120(2015)06-0600-10

*Corresponding author: Cheng Yuehua, Associate Professor, E-mail: chengyuehua@nuaa.edu.cn.

How to cite this article: Cheng Yuehua, Wang Tao， Lu Ningyun, et al. Fault detection based on incremental locally linear embedding for satellite TX-I[J]. Trans. Nanjing U. Aero. Astro., 2015,32(6):600-609. http://dx.doi.org/10.16356/j.1005-1120.2015.06.600