某矿井下开采地表沉降范围及发展趋势
刘诗杰 李 铁 马海涛 刘三平
(1.北京科技大学土木与环境工程学院,北京 100083;2.金属矿山高效开采与安全教育部重点实验室,北京 100083;3.中国安全生产科学研究院,北京 100012;4.矿山采空区灾害防治国家安全生产监督管理总局安全生产重点实验室,北京 100012)
某矿井下开采地表沉降范围及发展趋势
刘诗杰1,2,3李铁1,2马海涛3,4刘三平1,3
(1.北京科技大学土木与环境工程学院,北京 100083;2.金属矿山高效开采与安全教育部重点实验室,北京 100083;3.中国安全生产科学研究院,北京 100012;4.矿山采空区灾害防治国家安全生产监督管理总局安全生产重点实验室,北京 100012)
通过概率积分法与数值模拟相结合的方式,对山东某铁矿井下开采对地表周边民居建筑的影响进行了研究。分析表明,矿区周边居民住宅位于开采沉降范围边界处,地表变形的倾斜、曲率、水平移动分别为0.08 mm/m、0.009×10-3m、0.4 mm/m,符合相关规范要求;数值模拟地表沉降范围较概率积分法计算结果大,同一截面处对比显示,数值模拟中地表沉降宽度达407.6 m,大于概率积分法的366.7 m。矿区沉降监测数据的拟合分析表明,该区域近年来沉降变化斜率小于0.03,地表稳定,没有新的沉降变形趋势。因此,可以认为周边居民小区住宅不会因井下作业受到影响。概率积分法中反映覆岩岩性影响的参数选取可能引起误差,导致依概率积分法计算结果与数值模拟存在差别,在实际运用中应当通过多种方法协同论证,确保结论正确,实现井下生产与居民生活的和谐稳定。
概率积分法地表沉降数值模拟FLAC
矿山井下开采作业引起的地表沉降变形发展缓慢,时间效应长,影响范围广,且影响沉降分布因素复杂,个别极端案例中,地表因地下空区冒落产生大面积塌陷灾变,造成巨大人员、财产损失。因此,针对空区变形引起的地表沉降量及范围的研究具有极高的经济、社会效益[1-2]。
为了减少开采引起的地表沉降对矿区居民、建筑的影响,我国政府出台了相关规范[3],各矿山也积极改进采矿方法,使用充填体处理空区,以取代崩落法作业,取得了良好效果。过往也有许多学者对沉降相关理论进行了研究,提出了如概率积分法,典型曲线法,剖面函数法以及灰色模型理论等分析方法。概率积分法[4-5]为适用于非连续介质模型的影响函数法,综合考虑了岩层性质,空区深度,矿房高度,是否揭露地表等多种因素,相关研究较为充分,因而被广泛应用于各大矿山地表沉降范围及沉降量分析中。概率积分法可以求得一定面积、深度下的空区引起的地表沉降范围与沉降分布特征参数,通过将特征参数与相关规范对比,即可判断该区域是否安全稳定。
1 工程概况
山东某铁矿采区面积1.484 km2,年产量45 万t/m,开采矿体埋深+250~-400 m,位于闪长岩与大理岩接触带内,顶板为大理岩,上覆岩层以灰岩、页岩为主,地表覆盖有一定厚度的第四纪地表土。矿体形态不规则,呈NE—WS分布,主矿体走向长约1 300 m,倾角40°~80°,属急倾斜矿体。
矿区东北侧有一在建商业居民小区,该小区为钢筋混凝土结构,距离矿区较近;矿区南部及其他周边位置也分布有少量普通居民楼房,易受采动影响。该矿平面概况如图1所示。

图1 矿区概况
该矿从建矿之初一直以崩落法对0 m以上矿段进行开采,在矿区内形成了范围巨大的沉陷区域及塌陷坑,对矿区地貌造成了巨大破坏,在矿区北部形成一个沉降量较大的沉降中心。2006年后,采矿方法改为下向进路尾砂胶结充填法,并对历史遗留空区进行了回填处理。经检验,空区充填率达90%以上,充填效果良好。
根据经验,充填率达到90%以上的空区顶板沉降变形量极小,不会对地表建筑造成影响[6],但也曾有过因充填体质量或局部充填率不达标造成地面不均匀沉降的案例。因此,对矿区地表沉降的研究一方面要计算历史遗留空区变形引起的沉降,圈定沉降范围,确定相关参数,另一方面应基于监测数据对充填处理空区后的地表沉降发展趋势进行预测研究,确保地表居民建筑安全。
2 沉降范围计算
2.1概率积分法
作为开采沉陷的主体,岩体的接触形式可用连续介质模型与非连续介质模型描述。概率积分法基于非连续介质模型,认为岩体介质由极小单元组成,单元之间无应力联系,允许相对运用。在研究各单元移动规律时,该方法假设岩移为完全随机形式,服从正太分布[7-8],其理论模型如图2所示。对于一定面积与范围的地下空区,其上部不同位置处的岩层向临空方向移动概率依竖向、水平距离的变化呈正态分布,因此形成的下沉盆地形式与正太分布函数曲线一致。

图2 概率积分法理论模型
空区顶板重心的下沉量wmax并非等于空区高度,而是与矿体倾角α,采厚m,下沉系数q相关,满足
wmax=qmcosα.
(1)
基于该最大下沉量wmax,结合正态分布函数可求得沿倾斜剖面的下沉量w(y)、倾斜度iy、曲率Ky和水平应变εy,即
(2)
式中,y为距开采中心距离,m;b为水平移动系数;θ为开采影响传播角,与矿体开采角有关,即
α≤45ο时,θ=90ο-0.68α,
α≥45ο时,θ=28.8ο+0.68α;
r为影响半径,r=H/tanβ,β为影响范围边界与开采边界的直线与水平所成的夹角,
tanβ=(1-0.003 8α)(D+0.003 2H);
(3)
D为岩性影响系数,岩性坚硬取0.7~1.25,中硬取1.2~2.0,软弱取2.0~2.8[9];H为矿体埋深,m。
2.2沉降范围计算
该矿矿体走向较长,将矿体按走向划分并编号0~43切线,对各切线矿体剖面分别计算。限于篇幅,在此仅列出3线剖面图及相关计算。对剖面矿体集中段分别进行编号计算,如图3所示。
衬垫采用的COOLMAX材料,需要贴近人肌肤的外表面采用超疏水自清洁涂层,表面的污染物或灰尘能在重力或雨水、风力等外力作用下自动脱落或被降解的一种表面。给用户提供了有力的清洁保障。

图3 3线剖面
根据概率积分法对各矿段上下表面分别计算,分析影响半径,如表1所示。根据表1计算结果,3线标高0 m以上矿体采空后引起的地表变形宽度L1=366.4 m。
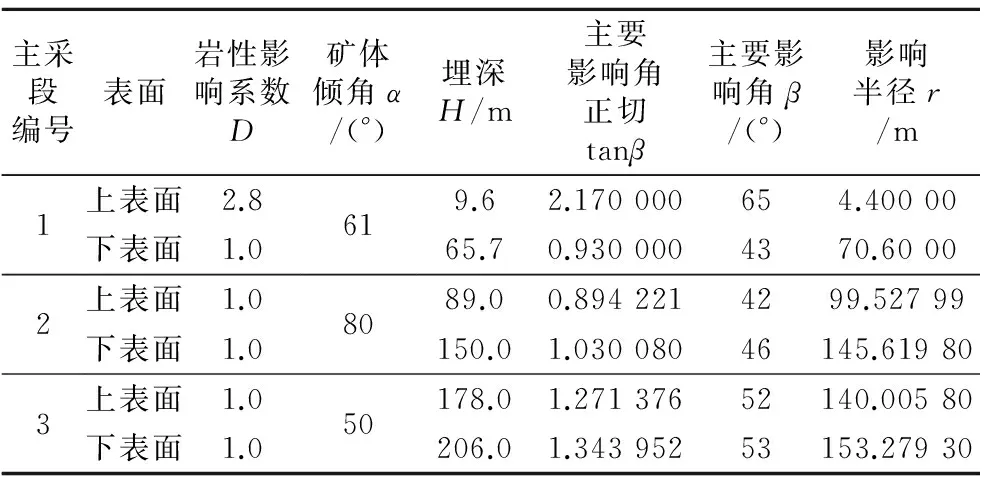
表1 3线剖面各矿段概率积分法计算
通过对各剖面图中集中矿段分别计算,可在地表划出各矿段采空后分别形成的沉降圈,绘出所有沉降圈的包络线,即为历史遗留空区引起地表沉降变形的最大范围。根据本文计算,该矿井下生产形成的地表沉降范围如图4所示。
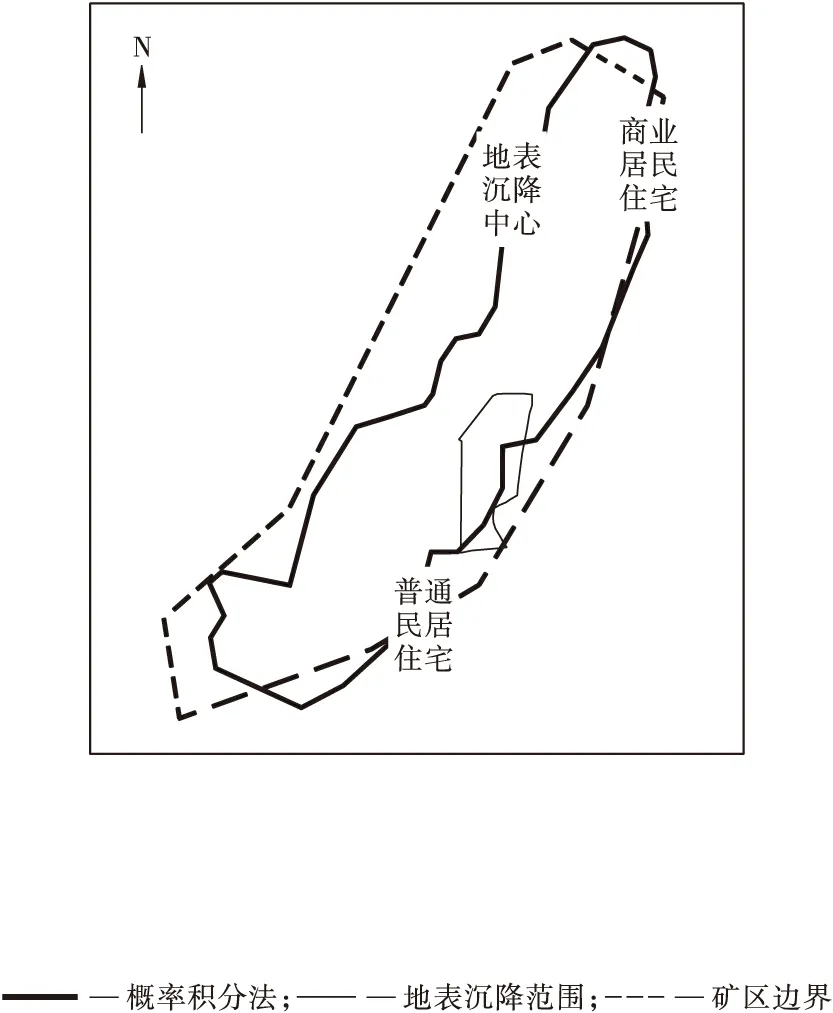
图4 概率积分法地表沉降范围
2.3地表建筑危险性判断
根据《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程》对建筑物保护等级及允许变形值的规定,采场影响范围内地表建(构)筑物按照重要性、用途和受影响后果的不同,可分为四级保护等级,对不同保护等级的地表建(构)筑物,应保证一定的保护带宽度,建(构)筑物外围保护带的宽度按照表2规定的数值选用。

表2 建筑物变形等级
根据式(2),矿区地表倾斜、曲率和水平应变分别为6.43 mm/m,0.446×10-3/m,4.13 mm/m,属移动带;但矿区边界处居民住宅区域的地表变形参数分别为0.08 mm/m,0.009×10-3/m,0.4 mm/m,计算结果符合变形等级I级要求。因此,依据概率积分法计算结果,矿区内及周边地表建筑较为安全,采矿活动不会对其稳定性产生影响。
3 FLAC数值模拟验证
为了验证概率积分法计算结果的合理性,使用有限差分法软件FLAC进行了数值模拟研究。由于该矿结构复杂,分布有大量零星矿段,建模较为复杂,因此仅对主体矿段进行研究。建成的FLAC模型尺寸为2 500 m×1 300 m×630 m,包含2个地质地层,3个计算组即大理岩、闪长岩和矿体,模型总计267 534个三维计算单元,48 685个网格节点。数值模拟模型如图5所示。

图5 FLAC数值模拟模型
根据该矿矿房矿柱布置方案,矿房高度为5 m,模拟5 m分段回采,0 m以上矿段采空并迭代稳定后模型地表产生了大面积沉降,如图6所示(沉降值单位为mm)。

图6 数值模拟地表沉降分布
由于近地表部分零星矿体没有反映在模型中,数值模拟中地表沉降量与实际情况有所出入,但沉降变化趋势和分布规律与实际情况基本吻合,矿区内塌陷坑的位置与数值模拟最大沉降量位置对应,表明数值模拟模型具有较高可信度。
在FLAC模型中,观测地表勘探线3线剖面中标高0 m以上矿体采空后的沉降发育,如图7所示(沉降值单位为mm)。经测量,3线剖面标高0 m以上矿段采空后引起的地表沉降宽度 。
概率积分法与数值模拟方法对3线剖面矿段的计算表明,在开采引起的沉降范围计算上,数值模拟手段更加趋于保守,沉降范围更大;此外,对比图4与图7可以看到,矿区东北侧与南部居民住宅都大部分位于概率积分法沉降范围外,数值模拟沉降范围之内,表明该区域可能出现了一定的沉降,但沉降量极小,该区域宽度d=180 m,计算得到地表倾斜为i=0.11 mm/m,符合规范。
4 地表沉降变化趋势分析
矿区内布设的地表沉降监测点基本覆盖了矿区大部分位置,尤其对东北部靠近商业居民住宅处进行了重点监测,监测工作从2012年持续至今,积累了大量的数据。将监测所得地表沉降数据使用Origin软件进行直线拟合,得到各监测点沉降量变化函数。21号监测点数据及拟合方程如图8所示。

图7 勘探3线剖面矿段采空地表沉降范围
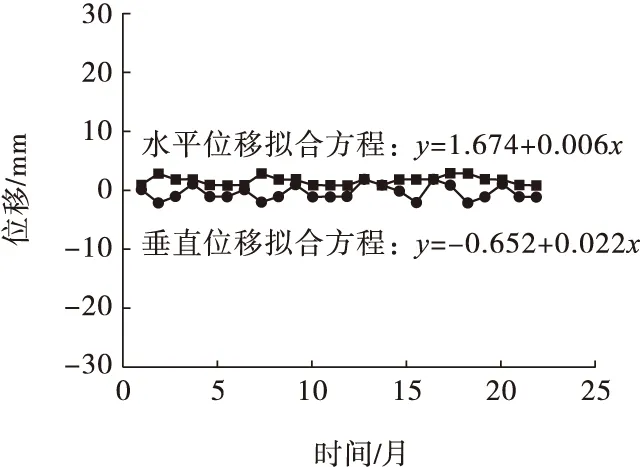
图8 21号监测点位移及拟合方程
该点沉降量拟合方程斜率极小,随着时间推移,该点沉降量基本不会变化。因此,可以认为该处地表沉降稳定,基本不受井下充填采掘活动影响。其他监测点沉降预测如表3所示。
通过对地表监测点沉降量的预测分析,可以看到,该矿区虽因早期使用崩落法开采,导致地面沉降变形较大,但经改进生产工艺,充填处理空区,且采掘深度逐渐加深后,井下生产对地表沉降影响更小,沉降量趋于稳定[10],不会对地表建筑物产生影响。
5 结 论
(1)理论计算与数值模拟结果都符合相关规定中的限定值,表明井下生产活动不会对矿区内及周边民居建筑稳定性产生影响。随着采深逐渐增大,近几年来的监测数据表明了地表稳定,没有发生较大规模的沉降量的变化。
(2)概率积分法使用由岩石坚硬程度决定的岩性影响系数D综合反映覆岩性质对沉降传播的影响。覆岩岩性为单一大理岩,但地表覆盖有较大厚度的地表土,二者性质差别大,可能导致D取值存在较大误差,影响概率积分法计算准确程度。因此,使用数值模拟手段进行了修正,事实证明,数值模拟计算结果趋于保守。
表3其他测点竖向沉降变形预测
Table 3Subsiding forecast of other monitoring points mm

监测点变 形 量2015年6月2016年6月2017年6月2018年6月2019年6月2020年6月精度(残余误差平方和)10#0.614041.228081.842122.456163.07023.684240.0604315#0.128520.257040.385560.514080.64260.771120.0498720#0.026040.052080.078120.104160.13020.156240.0395721#0.266040.532080.798121.064161.33021.596240.0372322#0.485160.970321.455481.940642.42582.910960.0404323#0.441000.882001.323001.764002.20502.646000.08626
(3)目前对于地表沉降量及沉降范围的研究方法众多,但大部分理论都基于特定假设,并对相关参数简化选取,可能导致最终结果与实际存在误差,因此,在实际运用中,应当运用多种方法论证,相互修正,确保研究结论的正确性。
(4)地表监测数据显示,近年来随着地下采矿作业采深增大,地表沉降趋于稳定,几乎没有变化,但计算结果表明,仍有一部分民居建筑位于数值模拟沉降范围内。因此,仍应继续沉降监测工作,同时继续改进充填工艺,保证安全生产,避免地表沉降对居民生活影响。
[1]张军胜,李俊平,宋士生.采空区处理新方法研究与应用[J].金属矿山,2009(8):19-22. Zhang Junsheng,Li Junping,Song Shisheng.Research and application of the treatment technology for abandoned slope[J].Metal Mine,2008(8):19-22.
[2]田泽军,周会志.对石人沟铁矿采空区处理方法的探讨[J].金属矿山,2008(12):157-159. Tian Zejun,Zhou Huizhi.Study of goaf governance methods for Shirengou iron ore[J].Metal Mine,2008(12):157-159.
[3]煤炭工业部.建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程[S].北京:煤炭工业出版社,2000. Ministry of Coal Industry.Buildings,Water,Railway and Main Well Lane of Coal Pillar and Coal Mining Regulation[S].Beijing:China Coal Industry Publishing House,2000.
[4]何国清,杨伦,凌赓娣,等.矿山开采沉降学[M].徐州:中国矿业大学出版社,1991. He Guoqing,Yang Lun,Ling Gengdi,et al.Mining Subsidence[M].Xuzhou:China University of Mining and Technology Press,1991.
[5]黄乐亭.开采沉陷力学的研究与发展[J].煤炭科学技术,2003,31(2):54-56. Huang Leting.Research and development of mining subsidence mechanism[J].Coal Science and Technology,2003,31(2):54-56.
[6]马海涛,刘宁武,王云海,等.金属矿山采空区灾害防治技术研究综述[J].中国安全生产科学技术,2014,10(10):75-80. Ma Haitao,Liu Ningwu,Wang Yunhai,et al.Review on research status of controlling techniques for goaf disaster in metal mine[J].Journal of Safety Science and Technology,2014,10(10):75-80.
[7]吴侃,靳建明,戴仔强.概率积分法预计下沉量的改进[J].辽宁工程技术大学学报,2003(2):19-22. Wu Kan,Jin Jianming,Dai Ziqiang.Improvement on probability integral method prediction come down quantity[J].Journal of Liaoning Technical University,2003(2):19-22.
[8]顾叶,宋振柏,张胜伟.基于概率积分法的开采沉陷预计研究[J].山东理工大学学报:自然科学版,2011(1):33-36. Gu Ye,Song Zhenbai,Zhang Shengwei.Research of mining settlement estimate based on probability integration[J].Journal of Shandong University of Technology:Natural Science,2011(1):33-36.
[9]陈雨,张振文,张彦敏.基于概率积分法的地面沉陷灾害预测[J].辽宁工程技大学学报,2007(11):143-144. Chen Yu,Zhang Zhenwen,Zhang Yanmin.Disaster prediction of surface subsidence based on probability integration[J].Journal of Liaoning Technical University,2007(11):143-144.
[10]耿德庸,仲惟林.用岩性综合评价系数P确定地表移动的基本参数[J].煤炭学报,1980(12):14-17. Geng Deyong,Zhong Weilin.Calculation of surface movement basic parameters with lithologic comprehensive evaluation coefficientP[J].Coal Engineering,1980(4):14-17.
(责任编辑徐志宏)
Study on the Ground Subsiding Area Caused by Underground Mining and Its Developing Tendency
Liu Shijie1,2,3Li Tie1,2Ma Haitao3,4Liu Sanping1,3
(1.SchoolofCivilandEnvironmentalEngineering,UniversityofScienceandTechnologyBeijing,Beijing100083,China;2.KeyLaboratoryofHigh-efficientMiningandSafetyofMetalMine,MinlstryofEducation,Beijing100083,China;3.ChinaAcademyofSafetyScience&Technology,Beijing100012,China;4.KeyLaboratoryonMiningGoafDisasterPreventionofSAWS,Beijing100012,China)
Combined with the probability integral method and numerical simulation,the effect that underground mining conduct on the residential buildings around is studied.Results show that the residential buildings are at the boundary of the mining subsiding area,the dipping,curvature and horizontal deformation of subsidence are 0.08 mm/m,0.009×10-3m,0.4 mm/m respectively,which are within the indexes given in related standards.The subsiding scope in numerical simulation is larger than that in probability integral method.Comparison of the subsiding scope at the same section shows that the subsiding width in numerical simulation is 407.6 m,larger than 366.7 m in probability integral method.Besides,fitting analysis on the subsiding monitoring data shows that the slope of the subsidence changing in recent years is less than 0.03,which means the ground subsiding tends to be steady and there is no new subsiding trend.Therefore,it is concluded that the residential buildings around will not be affected by the underground mining activities.It's found that error may occur in the choosing of the parameter reflecting the property of the overlying stratus,which lead to a difference between the results solved by probability integral method and numerical simulation.It's better to conduct studies in different ways to avoid error in dealing with problems in order to ensure the correction of the results and the harmony between underground mining and people's daily lives.
Probability integral method,Ground subsiding,Numerical simulation,FLAC
2015-07-22
刘诗杰(1992—),男,硕士研究生。
TD73
A
1001-1250(2015)-09-152-05

