饱和土体中衬砌隧道在移动荷载下的动力响应

曾 晨，孙宏磊，蔡袁强，3，曹志刚

（1.浙江大学 滨海和城市岩土工程研究中心，浙江 杭州310058；2.浙江大学 软弱土与环境土工教育部重点实验室，浙江 杭州310058；3.温州大学 建筑与土木工程学院，浙江 温州325035）

随着地铁建设的快速发展，由地铁运营引起的振动及噪声问题日益严重，因此，亟需适当的振动评估方法来应对这些问题.

对于地铁引起的环境振动问题，目前已有许多分析模型和计算方法.Balendra等［1］利用二维有限元分析模型建立了“地铁-地基土-结构”体系，计算分析了一幢银行建筑在地铁振动下的稳态振动.Gardien等［2］开发了隧道振动的三维有限元模型，模型中包含3个子模型，考虑了从振动产生到向外传播的整个过程.Sheng等［3］采用“离散波数法”建立了一个预测模型，计算成层土中的圆形隧道（有衬砌或无衬砌）中作用固定或移动简谐荷载所引起的动力响应.Forrest等［4-5］提出了Pipe-in-pipe（PiP）模型，并结合双梁无渣轨道模型，用解析的方法研究了全空间中隧道的动力响应问题，考虑了轨道系统、衬砌结构与地层三者的耦合.Clouteau等［6］建立了三维模型计算地铁引起的自由场振动，用有限元和边界元分别模拟隧道和土体，研究了隧道和土体间的动力相互作用.Gupta等［7］比较了PiP模型和周期性有限元-边界元耦合模型，分别用这两种模型分析全空间中衬砌隧道的动力响应，所得结果的一致性很好.刘维宁等［8］建立“车辆-轨道基础-衬砌结构-地层系统”的三维有限元分析模型，对地铁列车引起地面振动响应进行了计算分析.谢伟平等［9］利用有限元方法分析了地铁运行时土体的波动特性，简化了列车荷载，并且考虑了地基土性质不同带来的影响.Bian等［10］采用2.5维有限元模型分析隧道与周围土体的相互作用，通过与半解析解的对比验证了本文模型的正确性；计算了地铁列车引起的土体振动，并分析了移动荷载振动频率对地表处波衰减的影响.以上各研究无论采用数值模拟还是解析方法，都是将土体用单相介质来模拟进行研究的.然而，富水地区地下水位较高，很多时候地铁隧道位于地下水位以下，将土体视为饱和两相介质更接近实际情况.已有的移动荷载动力响应的研究表明，当荷载移动速度接近地基土Rayleigh波波速时，用单相介质模拟饱和土体将带来较大的误差，无法准确预测整个体系的动力响应［11］.

其他一些学者则用饱和多孔介质模型来模拟土体，考虑流、固耦合作用，研究隧道结构与饱和土体的动力相互作用.Senjuntichai等［12］引入Biot饱和多孔介质模型，通过Laplace变换得到了全空间饱和多孔弹性介质中无限长隧道（无衬砌）内表面作用轴对称荷载的瞬时响应解答.Hasheminejad等［13］假设衬砌与周围饱和土体不完全连结，研究了轴对称环形移动荷载作用下的无限长圆形衬砌及周围土体的动力响应，并重点研究了衬砌与土体不完全连结带来的影响.刘干斌等［14］引入一种黏弹性本构模型，研究了无限黏弹性饱和多孔介质中圆柱孔洞（有衬砌）内表面受轴对称简谐荷载和流体压力作用时的频域响应问题.Lu等［15］研究了饱和土中隧洞（无衬砌）内表面作用移动轴对称荷载时的动力响应，并讨论了移动荷载的速度对隧洞动力响应的影响.黄晓吉等［16］通过引入势函数，研究了饱和土中圆形衬砌隧洞在环形移动荷载作用下的动力响应，计算并比较了3种隧洞模型的动力响应.虽然以上研究中都将土体视为饱和多孔介质，但都是使用轴对称或者平面应变模型进行分析，显然采用三维模型来模拟地铁隧道和周围土体的动力响应更符合实际.

本文采用无限长圆柱壳模拟衬砌，采用Biot饱和多孔介质模型［17-18］模拟衬砌周围土体，以解析方法研究了饱和土体全空间中圆形衬砌隧洞在沿轴向移动的径向单位点荷载作用下的三维动力响应.引入两类势函数来表示土骨架和孔隙水的位移，在不同环向模态下利用修正Bessel方程来求解各势函数，结合边界条件，得到频率-波数域内位移及孔隙水压力的解答.最后进行双重Fourier逆变换得到时间-空间域内的响应解.计算了隧道衬砌及周围土体响应的空间分布及频谱曲线等，并根据结果分析了荷载速度、土体渗透性等对土体和衬砌位移响应及土体孔压的影响.

1 衬砌结构振动方程

采用无限长圆柱壳模拟衬砌，衬砌的三维模型以及所采用的圆柱坐标系统见图1，衬砌在轴向χ、环向y、径向z的振动方程如下［4，19］：

式中：E、ρ、ν分别为衬砌的弹性模量、密度、泊松比；a为衬砌圆柱壳中面的半径；h为衬砌厚度；θ为环向角度（图1）；u、υ、w为衬砌中面沿χ、y、z方向的位移；qχ、qy、qz表示衬砌中面沿χ、y、z方向的净应力，等于作用在衬砌内、外表面荷载所产生应力的差值.位移及应力分量的正方向见图1.

当荷载作用线位于θ=0平面内时，各应力、位移分量可以展开成如下求和形式［4，20］：

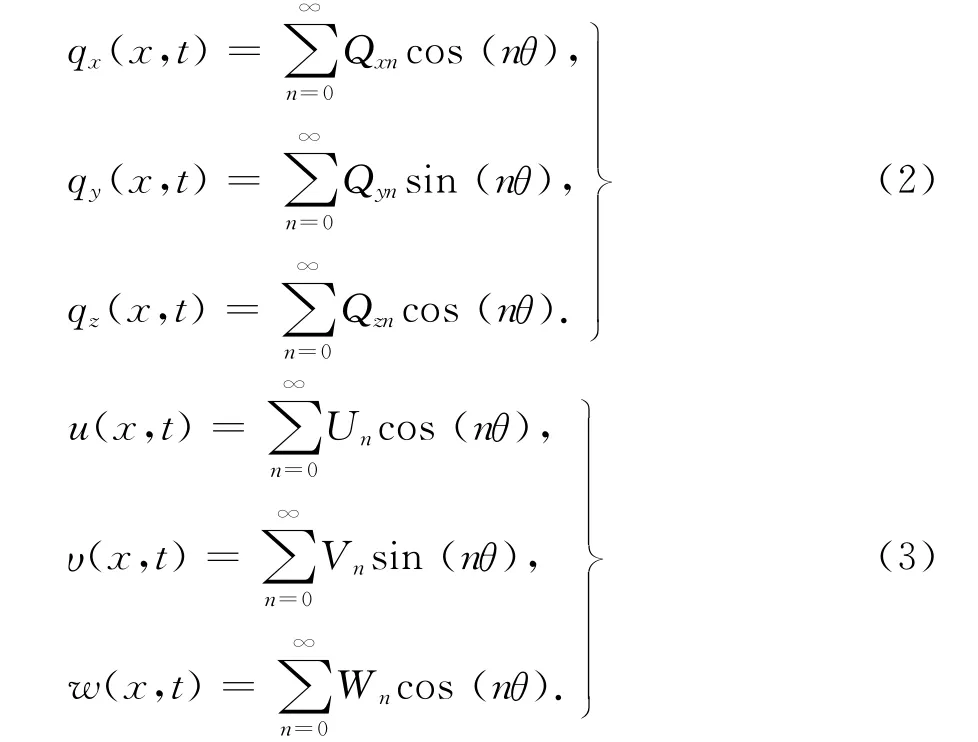
定义函数f（χ，t）关于坐标χ和时间t的双重Fourier变换及其逆变换为

将式（2）、（3）代入式（1a）～（1c），并使用式（4a）进行双重Fourier变换，可得频率-波数域内不同环向模态n下振动方程的矩阵形式：

式中：~Qχn、~Qyn、~Qzn、~Un、~Vn、~Wn是式（2）、（3）中各变量在频率-波数域内的对应量，A为3×3的矩阵.

2 饱和土体运动方程

本文认为衬砌周围土体为均质饱和多孔介质，引入Biot波动理论［17-18］：

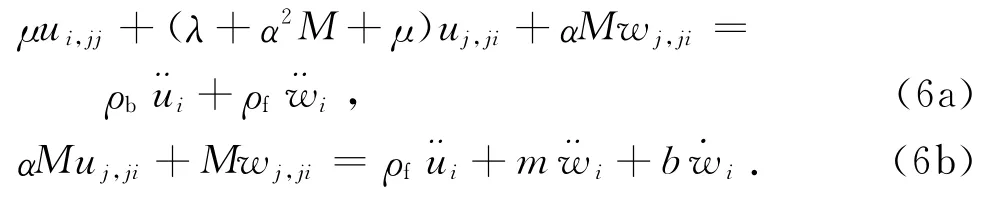
式中：ui、wi分别为土骨架位移分量和流体相对于土骨架的位移分量；¨ui、¨w i表示对时间t求导；λ、μ为土骨架的Lamé常数；α、M为表征土颗粒和流体压缩性的常数；b=η／kp为反映黏性耦合的参数，其中η、kp分别为流体的动力黏滞系数和土的动力渗透系数；ρb=n0ρf+（1-n0）ρs，其中n0为土体的孔隙率，ρf、ρs分别为流体密度和土骨架密度；m=ρf／n0.

均质饱和多孔介质的物理方程为

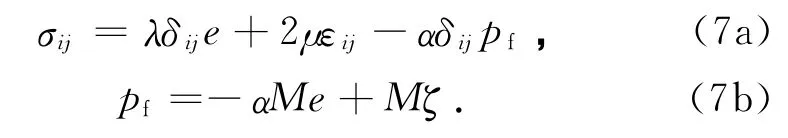
根据矢量场的Helmholtz分解定理，可以把式（6a）、（6b）中土骨架位移u和流体相对于骨架的位移w用标量势和矢量势表示为

将式（8）代入波动方程（6a）、（6b），并对时间t做Fourier变换，可以得到

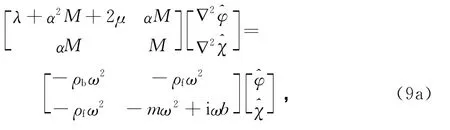
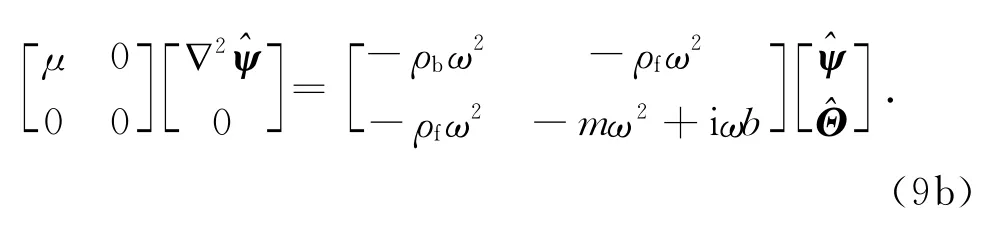
由式（9a）、（9b）可得如下 Helmholtz方程：

式中：kf、ks和kt分别代表饱和土中快纵波、慢纵波和横波的复波数，可表达为

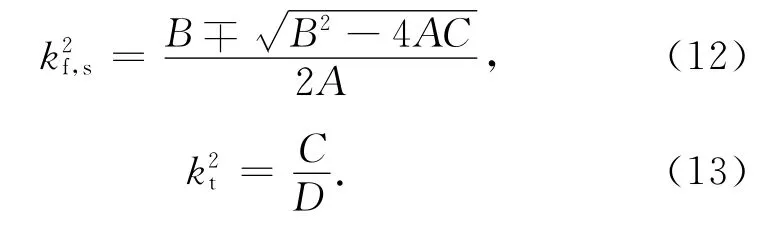
利用式（9）～（13），经推导整理，频域内的各势函数可表达为

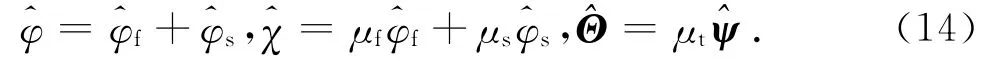
式中：

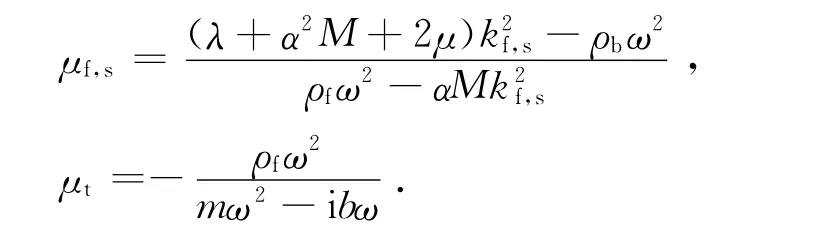
其中：

衬砌周围的全空间饱和土体三维模型及所采用的圆柱坐标系统见图2，土体的内径为2a（与图1中衬砌匹配），外径无穷大，并且沿轴向无限延伸.

在圆柱坐标系统 （r，θ，z）中，式（10）、（11）中的Laplace算子可表达为［4］

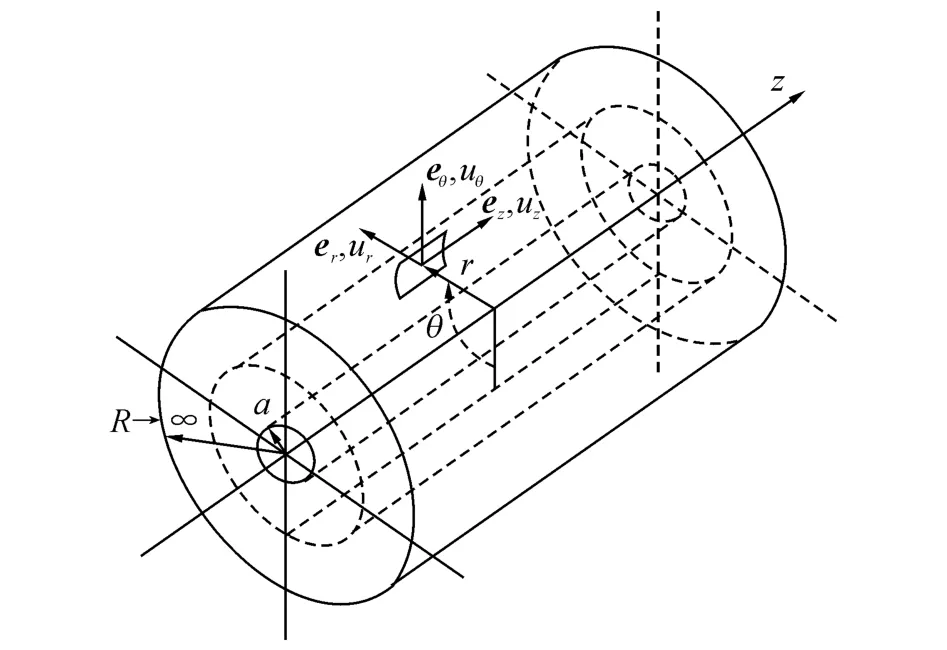
图2 衬砌周围饱和土体的三维模型Fig.2 Three-dimensional model for saturated soil surrounding liner

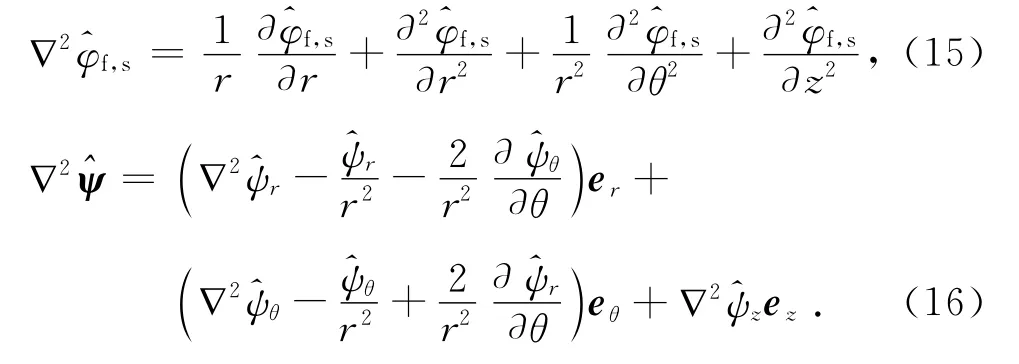
式中：er、eθ、ez分别是沿圆柱坐标系主方向r、θ、z的单位向量，是的分量.

展开式（8），再利用式（14）可将土骨架沿r、θ、z方向的位移分量用势函数表达为

为了求解方程（10）、（11），类似于式（2）、（3），可设各势函数具有如下形式：

将式（15）、（16）、（18）代入式（10）、（11），做关于坐标z的Fourier变换，在不同模态n下可得

式（19a）中的求导符号表示对r求偏导.

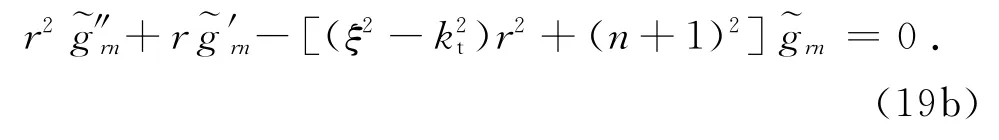
式（19a）中的第1、2、5式为n阶修正Bessel方程，而式（19b）为n+1阶修正Bessel方程，这4个方程的解具有如下形式：

将式（18）代入式（17），对坐标z做Fourier变换，并注意到~gθn=-~g rn，不同模态n下各位移分量可进一步表达为

对物理方程（7a）、（7b）取关于时间t的Fourier变换，变换后对其中2项进行如下操作：

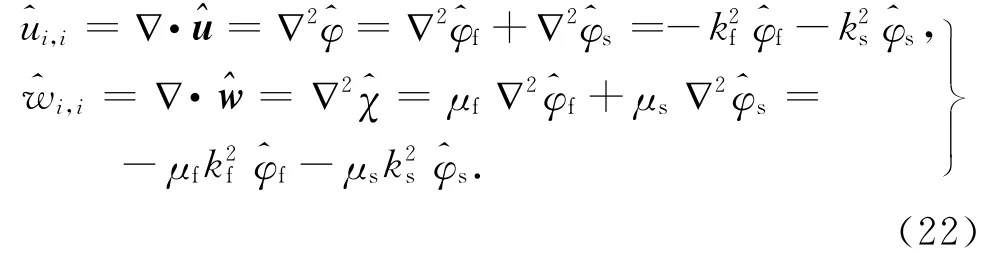
使用圆柱坐标系下的几何方程，得孔压和各应力表达式：

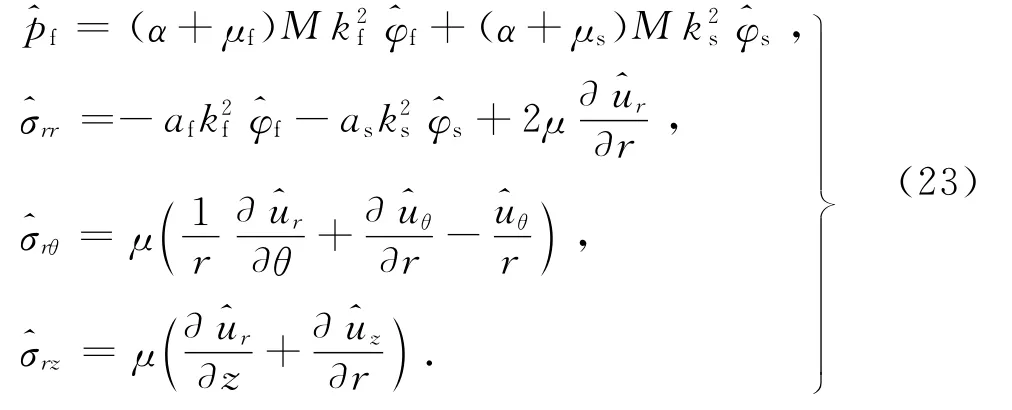
将式（18）、（21）代入式（23），对坐标z做Fourier变换，孔压和各应力在不同模态n下可进一步表达为

将式（20）分别代入式（21）、（24）中，利用修正Bessel函数的递推关系［4］进行整理，可得不同模态n下，饱和土体的土骨架位移及总应力在频率-波数域中的矩阵表达式：

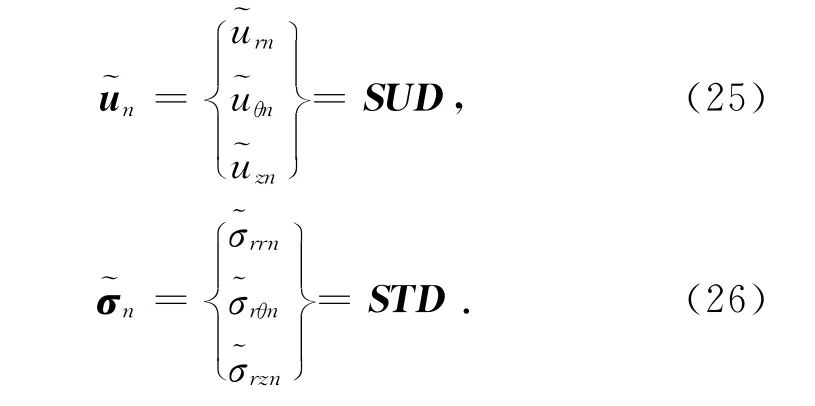
式中：U和T均为3×8的矩阵，这2个矩阵中第i行、第j列的元素分别为u ij、tij；

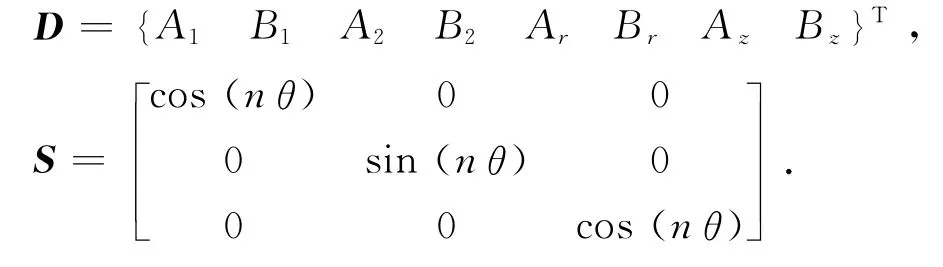
比较式（25）、（26）与式（2）、（3）可知，~un和~σn的各分量在不同的环向模态数n下可表达为

3 衬砌与周围饱和土体的相互作用

为研究隧道衬砌与周围饱和土体的相互作用，引入如下的边界条件［4，13］：

1）衬砌壳体的净应力等于荷载引起的衬砌内、外表面应力的合应力；

2）衬砌与饱和土体接触面处位移、应力连续；

3）衬砌与饱和土体接触面完全不透水；

4）距离荷载作用点无限远处的位移衰减为0.

如图1所示，在衬砌内表面的θ=0（仰拱）处作用一个沿χ正方向移动的、幅值恒定的径向单位点荷载.该荷载移动速度为v0，在t=0时位于χ=0位置，它在χ、y、z方向产生的分量表达如下：

式中：δ（·）为狄拉克δ函数.

将式（28）中的δ（θ）／a展开为 Fourier余弦级数［4］，并做关于χ和t的双重Fourier变换，得不同模态n时该荷载在频率-波数域内的各分量为

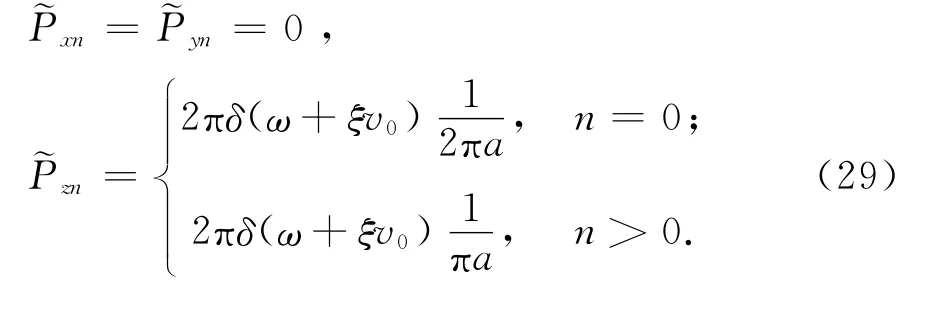
根据第1个边界条件，由式（5）有，在衬砌与饱和土体接触面处

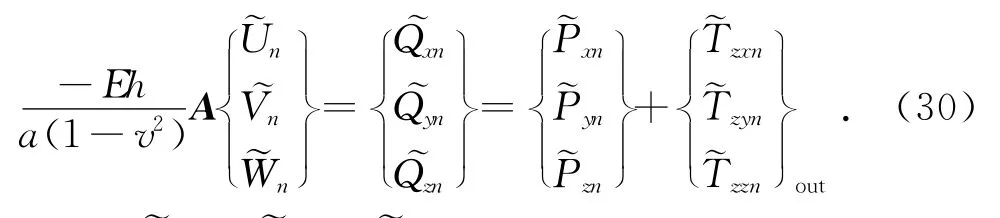
比较图1和图2所采用的圆柱坐标系，根据第2个边界条件，得到如下关系：

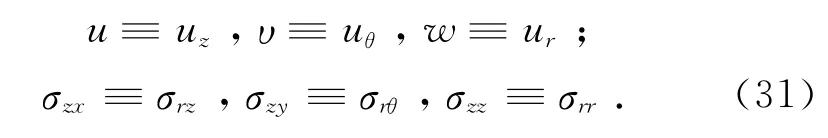
式中：σzχ、σzy、σzz分别为图1坐标体系下的应力，不同模态n时它们在频率-波数域内对应的量即为

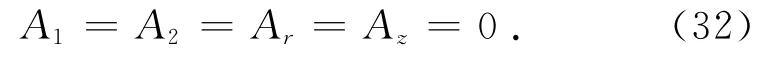
同时利用式（31）、（32），可得衬砌与饱和土体接触面处的位移、应力表达如下：

将式（33）、（34）代入式（30）中，有

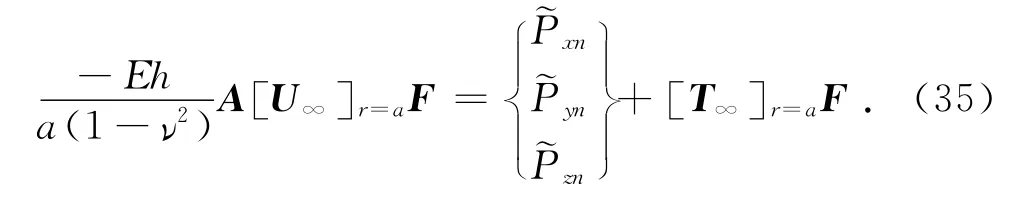
结合式（32），展开式（24）中~pfn的表达式，在不同模态n下有

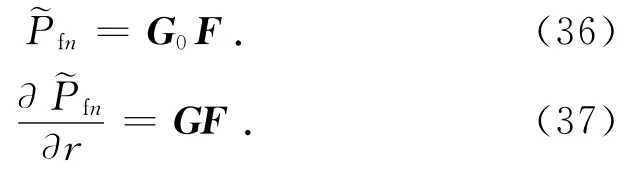
式中：G0及G均为1×4的矩阵.根据第3个边界条件，有

联立式（35）、（38），有

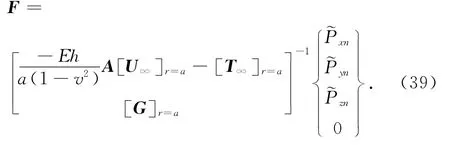
再联立式（33）、（36），解得不同的环向模态数n下r=R（R≥a）处的位移、孔压：

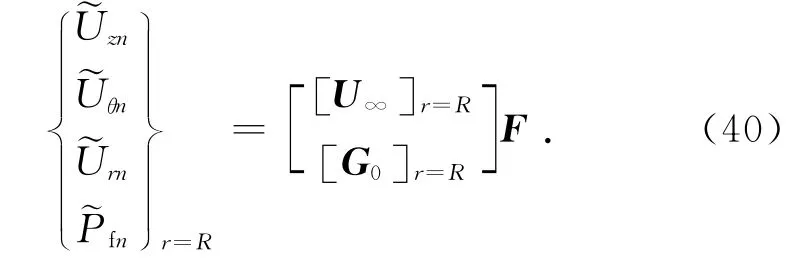
最后进行关于ξ和ω的双重Fourier逆变换，可得饱和土体中点（r，θ，z）处在时间-空间域内的土骨架位移分量、孔压表达式

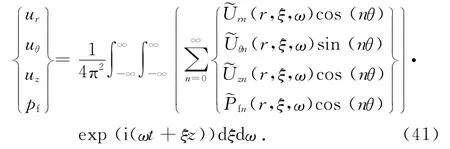
当r=a时，u r、uθ、u z同时也表示衬砌中面的位移.

由式（29）、（39）可知，待定系数矩阵F中各元素均含有一个相同的项2πδ（ω+ξv0），若令~P zn=，进行类似操作，式（41）可进一步简化为

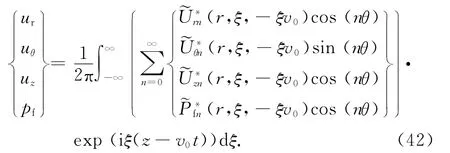
令z0=z-v0t，则式（42）中所求各分量变成与时间无关的量.也就是说，在随点荷载一起移动的坐标系（r，θ，z0）下，本文研究的问题变成了一个稳态问题.

4 算例与分析

4.1 与以往解析解的对比

为验证本文方法的正确性，采用本文方法计算了文献［13］中荷载移动速度v0=10 m／s、土体为硬土（Stiff soil）时的径向位移ur.文献［13］中衬砌内作用的是一个恒定的环形移动荷载，因此，在计算时，将环形荷载等效成180个沿圆周均匀分布的点荷载，将每个点荷载在考察点处引起的位移进行叠加，所得结果见图3.从图3可以看出，二者结果吻合得很好，验证了本文方法的正确性，同时也说明采用圆柱壳来模拟隧道衬砌的精度是足够的.

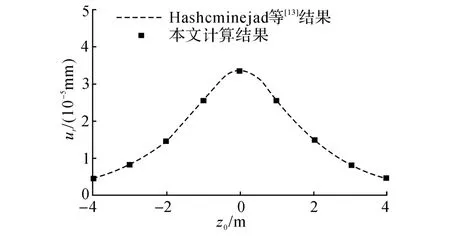
图3 本文与Hasheminejad等[13]的结果对比Fig.3 Comparison between present work and Hasheminejad's［13］work

4.2 参数分析

本节各算例中所采用的模型参数为：衬砌参数来自文献［4］，取E=5×1010Pa，ρ=2 500 kg／m3，ν=0.3，a=3 m，h=0.25 m；饱和土体参数则参考了文献［21］，取Lamé常数λ=3×107Pa，μ=2×107Pa，ρf=1 000 kg／m3，ρs=2 600 kg／m3，n0=0.4，α=1.0，M=5×109Pa，b=106～1010N·s／m4.移动荷载的幅值为1 N.

图4给出了当土体b值不同时，移动荷载作用点以及正下方3 m处（即r=3 m和6 m，θ=0，z0=0）的径向位移ur随荷载移动速度v0变化的曲线.为了比较，图4中还给出了单相弹性土体中对应的位移曲线，计算时将饱和土体参数ρf、b、α、M、m取为10-4，使得饱和土体退化为单相弹性土体［22］.

从图4可以看到，与地面交通系统类似［11］，饱和土体中衬砌隧道系统也存在临界速度（临界速度即为图中各曲线峰值所对应的v0值）.当v0＜30 m／s时，各条曲线均比较平缓，位移ur随v0变化的影响很小，此后ur随v0增大而迅速增大，并在达到峰值后又迅速减小.图4中的各条曲线均在v0=102 m／s附近时达到峰值，与土体中的S波波速（弹性土体及无渗流的饱和土体的S波波速均为vs=101 m／s）非常接近.图4（a）中各曲线明显大于其在图4（b）中对应的曲线.由图4（a）可知，饱和土体中荷载作用点处的ur随着土体b值的增大（土体渗透性变差）而减小，并且均小于相应的弹性土体中的ur.图4（b）中，荷载正下方3 m处的饱和土体ur则随着土体b值的增大而增大，3个b值相对应的u r曲线中仅有b=106N·s／m4时的ur小于弹性土体中的u r.

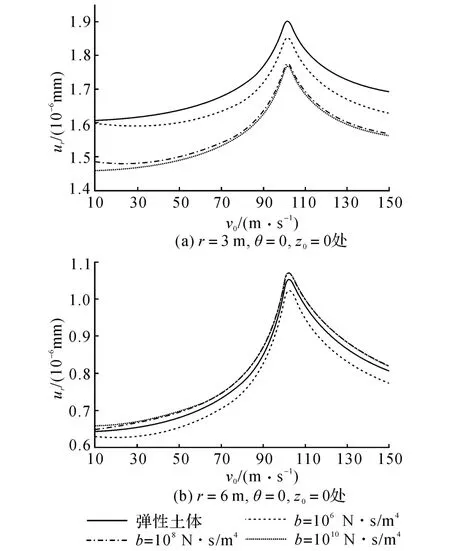
图4 不同b值时荷载下方两点的u r随v 0变化的曲线Fig.4 ur of two points varied with v0 for different b

鉴于图4中2点的位移ur受b值变化影响的规律不同，图5给出了当v0=105 m／s时荷载正下方处（θ=0，z0=0）的土体响应沿径向坐标r的分布曲线.图5（a）中各条ur曲线均随着r的增大而迅速减小.在衬砌附近（r＜4.5 m）的土体中饱和土体ur随着土体b值的增大而减小，并且均小于弹性土体ur；当r＞4.5 m时，饱和土体ur随着土体b值的增大而增大，并且b值较大（土体渗透性较差）时的饱和土体ur大于弹性土体u r.本文的公式推导中认为衬砌与土体接触面完全不透水，接触面处流体与土骨架的运动是完全一致的，由于流体的压缩模量很大，衬砌附近饱和土体的压缩刚度大于相应弹性土体的刚度，因此，衬砌附近饱和土体ur小于弹性土体u r.

本研究中的点荷载沿着轴向移动，其所引起的整个系统的响应不是关于z0=0平面对称（静止荷载引起的响应才是对称的），因此，荷载正下方土体骨架的轴向位移u z并不为0.u z沿径向r的分布曲线见图5（b），随着r的增大，各u z曲线均先增大后减小.土骨架u z随着土体b值的增大而迅速减小，当b=1010N·s／m4时，u z已基本接近0，但是仍然大于弹性土体的u z.移动荷载下方饱和土骨架的轴向位移要大于弹性土体中的轴向位移，若采用弹性模型来模拟隧道周围土体会低估此处轴向位移.

图5 v0=105 m/s时荷载正下方处的响应沿r的分布曲线Fig.5 Response of points under moving load varied with r when v0=105 m／s

根据图5（c），随着r的增大，各pf曲线呈现减小趋势，在r＞9 m后基本重合.孔压pf随着b值的增大而增大，渗透性差的土体在荷载作用点附近会产生较大的孔压.

图6给出了v0=10 m／s和v0=105 m／s时隧道仰拱（r=3 m，θ=0）以及仰拱下方3 m（r=6 m，θ=0）处的径向位移ur沿轴向坐标z0的分布.图中仍然给出了单相弹性土体中对应的曲线.可以看到，由于v0=105 m／s更接近临界速度，此时的ur曲线大于v0=10 m／s时的ur曲线.各条ur曲线的形状类似，均在荷载作用平面（z0=0）附近出现峰值，基本呈现对称的分布.仰拱处ur曲线的形状更为尖锐，并且要远大于仰拱下方3 m处的曲线.

图6 不同b值时隧道仰拱以及仰拱下方3 m处的ur沿的分布曲线Fig.6 ur of tunnel invert and points 3 m under the invert varied with z0 for different b

与图4（a）类似，由图6（a）、（b）可以看到，饱和土体中的仰拱位移ur随着土体b值的增大而减小，并且均小于弹性土体中的ur.在图6（c）、（d）中，靠近z0=0平面的饱和土体的土骨架位移ur随着b值的增大而增大，|z0|增大后则随着土体b值的增大而减小；在z0=0平面附近，仰拱下方3 m处弹性土体的ur小于b=108N·s／m4时的ur.随着|z0|的增大，位移ur中由S波引起的部分所占的比例也在增大，饱和土体中流体的存在使得饱和土体中S波衰减的更快，因此，正如图6中所见，弹性土体ur又大于饱和土体u r了.

图7给出了当v0=10 m／s和v0=105 m／s时隧道仰拱下方3 m（r=6 m，θ=0）处的轴向位移u z沿轴向坐标z0的分布，各条曲线基本呈现反对称的分布.当v0=105 m／s时的uz曲线略大于v0=10 m／s时的u z曲线，但增大幅度不如图6（c）、（d）中的ur曲线.饱和土体uz随着土体b值的增大而增大，并且均大于弹性土体u z.随着|z0|的增大，各条u z曲线先增大后减小，减小的同时有重合的趋势.

结合图6、7可以看到，b=108N·s／m4时的曲线与b=1010N·s／m4时的曲线很接近，荷载高速移动（v0=105 m／s）时更是基本重合，说明当衬砌周围土体是渗透性较差的黏性土时，b值的变化对位移响应的影响很小.此外，图6、7的各位移分布曲线中，弹性土体曲线的对称性（包括反对称性）最好，b=106N·s／m4曲线的对称性最差；当v0=105 m／s时位移分布对称性比v0=10 m／s时差.饱和土体和弹性土体中的位移响应区别明显，饱和土体位移场的对称性受荷载速度、土体渗透性影响较大.

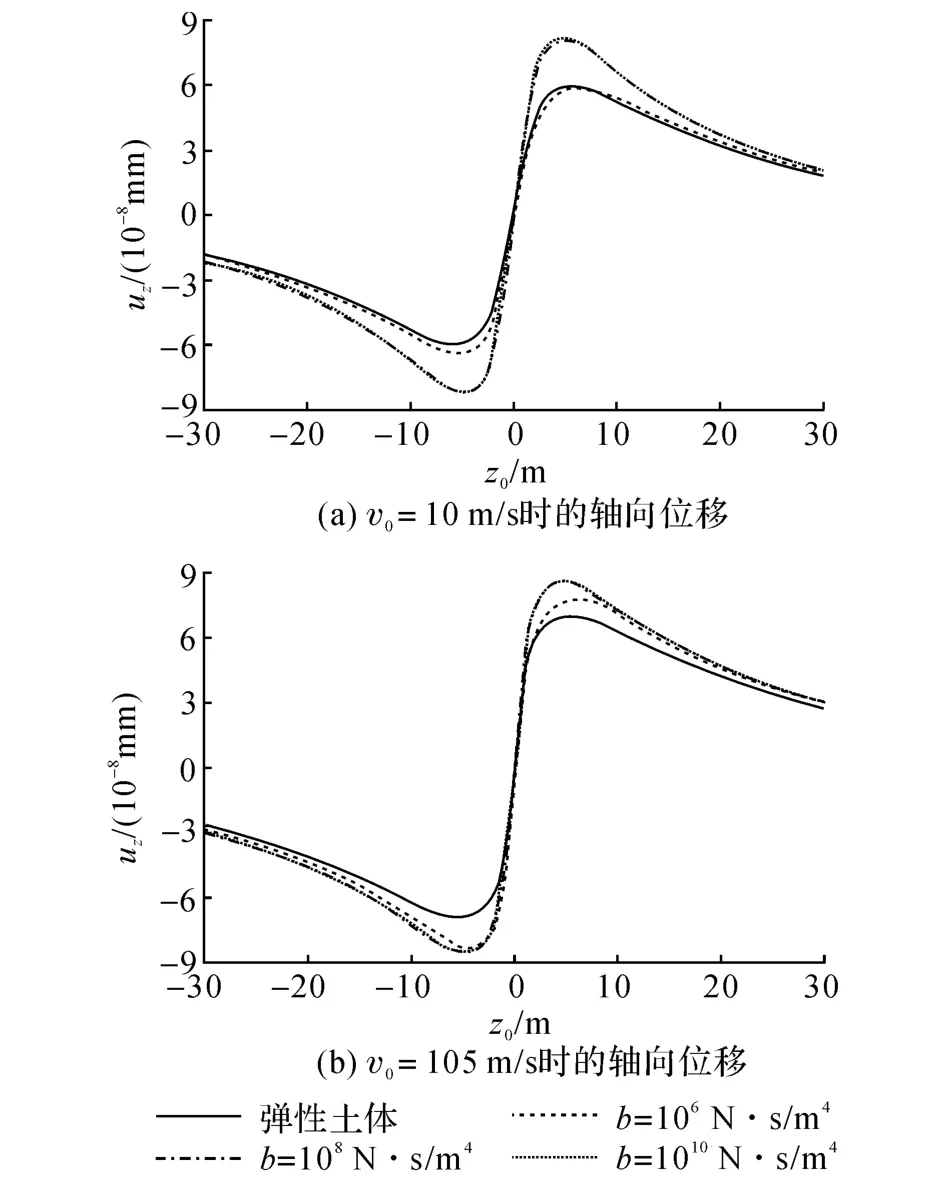
图7 不同b值时隧道仰拱下方3 m处的uz沿z 0的分布曲线Fig.7 uz of points 3 m under the tunnel invert varied with z0 for different b

图8给出了当v0=10 m／s和v0=105 m／s时隧道仰拱下方3 m（r=6 m，θ=0）处的土体孔压pf沿轴向坐标z0的分布，可以看到孔压最大值基本出现在荷载作用平面处.当b=106N·s／m4增大到b=108N·s／m4时，pf迅速增大，之后增大趋势减小.图8中当b=106N·s／m4时的2条曲线在z0=0附近及z0＞0区域内均大于0，而在z0＜0区域内小于0.可见在渗透性较好土体中，恒定移动荷载下方及下前方区域内孔压为正，下后方区域内孔压为负；渗透性较差的土体内则主要是正孔压，分布比较对称.当v0从10 m／s增大到105 m／s，b=106N·s／m4时的孔压曲线显著增大，而当b=108N·s／m4与b=1010N·s／m4时的曲线变化不大.渗透性较好土体的孔压受荷载移动速度v0的影响比较明显.

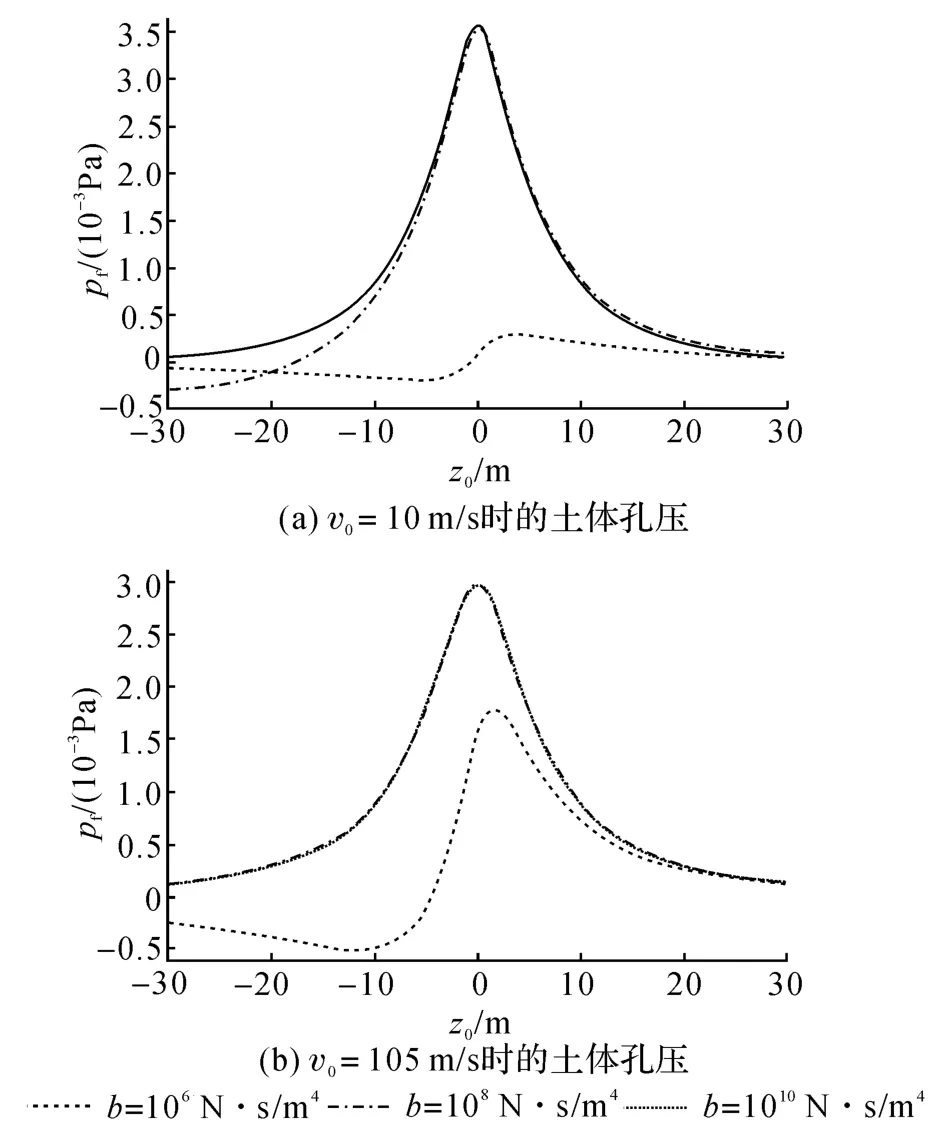
图8 不同b值时隧道仰拱下方3 m处的p f沿z0的分布曲线Fig.8 pf of points 3 m under the tunnel invert varied with z0 for different b

图9给出了当v0=10 m／s和v0=105 m／s时隧道仰拱下方一点（r=6 m，θ=0，z=0）处径向位移ur的频谱曲线，在t=0时刻移动荷载位于z=0平面上，频率f=ω／（2π）.可以看到，各条曲线均随着频率f增大而减小，v0的变化对频谱曲线的影响很大：v0=10 m／s时的频谱曲线比v0=105 m／s时减小得更快，v0=105 m／s时频谱分布的频率范围更大；当f较小时，v0=10 m／s的频谱值比v0=105 m／s时的大，当f超过一定值（约为0.35 Hz）后，v0=105 m／s的频谱值更大.

b值不同引起的u r频谱曲线的差别主要分布在低频范围，频率f越大各曲线越接近.在图9（a）、（b）的各条饱和土ur频谱曲线中，b=106N·s／m4的频谱值在低频时最大，随着f增大逐渐变成最小.在f较小时弹性土体中u r的频谱值大于饱和土体中u r的频谱值，f增大后则小于饱和土体中u r的频谱值.

图9 不同b值时一点处u r的频谱曲线Fig.9 Frequency spectrum of ur of a point for different b

5 结 论

本文用无限长圆柱壳来模拟衬砌，用Biot饱和多孔介质模型来模拟土体，以解析方法研究了饱和土体全空间中圆形衬砌隧道在移动点荷载作用下的三维动力响应.计算了隧道衬砌及周围土体响应的空间分布和频谱曲线等，并根据结果分析了荷载速度、土体渗透性等对位移响应及土体孔压的影响.得到如下结论：

（1）与地面交通系统类似，饱和土体中衬砌隧道系统也存在临界速度.临界速度与无渗流饱和土体的S波波速基本一致.

（2）饱和土体中的位移及孔压分布受荷载速度、土体渗透性影响较大.衬砌及衬砌附近（径向坐标r较小）的饱和土体骨架位移随耦合性参数值增大（土体渗透性变差）而减小；而离衬砌稍远处的饱和土体位移受耦合性参数值变化影响的规律较为复杂，还与荷载移动速度、观察点到荷载作用平面（z0=0）的轴向距离等有关.土体孔压随耦合性参数值增大而增大.但当衬砌周围土体为渗透性较差的黏性土时，耦合性参数值的变化对土体位移、孔压的影响比较小.

（3）衬砌附近饱和土体的位移小于弹性土体中的位移，而离衬砌稍远区域中荷载作用平面附近的饱和土体位移则大于弹性土体中的位移.荷载的移动性对饱和土体位移场对称性的影响要大于对弹性土体的影响，饱和土体和弹性土体中的位移响应区别明显，在富水地区研究地铁隧道及周围土体的动力响应问题时，应采用与实际情况更接近的饱和多孔介质模型模拟土体.

（4）荷载移动速度变化对土体位移频谱的影响很大，当速度由低速增大到接近临界速度时，频谱曲线分布的频率范围增大，高频成分明显增多，但低频时的频谱值明显变小.

（

）:

［1］BALENDRA T，CHUA K H，LO K W，et al.Steadystate vibration of subway-soil-building system［J］.Journal of Engineering Mechanics，1989，115（1）：145- 162.

［2］GARDIEN W，STUIT H G.Modelling of soil vibrations from railway tunnels［J］.Journal of Sound and Vibration，2003，267（3）：605- 619.

［3］SHENG X，JONES C J C，THOMPSON D J.Ground vibration generated by a harmonic load moving in a circular tunnel in a layered ground ［J］.Journal of Low Frequency Noise，Vibration and Active Control，2003，22（2）：83- 96.

［4］FORREST J A，HUNT H E M.A three-dimensional tunnel model for calculation of train-induced ground vibration［J］.Journal of Sound and Vibration，2006，294（4）：678- 705.

［5］FORREST J A，HUNT H E M.Ground vibration generated by trains in underground tunnels［J］.Journal of Sound and Vibration，2006，294（4）：706- 736.

［6］CLOUTEAU D，ARNST M.，AL-HUSSAINI T M，et al.Freefield vibrations due to dynamic loading on a tunnel embedded in a stratified medium ［J］.Journal of Sound and Vibration，2005，283（1／2）：173- 199.

［7］GUPTA S，HUSSEIN M F M，DEGRANDE G，et al.A comparison of two numerical models for the prediction of vibrations from underground railway traffic［J］.Soil Dynamics and Earthquake Engineering，2007，27（7）：608- 624.

［8］刘维宁，夏禾，郭文军.地铁列车振动的环境响应［J］.岩石力学与工程学报，1996，15（增刊）：586- 593.LIU Wei-ning，XIA He，GUO Wen-jun.Study of vibration effects of underground trains on surrounding environments［J］.Chinese Journal of Rock Mechanics and Engineering，1996，15（S）：586- 593.

［9］谢伟平，孙洪刚.地铁运行时引起的土的波动分析［J］.岩石力学与工程学报，2003，22（7）：1180- 1184.XIE Wei-ping，SUN Hong-gang.FEM analysis on wave propagation in soils induced by high speed train loads［J］.Chinese Journal of Rock Mechanics and Engineering，2003，22（7）：1180- 1184.

［10］BIAN X C，JIN W F，JIANG H G.Ground-borne vibrations due to dynamic loadings from moving trains in subway tunnels ［J］.Journal of Zhejiang University-SCIENCE A：Applied Physics and Engineering，2012，13（11）：870- 876.

［11］CAI Y Q，CAO Z G，SUN H L，et al.Dynamic response of pavements on poroelastic half-space soil medium to a moving traffic load ［J］.Computers and Geotechnics，2009，36（1／2）：52- 60.

［12］SENJUNTICHAI T，RAJAPAKSE R K N D.Transient response of a circular cavity in a poroelastic medium［J］.International Journal for Numerical and Analytical Methods in Geomechanics，1993，17（6）：357- 383.

［13］HASHEMINEJAD S M，KOMEILI M.Effect of imperfect bonding on axisymmetric elastodynamic response of a lined circular tunnel in poroelastic soil due to a moving ring load［J］.International Journal of Solids and Structures，2009，46（2）：398- 411.

［14］刘干斌，谢康和，施祖元.黏弹性饱和多孔介质中圆柱孔洞的频域响应［J］.力学学报，2004，36（5）：557-563.LIU Gan-bin，XIE Kang-he，SHI Zu-yuan.Frequency response of a cylindrical cavity in poro-viscoelastic saturated medium ［J］.Acta Mechanica Sinica，2004，36（5）：557- 563.

［15］LU J F，JENG D S.Dynamic response of a circular tunnel embedded in a saturated poroelastic medium due to a moving load［J］.Journal of Vibration and Acoustics，2006，128（6）：750- 756.

［16］黄晓吉，扶名福，徐斌.移动环形荷载作用下饱和土中圆形衬砌隧洞动力响应研究［J］.岩土力学，2012，33（3）：892- 898.HUANG Xiao-ji，FU Ming-fu，XU Bin.Dynamic response of a circular lining tunnel in saturated soil due to moving ring load［J］.Rock and Soil Mechanics，2012，33（3）：892- 898.

［17］BIOT M A.Theory of propagation of elastic waves in a fluid-saturated porous solid.I.Low-frequency range［J］.Journal of the Acoustical Society of America，1956，28（2）：168- 178.

［18］BIOT M A.Theory of propagation of elastic waves in a fluid-saturated porous solid.II.High-frequency range［J］.Journal of the Acoustical Society of America，1956，28（2）：179- 191.

［19］FLÜGGE W.Stresses in Shells（second edition）［M］.Berlin：Springer，1973.

［20］JONES S，HUNT H.Voids at the tunnel-soil interface for calculation of ground vibration from underground railways［J］.Journal of Sound and Vibration，2011，330（2）：245- 270.

［21］SHI L，SUN H L，CAI Y Q，et al.Validity of fully drained，fully undrained andu-pformulations for modeling a poroelastic half-space under a moving harmonic point load［J］.Soil Dynamics and Earthquake Engineering，2012，42：292- 301.

［22］SENJUNTICHAI T，MANI S，RAJAPAKSE R K N D.Vertical vibration of an embedded rigid foundation in a poroelastic soil［J］.Soil Dynamics and Earthquake Engineering，2006，26（6／7）：626- 636.