有限长激光脉冲在部分离化等离子体中的传播

柳剑鹏，刘明萍，陶向阳*，刘三秋

(1.江西师范大学 物理与通信电子学院，南昌330022;2.南昌大学 信息工程学院，南昌330031;3.南昌大学 物理系，南昌330047)

引 言

由强激光脉冲驱动的尾波场电子加速机制为实现小型化高能粒子加速器提供了新原理和新方法［1］。强激光在等离子体中的传播特性和许多前沿科技联系密切，如惯性约束核聚变研究［2-4］、激光等离子体加速器［5-7］、高次谐波的产生［8-10］、激光等离子体通道实验设计［11-12］等。由于衍射效应，激光在等离子体中传播一个瑞利长度后就会发散，而在许多应用中要求激光在等离子体中传播几个甚至几十个瑞利长度。激光在等离子体中传播时，部分离化的等离子体也会影响激光的稳定传播，如SPRANGLE等人指出的等离子体电子密度调制不稳定性，就是由于部分离化等离子体中束缚电子作用产生;特别是在部分离化等离子体中，由束缚电子作用产生的密度调制不稳定性会影响相对论成丝不稳定性［13-15］。2004年，激光尾波场电子加速在实验上取得了突破性进展，人们用TW激光器实现了背景等离子体电子的自注入，得到了几十兆电子伏特准单能电子束［16-18］;当电子束运动距离大于失相长度时，电子束减速失去能量，使得能散度变大［19］，是造成无法获得单能电子束的主要原因之一。激光脉冲稳定传播直接影响电子的自注入和加速过程，LEEMANS等人利用3.3cm长预等离子体通道引导的激光尾波场加速器，在实验中获得了GeV准单能电子束［20］。部分离化等离子体相对于完全离化等离子体研究前景更加广阔，其对激光的传播特性影响更为复杂。

在激光有质动力作用下，等离子体中将产生电子密度扰动，形成电子等离子体波，即尾波场［14］。该密度扰动可以分为横向和纵向两部分:横向部分使电子沿横向排开，可以形成等离子体密度通道，称为有质动力自通道效应，这种自通道效应不但能加剧激光的自聚焦，而且能用来导引其它激光传播［5］;纵向部分是有质动力对激光束传播的轴向密度扰动，可以诱导电子加速。目前，尾波场对有限长激光脉冲在部分离化等离子体中传播特性的影响还没有详细的研究结果。

本文中从激光场与尾波场的耦合方程组出发，考虑了由激光有质动力激发的尾波场和部分离化等离子体中的非线性极化强度等影响，采用变分法推导出尾波场对强激光在不完全电离等离子体中传播时的焦斑半径与脉冲宽度的演化方程组，经过数值解析的方法求解，分析了尾波场对激光自聚焦效应作用强弱的影响因素。

1 激光焦斑半径和脉冲宽度演化方程组

在稀薄的部分离化等离子体中，假定激光脉冲是沿着z方向传播线偏振激光，并取激光脉冲归一化矢势为:

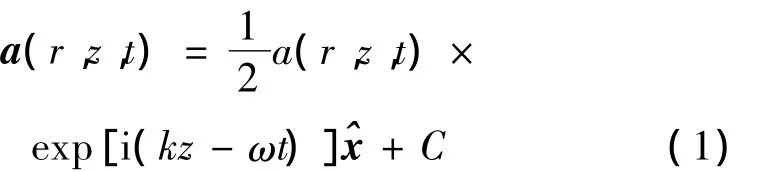
式中，r为激光半径，z为传播距离，t为激光传播时间，k和ω分别是激光的波数和频率，C表复数共轭，归一化矢势a=eA/(mc2)，A为激光场矢势，e为单位电荷量，m为静止状态下电子质量，c为光速，^x是沿x轴方向的单位矢量。

在库仑规范▽·a=0下，运动坐标系(z，ξ=zβgct)中，假定 a(r，z，ξ)为随激光传播的缓变包络复振幅，可忽略高阶衍射项∂2a/∂z2，其中，▽为哈密顿算子，βg为归一化群速度。激光脉冲在部分离化等离子体中传播的耦合方程组可约化为［20-21］:

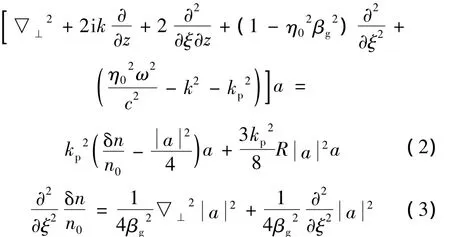
式中，R=Pa/Pp=8πχ3(mc/e)2ω4/ωp2是非线性极化强度，χ3是第3阶极化率，Pp是等离子体中的相对论激光临界功率，Pa是气体中非线性聚焦临界功率［20］，ωp是电磁场中等离子体振荡频率，δn/n0=(ne-n0)/n0是归一化等离子体密度扰动，ne是背景等离子体密度，n0是初始等离子体密度，η0是线性折射率，kp=ωp/c是等离子体波数。(2)式为激光场的波动方程，右边第1项包含真空衍射项，尾波场效应及相对论非线性影响，第2项是部分离化非线性效应;(2)式的左边第4项和第5项可通过对旁轴近似的修正得出，分别表示有限脉冲长度和群速度的色散效应。(3)式为等离子体密度扰动方程，即尾波场方程。

为了求解(2)式和(3)式，取激光脉冲为径向高斯包络的正弦函数，其复振幅a(r，z，ξ)的试探函数可设为［21］:

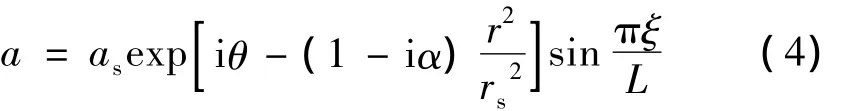
式中，α，θ，as，rs和 L 分别是激光波面曲率、相移、振幅、焦斑半径和脉冲宽度。将(4)式代入到(3)式，可得到等离子体密度扰动解析表达式，即激发的尾波场为:

对(2)式采用变分法求解，其Lagrangian密度为［21］:

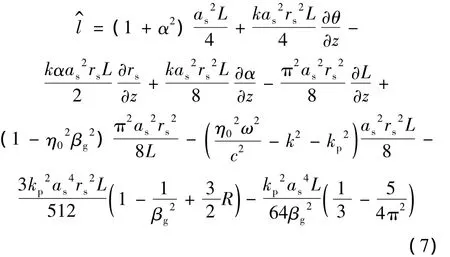
将(7)式分别对 as，α，rs，L 变分可以得到:

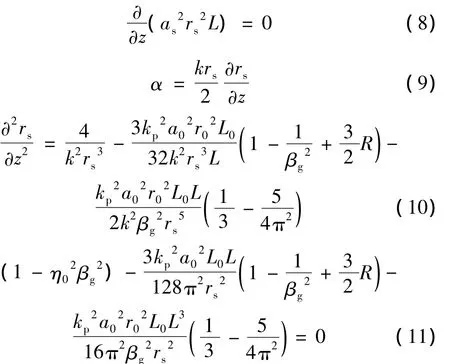
式中，a0，L0和r0分别是激光脉冲初始强度(z=0)、初始脉冲宽度和初始焦斑半径。在不考虑进一步电离的情况下，(8)式表示激光在部分离化等离子体中传播时功率守恒，且由其可知，(常数)。(9)式说明了波面曲率α与焦斑半径rs的关系。(10)式和(11)式是一个脉冲宽度L和焦斑半径rs关于激光传播距离z的演化方程组。(10)式右边第1项表示真空衍射对激光传播影响，第2项包括了相对论和部分离化等离子体的非线性自聚焦及激光的纵向有质动力激发的尾波场(longitudinal wakefield，LWF)对激光自聚焦效应的影响，第3项表示由激光的横向有质动力激发的尾波场(transverse wakefield，TWF)对激光自聚焦效应的影响，值得注意的是，LWF和TWF对激光脉冲都起聚焦作用。

引入归一化量 z～其中ZR=kr02/2为瑞利长度，取参量η0≈1，令Q=1-βg2。焦斑半径演化方程(10)式和脉冲宽度演化方程(11)式可简化为:

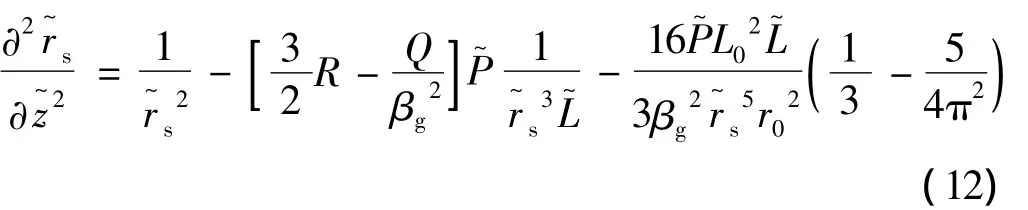
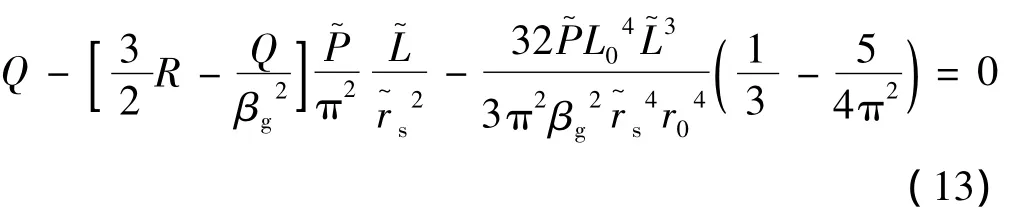
由(13)式可知，激光在部分离化等离子体中传播时初始脉冲宽度L0、初始焦斑半径r0、非线性极化强度R(归一化，无单位)以及等离子体密度n0不是独立的，必须满足一定的条件才能在其中传播，即有:

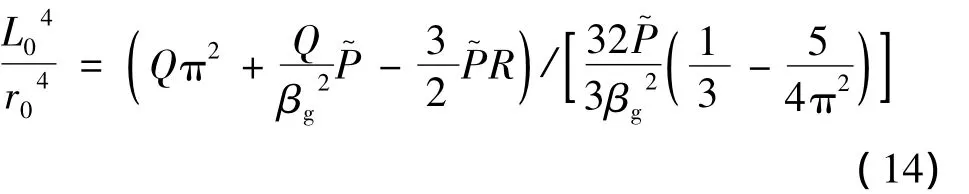
2 数值分析

现在可以通过微分方程(12)式和(13)式的解来描述强激光脉冲在部分离化等离子体中的传播特性，但由于该方程的高度非线性，求其解析解较为困难，可以通过4阶Runge-Kutta法进行数值求解。定义初始条件为:，激光和等离子体初始参量为:a0=0．02，n0=0．03nc，a0是脉冲激光初始强度，nc是等离子体临界密度。

将激光和等离子体初始参量代入(14)式可以得出L0，R以及r0的关系变化，如图1所示，有限长激光脉冲要在部分离化等离子体中传播，L0，r0及R不是独立的，必须满足一定的条件才能在其中传播。由于激光在部分离化等离子体中传播时功率守恒时，a0→∞，这显然与实际不符合;取 r0≤40μm时，随着R的增大，L0取值增大，但增大幅度不明显;而取r0=100μm时，随着R的增大，L0取值会急剧地增大，此时不利于分析各参量对于激光传播过程的影响。

Fig.1 Variations of initial laser pulse length L0for different intensity of polarization nonlinearity R and initial spot size r0

为了利于各参量影响分析，令r0=40μm，进行数值求解，得到Rm=210.635时，此时激光匹配传输，进一步通过改变等离子体的电离程度可得到图2，即R值不同时激光归一化焦斑半径 r～s和脉冲宽度 L～随归一化传播距离 z～的演化关系。从图2中可知，随着部分离化等离子体电离程度的增大，部分离化等离子体中的激光自聚焦得到了有效的增强，而且随着电离程度的越高，激光自聚焦现象越明显。首先可以看出R＞Rm时激光自聚焦效应比R＜Rm时要大，当R＞Rm时，如图2中的R=220曲线所示，部分离化等离子体中的各种自聚焦效应大于激光脉冲的真空衍射效应，随着激光传播距离增大，激光焦斑半径与脉冲宽度塌缩;当R＜Rm时，如图2中的R=100曲线所示，激光的脉冲宽度与焦斑半径随传播距离增大而增大，主要表现衍射发散效应。而且在传播相同距离时，激光脉冲发散时，径向存在的等离子体通道自聚焦对 r～s的发散有抑制作用，L～值始终大于 r～s值，所以在部分离化等离子体中，有限长激光脉冲传播时引入变化的脉冲宽度值是有必要的。

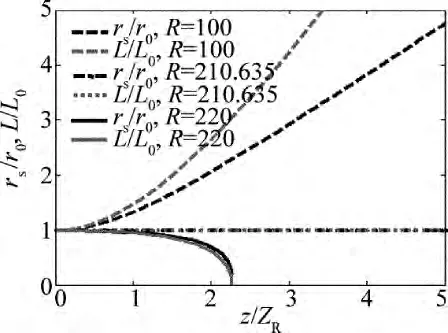
Fig.2 Variations of normalized spot size~rsand pulse length~L of a laser pulse with normalized propagating distance~z for different intensity of polarization nonlinearity R

根据演化方程组(12)式、(13)式可知，等离子体的电离程度对尾波场的各分量也有影响，给定激光脉冲强度与等离子密度时，可以得不同R值下，TWF和LWF单独作用时激光焦斑半径和脉冲宽度随传播距离 z～的演化关系，如图3所示。在R=100时，单独考虑TWF作用，激光脉冲是衍射发散，而单独考虑LWF，激光脉冲发生聚焦直至塌缩;随着R的增大，在R=220时，TWF作用的激光脉冲也产生了明显的自聚焦效应。由此可得:在相同等离子体电离程度R时，LWF对激光自聚焦效应的增大作用比TWF的增大作用要强;随着等离子体电离程度R增大，TWF与LWF对激光在部分离化等离子体中自聚焦作用增强，而且电离程度愈大增强作用愈明显。另外，在部分离化等离子体中，影响激光尾波场效应的参量还有很多，如激光脉冲初始强度a0、等离子体密度n0等，如当激光脉冲强度及等离子体电离程度一定时，随着等离子体密度n0的增大，尾波场效应增大，激光在部分离化等离子体中的自聚焦作用增强。

Fig.3 Variations of wakefield effect for different intensity of polarization nonlinearity R when the plasma density is n0=0.05

3 结论

从有限长激光脉冲在部分离化等离子体中传播的激光场与尾波场满足的耦合方程组出发，考虑了激光真空衍射、相对论自聚焦、部分离化非线性以及激光尾波场效应的影响，通过分析激光脉冲焦斑半径和脉冲宽度满足的耦合方程，详细讨论了尾波场的各分量对激光传播特性的影响。要保证有限长激光脉冲在部分离化等离子体中传播，初始激光脉冲宽度L0、初始焦斑半径r0、非线性极化强度R必须满足(14)式，并存在等离子体电离程度R=Rm时激光脉冲匹配传播;而且在部分离化等离子体中，激光脉冲发散时，L～的增长始终大于的增长，所以L～的变化对激光脉冲的传播是非常重要的;随着等离子体R值增大，激光的自聚焦效应增强，并当R＞Rm时，可以明显的观察到激光的自聚焦效应;R值相同时，TWF比LWF对激光脉冲的自聚焦作用要小，尾波场对激光自聚焦的增强作用会随着等离子电离程度增大而增强。值得说明的是，当前激光与部分离化等离子体之间的相互作用有很多新的观点提出，通过研究激光在部分离化等离子体中传播特性可以进一步理解其物理机制，为以后实验研究提供理论指导。

［1］ TAJIMA T，DAWSON J M.Laser electron accelerator［J］.Physics Review Letters，1979，43(4):267-270.

［2］ NUCKOLLS J H，WOOD L，THIESSEN A R，et al.Laser compression of matter to super-high densities:thermonuclear(CTR)Applications［J］.Nature，1972，239(15):139-142.

［3］ TABAK M，HAMMER J，GLINSKY M E，et al.Ignition and high gain with ultrapowerful lasers［J］.Physics Plasmas，1994，1(5):1626-1634.

［4］ LINDL J D，Development of the indirect-drive approach to inertial confinement fusion and the target physics basis for ignition and gain［J］.Physics Plasmas，1995，2(2):3933-4025.

［5］ ESAREY E，SPRANGLE P，KRALL J，et al.Overview of plasmabased accelerator concepts［J］.IEEE Transactiong Plasma Science，1996，24(2):252-288.

［6］ HAO D Sh.A new accelerated mechanism of protons in high power laser-plasma［J］.Laser Technology，2012，36(4):653-656(in Chinese).

［7］ SPRANGLE P，HAFIZI B，PENANO J R，et al.Wakefield generation and GeV acceleration in tapered plasma channels［J］.Physics Review，2001，E63(5):056405.

［8］ MILCHBERG H M，DURFEEⅢ C G，MCILRATH T J.High-order frequency conversion in the plasma waveguide［J］.Physics Review Letters，1995，75(13):2494-2497.

［9］ MAcKLIN J，KMETEC J，GORDON C.High-order harmonic generation using intense femtosecond pulses［J］.Physics Review Letters，1993，70(6):766-769.

［10］ ZHOU J，PEATROSS J，MURNANE M M，et al.Enhanced highharmonic generation using 25fs laser pulses［J］.Physics Review Letters，1996，76(5):752-755.

［11］ SPRANGLE P，ESAREY E.Interaction of ultrahigh laser fields with beams and plasmas［J］.Physics Fluids，1992，B4(7):2241-2248.

［12］ HONG X R，XIE B S，ZHANG S，et al.Wakefield effects and solitary waves of an intense short laser pulse propagation in a plasma channel［J］.Physics Plasmas，2011，18(10):103106.

［13］ HU Q L，XIAO G L，RUAN W，et al.One-dimensional EM solitons in ultrashort intense laser pulse-partially stripped plasmas［J］.Physics Letters，2010，A374(7):965-968.

［14］ SPRANGLE P，ESAREY E，HAFIZI B.Propagation and stability of intense laser pulses in partially stripped plasmas［J］.Physics Review，1997，E56(5):5894-5907.

［15］ SPRANGLE P，ESAREY E，HAFIZI B.Intense laser pulse propagation and stability in partially stripped plasmas［J］.Physics Review Letters，1997，79(6):1046-1049.

［16］ MANGLES S P D，MURPHY C D，NAJMUDIN Z，et al.Monoenergetic beams of relativistic electrons from intense laser-plasma interactions［J］.Nature，2004，431(7008):535-538.

［17］ GEDDES C G R，TOTH C S，van TILBORG J，et al.Observations of longitudinal and transverse self-injections in laser-plasma wakefield accelerators［J］.Nature，2004，431(7008):538-541.

［18］ FAURE J，GLIEC Y，PUKHOV A，et al.A laser-plasma accelerator producing monoenergetic electron beams［J］.Nature，2004，431(7008):541-544.

［19］ LU W，HUANG C，ZHOU M，et al.Nonlinear theory for relativistic plasma wakefields in the blowout regime［J］.Physics Review Letters，2006，96(16):165002-165005.

［20］ LEEMANS W P，NAGLER B，GONSALVES A J，et al.GeV electron beams from a centimetre-scale accelerator［J］.Nature Physics，2006，2(10):696-699.

［21］ LIU M P，ZHENG Z，LIU S Q.Effects of Relativistic and ponderomotive nonlinearities on an intense laser pulse propagation in a plasma channel［J］.Communications in Theoretical Physics，2012，58(10):569-572.

［22］ PALLAVI J，VIJAY S，AJAY K，et al.Self-focusing and compression of laser pulses in partially stripped plasma［J］.Physics Plasmas，2011，18(7):073105.