多元外辐射源单站时差定位技术*
于钦添,彭华峰,孙正波
(盲信号处理重点实验室,成都610041)
1 引 言
外辐射源定位是目前国内外关注度非常高的研究方向,其基本原理是利用广播、电视、卫星或无线通信信号等作为外部照射源构成双/多基地雷达来探测目标,具有良好的探测与抗摧毁性能[1-2]。传统多站体制下的外辐射源定位适合在陆基使用,多站的几何配置会影响到定位精度,这就给多站选址带来了困难[3]。传统的单站无源定位需要采用测向与时差结合的方式实现定位,这种方法对来波方向的测量精度有较高的要求[4]。
美国的洛克希德公司是最主要的无源雷达研发机构,该公司研发的AULOS 系统能够对常规警戒雷达接收到的信号再进行精确测量,对目标进行高精度的定位,而且分辨率要比普通警戒雷达高两个数量级。该系统也是一款新的集成化的外辐射源雷达定位系统,已经完成了其运用FM 频段的两种外辐射源雷达模型的测试并着手于基于移动平台的外辐射源雷达测试活动[5]。近20年来,国内基于数字多媒体广播、同步卫星等作为外辐射源进行目标探测以及测轨的实验系统已经建成,并逐步开展了研究[6-7]。在多站体制下,利用外辐射源对目标进行定位以及跟踪的算法也比较成熟。多站体制下定位精度受站址误差以及站址分布的影响较大,合适的站址分布以及较低的站址误差是实现高精度定位的关键之一[9-10]。
本文提出了利用多元外辐射源实现单站时差定位方法。通过对单站接收到的多个外辐射源信号进行优化选择,既可以利用敌方非合作照射源实现“长基线”布站,也可以选择卫星外辐射源与地面外辐射源结合实现空间立体布站。这相比多站体制下只能在单边地面附近布站具有很强的优势,具有很好的研究意义。文中首先推导了提出的新体制下的定位算法以及定位误差传递方程,并针对不同基线长度、时差测量精度、站址分布的情况进行仿真分析,进而对利用卫星与地面外辐射源联合的定位方式进行了仿真,验证了本文所提定位方法对定位精度的提升效果,为基于多元外辐射源单站定位系统的搭建提供了理论基础。
2 多元外辐射源单站时差定位原理
2.1 定位原理
多元外辐射源单站时差定位的原理如图1所示,单站同时接收多个外辐射源信号的直达波信号以及目标回波信号,通过优化选择3 个(或以上)最合适的外辐射源信号可以计算得到3 个时间差(或以上)。由于利用3 个时间差就可以实现对目标的三维时差定位,因此下面在推导定位算法的时候以优化选择出来的3 个外辐射源为例进行推导。

图1 多元外辐射源单站时差定位模型Fig.1 The principle of single observer TDOA location technology based on multiple external emitters
假设t 时刻目标位置为 (xt,yt,zt),接收站位置是 (xc,yc,zc),3 个辐射源的位置分别为 (x1,y1,z1)、(x2,y2,z2)、(x3,y3,z3),则目标和辐射源到接收站之间的距离分别是rtc、r1c、r2c、r3c,记辐射源到目标之间的距离为rt1、rt2、rt3,则接收站接收到二次反射与直达波信号之间的距离差分别记为Δrt1、Δrt2、Δrt3,则测量方程为

式中,c =299 792 458 m/s为电磁波在空间的传播速度。
式(1)简写为向量形式可得
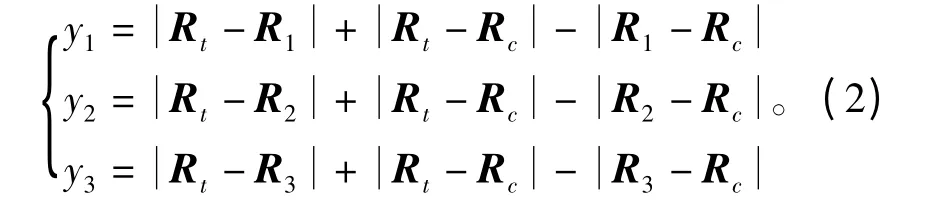
式中,y1、y2、y3分别表示3 个外辐射源直达波信号与目标回波信号经过路径的距离差,Rt表示目标的位置向量,Rc表示接收站的位置向量,R1、R2、R3分别表示3 个接收站的位置向量。
2.2 定位算法
上述方程经过变形得到

推导得到
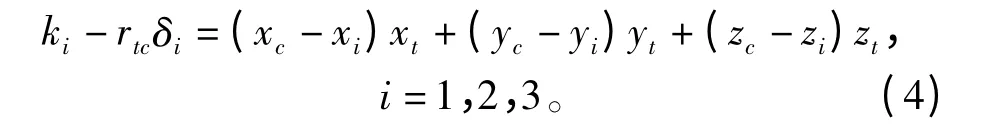
其中,
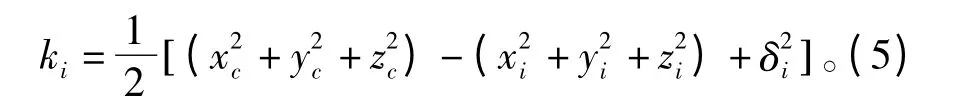
因此,由式(4)可得

假设rtc为一已知值,则可将其看成一个线性方程组,可表示为

其解的表达式为X=A-1F,其中

设

则式(6)的解可写成
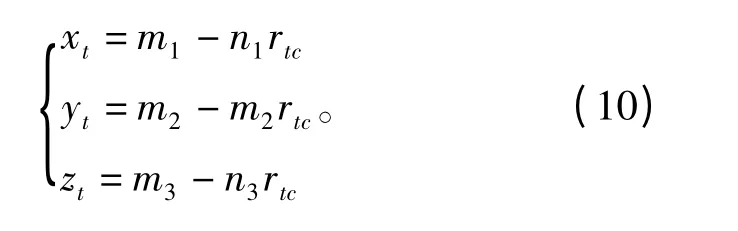
其中,

即

将式(10)代入方程组(6)中rtc等式可得
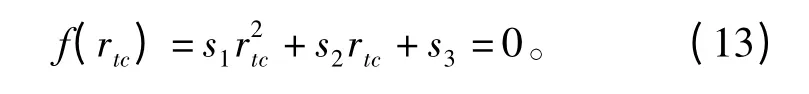
其中,

解方程(14)得到

在上面的两个解中根据先验知识取某个正值解(距离大于0),则将rtc代入式(10)得到

以上是本文提出的多元外辐射源单站时差定位算法的推导,该算法为外辐射源定位提供了新的思路,与传统的外辐射源单站定位相比,不需要进行测向,只利用时差就可以实现三维定位。相比多站定位体制,又克服了布站选址困难的问题。
2.3 算法流程
上述定位方法的算法流程如下:
第1 步:计算ric(i=1,2,3);
第2 步:构造δi=Δrt1+r1c和δ = [ δ1,δ2,δ3]T;
第3 步:计算公式(7)中的A 矩阵;
第4 步:计算A 矩阵的逆矩阵A-1;
第5 步:根据式(5)计算ki的值,K= [ k1,k2,k3]T;
第6 步:根据式(12)计算m 向量和n 向量;
第7 步:计算式(14)中的各si(i=1,2,3)分量;
第8 步:由一元二次方程(13)求解rtc;
第9 步:由式(15)解算目标位置Rt。
3 定位误差传递方程
由定位方程可得

则三站时差测量的偏导数方程为

由计算偏导数方程(17)可得

可得到向量形式:

则

变形可得

方程右边构造一个新的观测量ΔZ,其最优估计为

式中,W 为Cov (ΔZ)的对角线元素的倒数:

目标位置估计误差协方差为

式(21)即多元外辐射源信号单站时差定位的误差传递方程。
4 定位精度仿真分析
4.1 测量精度影响分析
在实际对目标进行定位的过程中,对时差的测量和估计必定会导致时差测量误差。实际操作中多普勒频移、接收机热噪声等因素会使时差测量精度下降。下面选择3 个固定的地面外辐射源,在时差测量精度不同时对定位精度进行仿真。3 个外辐射源的坐标为[124,30,0]、[125,30,0]、[126,30,0],接收站的坐标为[125,32,0],考虑到实际中地面外辐射源传播距离有限,在仿真中选择的外辐射源距离接收站不超过300 km。
图2~4分别是时差测量误差为100 ns、150 ns时的定位二维误差以及三维误差。从图中可以看出,时差测量精度越高,定位精度越高。该算法在水平方向上的定位精度很高,定位误差主要集中在高度方向上。这是由于本次仿真中采用的外辐射源都位于地面附近、高度方向上的距离相差不大导致的,可以利用卫星与地面外辐射源结合的方式提高高度方向上的定位精度。

图2 定位二维误差(时差测量误差100 ns)Fig.2 Two-dimensional location error while the precision of TDOA measurement is 100 ns
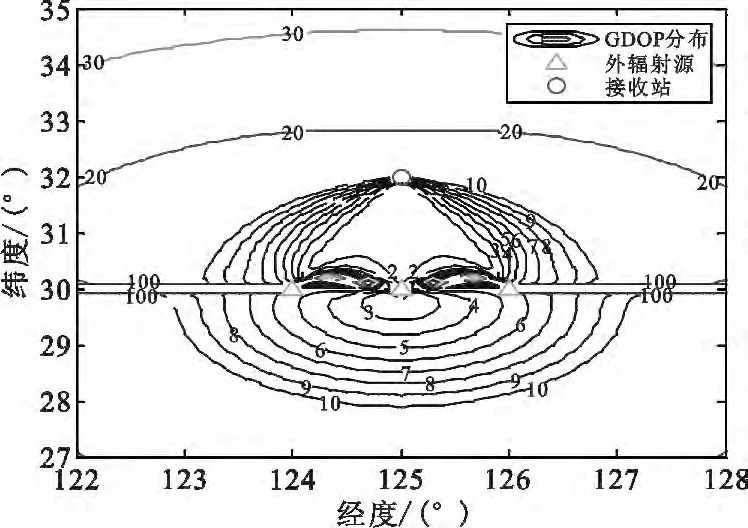
图3 定位三维误差(时差测量误差100 ns)Fig.3 Three-dimensional location error while the precision of TDOA measurement is 100 ns

图4 定位三维误差(时差测量误差150 ns)Fig.4 Three-dimensional location error while the precision of TDOA measurement is 150 ns
4.2 定位几何分布影响分析
在本文提出的基于多元外辐射源信号的时差定位算法中,所选择的外辐射源的几何分布成为影响定位精度的关键因素之一。在同样的时差测量精度和接收站位置的条件下,在仿真中按接收站和外辐射源分别构成T 型分布、四边形分布、Y 型分布,利用GDOP 方法分析各种几何分布下的定位精度。
从图5~7中可以看出,Y 型分布下,接收站的各个方向上定位精度都很高,在接收站300 km范围内,大部分区域定位误差在5 km以内,且探测范围内不存在大面积的定位盲区,最适合在实际中应用。

图5 四边形分布的GDOP 仿真结果Fig.5 The GDOP simulation result of the quadrilateral geometric distribution

图6 Y 型分布的GDOP 仿真结果Fig.6 The GDOP simulation result of the Y geometric distribution

图7 接收站坐标(125,31)时GDOP 仿真结果Fig.7 The GDOP result when the receiving observer is at(125,31)
4.3 外辐射源基线长度影响分析
在定位几何分布相同的情况下,不同的基线长度也会对定位精度产生影响。下面将在接收站和定位几何分布固定的情况下,改变基线长度,进行定位精度分析。
图7是在与图3同样的外辐射源几何分布条件下,通过拉近接收站与外辐射源的距离减小基线长度的GDOP 仿真结果,图7中接收站的坐标为[125,31,0],图3中接收站坐标为[125,32,0]。通过分析可以看出基线长度越大,接收站探测范围内的定位精度越高。在利用多元外辐射源实现单站时差定位时,可以利用敌方与我方外辐射源共同定位实现双边长基线布站,具有多站体制所不具备的优势。
4.4 Monte-Carlo 仿真验证
为了验证算法的有效性,利用Matlab 对定位算法进行了仿真。假设的目标位置[125,31,7000],接收站位置[125,32,0],外辐射源位置[124,30,0;125,30,38 000 000;126,30,0],时差测量精度100 ns。
仿真中选取的参数与实际环境类似,目标设定为飞行高度为7000 m的空中目标,利用一个同步卫星外辐射源、两个地面外辐射源实现联合探测验证算法的可行性。该定位算法同样适用于不同站址分布以及不同时差测量精度。
图8是对目标进行定位的仿真结果,仿真利用Monte-Carlo 方法进行1000次,以验证算法的有效性。从图中可以看出,1000次对目标定位的点都集中在目标点附近,验证了算法的有效性。
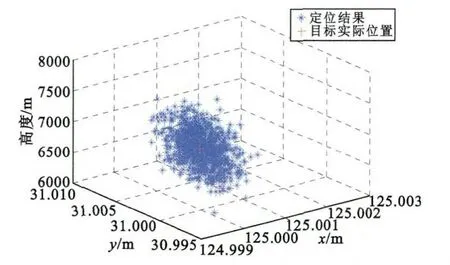
图8 目标三维定位仿真结果Fig.8 Three-dimensional location results of the target
从图9和图10可以看出,这次仿真定位三维误差集中在0~400 m之间,平均误差在200 m左右。水平方向的定位误差在15 m以内。通过图8可以看出,在同样分布的情况下,3 个外辐射源均在地面附近时,该目标的定位误差2 km以上,说明利用卫星外辐射源与地面外辐射源联合对目标进行单站时差定位,定位精度可以提高10 倍以上。

图9 目标三维定位误差Fig.9 Three-dimensional location errors of the target
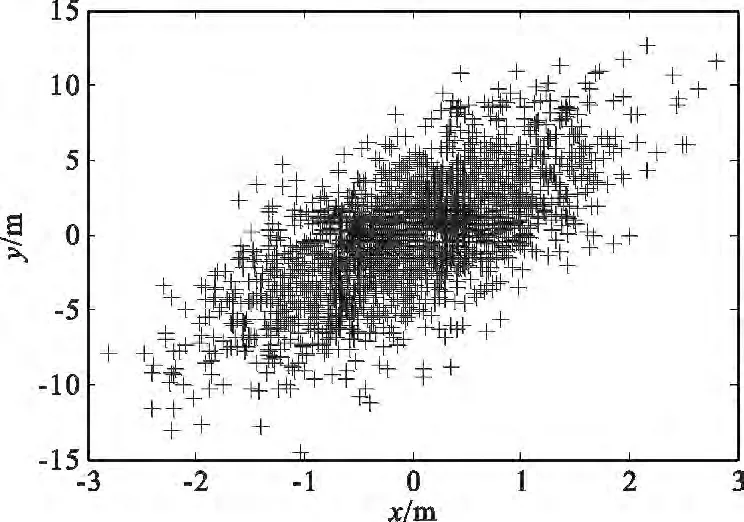
图10 目标二维定位误差Fig.10 Two-dimensional location errors of the target
5 结束语
本文提出了利用多元外辐射源实现单站时差定位的新方法,推导了定位算法和误差传递方程,通过仿真验证了该算法的有效性。仿真结果表明:利用多元外辐射源实现长基线、Y 型布站的定位精度最高,利用卫星外辐射源与地面外辐射源结合定位,三维定位精度可以提高10 倍以上。该方法有效解决了传统多站体制高度方向上定位精度差的缺点,利用单站实现了时差定位,避免了传统单站无源定位中测角误差对定位精度的影响。本文提出的定位方法为外辐射源定位的研究提供了新的思路,在理论上具有一定价值。通过接下来对多元外辐射源目标检测技术的研究,进而利用多元外辐射源实现单站时差定位,在工程上也具有很好的发展前景。
[1] Schroeder A,Edrich M,Winkler V. Multi- Illuminator Passive Radar Performance Evaluation[C]//Proceedings of 2012 13th International Radar Symposium. Warsaw:IEEE,2012:61-64.
[2] 徐世友,陈曾平. 机会照射源雷达系统中外辐射源的选择[J].现代雷达,2007,29(10):16-19.XU Shiyou,CHEN Zengping. Selecting of Illuminator in Opportunistic Illuminator Radar System[J].Modern Radar,2007,29(10):16-19.(in Chinese)
[3] 俞志强,王宏远,武文.四站时差定位布站研究[J].电子学报,2005,33(12A):2308-2311.YU Zhiqiang,WANG Hongyuan,WU Wen. 4- Station Disposition Research of Position Location Using TDOA[J]. Acta Electronica Sinica,2005,33(12A):2308-2311.(in Chinese)
[4] 李望西,黄长强,王勇,等. 一种利用相位差变化率的机载单站无源定位方法[J]. 电讯技术,2012,52(1):13-17.LI Wangxi,HUANG Changqiang,WANG Yong,et al.Airborne Signal Observer Passive Location Using Phase Difference Rate of Change[J].Telecommunication Engineering,2012,52(1):13-17.(in Chinese)
[5] Fulcoli R,Sedehi M,Tilli E.AULOS,A passive cover radar system[J].Microwave Journal,2013,56(1):72-82.
[6] 唐慧,万显荣,陈伟,等. 数字地面多媒体广播外辐射源雷达目标探测实验研究[J]. 电子与信息学报,2013,35(3):575-580.TANG Hui,WAN Xianrong,CHEN Wei,et al.Experimentation on Target Detection with Passive Radar Based on Digital Terrestrial Multimedia Broadcasting [J]. Journal of Electronics&Information Technology,2013,35(3):575-580.(in Chinese)
[7] 彭华峰,曹金坤,郑超.同步卫星无源测轨中的时差定位与精度分析[J]. 系统工程与电子技术,2012,34(11):2219-2225.PENG Huafeng,CAO Jinkun,ZHENG Chao. Positioning principles and precision analysis of passive measurement of GEO satellite’s orbit[J].Systems Engineering and Electronics,2012,34(11):2219-2225.(in Chinese)
[8] 陈玲,陈德煌. 多站无源定位系统中的机动目标跟踪算法[J].电讯技术,2010,50(11):10-14.CHEN Ling,CHEN Dehuang.Tracking Algorithm for Maneuvering Target in Multiple Passive Sensor System[J].Telecommunication Engineering,2010,50(11):10-14.(in Chinese)
[9] 黄知涛,周一宇,姜文利.基于外辐射源信号的时差定位系统定位精度分析[J]. 系统工程与电子技术,2010,32(11):2257-2262.HUANG Zhitao,ZHOU Yiyu,JIANG Wenli.Location precision analysis for passive surveillance system exploiting noncooperative transmitters[J].System Engineering and Electronics,2010,32(11):2257-2262.(in Chinese)
——2022 F1意大利大奖赛

