数据链信息连续引导雷达搜索策略*

赖作镁，乔文昇，古 博，吴必富

(中国西南电子技术研究所，成都610036)

1 引 言

在战斗机空战过程中，由于隐身作战模式或为满足其他战术需求，通常采用多传感器协同工作的方式完成目标的协同搜索与跟踪，引导搜索是最重要的多传感器协同应用方式，不仅能减少雷达辐射时间，还能提高雷达发现目标的概率［1－2］。

根据引导信息的数据特点，可以将引导搜索问题分为单拍信息引导和多拍连续信息引导两大类，单拍信息引导指引导信息仅有一拍，多拍连续信息指采用连续多拍信息进行引导。Thomas G. Haskins［3］通过定义引导成功概率对单拍信息引导情况下的传感器搜索性能进行了分析。David E.Jeffcoat 等［4］针对单拍信息引导搜索问题，对多次相互独立的搜索建立平均搜索概率，采用马尔科夫链预测法实现。模糊控制法［5］通过定义模糊逻辑对成功引导概率进行控制，实现最优决策。从国内外情况可以看出，国内外引导搜索研究目前主要在单拍信息引导方面，且引导搜索决策重点关心雷达探测性能，如我方雷达对敌方目标的发现概率，而极少关心雷达隐身性能如敌方电子支援测量(ESM)对我方雷达的截获概率，难以满足现代战斗机隐身作战需求。

本文将从多拍连续引导问题出发，综合考虑雷达探测性能以及雷达被敌方无源探测系统的截获性能。多拍连续引导信息的精度可能有高有低，数据率也可能有快有慢，如何设计可行、最优的引导策略对降低雷达被敌方截获的概率、减少雷达辐射时间非常重要，但目前没有看到国内外有相关的研究报道。本文的主要研究思路如下:基于经典的成功引导概率公式，采用概率方法分别建立多拍连续引导信息与累积发现概率、累积被检测概率之间的关系，在此基础上采用动态规划方法建立多阶段动态决策模型，满足雷达探测性能的条件下获得最优的雷达隐身性能。最后，基于典型作战场景，对模型进行仿真验证，结果表明，本文所提方法获得的最优策略相比于经验搜索策略减少雷达辐射时间67.5%，相比于模型保守策略减少雷达辐射时间83.75%。

2 引导信息与雷达探测性能及雷达隐身性能的关系

本节以数据链引导信息为例，重点研究连续多拍引导信息对雷达探测性能与雷达隐身性能的影响。

2.1 数据链引导信息对雷达探测性能的影响

针对连续多拍信息引导情况下的引导搜索问题，雷达探测性能的典型表征指标包括累积发现概率、虚警概率和发现时间，这里选择累积发现概率作为研究对象。

雷达搜索的累积发现概率可以定义为:从搜索执行开始到某时刻为止，目标至少被发现一次的概率。累积发现概率Prd与引导信息w、雷达性能参数u、雷达搜索参数等有关。雷达搜索典型参数包括搜索中心、搜索范围、搜索次数等。

累积发现概率的解析表达式可以表示为如下迭代形式:

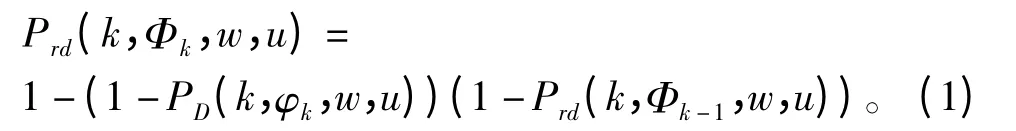
式中，φk表示k 时刻的雷达搜索活动，Φk－1=(φ1，φ2，…，φk－1)表示前k－1 个时刻的雷达搜索活动序列。PD(k，φk，w，u)表示当前k 时刻发现目标的概率，是当前时刻的传感器检测概率与累积的成功引导概率(累积到k 时刻为止，目标存在传感器扫描范围内的概率)的乘积，具体公式也可以表示为

式中，当前时刻的传感器检测概率Pg(k，φk，w)等于传感器固有检测概率Pd在搜索参数(如雷达扫描次数)上的累积:

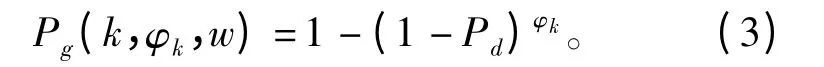
另外，累积的成功引导概率可以表示为上一时刻的成功引导概率的后验概率与目标运动转移的乘积，具体公式如下:

式中，K 表示目标运动状态转移，P+e(k－2，Φk－1，w，u)表示根据贝叶斯后验概率公式进行成功引导概率的更新。成功引导概率等于在方位、俯仰上的成功引导概率的乘积:

式中，Pea、Pee与当前时刻数据链引导的方位精度、俯仰精度有关，具体计算方法可以参见文献［6－7］。

2.2 数据链引导信息对雷达隐身性能的影响

针对连续多拍信息引导情况下的引导搜索问题，雷达隐身性能的典型表征指标包括累积被检测概率、累积被检测时间等，这里选择累积被检测概率作为研究对象。

雷达搜索的累积被检测概率可以定义为:从搜索执行开始到某时刻为止，目标至少被敌方检测一次的概率。累积被检测概率Pesm与引导信息w、雷达搜索参数、雷达性能参数u、敌方无源探测系统性能参数ψ 有关。

同理，累积被检测概率的解析表达式可以表示为如下迭代形式:

式中，PE(k，φk，w，u，ψ)表示当前k 时刻被目标检测的概率，是当前时刻敌方传感器对我方雷达的检测概率与累积的成功引导概率的乘积，具体公式也可以表示为

式中，Pe(k－1，Φk－1，w，u，ψ)的计算方法同上。当前时刻敌方传感器检测我方雷达的概率Ph(k，φk，w，ψ)是时域、频域、空域、能量域四方面概率的乘积，具体计算方法请参见文献［8］。

3 数据链引导雷达搜索优化决策模型

建立了多拍连续信息引导情况下累积发现概率、累积被检测概率的关系式以后，我们建立优化决策模型，实现满足发现概率条件下优化被检测概率，使得雷达隐身性能最优。多个时刻累积被检测概率最优的非线性规划模型表示如下:

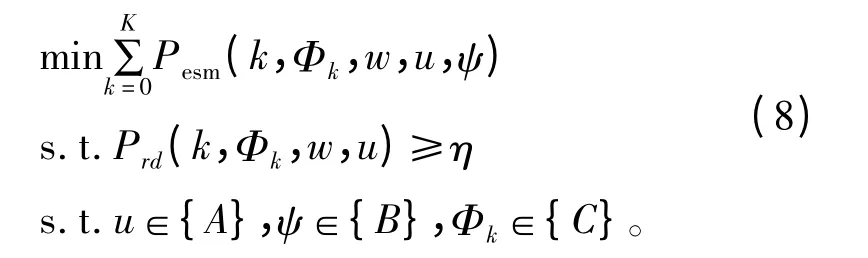
式中，集合{A}、{B}、{C}分别表示雷达性能参数、敌方无源探测系统性能参数、雷达搜索参数的值域范围或边界。

多拍连续引导搜索问题可以采用马尔科夫过程描述，故采用动态规划方法将多时间片累积最优转化为单步最优。动态规划的四元组{S，Φ，K，J}分别表示状态、决策、状态转移与收益函数。其中，状态向量为Sk= (Prd，Pesm);状态转移Kk分别参见累积发现概率和累积被检测概率的表达式;假设收益函数为动态规划所有阶段被检测概率之和:

式中，J1，K表示从1～K 阶段。

这样，非线性规划模型可以改写成

建立多阶段动态规划优化决策模型以后，可以采用经典的值迭代算法［9］完成动态规划模型的求解，获得雷达搜索的最优策略。

4 模型验证与分析

4.1 引导信息与雷达发现概率的关系仿真分析

(1)引导信息精度与雷达发现概率的关系

假设引导信息的方位误差在0.1°～2°变化，俯仰误差固定为1°，方位搜索范围取3σ 范围，俯仰扫描两线，搜索次数取2 次，雷达波束宽度为3°，仿真结果如图1所示。

图1 引导信息精度与雷达发现概率的关系曲线Fig.1 Relationship between the cue information error and the radar detection performance

从仿真结果可以看出，雷达发现概率随着引导信息误差的增大而减小，但当引导信息精度小于1°时，由于此时单个雷达波束宽度就可以对搜索范围进行单点覆盖，所以雷达发现概率几乎相同。

(2)引导信息时延与雷达发现概率的关系

假设引导时延在0.1～5 s 变化，方位搜索范围取3σ 范围，俯仰扫描两线，搜索次数取2 次，仿真结果如图2所示。

图2 引导信息时延与雷达发现概率的关系曲线Fig.2 Relationship between the cue information time delay and the radar detection performance

从仿真结果可以看出，雷达发现概率随着引导信息时间延迟的增大而减小。

4.2 模型建模及求解仿真验证

假设二对一作战场景，我方两架飞机之间通过数据链通信，其中一架飞机将目标信息通过数据链引导一架飞机进行目标搜索，具体的连续多拍数据链信息如表1所示。

按照本文所提出的方法建立多阶段动态规划优化决策模型，这里取阶段数N=5。假定雷达搜索波束宽度为3°，也即雷达搜索的最小范围为3°，雷达搜索的最大范围取最大引导误差的6 倍即12°。同理，根据雷达的极限扫描速度，假定雷达搜索次数最多4 次，这样每个阶段可能的搜索策略共有16 种，5个阶段的搜索策略共有165=1 048 576种。期望获得的优化目标为:满足发现概率大于0.92 情况下使得被检测概率最小。模型解算获得的最优策略及其对应的性能如表2所示。

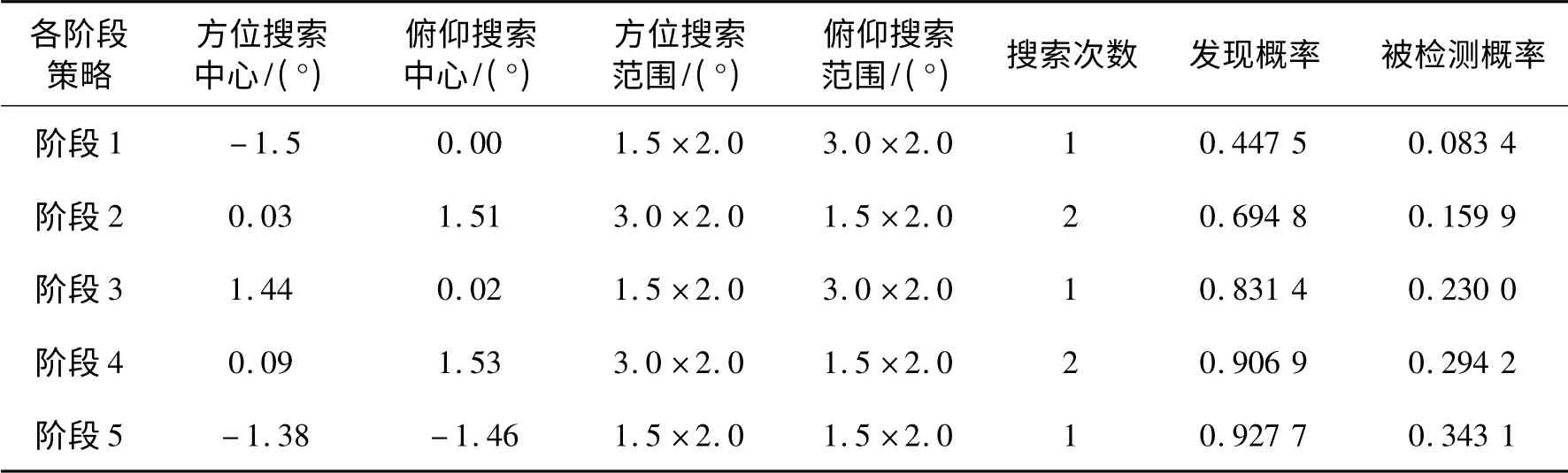
表2 最优策略及其对应的探测性能和隐身性能Table 2 Detection and stealthy performance of optimal search strategy

同时，可以从诸多策略中寻找出模型保守策略，即搜索范围、搜索次数等决策参数取极限边界时的搜索策略。表3中的典型搜索策略假定采用3σ 原则确定方位搜索范围，俯仰扫描两线，搜索次数取2 次。

表3 三种典型策略下的雷达辐射时间对比Table 3 Comparision of radar radiation time among three typical search strategies

从表3可以看出，通过本方法获得的最优搜索策略相比于经验搜索策略能够减少雷达辐射时间67.5%，相比于模型保守搜索策略能够减少雷达辐射时间83.75%，证明本文所提方法可行、有效。

5 结束语

本文在深入分析总结单拍信息引导雷达搜索问题的基础上，对单拍信息引导搜索问题进行扩展，并以数据链信息引导为例，提出了连续多拍数据链信息引导雷达搜索的模型及最优求解策略，大大减少了我方雷达的辐射时间。本文的主要结论和贡献如下:

(1)建立了多拍连续引导信息与雷达发现概率、雷达被检测概率之间的关系，为引导搜索性能分析与模型建模奠定了基础;

(2)建立了多阶段动态规划优化决策模型，能够获得满足雷达探测性能条件下的最优隐身性能，相比于经验搜索策略，能够大大减少雷达辐射时间。

本文的方法容易扩展至其他信息的多拍连续引导。另外，今后的研究将结合射频隐身约束、射频兼容约束及雷达资源消耗等约束，考虑更全面的雷达探测性能指标如虚警概率、雷达隐身性能指标如被跟踪定位精度，对决策模型进行完善优化。

［1］ 陈国海.先进战机多功能相控阵系统综合射频隐身技术［J］.现代雷达，2007，29(12):1－4.CHEN Guohai.General RF Stealth of Airborne Multifunctional Phased Array Systems［J］.Modem Radar，2007，29(12):1－4.(in Chinese)

［2］ Hayvaci H T，De Maio A，Erricolo D. Improved detection probability of a radar target in the presence of multipath with prior knowledge of the environment［J］. IET Radar，Sonar ＆ Navigation，2013，7(1):36－46.

［3］ Haskins T G. Sensor cueing performance analysis［J］.Proceedings of IEEE，1984:262－265.

［4］ Jeffcoat D E，Krokhmd P A，Zhupanska O I. Effects of cueing in cooperative search［J］. Naval Kesearch Logistics，2006:53(8):814－821.

［5］ Nagy P G，Bier S G.Intelligent interneted sensor management systems for tactical air－craft［C］// Proceedings of the IEEE 1990 National Aerospace and Electronics Conference.Dayton，OH:IEEE，1990:321－327.

［6］ 王国宏，毛士艺.ESM 对2D 雷达引导性能分析［J］.航空学报，2002，23(4):298－301.WANG Guohong，MAO Shiyi.Performance Analysis of an ESM Guiding a 2D Radar［J］.Acta Aeronautca et Astronautica Sinica，2002，23(4):298－301.(in Chinese)

［7］ 王国宏，何友，毛士艺.IRST 对3D 雷达引导性能分析［J］.电子学报，2002，30(12):1737－1740.WANG Guohong，HE You，MAO Shiyi.Performance Analysis of Using an IRST Sensor Cueing a 3D Radar［J］.Acta Electronica Sinica，2002，30 (12):1737－ 1740.(in Chinese)

［8］ Lu Jianbin，Hu Weidong，Yu Wenxian.Phased array radar cued search strategy based on information gain［J］.Journal of System Engineering and Electronics，2008，19(2):292－297.

［9］ 姜启源.数学模型［M］.4 版.北京:高等教育出版社，2011.JIANG Qiyuan. Mathematic Modeling［M］. 4th ed. Beijing:High Education Press，2011.(in Chinese)