基于二阶矩的雷达信号盲分离*

李 飞，李国林，尹洪伟

(海军航空工程学院 七系，山东 烟台264001)

1 引 言

雷达数据处理器和雷达信号处理器是现代雷达系统中的两大重要组成部分。雷达接收到的信号首先要在信号处理器中进行处理，从而达到抑制杂波、干扰信号和检测目标信号的目的［1］。在现代电子战环境下，一般认为全频段电子战接收机每秒将面临30～100 万个脉冲流［2］。如何在日益复杂的电磁战场环境中识别有用的雷达信号是雷达信号处理领域所面临的棘手问题。此时，盲信号处理(Blind Signal Processing，BSP)技术是极佳的选择。

盲信号处理是目前信号处理中最热门的新兴技术之一［3］。盲源分离(Blind Source Separation，BSS)作为盲信号处理领域的一个重要分支，其特点是在传输信道特性和源信号分布未知的情况下，仅从传感器阵列或转换器输出的观测信号中恢复源信号的波形。盲源分离技术已被广泛地应用于雷达、通信、生物医学等领域［4－6］。

本文针对雷达接收机接收到的多路混合信号，参考Choi 所提出的基于非平稳信号去相关算法［7］，提出了一种新的构造协方差矩阵的方法，减少了噪声影响。由于新构造的协方差矩阵为正定对称矩阵，利用Hadamard 不等式提出的代价函数实现协方差矩阵联合对角化，从而完成信号分离的目的。最后通过仿真实验证明了本算法的有效性。

2 盲源分离数学模型

典型的盲源分离模型如图1所示［3］。

图1 盲源分离基本框图Fig.1 Basic block diagram of blind source separation

图中，S(t)=［s1(t)，s2(t)，…，sn(t)］T是n 维源信号，H 是m×n 阶混合矩阵，v(t)是加性噪声，在盲分离问题中这些参数认为是未知的;X(t)=［x1(t)，x2(t)，…，xm(t)］T是m 维接收信号，Y(t)=［y1(t)，y2(t)，…，yn(t)］T为分离信号，W 是n×m 阶分离矩阵，即

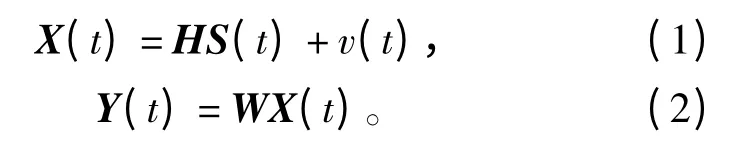
将式(1)代入式(2)得。

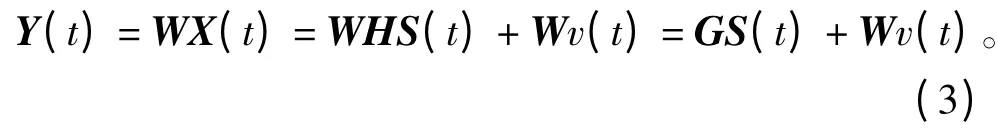
式中，G 为全局变换矩阵。在盲分离中，全局变换矩阵G 可表示为

式中，P 为排列矩阵，即每一列只有一个非零元素;D 为对角矩阵。正是由于全局变换矩阵的这种形式，导致分离信号排序和幅度的不确定性。另外，需要说明的是，根据算法的不同，在盲源分离问题中，要求源信号是相互独立或不相关的，在利用基于高阶累积量或信息论的盲分离方法中，还要求源信号中高斯分布的源信号不多于一个。

3 算法描述

本算法研究的是适定情况下的盲源分离问题，即接收信号的数目与源信号的数目相等。

3.1 数据预处理

在盲分离前，通常对接收信号进行时间、空间或空－时解相关等相应的预处理，以此改善系统的收敛特性，并消除冗余或减少噪声［3］。

首先将接收信号零均值化，即

式中，xi(t)为接收信号中第i 路信号，N 为采样点数。

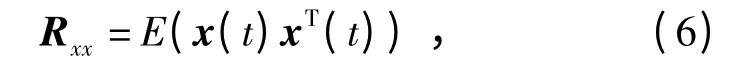
对比式(1)所描述的接收信号模型，若不能准确知道噪声的协方差矩阵，则在信噪比不高的情况下，将会严重影响分离结果。基于以上原因，采用如下方法重新构造接收信号协方差:

式中，＜·＞为平均算子，计算方式与求均值相同。此时协方差矩阵Rx(p)为对称矩阵，p 代表延时，根据不同的延时pk，由式(6)可得k 阶接收信号协方差矩阵组为

对式(8)中的元素进行特征值分解(EVD):

因为是适定盲分离问题，保证了Σ 中包含了n个特征值，U 包含了n 个特征矢量。设Σ 中各元素绝对值最大为为使协方差矩阵组R 为正定矩阵，取正实数ξ，使得将式(8)协方差矩阵组中的元素按下式进行计算更新:

式中，I 为单位矩阵。重新按式(8)计算协方差矩阵组的特征值分解，得特征值矩阵为Σ1，特征向量矩阵为U1。对接收信号x(t)进行球化:

3.2 算法推导

在对接收信号进行预处理之后，选取一组时间延时(p1，p2，…，pl)估计式(11)的协方差矩阵，可得协方差矩阵集合中元素如下式:

由式(2)，得到分离信号的协方差矩阵为

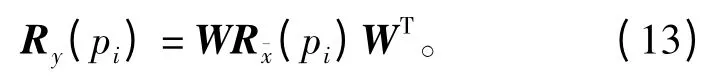
因为源信号是不相关的，故其协方差矩阵是对角阵，对角元素为各分量的自相关函数，因此，对混合信号的盲分离问题转化为式(13)的联合对角化问题。由Hadamard 不等式，可得如下目标函数［8］:

式中，D(pi)为协方差矩阵Ry(pi)的对角线元素，式(14)其梯度为

因此，

而Ryx(pi)=Ryy(pi)W－T，代入式(17)得

再考虑式(15)右侧第二部分，有

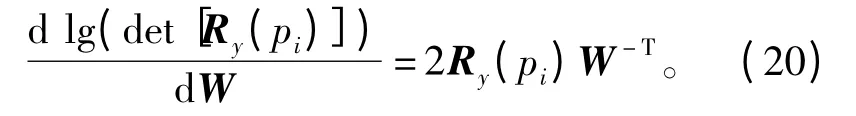
将式(18)、式(20)代入式(15)得代价函数梯度为

由牛顿迭代公式，得到分离矩阵更新公式为

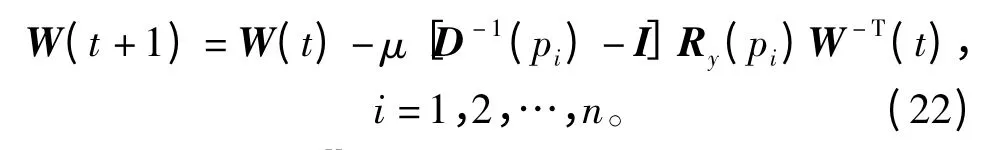
Amari 等人［9］已经证明，参数W 在一个Riemannian 空间真实最速下降方向不是而是这也被称为自然梯度，而且Amari 等人也证明采用自然梯度方法会使全局矩阵G 的收敛性能与混合矩阵H 无关。式(20)右端乘以WTW得到基于自然梯度的分离矩阵更新公式为

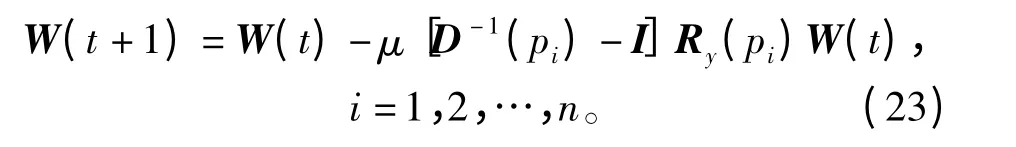
式中，μ 为更新因子。对比式(20)和式(21)可知，采用自然梯度算法，分离矩阵在更新时不必每次计算矩阵逆，因此算法性能也大大提升。在算法收敛后，根据式(2)可得到最终的分离结果。

3.3 算法步骤

本文算法具体步骤如下:

Step 1:根据式(5)对接收信号进行去均值处理，式(7)估计接收信号协方差矩阵，取不同延时pi构成协方差矩阵组;

Step 2:根据式(9)对Step 1 估计的协方差矩阵进行特征值分解，根据式(10)对协方差矩阵进行正定化处理，根据式(11)对协方差矩阵进行白化处理;

Step 3:根据式(14)计算白化后协方差矩阵组具体代价函数形式;

Step 4:根据式(16)～(22)计算代价函数自然梯度，直至算法收敛，计算过程中以WTW 替代W－T，避免迭代过程中的求逆运算;

Step 5:由式(23)估计出分离矩阵最终形式，根据式(2)计算最终分离信号。

4 仿真实验与性能分析

本文采用5 路源信号，其中感兴趣的是第3 路线性调频信号，其余信号是接收机接收到的杂波、干扰等无关信号，源信号如图2所示。

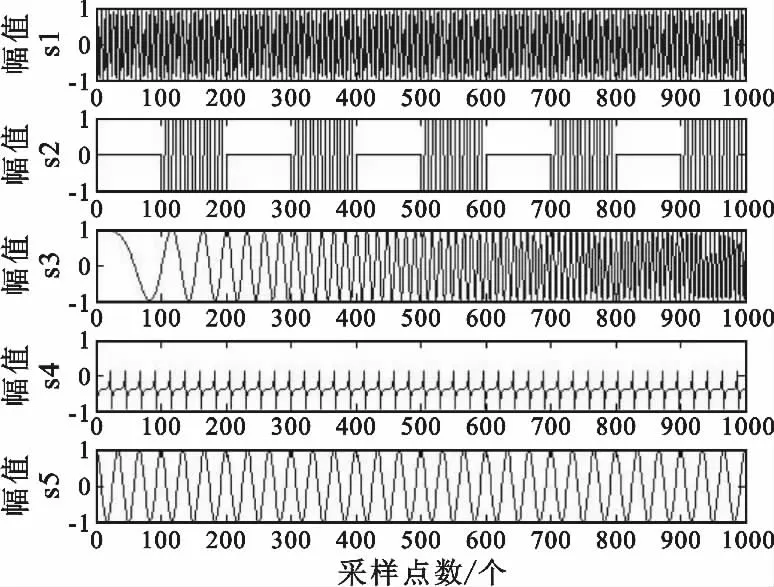
图2 源信号Fig.2 Source signals

图3是经过快速傅里叶变换(FFT)后源信号的频谱结构，可见，各信号频谱在频域是相互混叠的，区分是困难的。

图3 源信号频谱Fig.3 Frequency spectrum of source signals

混合矩阵是随机生成的5 阶满秩矩阵，在信噪比为－10 dB条件下，经过线性混合后，接收机接收到的信号形式如图4所示。

分离矩阵初值随机生成，取μ =0.001，利用式(23)进行迭代直至算法收敛，得到最终解分离信号如图5所示。

图5 本文算法分离信号Fig.5 Separated signals of the proposed algorithm

取相同参数，利用FastICA 算法最终分离结果如图6所示。

图6 FastICA 算法分离结果Fig.6 Separated result of FastICA algorithm

对比图2和图5可见，分离效果是令人满意的，尽管信号的顺序和幅度均有一定变化，但这并不影响对信号的辨识，同时也印证了盲分离问题中的两个不确定性。从图6可以看出，FastICA 算法虽然完成信号分离，但分离结果受噪声影响较大，信号时域波形毛刺较多，对比图5，证明在噪声环境中，本文算法优于FastICA 算法。

算法PI 值计算公式如式(24)所示［3］:

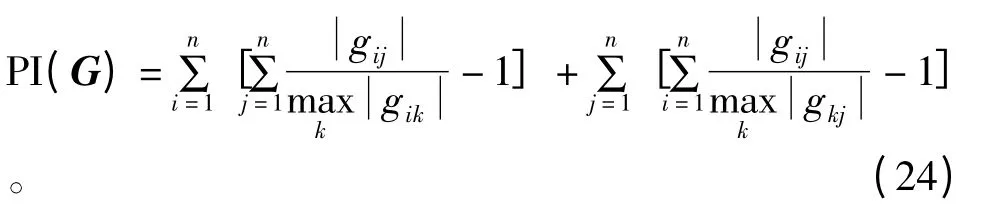
式中，G 为式(3)中的全局矩阵，gij为矩阵G 第i 行、第j 列元素。算法PI 值越小，说明其分离信号与源信号越接近。本文算法与FastICA 算法PI 值曲线如图7所示。

图7 算法PI 值曲线Fig.6 PI curves of algorithms

从图7中可以看出，在算法迭代12 次时，本文算法已经稳定收敛，而FastICA 算法收敛速度相对较慢，且PI 值明显高于本文算法，在证明分离信号精度方面，本文算法明显高于FastICA 算法。

5 结束语

要进行信号识别首先需要对接收到的混合信号进行分离。面对日益复杂的现代电磁战场，针对雷达接收机接收到的混叠信号，本文提出了一种基于盲源分离的方法。对于加性噪声的影响，构造了一组新的协方差矩阵，使其不会影响分离结果。在协方差矩阵对角化过程中，采用自然梯度的方法，避免分离矩阵更新过程中的求逆问题，提高了算法的实时性。仿真证明了相对于FastICA 算法，本文算法在噪声环境下具有更好的分离性能，为进一步的信号识别提供了可靠依据。

［1］ 何友，修建娟，张晶炜，等.雷达数据处理及应用［M］.北京:电子工业出版社，2006.HE You，XIU Jianjuan，ZHANG Jingwei，et al.Radar data processing with application ［M］ . Beijing:Publishing House of Electronics Industry，2006.(in Chinese)

［2］ 张嵘.宽带高灵敏度数字接收机［D］.成都:电子科技大学，2002.ZHANG Rong.Broadband high－sensitivity digital receiver［D］. Chengdu:University of Electronic Science and Technology of China，2002.(in Chinese)

［3］ Cichocki A，Amari S. 自适应盲信号与图像处理［M］.吴正国，译.北京:电子工业出版社，2005.Cichocki A，Amari S.Adaptive blind signal and image processing［M］.Translated by WU Zhengguo. Beijing:Publishing House of Electronics Industry，2005.(in Chinese)

［4］ Aissa－El－Bey A，Linh－Trung N，Abed－Meraim K，et al. Underdetermined blind separation of nondiajoint sources in the time－frequency domain［J］.IEEE Transactions on Signal Processing，2007，55(3):897－907.

［5］ He J A，Liu L Z.Single－channel blind source separation based on cyclic spectrum setimation［C］//Proceedings of 2013 6th IEEE International Congress on Image and Signal Processing.Hangzhou:IEEE，2013:1525－1529.

［6］ Chien J T，Hsieh H L. Convex Divergence ICA for Blind Source Separation ［J］. IEEE Transactions on Audio，Speech，and Language Processing，2012，20(1):290－301.

［7］ Choi S，Cichocki A，Amari S. Equivariant nonstationary source separation［J］. Neural Networks，2002，15(2):121－130.

［8］ Wang F S，Zhang L R，Li R，et al.Multidimensional independent subspace analysis by natural gradient［J］. Przeglad Elektrotchniczny，2012，88(9):51－54.

［9］ Amari S，Cichocki A，Yang H H. Chapter Blind Signal Separation and Extraction－Neural and Information Theoretic Approaches［M］//Unsupervised Adaptive Filtering.New York:John Wiley，1999.