由m序列构造的同级类m序列及性能研究

方俊初，张爱雪，吕 虹

(1.安徽工程大学电气工程学院，安徽芜湖2410002;2.安徽建筑大学电子与信息学院，安徽 合肥230022)

m序列用途广泛，子序列是由m序列衍生出的一种序列［1－3］。子序列很多［4－5］，对这部分子序列研究的难点在于当级数变化时，交换同样的共轭状态对的后继状态，还能否得到子序列。目前只能根据共轭状态对的特点用不同方法予以证明，文献［3］中指出符合条件的一对共轭状态并用直观的方法予以证明，文献［6］中用“模3取余法”证明了一些符合条件的共轭状态对。本文研究的是实践中发现的另一对符合条件的共轭状态对，根据其状态的构成特点，将移位寄存器的状态和反馈按奇数位和偶数位分开，分别研究它们对反馈值的影响，并选取级数不同的几个子序列，对它们的伪随机特性进行了研究，为它们的应用奠定了基础。

1 一种类m序列(子序列)的实现

经观察，在n变化的过程中，状态1010…101，其共轭状态与0101…010，及其共轭状态在状态图上始终处于交错状态，也就是满足生成子序列的条件，下面从理论上予以证明。

1.1 m序列移位寄存器抽头位置的表示方法

生成m序列的线性移位寄存器如图1所示(下面简称m序列移位寄存器)，它是由n位移位寄存器、若干个模2加法器组成的线性反馈网络及时钟发生电路构成。模2加法器的输入通过系数与移位寄存器的各位状态相联，ci=1表示此线接通，该位状态参与反馈运算;ci=0则表示该位断开，不参与反馈运算［1］。常将形成m序列时参与反馈的抽头位置用一个集合表示，如表1所示。

表1 级数n=5、6时的反馈位置Tab.1 Feedback for stage n=5 and n=6 register

表中［2，5］即表示对应的本原多项式为f(x)=1+x2+x5，也就是图 1 中c2=c5=1，c1=c3=c4=0。为下面描述方便，将每一个这样的集合统称为X。

根据m序列的特点可以用反证法来证明这个结论，若反馈抽头个数为奇数，则当移位寄存器进入全“1”状态即“111……11”时，其反馈信号必然为“1”，其下一个状态仍然是“111……11”，进入死循环，不能产生m序列。因而m序列移位寄存器的抽头个数一定为偶数，不可能是奇数。

1.2 状态转换过程的证明

定理1:状态1010…101，其共轭状态与0101…010，及其共轭状态在“圈”内必然呈交错状态，具体地说是，级数n为奇数时，一对共轭状态1010…101、1010…100和另一对共轭状态0101…010、0101…011必然成交叉状态;级数n为偶数时一对共轭状态1010…10、1010…11和另一对共轭状态0101…01、0101…00必然形成交叉状态，要证明上面的结论，需要从下面四个方面证明状态的转换过程:

(1)在n=2k+1(k=1、2……)的情况下，若X中有奇数个奇数位，则必然有这样状态转换过程:1010…100→0101…010→1010…101……

证明:在n=2k+1(k=1、2……)的情况下，若X中有奇数个奇数，根据引理1，其中必然有奇数(也可能为零)个偶数。也就是反馈线是由奇数个奇数位和奇数(也可能为零)个偶数位组成的。状态“1010…100”最高位是奇数位且为“0”其余皆为“1”，最高位是必然参与反馈的，则剩下的偶数个奇数位全为“1”，“模2加”后结果为“0”，因为偶位全为“0”，不管有几位参与反馈，结果都是“0”，总之，状态“1010…100”对应的反馈是“0”，从而进入下一个状态“0101…010”，此时奇数位皆为“0”，偶数位皆为“1”，其中奇数个偶数位参与反馈得反馈值为“1”，移位寄存器进入下一状态“1010…101”。

(2)在n=2k+1(k=1、2……)的情况下，若X中有偶数个奇数位，则必然有这样的状态转换过程:0101…011→1010…101→0101…010……

证明:在n=2k+1(k=1、2……)的情况下，若X中有偶数个奇数位，则必然有偶数个偶数位，状态“0101…011”的偶数位皆为“1”，参与反馈的偶数个偶数位“模2加”后结果为“0”，奇数位中最高位“1”必然参与反馈而其它奇数位全为“0”，即可得状态“0101…011”对应的反馈值为“1”，进入下一状态“1010…101”，此时偶数位全为“0”，“模2加”后结果为“0”，奇数位全为“1”，其中的偶数个参与反馈(必然包括最高位)，决定了反馈值为“0”，进入下状态“0101…010”。

(3)在n=2k(k=1、2……)的情况下，若X中有奇数个偶数位，则必然有这样状态转换过程:1010…11→0101…01→1010…10……

沉水植物是水体生态系统的主要初级生产者之一[5]，不仅自身具有氮、磷吸收能力，也是水体生物多样性赖以维持的基础，具有维护整个湖泊生态系统结构与功能的能力，因此恢复和构建沉水植被群落是水体富营养化治理的重要措施[6]。但沉水植被短时间内成功恢复或者重建是比较困难的，受水位波动大、截污不彻底、水体透明度低等因素制约较多，因此人工快速大面积恢复的难度较大[7-9]。笔者选取湖州仙山湖北湖和南湖入库河流近岸水域，采用不同种植方式对4种沉水植物的存活率及生长情况进行研究，旨在探索出不同沉水植物在不同环境特征下的种植技术，为沉水植物群落的恢复或重建提供技术支撑。

证明:在n=2k(k=1、2……)的情况下，若X中有奇数个偶数位，也必然有奇数(也可能为零)个奇数位。状态“1010…11”中奇数位全为“1”，即奇数位的反馈值为“1”，偶数位中只最高位是“1”，其他均为“0”，注意到最高位必然参与反馈，因而偶数位的反馈值也为“1”，这样，状态“1010…11”对应的反馈值就是“0”，移位寄存器进入下一状态“0101…01”，这时的奇数位全为“0”，偶数位全为“1”，其中奇数个偶数位参与反馈决定了反馈值为“1”，移位寄存器进入下状态“1010…10”。

(4)在n=2k(k=1、2……)的情况下，若X中有偶数个偶数位，则必然有这样状态转换过程:0101…00→1010…10→0101…01……

证明:在n=2k(k=1、2……)的情况下，若X中有偶数个偶数位，也必然有偶数(也可能为零)个奇数位。状态“0101…00”中奇数位全为“0”，即奇数位的反馈值为“0”，偶数位中除最高位外全为“1”，最高位必然参与反馈，这样偶数个偶数位形成的反馈值为“1”，因而状态“0101…00”所对应的反馈就是“1”，移位寄存器进入下一状态“1010…10”，此时，偶数位全为“0”，即偶数个偶数位形成的反馈分量是“0”，而奇数位全为“1”，其中的偶数个奇数位参与反馈，形成的反馈分量是“0”，因而状态“1010…10”对应的反馈值是“0”，进入下一状态“0101…01”。

1.3 反馈函数的提取及生成的非线性序列

这类子序列的优点是级数不同时，其反馈函数有统一的实现方法。

实现子序列，就要改变原有m序列移位寄存器的反馈函数，方法是在原有f(x)基础上附加一个函数g(x)，形成新的反馈函数f'(x)，形式如下

f'(x)=f(x)⊕g(x) (1)

其中g(x)只有在指定的共轭状态时取值“1”，否则为“0”，从而改变了f(x)在此状态处对应的反馈值，也就改变了状态转移顺序。

例如，阶数n=6时，取原本多项式1+x+x6，即反馈函数是f(x)=x1⊕x6，得到的m序列为:

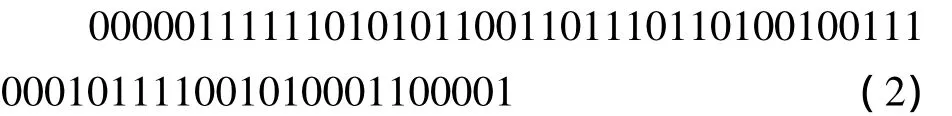
子序列的反馈函数是f'(x)=f(x)⊕，得到的新的序列(子序列)为:

2 子序列与原序列的特性比较

2.1 周期性及结构特点

子序列是在m序列移位寄存器的基础上，只改变某些状态的转换顺序，没有增加和减少原有状态，所以子序列和原m序列具有相同的码元结构。例如上述序列原序列(2)和子序列(3)，具有相同的周期63，其中“1”的个数都为32，“0”的个数都为31。

2.2 游程特性

将序列(2)和序列(3)按游程分段，结果如下:

它们的游程分布情况见表2。

从表中可见，子序列和原序列具有相同的游程结构，即n阶m序列一个周期中共有游程2n－1个，其中长度为1的游程占，长度为2的占长度为3的占，长度为n及n－1的游程特殊，都只有一个［7－8］。

2.3 自相关特性

对于一周期为p的二元序列，其自相关特性定义为:

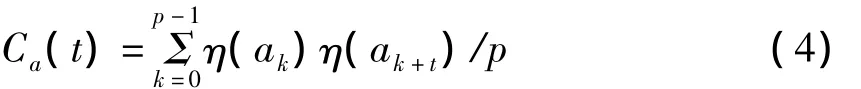
其中η(*)表示映射

Matlab环境下，对m序列和其子序列的自相关特性进行测试。

表2 游程分布情况统计Tab.2 Statistic for the run length

由图2可见，(1)m序列是线性序列，其自相关特性具有典型的二值特性。子序列是非线性序列，其自相关特性不同于m序列，呈现多值特性;(2)子序列也具有非常尖锐的自相关特性，图中可见其主峰值为1，副峰值随阶数n增大而明显减小;(3)进一步实验表明，当级数增大一定程度时，子序列的自相关特性十分接近于m序列的自相关特性［9］。

3 总结

基于本文给出的这一共轭状态对一定能获得相应的子序列，特性测试表明，这一类子序列是良好的伪随机序列。不足之处在于对子序列的自相关特性尚不能给出准确的数学表达式，只能通过测试的方法得出其趋势。

［1］肖国镇，梁传甲，王育民.伪随机序列及其应用［M］.北京:国防工业出版社，1985.

［2］尹晓琪.伪随机序列及其在通信加密中的应用［J］.现代电子技术，2005(19):42－44.

［3］吕虹，段颖妮，管必聪，等.第一类 m子序列的构造［J］.电子学报，2007，35(10):2029 －2032.

［4］方俊初，吕虹，张爱雪.产生m子序列的一种实用算法［J］.河北工程大学学报:自然科学版，2012，29(4):79－83.

［5］方俊初，吕虹.由m序列生成非线性序列的C语言实现［J］.河南科技大学学报:自然科学版，2013，34(6):47－50.

［6］吕虹，张爱雪，方俊初，等.基于母函数的非线性反馈函数及其子序列研究［J］.电子学报，2012，40(10):2128－2132.

［7］GAO ZHIHAN，FU FANGWEI.The minimal polynomial of a sequence obtained from the componentwise linear transformation of a linear recurring sequence［J］.Theoretical Computer Science，2010(411):3883 －3893.

［8］LVHONG.Design and Implementation of A Maximal Length Nonlinear Pseudorandom Sequence［C］//Proceedings of the 2009 International Conference on Computer and Commun－ications Security.2009:64 －67.

［9］GUANG GONG.Cryptographic properties of the welch －gong trans － formation sequence generators［J］.IEEE Transactionson Information Theory，2002，48(11):2837－2846.