考虑温度效应的大底盘双塔结构地震反应分析

苏 瑜，宋琛琛，于明博

(1.同济大学结构工程与防灾研究所，上海200092;2.中建三局集团有限公司建筑设计院，湖北 武汉430016)

大底盘双塔结构是近年来民用建筑中广泛应用的一种结构形式，它是由两个独立的塔楼通过底部大面积裙楼连接而成，结构的抗震性能有其自身的特殊性和复杂性［1－3］。随着近年来全球气候出现异常，季节温差两极化明显，温度作用对于建筑物造成的影响也日趋重要。然而，在实际工程中，越来越多的此类大规模建筑屡屡超过规范［4］对结构温度伸缩缝最大间距的规定。为了掌握温度应力的分布和发展规律，国内外学者对混凝土温度场计算模型的建立和求解、温度应力的计算等方面做了大量的研究［5－12］。对温度应力的计算，大多应用在工业建筑，大型公建以及市政工程方面，民建领域的应用相对较少，且以上研究大多是针对温度作用单工况展开的，有关温度作用与其它荷载组合，特别是与地震作用组合方面的研究较少［13］。2012 版荷载规范［14］虽将温度作用列入了可变荷载之列，但对于混凝土结构开裂以及徐变等因素引起的结构刚度降低而产生的温度折减的取值，设计人员具备一定的权限，针对此问题，本文对某大底盘双塔结构的温差取值进行了简化计算，并进行了温度与地震共同作用下的反应谱分析，定量地分析了温度作用对大底盘双塔高层结构的内力分布和抗震性能的影响。

1 工程概况

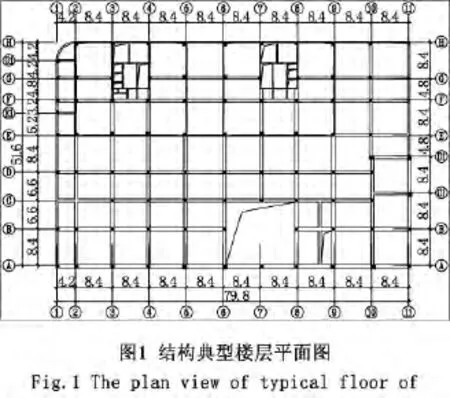
本工程位于陕西省西安市。该楼由框架结构大底盘裙房连接两个框架－剪力墙高层住宅楼，地上结构25层(含裙楼)，地下1层，1～4层为大底盘裙楼。房屋总高度为80.77 m，地下室层高3.9 m;裙楼层高由下至上分别为 5.8、4.5、4.5、3 m，塔楼层高均为3 m。出于建筑考虑和承载力以及底盘刚度的要求，本工程大底盘框架层采用6.6 ～8.4 m 跨宽扁梁框架，框架柱距为 8.4 m，底盘尺寸为 79.8 m×51.6 m。地下室顶板厚400 mm，底盘楼层板厚 180 mm，底盘顶板厚200 mm，上部塔楼楼板厚100 mm，结构所有剪力墙厚度均为250 mm。结构典型楼层平面图如图1所示。抗震设防烈度为7度(0.15 g)。场地土类别为Ⅱ类(场地特征周期Tg=0.35 s)。设计使用年限为50年。

2 模型建立

本文采用有限元分析软件SAP2000，对该结构进行抗震计算分析。简化模型为带弹簧串并联钢片系层模型，双塔楼模型如图2所示。具体过程及处理方法如下:(1)底盘裙楼楼板、屋面板(地下室和1～4层)和剪力墙均采用薄壳单元模拟采用壳单元输入模型，可同时考虑楼板平面内(平板)及平面外(弯曲)刚度，楼板尚需根据柱、剪力墙的支撑情况进行网格划分;(2)上部塔楼(5～25层)楼板采用膜单元模拟;(3)梁、柱使用杆系框架单元模拟。

3 温度作用的考虑

众多分析表明，季节温差是一种普遍存在、均匀分布在整个结构上且对结构影响较大的一种温差场。此外，由于混凝土收缩会产生类似于温度应力的作用，故本文在考虑温差的同时，将混凝土的徐变收缩折算成当量的温差作用在结构上。另外，考虑到混凝土徐变、塑性性质及裂缝等因素的影响，对温度应力进行适当折减。

(1)季节温差的确定

依据王铁梦提出的季节温差的计算公式，如下:

(2)混凝土收缩当量温差

通常将混凝土收缩对温度效应的影响考虑为混凝土收缩当量温差，由混凝土收缩量值和线膨胀系数的概念可以求得当量温差，如下式所示:

式中，εy(t)—t(以d为单位)时间的收缩;a—混凝土线膨胀系数。

本文主要考虑季节温差以及混凝土收缩产生的当量温差，将两者叠加得到综合温差的取值。

(3)温度折减系数

温度折减系数κ按以下原则计算:对于不容许出现裂缝的结构，可不考虑裂缝对刚度的折减，仅考虑混凝土徐变及塑性性质的影响，温度折减系数可取κ=R·γ'，R为松弛系数，γ'为塑性系数，两者的具体计算参见文献［15］;对于容许出现裂缝的结构，裂缝对刚度的折减已考虑混凝土塑性性质，计算温度效应时仅需考虑混凝土徐变及裂缝对刚度的折减，温度折减系数可取κ=R·β，β为刚度折减系数。

(4)计算温差确定

从本工程大底盘双塔结构的实际情况出发，在小震下，结构构件不允许出现裂缝，故采用松弛系数和混凝土塑性变形影响系数确定计算温差，根据相关公式可求得松弛系数R=0.409;考虑最不利影响(构件最大截面h=1 000 mm)得出混凝土塑性变形影响系数为0.79，故本工程温度折减系数为 0.409 ×0.79=0.323，将综合温差乘以温度折减系数即可得到计算温差－37.7×0.323=－12.18℃，考虑工程计算中误差，将计算温度取为－13℃。

4 计算分析

4.1 考虑温度作用的双塔结构整体分析

在温差－13℃均匀温度场下的双塔结构进行振型分解反应谱分析，近似模拟双塔结构夏季施工，冬季使用时结构在刚度形成后所产生的温度残余应力对结构抗震性能的影响。

作为一个空间整体结构，模型中考虑了楼板和梁柱构件相互约束的作用，在计算温差－13℃作用下，以E轴线处的一榀框架为例，对考虑和不考虑温度效应的双塔结构的结楼层层间位移角进行比较，如图3所示。

从图3看出:在考虑温度和不考虑温度时，结构的塔楼部分层间位移基本相同，只是在裙楼顶端与塔楼顶部几层结构的楼层位移有一定的区别。根据模型计算出的结果，在均匀温度作用下，结构的地震楼层剪力、弯矩都变化不大，说明均匀温度的变化对于结构的影响相比较于地震作用来说是微小的，对结构的整体抗震性能影响不大。

4.2 结构构件内力分析

本节讨论大底盘双塔结构在温度和地震作用双工况下结构构件的受力情况，为便于分析，对结构平面图中的梁和柱进行编号，柱的编号用横竖轴线表示，梁的编号根据轴线来进行定位，如:A轴线上的第一跨梁用“梁A1－2”表示。“工况1”和“工况2”分别代表不考虑温度作用和考虑温度作用的情况。本文取有代表性的框架或者构件来定量地比较，以确定双塔结构在温差和地震作用下的结构响应。

(1)框架柱内力分析

从结构整体的角度上来看，在受整体均匀温度的作用下，结构是可以沿竖向自由伸缩的，因此，在温度作用下结构的轴力变化不大，而仅仅在底层约束最强处有局部微小的变化，在结构设计时，可不予考虑。

均匀温度场对双塔结构的影响主要体现在超限的群房大底盘上，选取群房D轴上的D1、D2、D3、D5、D7、D10柱进行考虑温度作用的地震反应分析，如图4所示。

在考虑温度作用时，底部两层柱的剪力发生了明显的变化，在第三、四、五层，柱的最大剪力与不考虑温度作用时基本相同。这是由于结构在均匀温度场作用下受到底部固端支座约束的影响，产生了较大的温度应力，但随着这种约束作用往上递减，温度应力迅速减小。说明均匀温度场对双塔结构大底盘的影响主要集中在底部两层。

取 B 轴首层的 B1、B3、B5、B7、B9、B11 柱对温度作用的影响作定量地分析，如表1所示:

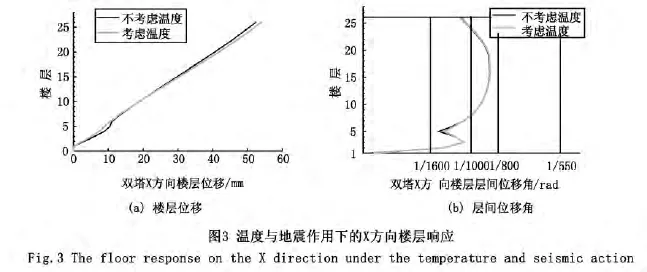
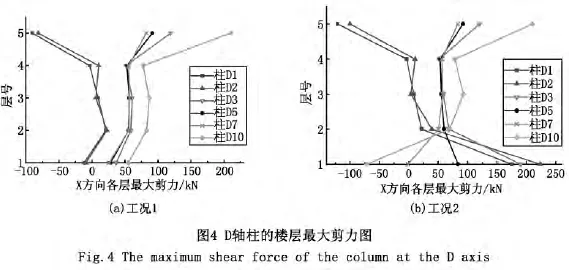
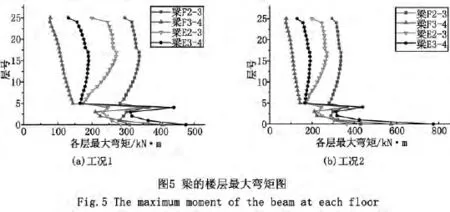
表1 温度和地震共同作用下B轴底层柱最大值(kN)Tab.1 The maximum internal force of the column base under the temperature and earthquake at the B axis

裙楼部分X方向其余各榀底层框架柱的变化趋势与此相近。由表1可以看出，由边柱至中柱剪力递减，至中间跨，柱所受的剪力与不考虑温度作用相差不大，体现了结构在温度作用下的自平衡性。柱剪力是由梁的轴向伸缩引起的，梁的轴向力由边跨至中跨逐渐抵消导致了柱剪力的递减。均匀温度场很大程度改变了结构底层柱的内力分布。

(2)框架梁内力分析

框架梁作为受弯构件，主要承受结构楼面的荷载并将其传递给框架柱。在地震力作用下，框架梁将地震力传递给竖向受侧力构件，使结构成为有效的空间协同工作体系;在双向地震和均匀温度作用下，选取塔楼部分的梁F2－3、梁F3－4、E2－3、E3－4，对其各楼层的最大弯矩进行分析，如图5所示。图中所取梁的楼层最大弯矩均为支座处的负弯矩。

与地震单独作用时相比，在均匀温度和地震共同作用下，梁的层最大弯矩依然只在结构底部两层变化较为明显，在上部塔楼部分，两种工况下的内力基本相同，如图5(b)所示。均匀温度对梁的弯矩的影响主要集中在底层梁柱结点处，在设计时应重视底层梁柱之间的连接构造。

(3)剪力墙应力分析

剪力墙是高层结构中主要的抗侧力构件，对控制结构的位移及改善构件的轴压比有显著的效果。本模型在双塔部分的核心筒处和两个塔楼外围角部都均匀地设有剪力墙，选取塔楼1外侧剪力墙5E－E1和4轴上核心筒处的剪力墙进行分析。

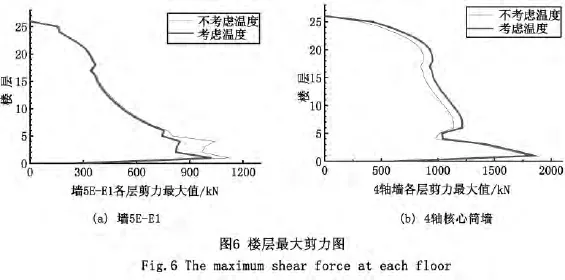
由图6可以看出，在双向地震作用下，温度对核心筒和外围剪力墙的影响是不一样的，在核心筒处，温度作用对底盘部分墙的楼层剪力影响不大，而对上部塔楼部分有不利的影响，会使得剪力墙楼层剪力增大;相反，塔楼的外围剪力墙对结构的影响主要集中在底部裙楼部分，考虑温度作用时，大底盘的楼层剪力变小，对结构是有利的。

5 结论

大底盘双塔结构在地震作用和均匀温度作用下，相对于塔楼，底盘在整体结构中有更多更复杂的受力形式和影响因素，因此，底盘也是双塔结构抗震设计的关键;温度效应对结构的抗震性能影响不大，但对于结构的局部构件特别是底部两层的内力影响较大;温度应力对结构构件的影响主要表现在框架梁的轴向的应力上，而对结构抗震性能的影响主要表现在柱和剪力墙的剪力和弯矩上;整体降温时，在结构底部两层，框架梁的轴力从边跨到中间跨递增;由于落地剪力墙受温度应力的影响较大，在很大程度上会削弱落地剪力墙的抗剪能力，致使底层框架柱承担更多的地震剪力，在设计时应予以注意。

［1］楼梦麟，张喜，林巧.水平地震下双塔楼结构的行波地震反应分析［J］.力学季刊，2012，33(1):137－145.

［2］LIM J，BIENKIEWICZ B.Effects of structural and aerodynamic couplings on the dynamic response of tall twin buildings with a skybridge［J］.ASCE，2009，9(1):1 －9.

［3］LIM J，BIENKIEWICZ B，RICHARDS E.Modeling of structural coupling for assessment of modal properties of twin tall buildings with a skybridge［J］.Journal of Wind Engineering and Industrial Aerodynamics，2011，99(5):615－623.

［4］GB50010－2010，混凝土结构设计规范［S］.

［5］CHEN H T，LIN J Y.Application of the hybrid method to transient heat conduction in one－dimensional composite layers［J］.Computers and Structures，1991，39(5):451－458.

［6］KULIKOV G M，PLOTNIKOVA S V.Heat conduction analysis of laminated shells by a sampling surfaces method［J］.Mechanics Research Communications，2014(55):59－66.

［7］THRELKELD J L.Themral enviormnental engineering［M］.Englewood Clibs，NJ:Prentice － Hall，1970.

［8］KAUSHIKA N D，SHMARA P K.Solar thermal analysis of honey comb cover system for energy conservation in an air conditioned building［J］.Energy and Buildings，1992(18):45－49.

［9］DVAIES G.Solutions to fourier equation and unsteady heat flow through structures［J］.Building and Environment，1995，30(3):309 －321.

［10］张国新.大体积混凝土结构温度场与温度应力仿真分析程序包SAPTIS编制说明及用户手册［M］.北京:中国水利水电科学研究院，2009.

［11］刘兴法.混凝土结构的温度应力分析［M］.北京:人民交通出版社，1991.

［12］赵 娟.超长高层建筑结构温度问题研究［D］.郑州:郑州大学，2002.

［13］宋琛琛，于明博.考虑温度应力的某大底盘双塔结构裙楼楼板地震反应分析［J］.佳木斯大学学报，2014，32(5):691－695.

［14］GB50009－2012，建筑结构荷载规范［S］.

［15］代慧娟.大型火电厂主厂房混凝土结构温变响应研究［D］.西安:西安建筑科技大学，2011.