假设检验在建设工程实验室管理中的应用

马蓉，朱海群，陈颉

(1.新乡市高新建设工程质量检测有限公司，河南 新乡453000;2.新乡市市政设施管理处，河南新乡453000)

在建设工程实验室管理中，人员素质与水平的考察对实验室是至关重要的。一个实验室的水平高低优劣，很大程度上取决于人员素质与水平［1］。根据规定［2］，在建设工程实验室管理中，经常需要开展能力验证、人员比对、操作观察来证明人员能力。温巧夫［3］采用t检验法证明手机电池的“下模宽度”，对关键质量特性造成显著性影响，需要重点改善。郝项超［4］采用偏最小二乘logistic方法对企业财务危机进行预测，检验显示预测结果更加稳健和可靠。本文以数理统计学［5］的假设检验理论为依据，应用多种假设检验的方法对采集的实验数据进行量化分析，来评定实验操作过程对实验结果影响有无显著性差异。

1 假设检验的理论依据

一般来说，若某一随机变量是受多种相互独立的随机因素的影响，而每一种随机因素所起的作用又是极其微小的，那么该随机变量就近似服从正态分布［6］。实验室的检测数据看来毫无规则，但它们在总体上服从正态分布。

1.1 样本数据服从正态分布的证明

采用P－P图检验，可以直观显示样本数据是否符合正态分布。观察正态P－P图，如果变量服从正态分布，则实际累计概率与理论累计概率应该基本一致，则图中数据点应和理论直线(对角线)基本重合［6］。同时采用 Kolmogorov－Smirnov单样本检验法对样本数据进行正态分布检验，证明样本数据总体服从正态分布。

1.2 两批试验服从同一分布的证明

采用两个独立样本Mann－Whitney Test检验法，通过检验两个总体分布各自的中心位置是否相同，证明两批实验数据是否取自同一总体。如果两个总体分布的中心位置相同，则两个样本中各数据的秩次都应当围绕着平均秩次(N+1)/2均匀分布;如果和该理论值差别较大，则可以推断总体的中心位置是有差异的［6］。

如果计算结果的显著性水平＞0.05，接受假设检验;则两批实验数据取自同一总体，实验设备不随时间变化，不必调整实验设备。反之则拒绝假设检验。

1.3 数据的随机性证明

采用游程Runs检验法检验数据的随机性，检验两人的操作方法对实验结果影响有无显著差异。游程Runs检验用于判断样本数据的顺序是否为随机［6］。如果计算结果的显著性水平 ＞0.05，接受假设检验;两人得到的实验数据随机性无显著差异，证明两人的实验操作方法无本质的差别，实验数据是随机产生的。如果显著性水平＜0.05，则拒绝假设检验，说明实验可能存在系统误差或随机误差，此时需要对计算结果中显著性水平低的操作人员调整操作方法，找出问题的症结，从而改进实验室的管理水平。

2 实验方法

计算工具采用SPSS12.0进行计算。假设显著性水平α=0.05。试验机采用经过技术监督部门检定合格的同一台实验设备，试验机型号为天辰WDW－10。实验材料采用耐碱玻璃纤维网布。检测项目为经向和纬向的初始拉伸断裂强力(N/50 mm)，检测标准采用 JGJ144－2004、GB/T 7689.5－2001。参加实验人员为茹女士和孟女士。

根据检测标准［7］规定，试样制备尺寸为宽度50 mm、长度350 mm;试样数量纬向、经向各10片;拉伸速度100 mm/min;实验环境温度23℃ ±2℃，相对湿度50% ±10%;夹具间的有效长度为200 mm±2 mm。操作时，将试样放入一夹具中，使试样的纵向中心轴线通过夹具的前沿中心，在整个试样宽度上均匀地施加预张力，然后拧紧另一夹具，预张力为预计强力的1% ±0.25%。启动活动夹具，拉伸试样至破坏，记录最终断裂强力。

3 实验结果与分析

3.1 单样本K－S检验结果分析

从表1可见，单样本K－S检验结果中，茹女士的经向、纬向统计量Z值分别低于孟女士的经向、纬向统计量Z值，经向、纬向近似显著性概率均高于孟女士的经向、纬向近似显著性概率。如果原假设成立，则从这样一个正态分布的总体中按照现有样本量进行经向、纬向抽样，平均每100次中会有96.6次和80.9次得到实际数据和理论分布之间的差值K等于甚至大于现有样本的K值，这显然是一个很平常的事情。因此，样本数据服从正态分布的假设。

而孟女士的经向、纬向近似显著性概率有点偏低。从这样一个正态分布的总体中按照现有样本量进行经向、纬向抽样，平均每100次中会有60.0次和74.9次得到实际数据和理论分布之间的差值K等于甚至大于现有样本的K值，样本数据有点偏离正态分布。可以判定孟女士的实验操作过程出现了异常，应该根据实验室制定的程序文件和操作手册进行纠偏。

从图1中观察茹女士的经向正态P－P图，可见图中数据点和理论直线(对角线)基本重合。继续观察茹女士的趋势正态P－P图，茹女士的经向拉力值实际分布和理论分布相差很小，数据点较均匀的分布在y=0这条直线的上下，其残差绝对值基本不超过0.05，因此可以判定茹女士的经向拉力值基本上服从正态分布。

表1 单样本K－S检验结果Tab.1 Single－sample K －S test results

从图2中观察孟女士的经向正态P－P图，可见图中数据点和理论直线(对角线)基本不重合，经向数据点实际分布呈水平直线状，孟女士的经向拉力值实际分布和理论分布相差较大。继续观察孟女士的趋势正态P－P图，残差有非常明显的波动趋势，且多数绝对值超过0.1，由此可见，变量的原始数据与正态分布的理论数据相差较大，可以判定其有点偏离正态分布。

图3中观察茹女士的纬向正态P－P图，可见图中数据点和理论直线(对角线)基本重合，有个别数据点偏离对角线较远。继续观察茹女士的趋势正态P－P图，茹女士的纬向拉力值实际分布和理论分布相差不大，数据点较均匀的分布在y=0这条直线的上下，其残差绝对值多数不超过0.05，因此可以判定茹女士的纬向拉力值基本上服从正态分布。

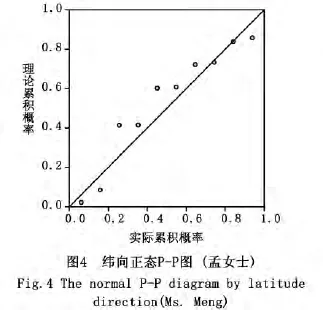
图4中观察孟女士的纬向正态P－P图，可见图中数据点和理论直线(对角线)基本不重合，纬向数据点实际分布呈水平直线状，孟女士的纬向拉力值实际分布和理论分布相差较大。继续观察孟女士的趋势正态P－P图，可见孟女士的纬向拉力值实际分布和理论分布相差较大，残差有非常明显的波动趋势，其残差绝对值多数超过0.05且部分绝对值超过0.1，由此可见，变量的原始数据与正态分布的理论数据相差较大，可以判定其有点偏离正态分布。

根据实验分析结果，孟女士承认在用拉力机进行实验时，未将夹具加紧耐碱玻璃纤维网布，夹具与耐碱玻璃纤维网布之间出现滑动，引起了实验结果异常，实验受人为因素影响大。

表2 2个独立样本Mann－Whitney检验结果Tab.2 Two independent samples Mann －Whitney test results

表3 数据随机性游程Runs检验Tab.3 Data randomness Runs test

因此，通过单样本K－S检验结果和正态PP图，可以判定实验数据是否服从或近似服从正态分布，可以判定实验过程是否处于受控状态。

3.2 两个独立样本Mann－Whitney检验结果分析

从表2可见，经向和纬向的精确显著性概率(双尾)分别为0.853和0.796，都大于给定的显著性水平0.05，证明茹女士和孟女士的实验数据确是取自同一总体，则实验设备不随时间变化，不必调整实验设备，实验过程没有显著性差别。

3.3 数据的随机性检验结果分析

由表3可见，茹女士经向和纬向相应的近似显著性概率分别为1.000和0.737，孟女士经向和纬向相应的近似显著性概率分别为0.737和0.314，显然两人的显著性概率均大于所设定的显著性水平0.05，因此不能拒绝原假设;但是茹女士的显著性概率远大于孟女士，可以认为茹女士的实验数据独立性更好一些，收集到的数据的顺序是不相关的;而孟女士收集到的实验数据独立性就差很多。这时就要提醒孟女士注意检查实验数据采集过程是否异常了。

4 结论

1)采用P－P图检验，可以直观显示样本数据是否符合正态分布，可以判定实验操作过程是否出现了异常。

2)采用Kolmogorov－Smirnov单样本检验法可以对样本数据进行正态分布的检验。

3)采用两个独立样本Mann－Whitney Test检验法，通过检验两个总体分布各自的中心位置是否相同，可以证明两批实验数据是否取自同一总体。

4)采用游程Runs检验法检验数据的随机性，可以检验两人的操作方法对实验结果影响有无显著差异。

5)评估实验过程是否有本质的差别，可以应用假设检验的方法进行量化分析。通过多角度对实验数据的量化分析，可以评定实验操作过程对实验结果影响有无显著性差异，评定实验数据采集过程是否出现异常，据此可以促进实验室管理。

［1］国家认证认可监督管理委员会.实验室资质认定工作指南［M］.北京:中国计量出版社，2010.

［2］国认函［2006］141号，实验室资质认定评审准则［S］.

［3］温巧夫，李敏强，王海波.假设检验在6σ管理中的应用［J］.科技管理研究，2004，11(5):194.

［4］郝项超，梁琪.企业财务危机预警:偏最小二乘logistic方法的应用［J］.管理工程学报，2010，24(5):100.

［5］茆诗松，王静龙，濮晓龙.高等数理统计［M］.北京:高等教育出版社，2004.

［6］张文彤.SPSS12.0统计分析基础教程［M］.北京:高等教育出版社，2004.

［7］GB/T7689.5－2001，玻璃纤维拉伸断裂强力和断裂伸长的测定［S］.