一种基于MSE变换的变步长恒模盲均衡改进算法

郭 强，姜 晖

(电子工程学院,安徽 合肥 230037)

一种基于MSE变换的变步长恒模盲均衡改进算法

郭 强，姜 晖

(电子工程学院,安徽 合肥 230037)

分析了军事通信中传统恒模盲均衡算法(CMA)的基本原理，并针对此算法收敛速度慢、收敛速度与稳态剩余误差之间存在矛盾的缺点,提出一种改进的变步长恒模盲均衡算法(VASCMA)。理论分析和实验仿真证明改进后的算法较传统算法具有更好的收敛效果。

盲均衡；恒模算法；收敛速度；剩余误差；变步长

0 引言

随着现代战争的发展，作战环境日趋复杂，确保复杂电磁信号环境下可靠、稳定、快速的军事通信是信息作战的重要内容。然而，通信信号在传输过程中，常会因为信道畸变而产生码间干扰(ISI)，这严重影响了接收信号的质量，降低了军事通信的可靠性和稳定性。因此，必须使用可靠的均衡技术对信道引起的畸变进行校正，以消除或减少ISI的影响[1]。盲均衡不需要发射端发送训练序列，可仅利用接收信号对畸变信道进行有效校正，降低传输误码率，是目前飞速发展的数字通信系统中的关键技术之一，在现代军事通信中有着非常广泛的应用[2-3]。20世纪80年代，Godard[4]和Triechiar[5]等学者提出了恒模算法 (CMA)，它是一种在军事通信中被广泛应用的盲均衡算法，但其存在以下不足[6]：1)对高斯噪声无免疫性；2)易陷入局部极小点，收敛速度较慢；3)迭代步长恒定，存在收敛速度与稳态误差之间无法平衡的矛盾。

本文针对传统CMA算法收敛速度慢、收敛速度与稳态误差间存在矛盾的缺陷，提出一种基于MSE变换的变步长恒模盲均衡算法(VASCMA)，它以均衡器输出的均方误差(MSE)作为控制步长的参量，理论分析和计算机仿真证明该算法可以有效解决传统恒模算法中收敛速度与稳态剩余误差之间的矛盾，加快收敛速度，提升均衡性能。

1 恒模盲均衡算法(CMA)

CMA算法是Bussgang类盲均衡算法的一个特例，其中心思想是构造一个具有凹凸性质的代价函数，再通过算法调节均衡器的抽头系数使代价函数取得最大或最小值，以此来达到均衡的目的[7]。Bussgang类盲均衡器的原理如图1所示。

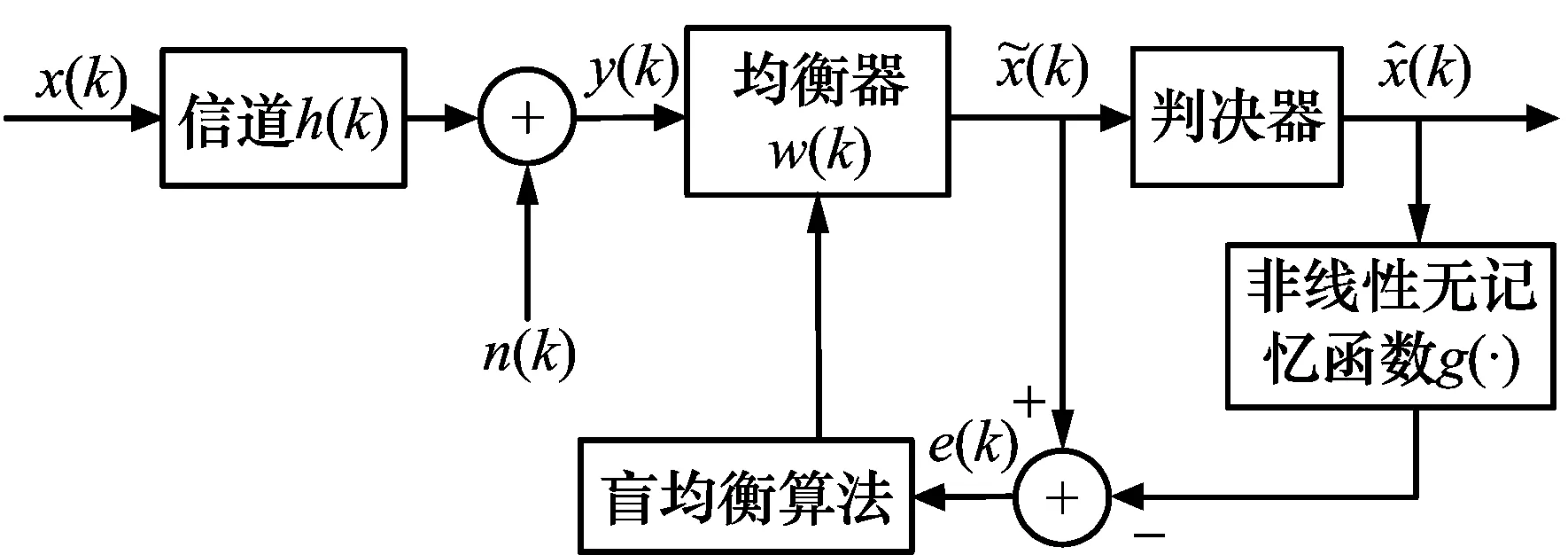
图1 Bussgang类盲均衡器的原理

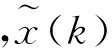
由图1可知，均衡器输出信号为：

式中，W(k)表示均衡器抽头系数向量，w(k)为均衡器抽头系数，N为输入数据总量。

误差函数为：

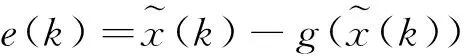
(2)

在CMA算法中，定义：

(3)

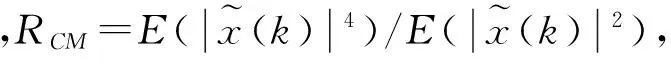
CMA算法的代价函数J(k)为:

(4)

算法的目标为代价函数J(k)的最小化，而由公式(4)可知，J(k)的取值取决于y(k)和w(k)，可将算法的目标看作是多维非凸曲面中求解最小值的问题，这是一个无约束最优化问题。

均衡器抽头系数的迭代公式为：

(5)

式中，μ表示迭代步长因子，通常取足够小的恒定值。

将式(3)代入式(5)得：

(6)

2 改进的变步长恒模盲均衡算法(VASCMA)

在算法收敛初期，均衡关心的问题是算法能否收敛，因此希望使用大步长促使算法尽快收敛；而随着算法的逐步收敛，均衡期望获得更好的收敛性能，因此希望步长减小以降低稳态剩余误差，提高收敛精度。

传统CMA算法中，步长因子为恒定值，无法跟随迭代过程改变大小。这一原因导致算法中存在收敛速度和稳态剩余误差之间无法平衡的矛盾。变步长的思想因为简单、有效而被广泛应用于解决此矛盾。

在变步长CMA算法中，通常用来控制步长变化的参量有输出信号的功率、MSE、剩余误差的相关变化等。相对于其它几种改进算法，基于MSE变换的变步长CMA算法结构简单、计算量较小。

基于MSE变换的变步长CMA算法中，抽头系数的迭代公式为：

W(k+1)=W(k)-2μ(k)e(k)YH(k)

(7)

式中，μ(k)为可变步长，其迭代公式为：

μ(k)=αμ(k-1)+β(1-(exp(-ηE(e(k)2))))

(8)

式(8)中，步长μ(k)的取值与前次迭代中步长取值μ(k-1)和MSE的值有关，其中，α、η为待定参数，β为常数比例因子。为保证式(8)的收敛，β的选取必须保证e(k)的最大值小于步长的上界[8]，即：μ≤μmax=2/3trR，其中R为发送信号的自相关矩阵，trR为R的迹。

通过MSE控制步长因子可以保证在迭代初期，步长较大，算法尽快地进入收敛状态；而在算法逐步收敛过程中，MSE逐渐减小，步长也变小，有利于降低稳态误差，提高收敛精度。改进算法没有直接用剩余误差e(k)来控制步长μ，是因为算法刚开始运算时，稳态剩余误差较大，为保证算法的收敛性，比例因子β取值必定很小，这样步长就会随着迭代次数的增加而迅速变小，无法达到快速收敛的效果，而式(8)中α的存在可以控制步长的改变速率，促使算法实现快速收敛[9]。

根据以上分析可知，变步长思想的引入有效解决了传统CMA算法中收敛速度和稳态剩余误差之间的矛盾，保证在不增加稳态误差的前提下提高算法的收敛速度，提升均衡效果。

3 实验仿真

3.1 仿真条件

为了验证改进算法在军事通信盲均衡中的性能，对VASCMA算法和传统CMA算法的收敛速度、剩余码间干扰进行了仿真分析。在仿真实验中，设置的均衡器、发射信号和传输信道模型的参数如下：均衡器抽头数为11，采用中心化初始策略，即中心抽头系数初始值为1，其它抽头系数初始值取0；传统CMA算法中，μCMA=0.0001；VASCMA算法中，步长初始值μVASCMA=0.0001,α=0.5，β=0.002，η=50；信噪比20dB；发送信号的调制样式分别为4PSK和4QAM，发送符号数为10000；用400次蒙特卡洛仿真的统计平均值来评价几种算法。

三种信道的冲击响应函数如下：

信道1[10]：h=[0.3132，-0.104,0.8908,0.3134]，为多径水声信道。

信道2[11]：h=[0.05,-0.063,0.088,-0.126,-0.25,0.9047,0.25,0,0.126,0.038,0.08]，为数字离散信道。

信道3[12]：h=[0.05,0.1+0.15i,0.9-0.15i,0.15,-0.2+0.2i,0.1+0.2i,-0.1+0.15i]，为无线数字通信信道。

3.2 仿真结果分析

图2和图3分别给出了4PSK信号、4QAM信号通过信道1时两种算法的学习曲线。由图2可知，当输入信号为4PSK调制样式时，VASCMA算法经过2000次左右的迭代即可收敛，而传统的CMA算法需经过大概5000次迭代才可以达到收敛，通过对比，可知在信道1下，改进算法较传统算法对4PSK调制信号的均衡速度更快；另外，对比两种算法收敛后MSE的值可知，改进算法的稳态剩余误差更稳定，有效克服了传统CMA算法中收敛速度和稳态剩余误差之间的矛盾。从图3中，也可知改进算法较传统CMA算法收敛速度更快，收敛精度更高。

图4、图5分别给出了4PSK调制信号通过信道2、信道3时两种算法的学习曲线，图6为4PSK信号通过信道3时改进算法的步长变化曲线，由图可知：

1)VASCMA算法无论在收敛速度还是稳态剩余误差方面都优于传统CMA算法。

2)VASCMA算法在收敛初期，MSE较大，步长μ取值也较大，这方便实现快速均衡；随着VASCMA算法接近收敛，MSE逐渐减小，步长μ也趋于稳定，这有利于降低稳态误差，提高收敛精度。

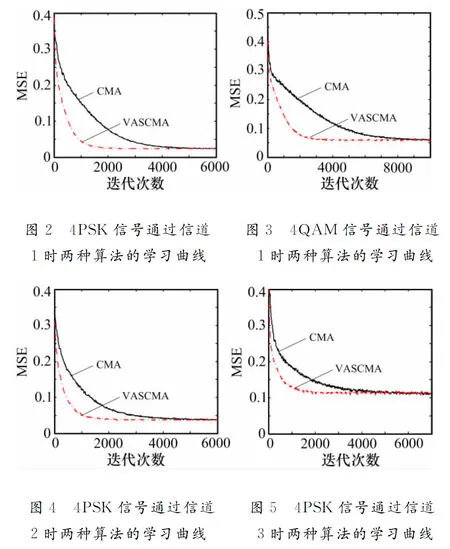
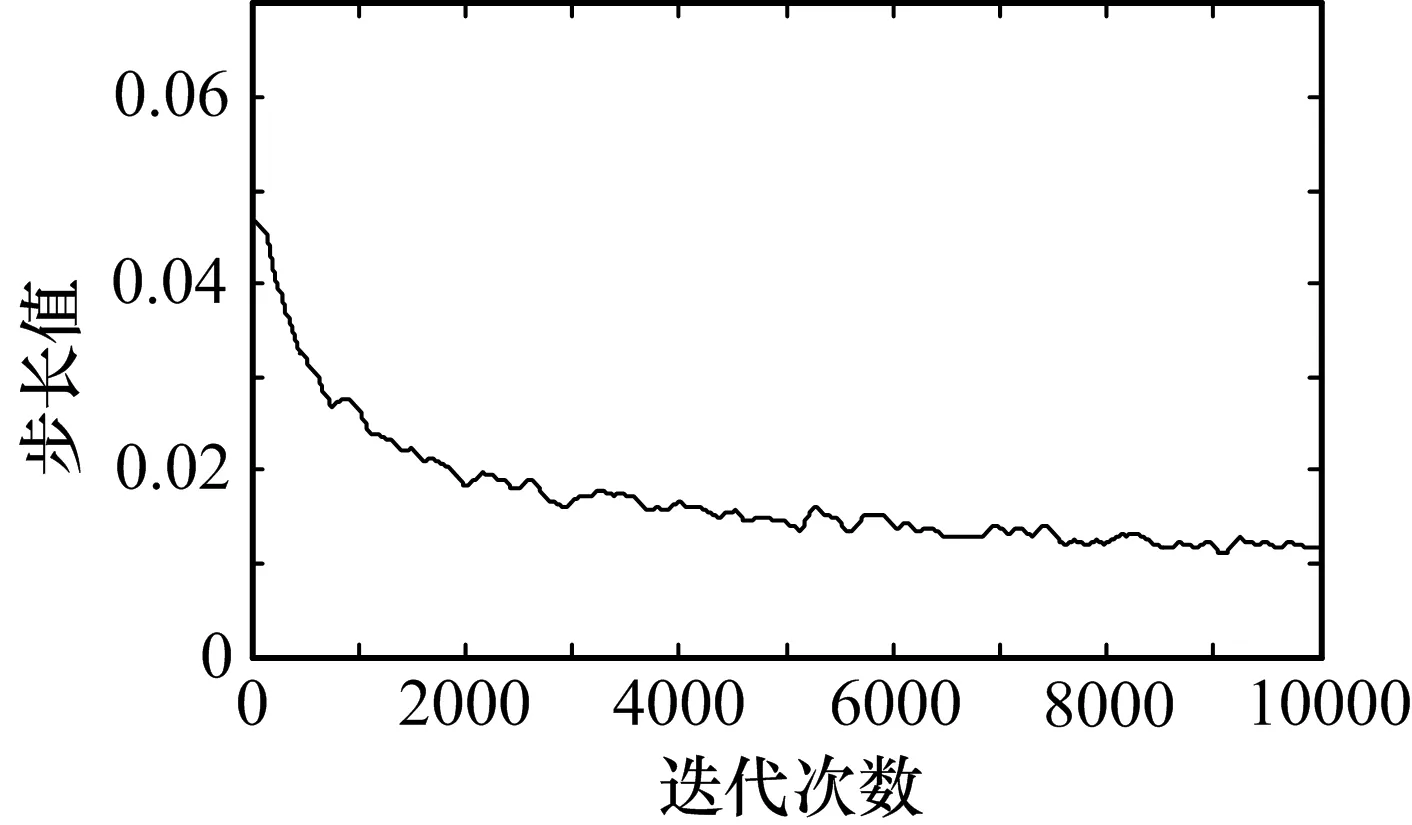
图6 4PSK信号通过信道3时改进算法的步长变化曲线

图7、图8给出了4PSK信号通过信道1前、后的星座图，由图可知，信号通过信道1后产生了严重的码间干扰，导致星座图非常分散，信号难以辨认。图9和图10为均衡后两种不同算法下信号的星座图，通过对比可知，VASCMA算法的星座点更集中，能更好地收敛至信源点附近，即改进后算法的稳态剩余误差和误码率更小。

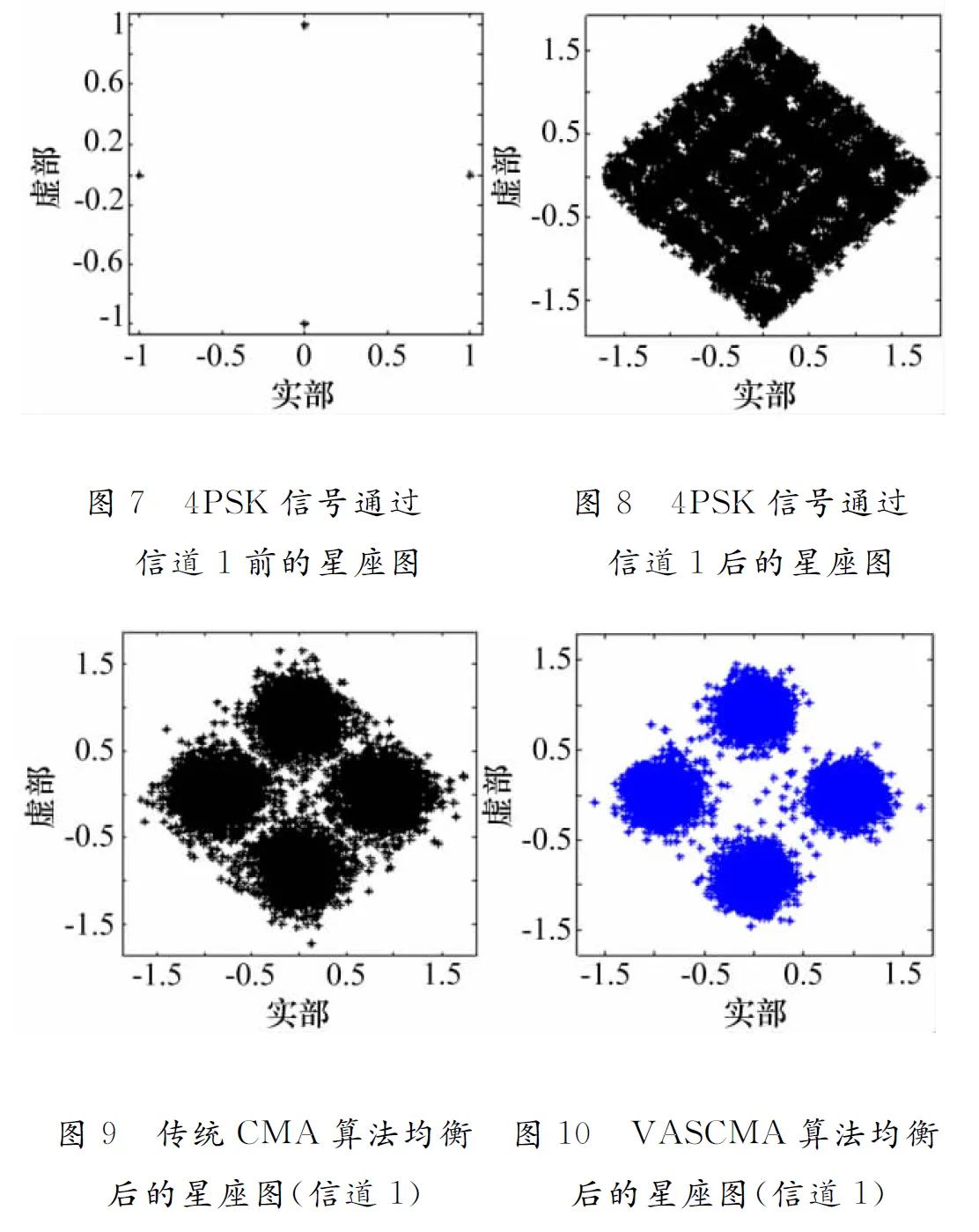
图11、图12为4PSK信号通过信道3，经过两种算法均衡后的星座图。可以发现经过VASCMA算法均衡后的输出信号星座图集中度更好，更加清晰可辨，即改进算法的稳态剩余误差和误码率更小。

虽然VASCMA算法能有效克服收敛速度和稳态剩余误差之间的矛盾，但其仍然存在一些不足之处。图12中，信号在通过信道3后发生了明显的相位偏转。这是因为信道3为多径无线数字信道，而改进算法仅包含信号的幅度信息，对相位信息并不敏感，所以，在通过信道3后，输出信号的星座相位发生了偏移。若要纠正该缺陷，后面可加大对修正恒模(MCMA)等算法的探究，将信号的相位信息引入算法的代价函数中，实现算法对相位偏差的有效纠正。

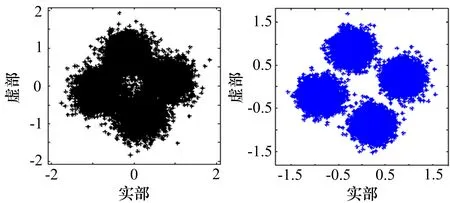
图11 传统CMA算法均衡后的星座图(信道3) 图12 VASCMA算法均衡后的星座图(信道3)

4 结束语

本文针对传统恒模算法收敛速度慢、收敛速度与稳态剩余误差之间存在矛盾的缺陷，提出了一种基于MSE变换的变步长恒模算法，并分别在3种不同信道下，对改进前后算法的性能进行分析、比较。仿真结果表明，改进后的算法较传统恒模算法具有更快的收敛速度，更小的稳态剩余误差，更好的收敛效果。但发送信号在通过多径无线通信信道时，相位会发生偏移。在保证算法收敛速度和精度的前提下校正信号的相位偏移将是下一步的研究重点。■

[1] 华亚维.短波数据传输自适应均衡技术研究与实现[D].西安：西安电子科技大学,2009.

[2] 杨宾,王大磊,吴瑛,等.利用无约束函数的QAM 信号自适应盲均衡方法[J].信号处理，2014，30(4)：399-404.

[3] 邱天爽,魏东兴.通信中的自适应信号处理[M].北京：电子工业出版社,2005.

[4] Godard DN.Self-recovering equalization and carrier-tracking in two-dimensional data communication systems[J].IEEE Trans.Commun.,1980,28(11):1867-1875．

[5] Treichiar JR，Agee B.A new approach to multi-path correction of constant modulus signals[J].IEEE Trans. ASSP,1983,31(2):459-471．

[6] 钟华,金国平,郑林华.一种新的修正步长盲均衡算法[J].系统仿真学报,2009(9).

[7] 张丹丹.盲均衡算法及其FPGA实现的研究[D].秦皇岛：燕山大学,2013.

[8] 高丽娟,赵洪利,蒋太杰.一种改进的变步长常数模算法[J].电子与信息学报,2007,29(2):283-286.

[9] 孟新红,欧阳慧勇.一种新的变步长恒模盲均衡算法[J].通信技术,2012(9):39-42.

[10]王峰.基于高阶统计量的水声信道盲均衡理论与算法[D].西安：西北工业大学，2003.

[11]赵雅兴,刘栋,张宁.一种适用于FPGA实现的盲均衡算法[J].通信学报,2001,22(8)：108-111.

[12]敖卫东.短波信道自适应盲均衡算法研究[D].长沙:国防科学技术大学,2007.

An improved CMA with varying step-size based on MSE

Guo Qiang, Jiang Hui

(Electronic Engineering Institute，Hefei 230037，Anhui，China)

The basic principle of the traditional constant modulus blind equalization algorithm (CMA) is analyzed，and an improved CMA with varying step size (VASCMA) is put forward according to CMA’s defect that it has a slow rate of convergence and a contradiction between the convergence rate and accuracy. Theoretical analysis and simulation results show that the improved algorithm has better convergence effect and performance than the CMA.

blind equalization；CMA；convergence rate；residual error；variable step-size

2014-10-13；2014-11-24修回。

郭强(1989-)，男，硕士研究生，研究方向为通信信号的自适应处理。

TN975

A