基于Fisher判别分析的冲击地压危险性等级预测
邵良杉 徐 波(辽宁工程技术大学系统工程研究所,辽宁 葫芦岛 125000)
基于Fisher判别分析的冲击地压危险性等级预测
邵良杉 徐 波(辽宁工程技术大学系统工程研究所,辽宁 葫芦岛 125000)
针对矿井中发生的冲击地压危险性分级问题,应用因子分析和Fisher判别分析理论,选取煤层厚度、煤层倾角、埋深、构造情况、煤层倾角变化、煤层厚度变化、瓦斯浓度、顶板管理、卸压、响煤炮声为影响因素,分析影响因素之间的相关性,对相关性较强的因素进行因子分析,提取恰当的公共因子,进而建立基于因子分析的冲击地压危险性等级Fisher判别分析(FDA)模型。利用四川砚石台煤矿23组实测数据作为学习样本对模型进行训练。采用回代估计法检验模型的有效性,回判的误判率为0。将另外未参加训练的12组煤矿动力现象数据作为测试样本,对其危险性等级进行预测,并与传统的Fisher判别方法进行对比。结果表明,经过对样本因子分析后,指标个数减少,相关性降低,可以有效预测冲击地压的危险性等级,用该模型所得到的预测结果的误判率为0。
冲击地压 预测 分级 因子分析 Fisher判别分析 回代估计法
冲击地压是矿井中一种较为典型的灾害现象,它是聚积在矿井巷道和采场周围煤岩体中的能量突然释放,造成煤岩体振动和破坏、巷道跨坏、设备和支架损坏甚至人员伤亡的一种动力灾害现象。冲击地压还可能引发瓦斯爆炸、火灾、水灾,破坏通风系统,甚至会造成地震和居民房屋、建筑物破坏等灾害。因此,冲击地压已经成为煤矿中重大灾害之一[1-3]。世界上很多采煤国家,如英国、波兰、印度、南非、德国等都有冲击地压事故的发生[4-5],最早的冲击地压事故煤矿是1738年发生在英国的南斯塔福煤田。自从1933年在抚顺胜利煤矿发生冲击地压事故以来,我国有30%以上的国有重点煤矿也都发生过冲击地压的灾害[6],包括北京、枣庄、开滦、徐州、阜新、大同、鹤壁、鸡西、七台河、淮南、大屯、鹤岗、义马、平顶山等百余个矿井[7-8]。我国煤矿中发生的冲击地压除了瞬时震动性、突然性和破坏性等显著特征外,还具有以下特点:①发生条件极为复杂;②类型多种多样,灾害严重程度不同;③随着矿井开采深度的增加,越来越多的矿井发生冲击地压灾害,造成的危害也愈来愈重[9]。冲击地压的预测和防治具有重要的实用价值和现实意义,已成为矿山安全生产中亟待解决的重大课题[10]。世界上许多国家都提出了对冲击地压进行预测的方法,比较有代表性的传统方法有采用经验类比分析法、钻屑法、地音监测法、微震监测法、含水率测定法、电磁辐射法等[11-12]。这些方法的特点是在应用的过程中只考虑了单一因素或主要因素。但冲击地压是一个复杂的动力学系统,它受到井下复杂的采矿地质条件和自然条件共同影响,存在一定的非线性和不确定性,因此用单一指标来进行预测会存在很多不足。为此,近些年,很多学者在考虑多因素影响的情况下,将神经网络[13]、PSO-SVM模型[14]、时间序列模型[15]等应用到冲击地压的预测中,使预测结果更加客观和准确。这些方法在实际应用中都有一定的成果,但是每种方法都存在一定的局限性,如神经网络容易陷入局部最优,对解决小样本问题能力有限;支持向量机的核函数及其参数的选择较为复杂;而时间序列在应用时常常忽略了外界因素的影响,因此,若外界发生较大变化时,会出现较大偏差。
1 因子分析与Fisher判别分析方法
1.1 因子分析的数学模型
因子分析主要目的是浓缩数据,通过对诸多变量的相关性研究,把一些信息重叠、具有错综复杂关系的变量归结为少数几个不相关的综合因子,是多元统计分析的一个重要分支。
设有k个变量,分别为X1,X2,…,Xk,其中,
即每个变量由n个指标构成,且每个变量都是标准化变量,即均值为0,标准差为1。因子分析的数学模型可以表示为
(1)
式中,Fj是公共因子,m(m X=AF+e, (2) 其中, 是负载矩阵。 因子分析的前提是X1,X2,…,Xk之间具有较高的相关性。判断变量之间是否适合作因子分析的方法主要有KMO样本测度法和巴特利特球体检验[16]。 在确定了公共因子变量之后,要计算这些变量在不同因子上的具体数据值,即因子值,以便进一步研究。设第j个公共因子的因子值是fj,可以根据X1,X2,…,Xk的样本值计算出来,计算公式如下: (3) 上式可以简记为 fj=xβj, 式(3)中,βkj是因子值的系数。因子值的求法一般有以下3步:①求出标准化数据xij的相关系数矩阵R;②从xij与负载矩阵A,利用公式 为负载矩阵的A的第j列,计算出βj;③由公式fj=xβj,计算出公共因子fj的因子值。 1.2 Fisher判别分析方法的求解过程和思路 Fisher判别分析的基本思想是投影[16-17],即将高维数据点投影到低维空间上,使数据点变得比较密集,从而克服由于维数高而引起的“维数祸根”[18]。投影的原则是将总体与总体之间尽可能地分开,然后根据类间距离最大、类内距离最小的原则确定判别分析函数,达到正确分类的目的,进而对新的样本进行分类判别。 设有m个总体G1,G2,…,Gm,每个总体的特征指标都是p个,相应的均值向量和协方差矩阵分别为μ1,μ2,…,μm(p维),V1,V2,…,Vm(p×p阶)。对于样本 假定其判别函数为 Y=u1x1+u2x2+…+upxp=uTx, (4) 其中,u为p维向量,Y为一维的随机变量。那么,Y在各类中的均值和方差分别为 ei=uTμi,i=1,2,…,m, (5) (6) 记B0为Y在各类中的均值ei的离差平方和: (7) B0反映的是均值ei之间的离散程度,B0的值越大,离散程度就越大,各个总体就越容易被划分开来。 记E0是Y在各类中的方差之和: (8) E0是Y在各类中的方差之和,其值越小,则G1,G2,…,Gm就越容易被划分开来。Fisher判别法的准则就是选择能够使B0/E0最大的u,来作为判别函数 Y=u1x1+u2x2+…+upxp=uTx 中的系数向量。令 设λ是矩阵[E-1B]的最大特征根,对应于λ的特征向量u就是所要求的判别函数中的系数向量。当存在大于或等于3个总体时,通常找出对应于[E-1B]的前几个较大特征根 λ1,…,λt,t≤min(m-1,p), 并根据衡量判别函数判别能力的指标——贡献率 进行分类,记 对于建立的FDA模型,要对其判别效果进行检验,模型的有效性主要表现在2个方面:①对已知类型的样本的回代判别正确率高,可以用回代估计法求误判率;②对未分类样本的判别正确率较高。 来自总体Gm,容量为nm的样本为 将所有的训练样本作为n1+n1+…+nt个新样本,依次代入建立的判别函数并进行判别,这个过程就是回判。知道总的误判个数N后,就可以求出误判率η,η的计算公式为 2.1 特征属性的选取及其相关性分析 影响矿井冲击地压危险的因素有很多,根据多年的工程经验,认为对冲击地压的重要影响因素主要分为地质因素(煤层厚度、煤层倾角、煤层倾角变化情况、煤层厚度变化情况、埋深、构造情况等)和开采因素(瓦斯含量、顶板管理、卸压、响煤炮声等)。以四川砚石台煤矿为例,结合砚石台煤矿的地质结构和冲击地压的重要影响因素,共选择10个影响砚石台煤矿冲击地压的因素,分别为煤层厚度(X1)、煤层倾角(X2)、埋深(X3)、构造情况(X4)、煤层倾角变化(X5)、煤层厚度变化(X6)、瓦斯浓度(X7)、顶板管理(X8)、卸压(X9)、响煤炮声(X10)作为冲击地压危险性分级评价指标。这些指标中,构造情况(X4)、煤层倾角变化(X5)、煤层厚度变化(X6)、顶板管理(X8)、卸压(X9)、响煤炮声(X10)是状态参量,为了进一步研究,要先将这些参量进行数量化处理,其赋值方法见表1。 表1 冲击地压危险性预测的状态参量指标分级与赋值Table 1 Classification and valuation of state parameter indexes in rock burst risk prediction 在砚石台煤矿多年来实测的各个指标和冲击地压危险性的数据中,选取具有代表性的35个样本,其中23个作为FDA模型的训练样本,如表2,另外12 作为预测样本进行判别检验,如表3。根据表2中的工程数据,利用SPSS17.0软件对这10个变量进行两两分析,得到检验结果为:构造情况、煤厚变化、顶板管理、卸压和响煤炮声相互之间的t统计量的值的显著性概率p<0.01,相关系数显著异于0,因此,彼此之间存在较强的相关关系;煤层厚度、煤层倾角、埋深、煤层倾角变化、瓦斯浓度相互之间以及与其他5个变量之间的t统计量的值的显著性概率p>0.01,相关系数不异于0,因此,彼此之间的相关关系较弱。 表2 FDA预测模型学习样本数据Table 2 Training sample data for the FDA forecast model 表3 FDA预测模型测试样本数据Table 3 Test sample data of the FDA forecast model 2.2 因子分析的KMO和Barlett检验 为了使指标的选择更加可靠,对存在较强相关关系的5个指标(构造情况、煤厚变化、顶板管理、卸压和响煤炮声)进行KMO和巴特利特球体检验。运行SPSS可得二者的检验结果:样本的KMO值为0.807,按照统计学家Kaiser给出的判断标准,KMO值在0.8~0.9,很适合作因子分析;巴特利特球体检验的显著性概率为0.000,小于显著性水平0.01,拒绝相关系数矩阵为单位矩阵的零假设,可以作因子分析。 2.3 FDA预测模型 矿井中发生的冲击地压危险性程度不等,根据造成的危险性情况来看,将砚石台煤矿发生的冲击地压危险性分为4个等级,分别为微冲击(T1)、弱冲击(T2)、中等冲击(T3)和强冲击(T4)。以表2中的23个样本作为训练样本,建立基于因子分析的FDA预测模型。将10个影响冲击地压的因素中的 5 个相关程度较高的指标进行因子分析,提取少数公共因子,实现对冲击地压影响因素的降维,用新得到的公共因子及 5 个相关程度较弱的指标作为FDA模型的判别因子。根据因子分析理论和Fisher判别分析理论进行训练和学习,用未参加训练的12个样本(见表3)对建立的FDA模型进行效果检验。 对训练样本进行因子分析可分为3个步骤: (1)提取合适的公共因子。将训练样本中的有较强相关性的构造情况、煤层厚度变化、顶板管理、卸压和响煤炮声5个指标作为因子分析的变量,运行SPSS17.0,根据得到的碎石图(见图1)和总方差解释表,前2个公共因子的累计方差贡献率为86.365%,说明,这2个公共因子可以解释原始5个变量的86.365%的信息。 图1 碎石图 (2)构造因子变量。确定提取2个公共因子之后,应用方差最大法对得到的负载矩阵进行正交旋转,可以得到旋转后的负载矩阵,见表4。正交旋转的目的是为了降低初始因子的综合性,以便更容易找出因子的实际意义。从表3中各个指标的因子得分可以看出,公共因子F1由构造情况、煤厚变化及顶板管理组成,公共因子F2由卸压和响煤炮声组成。 表4 因子载荷旋转Table 4 Rotation of factor loading (3)计算因子值。采用回归方法得到因子得分系数矩阵,如表5,进而可以计算出因子值。根据表5可以写出2个公共因子值的表达式分别为 F1=0.551X4+0.443X6-0.392X8+ 0.528X9+0.019X10; (10) F2=-0.314X4-0.216X6+0.157X8- 1.061X9+0.382X10. (11) 利用式(10)和(11)及表2中的变量值,计算出因子值,并将F1和F2作为新变量保存到表1中。 表5 因子值的系数Table 5 Factor score coefficient 由于煤层厚度、煤层倾角、埋深、煤层倾角变化和瓦斯浓度相互之间以及与另外5个变量之间的相关性较弱,所以将这5个变量(煤层厚度、煤层倾角、埋深、煤层倾角变化和瓦斯浓度)与2个公共因子(F1和F2)作为Fisher判别分析模型的判别因子。应用上述理论,可得到Fisher判别函数为 Z1(x)=-0.180X1+0.057X2+0.003X3+ 0.493X5+0.426X7+2.852F1+ 2.346F2-4.910, (12) Z2(x)=1.032X1+0.027X2+0.063X5- 0.902X7-0.134F1-0.612F2-3.119, (13) Z3(x)=0.217X1+0.055X2+0.004X3- 0.438X5+0.480X7-0.889F1+ 0.787F2-5.070. (14) 同时可以得到判别函数的附加特征值和组中心值如表6所示。可见,所得到的3个判别函数的判别能力是显著的。第1个判别函数的特征值为24.899,方差贡献率是94.9%,说明其判别效率非常高,可以解释样本94.9%的信息,同时,其正则相关系数为0.981。运用3个判别函数来对样本进行判别,可以使得累计方差贡献率达到100%,即可以解释样本全部信息,因此,利用3个判别函数能够进行更准确的判别。根据表6中的组中心值,以第1个函数为例,其在T1类冲击地压危险性(微冲击)的中心得分为-7.460,在T2类冲击地压危险性(弱冲击)的中心得分为-3.358,在T3类冲击地压危险性(中等冲击)的中心得分为0.408,在T4类冲击地压危险性(强冲击)的中心得分为5.502。以此为基础,可以通过比较待判冲击地压危险性等级的样本函数值与4类危险性等级类别的中心值的距离来判别新样本属于哪一类别。 为了检验建立的FDA模型的有效性,采用回代估计法计算误判率,将23组训练样本的数据代入到FDA模型中,得到的分类结果列入表2,与实际分类结果完全一致,误判率为0,证明模型的正确率高,是可靠的,可以运用到实际的工程项目中。 表6 Fisher判别函数附加特征值和组中心值Table 6 Additional eigenvalues and central values of Fisher discriminant function 2.4 模型的检验和实例分析 表7 FDA预测模型测试结果Table 7 Test results of the FDA forecast model (1)基于因子分析的Fisher判别模型的预测能力较强,科学合理,性能可靠,简便可行,适合预测矿井中冲击地压的危险性等级。 (2)应用因子分析理论研究影响矿井中冲击地压发生的因素,避免因素之间较强的相关性导致的某些信息重合,进而避免对建立的Fisher判别模型在判别样本类别时产生不利影响。 (3)利用反映原始变量(构造情况、煤层厚度变化、顶板管理、卸压和响煤炮声)大部分信息的公共因子F1和F2以及煤层厚度、煤层倾角、埋深、煤层倾角变化和瓦斯浓度共7个指标建立FDA模型,对冲击地压的危险性等级进行预测,模型学习效率高,预测精度高,预测结果与实际结果完全符合。对样本数据进行因子分析处理后,冲击地压危险性等级的判别精度比单纯使用Fisher判别法有较大提高。 (4)基于因子分析的FDA预测模型以有限的实测工程数据为基础,受到原始数据的典型性、代表性以及正确性的影响,同时,冲击地压是一个非常复杂的问题,受到多种因素的共同影响。因此,在实际工程应用中,应广泛收集资料,选取合适的样本数据,对模型进行训练,提高模型的训练精度以获得更加可靠的预测结果。 [1] 窦林名,何学秋.冲击矿压防治理论与技术[M].徐州:中国矿业大学出版社,2001. Dou Linming,He Xueqiu.Prevention Theory and Technology of Rock-burst[M].Xuzhou:China University of Mining and Technology Press,2001. [2] 姜耀东,赵毅鑫,刘文岗,等.煤岩冲击失稳的机理和实验研究[M].北京:科学出版,2009. Jiang Yaodong,Zhao Yixin,Liu Wengang,et al.Investigation on the Mechanism of Coal Bumps and Relating Experiments[M].Beijing:Science Press,2009. [3] 窦林名,何学秋.煤矿冲击矿压的分级预测研究[J].中国矿业大学学报,2007,36(6):717-722. Dou Linming,He Xueqiu.Technique of classification forecasting rock-burst in coal mines[J].Journal of China University of Mining and Technology,2007,36( 6):717-722. [4] 赵生才.深部高应力下的资源开采与地下工程-香山会议第175次综述[J].地球科学进展,2002,17(2):295-298. Zhao Shengcai.Deep resources exploitation and underground engineering under high stress-xiangshan conference for the 175th time[J].Advance in Earth Sciences,2002,17(2):295-298. [5] Bieniawski A T,Denkhaus H G,vogler U W.Failure of Fracture Rock[J].Rock Mech Min Sci,1969(6):323-341. [6] 国家煤矿安全监察局.“十一五”期间( 2006—2010 年)全国煤矿事故分析报告[R].北京:国家煤矿安全监察局,2011:7-10. China Administration of Coal Mine Safety.Report of the National Coal Mine Accidents in “Eleven Five” Period( 2006-2010)[R].Beijing:China Administration of Coal Mine Safety,2011:7-10. [7] Cook N G W.A note on Rock-bursts considered as a problem of stability[J].South Afr Int Min and Metallurgy,1965,65:437-446. [8] 孙 学.复杂开采条件下冲击地压及其防治技术[M].北京:冶金工业出版社,2009:3-4. Sun Xue.Under the Condition of Complicated Mining Impact Ground Pressure and Its Prevention and Control Technology[M].Beijing:Metallurgical Industry Press,2009:3-4. [9] 吴财芳,曾 勇.神经网络在冲击地压危险性预测预报研究中的应用[J].工程地质学报,2003,11(3):263-268. Wu Caifang,Zeng Yong.Application of neural networks to study and prediction forecast rock-burst[J].Journal of Engineering Geology,2003,11(3):263-268. [10] 何满潮,谢和平,彭苏萍.深部开采岩体力学研究[J].岩石力学与工程学报,2005,24(16):2803-2813. He Manchao,Xie Heping,Peng Suping.Study on rock mechanics in deep mining engineering[J].Chinese Journal of rock mechanics and engneering,2005,24(16):2803-2813. [11] 窦林名,何学秋.冲击矿压危险预测的电磁辐射原理[J].地球物理学进展,2005,20(2):427-431. Dou Linming,He Xueqiu.Monitoring rock burst by electromagnetic emission[J].Progress in Geophysics,2005,20(2):427-431. [12] 闵文江,卜凡启.煤矿冲击矿压及防治技术[M].徐州:中国矿业大学出版社,1998. Min Wenjiang,Bu Fanqi.Coal Mine Rock-burst and Prevention Technology[M].Xuzhou:China University of Mining and Technology Press,1998. [13] 孙凤琪.AdaBoost 集成神经网络在冲击地压预报中的应用[J].吉林大学学报:信息科学版,2009,27(1):79-84. Sun Fengqi.Rock-burst prediction modeling based on ensemble neural network[J].Journal of Jilin University:Information Science,2009,27(1):79-84. [14] 赵洪波,茹忠亮.冲击地压预测的PSO-SVM模型[J].岩石力学与工程学报,2007,26(S1):3479-3483. Zhao Hongbo,Ru Zhongliang.PSO-SVM model for prediction of rock burst[J].Chinese Journal of Rock Mechanics and Engineering,2007,26( S1):3479-3483. [15] 陶 慧.基于监测时间序列的冲击地压混沌特性分析及其智能预测研究[D].徐州:中国矿业大学,2013. Tao Hui.Chaos characteristics analysis and intelligent prediction study of roc-kburst based on monitoring time-series[D].Xuzhou:China University of Mining and Technology,2013. [16] 董陇军,李夕兵,白云飞.急倾斜煤层顶煤可放性分类预测的Fisher判别分析模型及应用[J].煤炭学报,2009,34(1):58-63. Dong Longjun,Li Xibing,Bai Yunfei.A Fisher discriminant analysis model for classifying of roof coal cave-ability of steep seam[J].Journal of China Coal Society,2009,34(1):58-63. [17] 钟 冲,郭 强.费歇尔判别法及其应用[J].西南交通大学学报,2008,43(1):136-141. Zhong Chong,Guo Qiang.Fisher discrimination method and its application[J].Journal of Southwest Jiaotong University,2008,43(1):136-141. [18] 付玉华,王兴明.岩体质量分级的 Fisher 判别分析模型及应用[J].金属矿山,2012(12):107-110. FuYuhua,Wang Xingming.Study and application of fisher discriminant analysis model to classification of rock mass quality[J].Metal Mine,2012(12):107-110. (责任编辑 徐志宏) Prediction on Classification of Rock Burst Hazard Based on Fisher Discriminant Analysis Shao Liangshan Xu Bo(SystemEngineeringInstitute,LiaoningTechnicalUniversity,Huludao125000,China) In view of the issues of rock-burst hazard classification in the mine,the factor analysis and Fisher discriminant analysis theory are applied to select coal thickness,coal seam dip angle,buried depth,structure condition,dip angle of coal seam,coal seam thickness changes and the gas concentration,the roof management,unloading,ring of coal guns as influence factors.Through the analysis of the correlation between the influencing factors,the appropriate public factors are extracted from the factors with strong correlation with the application of factor analysis.The Fisher discriminant analysis(FDA) model based on factor analysis is built to predict the rock-burst hazard rating.23 sets of measured data from Sichuan Yanshitai Mine are used as samples to make training.Then,the backward substitution method was adopted to verify the effectiveness of the model,with the misjudgment rate of 0.With another 12 groups of measured coal mine dynamic phenomena data that are not trained as cases,their hazard classification are predicted and compared with that obtained by the traditional Fisher discriminant method.The results show that the sample index number decreases and the correlation reduced by the factor analysis.It can effectively predict the level of rock burst hazards,and the prediction misjudgment rate is zero through this model. Rock burst,Prediction,Classification,Factor analysis,Fisher discriminant analysis,Re-substitution method 2014-11-04 国家自然科学基金项目(编号:71371091),辽宁省科学研究计划项目(编号:2010230004)。 邵良杉(1961—),男,博士,教授,副校长,博士生导师。 X936 A 1001-1250(2015)-01-138-07


2 冲击地压危险性等级预测的FDA模型







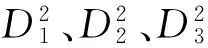

3 结 论

