应力扰动对地震周期和地震矩影响的数值模拟

翁辉辉 黄金水

1） 中国合肥230026中国科学技术大学地球和空间科学学院地震和地球内部物理实验室2） 中国合肥230026蒙城地球物理国家野外科学观测研究站



应力扰动对地震周期和地震矩影响的数值模拟

1） 中国合肥230026中国科学技术大学地球和空间科学学院地震和地球内部物理实验室2） 中国合肥230026蒙城地球物理国家野外科学观测研究站

利用二维有限元数值模型， 结合断层滑移弱化摩擦准则对断层滑动规律以及应力扰动对其影响进行了研究． 数值计算结果表明， 在均匀应力分布情况下, 平面断层滑动显示出典型的特征地震规律， 断层面上的应力扰动对断层滑动规律产生影响， 压应力增加明显延迟地震的发生时间， 并增加地震释放的能量． 应力扰动发生在地震破裂临界区时的影响比在震前滑移区时的影响显著． 当发生在地震滑移区时， 若应力扰动足够大， 则压应力增大会造成地震发生时部分动力断层被暂时锁住， 使得地震释放的能量变小， 但可增加后续地震的能量； 而压应力减小则可导致地震规律产生更加复杂的变化， 会即时触发地震． 如果应力扰动发生在一个地震周期的早期， 则触发的地震较小， 但可导致随后的地震提前发生； 如果应力扰动发生在一个地震周期的后期， 则会触发大地震． 当应力扰动位于震前滑移区或破裂临界区时， 小的扰动也可能产生类似的效果． 应力扰动产生越晚， 这种影响也越明显． 应力扰动发生在破裂临界区的影响最明显． 应力扰动的影响一般主要集中在应力发生扰动后的1—2个地震周期内． 后续地震基本恢复无应力扰动时的特征地震规律．

特征地震 有限元数值模拟 滑移弱化摩擦准则 应力扰动

引言

20世纪初， 尽管当时还没有认识到板块构造运动， 但地震学家就已经认识到地震是地壳应力的突然释放所造成的（Reid, 1910）． 这种认识后来发展为弹性回跳理论， 即断层两边岩石在构造应力的作用下发生形变， 应力和应变能逐渐累积， 当应力达到一定程度就会造成断层的突然活动， 从而导致地震发生， 应变能也得到突然释放． 目前该理论被认为是构造地震发生的主要机制（Shearer, 2009）． 现代空间大地测量技术可精密测定地震前的缓慢应变累积过程和地震时的突然形变（同震位移）（Fialko, 2006; Rueggetal, 2009; 武艳强等, 2013; Diaoetal, 2013; Karimzadehetal, 2013）． 野外地质调查和岩石物理实验表明， 地震的这种过程可以简化为断层的黏滑行为（Robinsonetal, 2010）． 而且断层的这种黏滑可以用滑移弱化摩擦准则（Duan, 2012）或一个与速率和状态相关的摩擦准则（Scholz, 1998） 来表示．

基于摩擦准则的弹性回跳理论模型的一个隐含前提是， 近乎相同大小的地震会在一个地方有规律地重复发生， 即所谓的特征地震（Schwartz, Coppersmith, 1984; Igarashietal, 2003）． 尽管有关特征地震的认识到目前仍存在很大的争议（Wesnousky, 1994; Jackson, Kagan, 2006）， 但许多观测资料， 特别是历史地震资料显示（Fedotov, 1965; Sieh, 1978; Swanetal, 1980; Elliottetal, 2009; Robinsonetal, 2010）， 大地震的确会在一个地方重复发生， 许多小地震也显现出重复发生的规律（Nadeau, McEvilly, 1999; Igarashietal, 2003）． 一个最典型的案例是美国加利福尼亚圣安德烈斯断层帕克菲尔德区域所发生的一系列地震． 该断层在1857， 1881， 1901， 1922， 1934和1966年共发生6次M6.0左右的地震， 平均每22年就会发生一次M6.0左右的大地震 （Bakun, McEvilly, 1984; Bakun, Lindh, 1985）． 尽管据此预报的地震没有准时发生， 但还是在同一地点于2004年发生了一次M6.0地震（Bakun, Lindh, 1985; Bakunetal, 2005）．

帕克菲尔德地震没能按照预测的那样按时发生， 一个普遍的认识就是该区的应力场可能受到附近地震的影响． 例如, 一种解释是1983年5月2日发生于加州科林佳（Coalinga）的MW6.4地震可能缓解了帕克菲尔德地区的应力（Simpsonetal, 1988）， 另一种解释是1906年旧金山大地震后应力的松弛效应推迟了帕克菲尔德地震的发生（Ben-Zionetal, 1993）． 显然， 附近应力场变化会影响地震发生的规律， 增加地震预测的难度． 要提高这方面的认识， 需从物理上认识应力场变化对地震发生规律的影响．

目前利用物理模型进行的地震预测仍然面临很大困难， 但基于物理模型提高对地震发生规律的认识取得了长足的进步（Stuart, 1988; Scholz, 1998; Kato, Tullis, 2001）． 利用一定的摩擦准则研究断层破裂或活动规律， 已可在一定程度上计算模拟地震的孕育、 发生和发展规律（蔡永恩等, 1999; Kato, Hirasawa, 1999; Caietal, 2000; Kato, 2003; 朱守彪等, 2008; 朱守彪, 张培震, 2009）． 有些结果与已有的观测呈现出很好的一致性（朱守彪等, 2008）． 这些研究为我们进一步认识地震发生的规律提供了物理参考模型．

帕克菲尔德地震的预测试验表明特征地震规律可能仍然存在， 只是这种规律可能受周围应力场变化的影响． 本文目的就是试图在前人开展的物理模型研究的基础上， 采用有限元数值模拟的方法来了解应力变化对地震发生规律的影响． 为了探讨应力变化的影响， 我们建立了一个非常简单的特征地震模型， 然后通过改变应力场探讨应力变化时特征地震的变化规律． 本文首先介绍有关有限元数值模拟方法， 然后给出一个均匀背景应力场下的基于滑移弱化摩擦准则的特征地震参考模型， 并给出该模型的地震发生规律， 最后讨论应力变化导致断层面上不同区域应力扰动对特征地震发生规律的影响， 为认识了解应力变化对地震发生规律的影响提供参考数值模型．

1 模型设置与模型参数

为探讨应力变化对地震发生规律的影响， 我们首先需要建立基于摩擦准则的断层黏滑模型． 由于有限元计算中给出的精确应力分布需要很高的分辨率， 该模型采用一个较小范围的二维10 km×20 km弹性模型． 弹性介质的密度、 剪切模量和泊松比分别为2.7 kg/m3, 28 GPa和0.25． 模型的左右两侧为自由滑移边界条件， 上下两侧为自由边界条件． 断层从中间穿过（图1a）， 且分别为具有不同特性的两段： 一段是无震断层， 即断层持续滑动， 其长度为6 km， 下面称之为运动断层， 以10 cm/a的相对速度发生滑动； 另一段称为动力断层， 其长度为4 km（图1a）， 由摩擦准则约束， 根据应力变化可处于闭锁状态或产生滑动．

动力断层的滑移弱化摩擦准则表示为

（1）

式中，μs和μd分别为静摩擦系数和动摩擦系数，d0为滑移弱化距离，d为断层累积滑移距离． 需要说明的是， 滑移弱化距离对断层的摩擦行为具有很重要的影响， 这种影响对研究断层的破裂动力学过程非常重要． 研究表明， 在滑移弱化准则下， 断层破裂成核的特征长度与滑移弱化距离d0成正比（Uenishi, Rice, 2003）． 正因为如此， 滑移弱化距离对模型的地震大小和复发周期也起到非常重要的作用． 减小特征滑动距离会减小地震的周期和大小． 但在我们的模型中， 由于忽略地震的破裂过程， 其影响主要表现在对地震的周期和大小上． 有关滑移弱化距离的影响详见Uenishi和Rice（2003）文章． 因此本文模型的周期与大小除了与本文模型参数相关外， 与本文设置的滑移弱化距离也密切相关. 我们将滑移弱化距离d0设置为2 m， 这与Duan（2012）计算中采用的1.5 m的数值接近． 另外需要指出的是， 由于滑移弱化距离影响成核特征长度， 而如果成核特征长度很小， 就需要很高的模型空间分辨率， 从而极大增加计算时间． 为了控制模型计算量和保证空间分辨率， 我们选取的滑移弱化距离略微偏大． 累积滑动距离d是对一次地震破裂过程而言的， 因而仅在判断地震滑动时起作用， 每次断层滑动之后均恢复为0．

图1 （a） 二维有限单元网格， 白色线段表示动力断层， 黑色线段表示右旋走滑运动断层； （b） 动力断层摩擦系数分布， 虚线为静摩擦系数， 实线为动摩擦系数； （c） 动力断层初始应力， 虚线为正应力， 实线为切应力， 六角星表示施加应力扰动的位置

为使动力断层与运动断层连接不产生大的应力奇异分布， 本模型中将动力断层靠近运动断层的一小段作了滑移强化处理， 即取μs<μd， 从而让断层稳定滑动． 同时也在动力断层的孕震段（即μs>μd）设置了一个摩擦系数过渡区域（图1b）． 岩石摩擦系数的变化范围很大（Byerlee, 1978; Tsutsumietal, 2011）， 这里模型的静摩擦系数与动摩擦系数分别设为0.6和0.4， 强化段断层长度约为1 km, 动摩擦系数为0.601（图1b）． 断层围岩应力场及其变化通过在断层面施加应力的方法来实现（Aagaardetal, 2013）． 岩石圈的应力状态变化很大（Townend, Zoback, 2004）， 由于围岩作用在断层上的切应力可以通过线性叠加的方式直接在断层切应力的计算中予以考虑， 这里的模型仅考虑围岩正应力的影响． 为简单起见， 围岩正应力设为恒定值-200 MPa（负的正应力代表压应力）． 应力变化通过在断层的不同位置增加正应力扰动来实现． 为使模型的第一发震周期与后续一致， 我们在模型的动力断层中设置了初始切应力， 其大小为动摩擦系数乘以正应力（图1c）． 注意到强化断层的初始切应力已经达到最大静摩擦力， 因此强化断层将一直处于滑动中．

断层上的摩擦力τf由下式计算:

（2）

式中，σ为正应力，μ为式（1）表示的摩擦系数． 断层滑动由下式控制：

Δτ=|τ|-τf,

（3）

式中，Δτ为切应力差，τ为断层上的切应力，τf为断层上的摩擦力. 当Δτ<0时， 动力断层两侧则保持黏着不动； 当Δτ>0时， 动力断层两侧将发生滑动， 滑动方向由τ的方向确定． 本文数值模拟计算中忽略断层的破裂细节， 对断层上的应力和滑移在每一时间步按下述方法处理：

1） 在每一步的开始， 首先假设动力断层上的滑移量为0， 根据边界条件和运动断层的位移状况计算模型的应力分布；

2） 根据式（1）、 （2）计算动力断层节点的摩擦力， 然后通过式（3）判别动力断层上的切应力差Δτ；

3） 如果每一个节点Δτ<0, 可进行下一步计算； 如果有节点Δτ>0, 则根据应力应变关系， 利用Δτ计算这些节点滑移量， 并将该滑移量赋于这些节点；

4） 根据上述计算得到动力断层上的滑移量， 结合边界条件和运动断层的位移状况重新解算系统的应力应变分布， 并给出动力断层上新的应力分布；

5） 重复步骤2）—4）， 直到动力断层上所有节点的切应力都不大于断层摩擦力， 则此时所有断层节点停止滑移． 这一时间步所得到的滑移量即地震同震位移．

在动力断层的切应力无法克服摩擦滑动时， 根据步骤1）—3）计算模型应力应变随时间的变化. 当动力断层上的切应力足够大， 可以导致断层滑动时， 通过步骤2）—5）的迭代， 计算断层的滑移分布．

利用同震滑移分布可以计算地震大小． 地震矩定义为

M0=μSA，

（4）

式中，μ为剪切模量，S为断层破裂面积，A为断层平均滑移距离． 在本文的二维模型中， 计算时采用断层破裂长度来表示断层的破裂面积． 应该指出的是， 本文模型的断层参数与实际参数相差甚远， 模型地震矩与实际地震矩会相差很大， 仅为描述地震相对大小用．

对地震发生过程的分析， 我们最关心的是应力变化． 断层面上的应力变化按常规采用库仑应力表示， 其定义为

ΔC=|Δτ|+μsΔσ，

（5）

式中，Δτ为断层上点的切应力变化， Δσ为断层上点的正应力变化． 由模型的静摩擦系数（0.6）和动摩擦系数（0.4）以及断层面上初始正应力（-200 MPa）和切应力（-80 MPa）可知， 如果ΔC达到 40 MPa， 则断层上的相应点将产生滑动． 因此该模型库仑应力的临界值就是40 MPa．

本模型计算采用有限元方法， 网格采用从边界向断层区域逐渐加密的三角形网格（图1a）， 断层处分辨率最大， 最小网格边长为50 m． 计算时间步设为0.5年． 断层处的不连续性用关联网格来实现， 即对每一个断层节点， 改变其拓扑结构， 增加自有度， 相当于将该节点划分为两个， 分别归属于左右两边的网格， 同时在中间增加虚拟节点， 并与上（下）同样增加的中间虚拟节点组成矩形关联网格单元． 关联网格单元没有体积， 用来实现断层两边的滑动． 有限元模型采用PyLith程序解算（Aagaardetal, 2013）．

2 数值结果

2.1 均匀背景应力场模型的地震发生规律

为了解应力场变化的影响， 我们首先给出均匀背景应力场下断层的滑动规律． 开始时， 断层及其周边的应力场变化为0， 断层面上的库仑应力为0， 动力断层将处于闭锁状态． 当运动断层开始活动， 由于动力断层仍处于闭锁， 断层及其附近区域的应力场将发生变化． 应力张量的分量及动力断层面上的正应力和切应力的变化如图2所示． 应力张量分量的变化形态（图2a--c）在不同时间仅幅值发生变化． 随着运动断层的进一步运动， 在x方向逐渐增加动力断层右侧的张应力和左侧的压应力（图2c）； 在y方向， 由于运动断层导致动力断层产生一个顺时针方向的旋转趋势， 在断层附近产生梅花瓣型的应力分布（图2a）； 动力断层上的切应力不断增大（图2b）． 当动力断层上切应力在部分区域达到-120 MPa（图2b， d）时， 断层产生滑动． 当滑动停止时， 动力断层的摩擦力将处于静摩擦状态． 此时应力场恢复到初始应力状态． 随着运动断层的进一步运动， 下一个周期开始． 需注意到， 动力断层面上正应力变化很小（图2a， c和e）． 图2d， e显示了3个地震滑动周期中动力断层面上的正应力与切应力的变化过程．

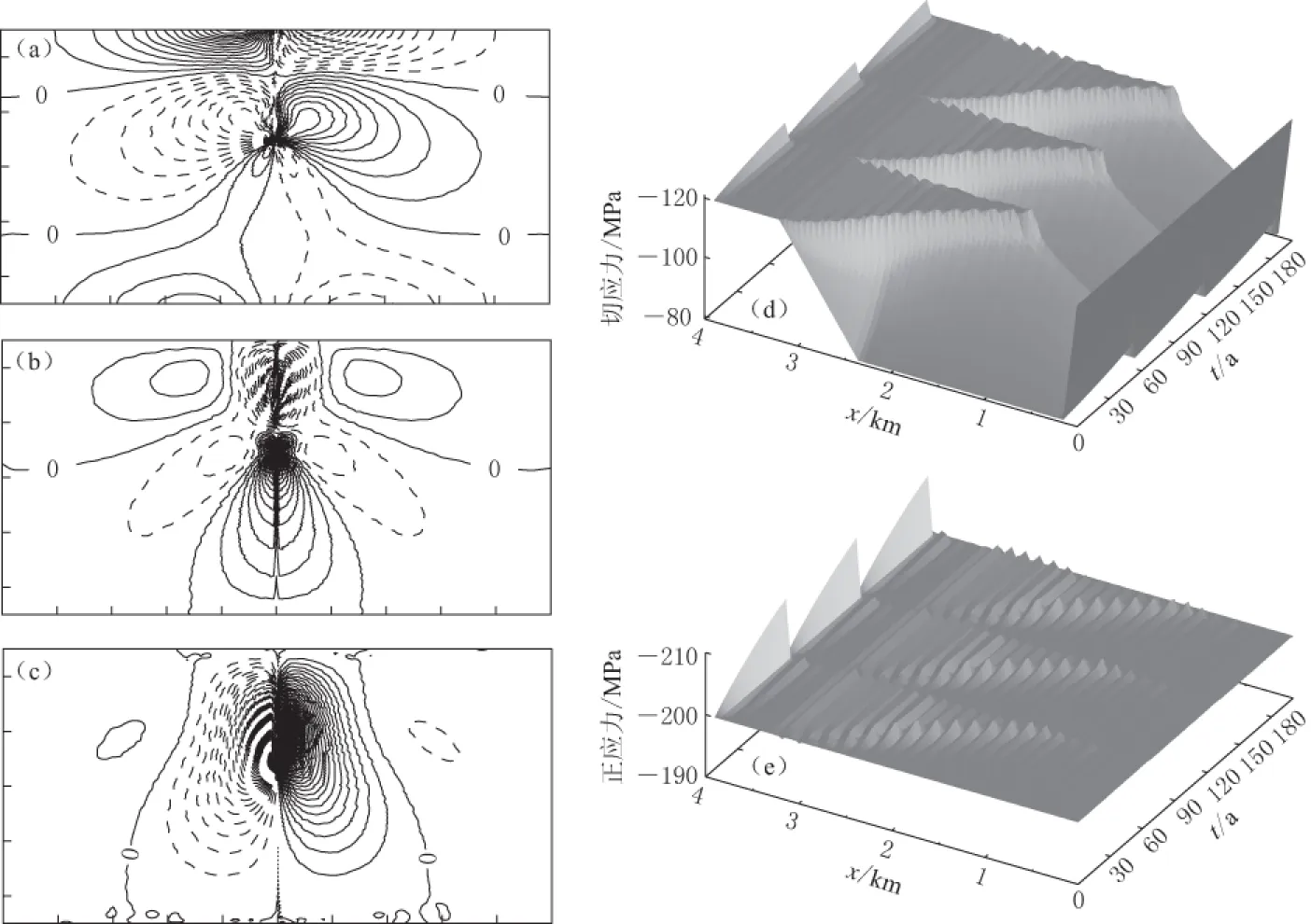
图2 模型在断层滑动前一时间步的平面应力变化（a, b, c）以及动力断层上的切应力（d）和正应力（e）的时空变化． 图（a）、 （b）和（c）分别表示应力张量的yy， xy和xx分量. 拉张正应力和左旋切应力为正， 以实线等值线表示； 压应力和右旋切应力为负， 以虚线等值线表示． 等值线间隔为2 MPa， 图中标出了0值等值线

图3给出了x=1 km处垂直于断层的直线上的x方向位移（图3a）、 动力断层（包括强化断层）的位移（图3b）和动力断层但不包括强化断层的库仑应力变化情况（图3c）． 从图3a可以看到， 一次地震的同震位移接近7 m， 对一个4 km的断层而言显得偏大， 这既与我们选取的模型参数有关， 也与前面提到的滑移弱化距离的选取偏大有关． 同时值得注意的是， 在动力断层处于闭锁状态时， 模型的位移场不会完全对称． 但垂直断层两边直线上的位移相对其与断层交点基本对称（图3a）． 因此图3a中显示的位移都是相对于该交点的相对位移． 图3a清楚地显示了弹性回跳模型的位移变化情况： 在动力断层处于闭锁状态时， 运动断层的持续运动造成动力断层两边位移持续增大， 在断层附近产生大形变； 当地震发生时， 断层发生错动， 同震形变主要发生在断层附近（图3a）． 从图3b中可以看到， 尽管大约x=3 km至x=4 km处的强化断层一直在滑动， 但由于闭锁段断层的影响， 强化断层上的位移并不均匀． 但当运动断层位移达到足够大时， 整个动力断层发生滑动， 由于模型参数均匀， 断层各点在断层滑动后位移都相同（图3b）． 从图3b中还可以看到， 闭锁段（x<2.4 km）各点并不同时滑动， 而是靠近运动断层端的有些点先开始滑动． 这从该段的库仑应力分布上（图3c）也可以看出． 由于靠近运动断层， 这些点的库仑应力先达到滑移设定的临界值， 从而先开始运动， 但整个模型集聚的应变能并不足够使整个断层破裂． 当大约有一半的点（约在x=1.2 km处）达到库仑应力临界值时， 整个断层才开始破裂滑移， 尽管这时仍有一半的点未达到库仑应力临界值（图3c）． 为后面表述方便， 我们将库仑应力未达到临界值就产生滑移的区域称为地震破裂区， 将整个断层产生滑移前库仑应力就已经达到临界值并已经产生滑移的区域称为震前滑移区， 而将两个区域交接处称为地震破裂临界区．

图3 （a） x=1 km处水平测线在x方向上的位移和同震位移分布, 点线代表起始的位移分布， 从细到粗的实线分别表示20， 66和66.5年的位移分布， 虚线代表测线上的同震位移； （b） 模型动力断层在不同时间的位移， 每条曲线代表不同时间的位移值， 曲线时间间隔为0.5年， 黑色实线表示地震前一时间步的位移； （c） 模型动力断层面库仑应力变化图， 从细到粗的实曲线分别代表10， 30， 40， 50， 66和66.5年的库仑应力曲线， 虚线为临界库仑应力值

在本文的模型中， 断层每次滑动前积聚的应变能都得到完全释放， 因而得到很好的地震重复发生的规律（图2d， c和图3b）． 模型的地震发生周期为66±1年（前3个地震周期序列分别为66.5， 65.5和66.5年）， 每次地震释放的能量为（5.79±0.06）×1011N·m（前3个地震矩分别为5.79×1011， 5.73×1011和5.79 ×1011N·m）． 这里计算的能量不包括地震发生前有部分点已经发生滑动所释放的能量． 该模型是典型的 “特征地震”模型（Brace, Byerlee, 1966）．

2.2 应力扰动对模型地震规律的影响

探讨应力扰动的影响是一个非常复杂的问题． 首先是应力扰动的大小， 若应力扰动很小， 可能不会产生任何影响； 其次是应力扰动发生的时间， 即使很大的应力扰动， 在一个地震周期早期， 其影响肯定与临震时产生的影响不同； 另外， 应力扰动的位置以及应力扰动是增加摩擦力还是减小摩擦力也是重要的影响因素． 为将复杂问题简单化， 本文设计了两组共36个算例， 一组探讨增加摩擦力的影响， 另一组探讨减小摩擦力的影响． 每组又分别包含两个不同的应力扰动大小的算例， 应力扰动大小分别设为背景正应力的80%和20%， 即160 MPa和40 MPa． 正应力扰动添加的位置分别设于x=150， 1250和2050 m处（图1c）， 这3个位置分别对应地震破裂区、 地震破裂临界区和震前滑移区， 应力扰动作用在断层面的长度均设为300 m． 由于本模型特征地震的周期为66年， 应力扰动添加的时间分别放在20， 40和60年． 下面将详细介绍模型的计算结果.

1） 断层面上压应力增加的影响. 由式（5）可看出， 压应力增加的位置上其库仑应力减小， 从而使这些点难以达到库仑应力临界值而滑动， 进而延迟地震发生的时间． 另一方面， 由于压应力增加， 使摩擦力增大， 根据式（2）和（3）， 断层将更难以滑动， 或者说， 需要积累更多的能量使断层滑动． 这种影响可能导致地震发生时所释放的能量更大． 但是从计算结果看， 情况远比这复杂． 表1给出了18种不同情况下应力扰动对发震周期和地震矩影响的结果．

表1 压应力增加的应力扰动模型的地震周期与地震矩序列Table 1 Earthquake cycles and seismic moments of models with increased pressure on the fault

*添加应力扰动的时间与改变应力扰动的相对大小

应力扰动发生的位置对地震规律可产生显著影响． 当应力扰动发生在震前滑移区时， 由于该区的滑移条件是切应力需达到库仑应力滑移临界值， 所以压应力扰动将导致该区切应力难以达到库仑应力临界值而延迟地震发生的时间． 从图4a可以看出， 应力扰动减小了

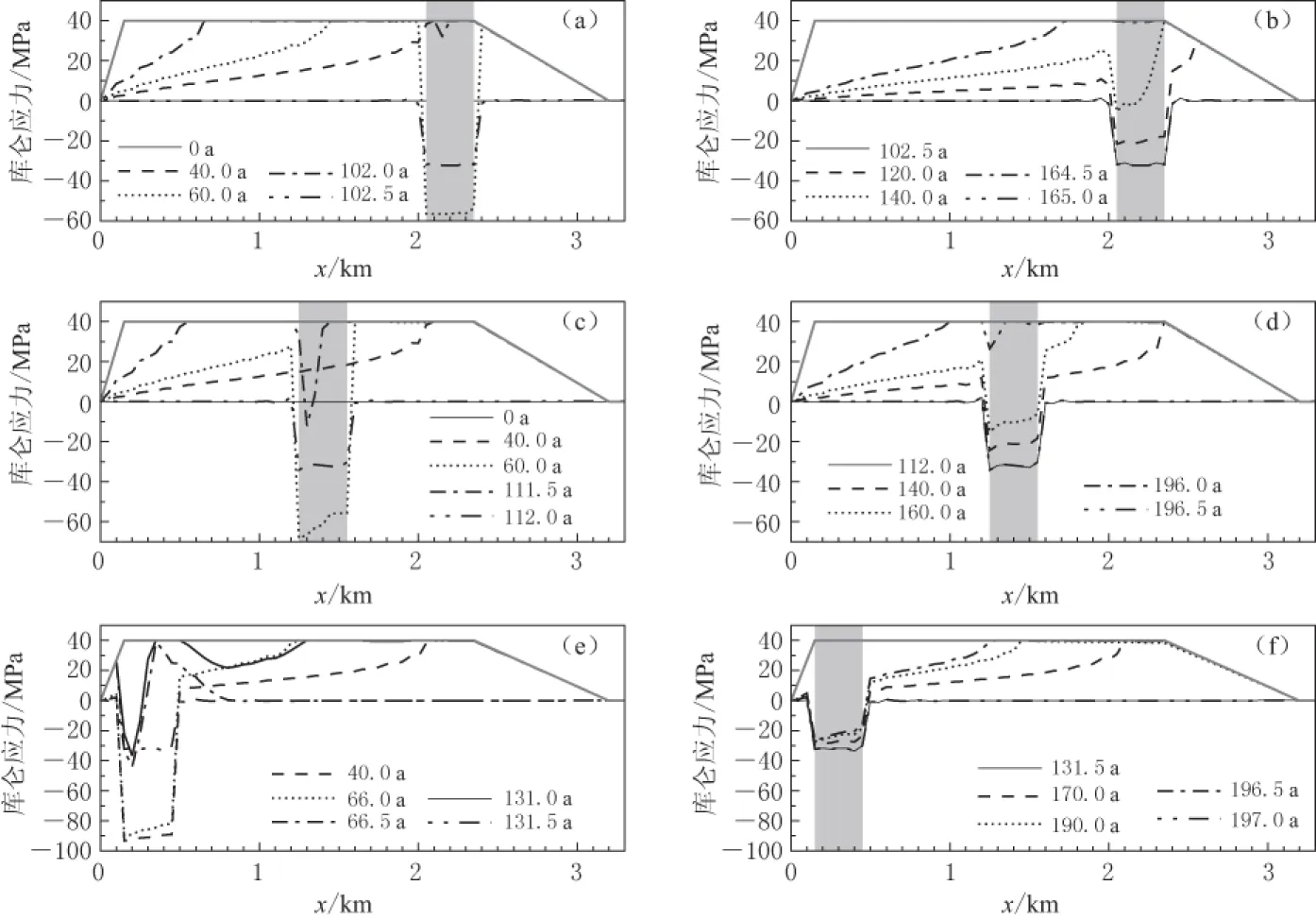
图4 60年时在震前滑移区压应力增加80%的动力断层库仑应力分布图（a, b）, 60年时在破裂临界区压应力增加80%的动力断层库仑应力分布图（c, d）以及40年时在地震滑移区压应力增加80%的动力断层库仑应力分布图（e, f）． 灰色部分表示应力扰动区， 灰实线表示临界库仑应力值， 其它线条分别代表不同时间断层面上的库仑应力分布

该区库仑应力值， 然后随时间增加， 该区库仑应力逐渐增加． 这一过程明显延迟了地震的发生时间（表1， 图5a）， 时间的加长意味着能量积累得更多， 因而地震释放的能量相应地增加（表1 ）． 但是， 这种应力扰动只对扰动加入的这个地震周期产生这种显著影响． 第一次地震发生后， 震前滑移区应力扰动区的切应力已经得到部分加载和保持， 切应力增加导致的库仑应力增加部分抵消了正应力增加导致的库仑应力减小， 在破裂临界区的库仑应力达到临界值时， 正应力扰动区的库仑应力也达到临界值（图4b）， 因而应力扰动对此后的地震序列影响很小， 此后的地震序列基本恢复至原来的特征地震序列（图4b和图5a）． 但应该注意到, 新的特征地震序列与均匀参考模型的特征地震序列略有不同， 如其地震周期为62—63年， 比参考模型的周期66年略小一些． 这是由于震前滑移区的应力扰动增加了滑动所需切应力， 从而改变了破裂传导的速度， 使得震前滑移区变小． 对比图4b与图3c可以发现， 震前滑移区应力扰动模型的震前滑动区大约对应在x>1.7 km， 均匀参考模型的相应区域为x>1.2 km． 这种效应略微减小了后续特征地震的周期， 也相应略微减小了地震矩（表1）． 应力扰动加入时间总体对发震规律影响不大， 但越临近地震发生， 对应力扰动发生后的第一次地震的延时效应越明显， 同时也增加了地震的震级（表1， 图5b）． 若减小应力扰动值的大小， 而不改变上述变化规律， 则可显著改变其影响规模（表1， 图5c）． 当应力扰动仅为原有值的20%时， 地震周期和地震矩基本接近原均匀模型特征地震的规律．

图5 20年时在震前滑移区压应力增加80%的滑移时空分布（a）, 60年时在震前滑移区压应力增加80%（b）和20%（c）的滑移时空分布, 40年时在破裂临界区压应力增加80%（d）和正应力增加20%（e）的滑移时空分布以及40年时在地震滑移区压应力增加80%的滑移时空分布（f）.图中虚线为加入应力扰动时刻的滑移时空分布

当应力扰动发生在地震破裂临界区时， 其影响与发生在震前滑移区时存在显著区别（表1， 图4a--d）． 首先， 对第一次地震的影响显著增强， 应力扰动加入的时间则影响不大. 随着应力扰动数值减小， 影响也相应减小（表1； 图4a， c； 图5a， d， e）． 应力扰动在地震破裂临界区的影响比在震前滑移区的影响效果更为显著， 这是因为如果没有该区应力扰动的影响， 断层基本积累滑动所需要的能量， 但当该区产生应力扰动后， 必须增加足够的应力以克服该区由于正应力增加而增加的摩擦力. 而当应力扰动位于震前滑移区时， 扰动区应力的增加可与地震破裂临界区应力的增加同步进行， 从而受到的影响要小（图4a， c； 图5a， d）． 其次， 应力扰动发生在地震破裂临界区时对随后的特征地震仍存在很大影响（表1； 图4b， d； 图5a， d）， 后面特征地震的周期仍然比均匀参考模型长， 特征地震的地震矩仍然比均匀参考模型大， 但总体来说， 应力扰动对后续地震的影响比第一次的要小， 这与应力扰动发生在震前滑移区时的道理相同． 对应力扰动加入的时间影响不大， 随着应力扰动数值减小， 影响也相应减小（表1； 图5d， e）．

当应力扰动发生在地震滑移区时， 对地震周期和地震矩来说， 总体影响不大（表1）． 但值得注意的是， 当应力扰动足够大时（如80%的扰动量）， 扰动增加时首次地震断层破裂无法通过该区， 使得第一次地震很小（表1； 图4c， f； 图5f）． 这种影响对后续地震序列也会产生影响． 由于后续的第二次地震能破裂整个断层， 在地震滑移区产生更大的滑移量， 因而随后的第二次地震一般要大（表1， 图5f）． 应力扰动加入时间影响不大， 但当应力扰动很小（如20%的扰动量）时， 将不会造成首次地震时部分断层被锁住的情况， 因而几乎无影响（表1）．

2） 断层面上压应力减小的影响. 与前面讨论断层面上压应力增加的影响一样， 本文也计算了18个断层面上压应力减小的影响的模型（表2）． 总体来说， 根据式（5）计算表明， 减小压应力的位置， 其库仑应力增加， 从而使这些点易于达到库仑应力临界值而滑动， 进而使地震发生的时间提前． 另一方面， 由于压应力减小， 使摩擦力减小， 根据式（2）、 （3）可看出， 断层将更易于滑动， 或者说， 不需要积累太多的能量即可使断层滑动． 这种影响可能导致地震发生时释放的能量减小． 但具体情况与压应力增加的模型相比更加复杂（表2）．

表2 压应力减小的应力扰动模型的地震周期与地震矩序列Table 2 Earthquake cycles and seismic moments of models with decreased pressure on the fault

*添加应力扰动的时间与改变应力扰动的相对大小

压应力减小的模型的一个重要特征是， 当应力扰动足够大（如80%的扰动量）时， 应力扰动的加入会即时触发断层活动， 即产生地震． 只是触发的地震矩由于触发的时间和位置不同而不同． 同时， 当触发大地震时， 后续地震基本具有特征地震的规律； 但当触发一次小地震时， 随后的大地震会提前发生， 然后基本恢复特征地震的规律（表2）．

断层发生位移， 需要库仑应力达到临界值． 一般而言在一个地震周期早期（如20年）， 其断层面上库仑应力变化较小. 当断层面上发生应力变化， 而应力扰动足够大时， 局部库仑应力达到临界值， 该区就会产生滑动， 从而产生地震（图6a， b）． 但早期的应力扰动和随之触发的断层小滑动不足以显著改变断层的库仑应力分布， 从而无法触发大地震的发生． 从图6a中可以看出， 震前滑移区的库仑应力在应力扰动加入前， 大约达到库仑应力临界值的30%， 但加入80%的应力扰动后， 该扰动区库仑应力就达到临界值， 该区域产生滑移（图6b）， 即产生小震． 如果应力扰动很小（如20%的扰动量）， 则不会产生滑移， 从而就不会触发小地震（表2）． 应力扰动加入的位置对这种规律影响很小．

当应力扰动加入在一个地震周期的晚期（如60年）， 由于临震滑移区的库仑应力大多已达到临界值， 一个大的应力扰动（如80%的扰动量）所导致的库仑应力变化就足以使整个断层滑动， 因而导致大地震的发生（表2； 图6c， d）； 一个小的扰动（如20%的扰动量）发生在地震滑移区时， 则影响很小． 这是因为， 一般在地震滑移区的库仑应力在震前都不超过50%， 所以小的应力扰动不会导致断层产生小滑移， 对整个断层库仑应力的影响也非常有限． 但当小的应力扰动发生在震前滑移区和破裂临界区时， 其在地震周期晚期的作用就很大， 亦即小的应力扰动的加入也能触发大地震（表2； 图6e， f）．

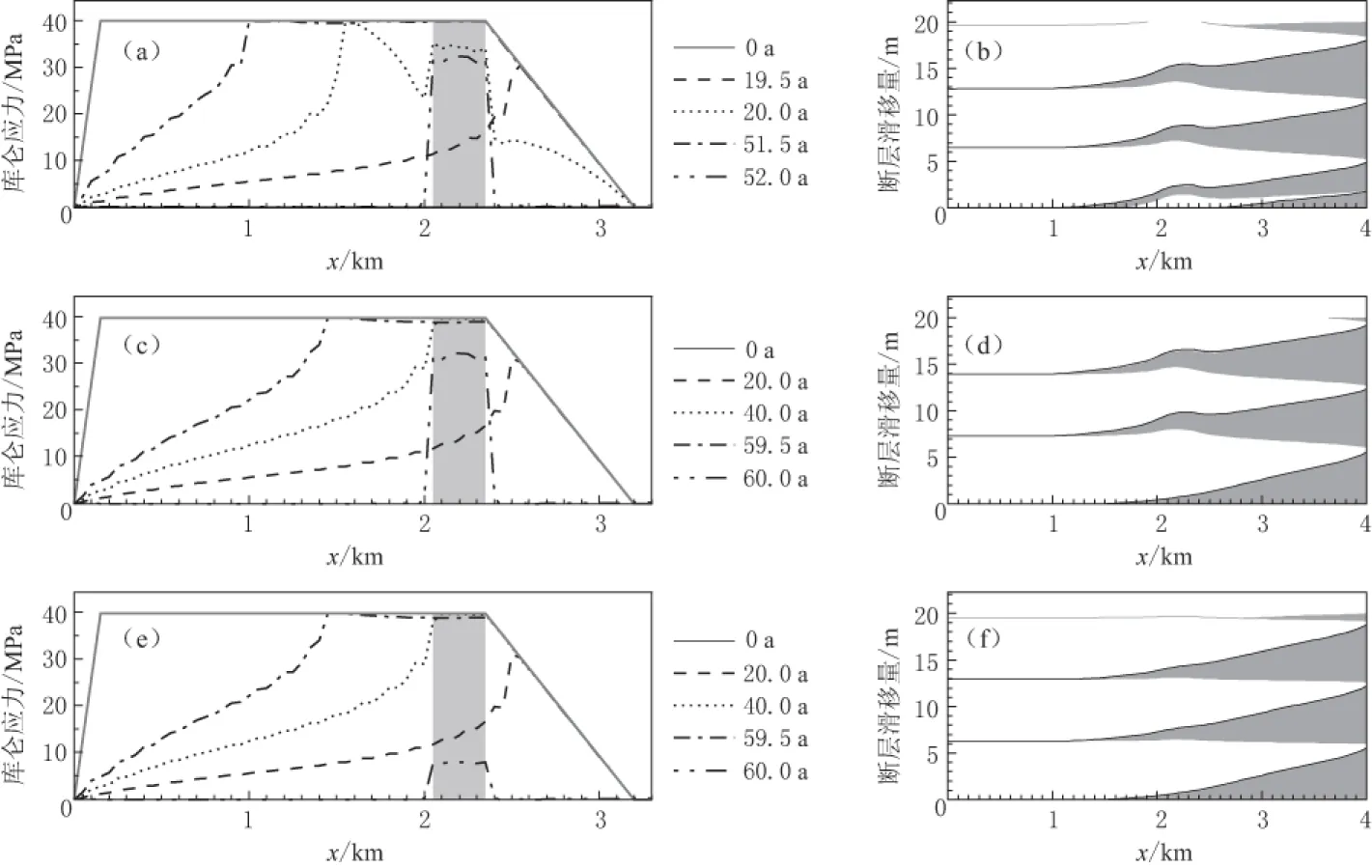
图6 动力断层库仑应力分布图（a, c, e）及滑移时空分布图（b, d, f）． 分别为20年时在震前滑移区压应力减小80%（a, b）， 60年时在震前滑移区压应力减小80%（c, d）和60年时在震前滑移区压应力减小20%（e, f）的模型

应力扰动加入时间和位置的影响具有一定的耦合效应， 其在震前滑移区和破裂临界区的影响大于地震滑移区， 地震周期后期的影响大于前期． 若在一个地震周期中期（如40年）加入应力扰动， 当扰动很大（如80%的扰动量）时， 震前滑移区和临震破裂区会导致大地震的发生， 而在地震滑移区则只会产生小地震； 当扰动较小（如20%的扰动量）时， 震前滑移区只会导致小地震的发生， 在临震破裂区和地震滑移区对地震序列影响则很小（表2）.

值得注意的是， 小震的发生一般均会导致后续大地震的提前发生（表2）． 从图6a和图6c中可以清楚地看到这种影响． 图6c的应力扰动是在60年时加入的， 所以图中20年时的库仑应力曲线显示没有受到扰动影响. 图6a显示在20年时加入应力扰动后， 断层面上库仑应力值发生显著变化， 极大地增大了断层面上震前滑移区和破裂临界区的库仑应力值， 因而使得后续地震提前发生． 除此之外， 早期（如20年）发生在震前滑移区和破裂临界区的小的应力扰动也增加了区域的库仑应力值， 但是其库仑应力值还未达到临界值， 因此并不能触发断层滑移． 尽管如此， 它们也会导致后续大地震的提前发生， 只不过其影响效果比小震更小（表2）. 其中发生在破裂临界区的影响更为显著， 与触发小震的模型类似， 影响之后的地震也基本恢复特征地震规律．

另一个值得注意的现象是， 当应力扰动加在震前滑移区时， 无论是引发小震还是大地震， 因为促使地震提前发生， 应变能累积就少， 所以后续地震矩相对较小； 当应力扰动发生在破裂临界区时， 这种影响更加明显， 由于加入的应力扰动一直存在影响， 所以这种情况下后续特征地震的规律也略微发生改变， 即周期变小、 震级减小（表2）； 而当应力扰动发生在地震滑移区时， 由于地震破裂在应力扰动减小库仑应力时将更容易滑动， 从而产生更大的同震位移， 使得触发的大地震或触发小地震后的大地震的震级都明显增大（表2）．

3 讨论与结论

本文利用一个简单的走滑断层模型及滑移弱化摩擦准则， 采用二维有限元数值模拟的方法研究了断层滑动规律以及断层面正应力变化对地震规律的影响． 均匀应力分布断层模型显示出典型的特征地震规律， 地震复发周期约为66年， 地震矩约为5.79×1011N·m． 断层滑动可划分出3个典型的滑移区域： 地震滑移区、 破裂临界区和震前滑移区． 断层在发生大规模滑动前， 地震滑移主要发生在震前滑移区， 随着时间推移， 地震滑移区不断扩大， 当滑动区达到一定程度（即地震滑移区到达地震破裂临界区）， 就造成了闭锁的地震滑移区发生滑动． 大量数值模拟计算显示， 不同时间在断层不同位置发生的应力扰动对地震规律产生不同影响， 极大地改变原特征地震的发生规律． 其具体表现为：

1） 断层面上压应力增加的影响根据应力扰动的位置不同而不同． 当变化发生在震前滑移区和地震破裂临界区时， 压应力增加明显地延迟了地震发生时间， 并相应地增加了地震释放的能量． 发生在地震破裂临界区时的影响比发生在震前滑移区时的影响显著． 应力扰动主要对扰动加入的这个地震周期和地震大小产生显著影响， 对之后的地震序列影响则很小． 当应力扰动发生在地震滑移区时， 若应力扰动足够大， 压应力增大会造成地震发生时部分断层被锁住， 从而使得地震释放的能量变小. 但对这种情况， 后续地震会释放较大的能量， 即产生较大的地震． 这种效应在应力扰动越大时越明显． 应力扰动发生的时间对上述规律影响很小．

2） 断层面上压应力减小导致地震规律产生更加复杂的变化． 如果应力扰动足够大， 压应力减小会即时触发地震． 如果应力扰动发生在一个地震周期的早期， 则触发的地震会较小， 且导致随后的地震提前发生， 地震释放的能量也略微增大； 如果应力扰动发生在一个地震周期的后期， 则会触发大地震． 如果应力扰动足够小， 这种影响会减小， 即可能不会触发地震的发生． 但当应力扰动位于震前滑移区或破裂临界区时， 则小的扰动也可能产生类似的效果． 应力扰动加入越晚， 这种影响也越明显． 应力扰动发生在破裂临界区的影响最明显．

3） 值得注意的是， 小震的发生可减小地震发生区域的库仑应力， 但会增加未滑移断层面区域的库仑应力值． 由于增加的库仑应力值不足以导致整个断层发生破裂， 因而一般将导致后续大地震提前发生． 另外， 当在震前滑移区或在破裂临界区压应力减小时， 由于促使地震提前发生， 应变能积累减少， 一般后续地震矩相对较小． 而当应力扰动发生在地震滑移区时， 压应力减小会使断层更容易滑动， 从而产生更大的同震位移， 使得触发的大地震或触发的小地震后的大地震震级都明显增大．

4） 应力扰动的影响一般主要集中在应力发生变化的地震周期内． 后续地震基本恢复无应力扰动时的特征地震规律， 但后续特征地震规律也会受到一定影响， 使得地震复发周期和大小都会产生一定程度的变化．

应力扰动对断层滑动规律的影响非常复杂， 以上表现仅针对本文采用的简单模型． 本文虽然进行了大量计算， 但仍有许多后续工作需要进行， 例如不同摩擦准则的影响， 以及同一摩擦准则下不同参数变化的影响等． 此外， 实际断层的几何形态也比本文模型复杂很多； 断层几何特征， 如非平面断层等的影响也是后续研究需要进一步探讨的问题． 本文从物理模型出发， 利用数值方法结合断层滑移弱化摩擦准则研究了断层的活动规律， 这为后续复杂模型的计算奠定了基础．

本文的有限元模型解算采用PyLith软件， 感谢Aagaard等在软件方面提供的支持； 研究过程中与杨宏峰博士进行过多次有益的讨论． 在此一并表示感谢．

蔡永恩, 何涛, 王仁. 1999. 1976 年唐山地震震源动力过程的数值模拟[J]. 地震学报, 21（5）: 469--477.

Cai Y E, He T, Wang R. 1999. Modelling the source dynamic process of the 1976 Tangshan earthquake[J].ActaSeismologicaSinica, 21（5）: 469--477 （in Chinese）.

武艳强, 江在森, 王敏, 车时, 廖华, 李强, 李鹏, 杨永林, 向和平, 邵志刚, 王武星, 魏文薪, 刘晓霞. 2013. GPS 监测的芦山7.0级地震前应变积累及同震位移场初步结果[J]. 科学通报, 58（20）: 1910--1916.

Wu Y Q, Jiang Z S, Wang M, Che S, Liao H, Li Q, Li P, Yang Y L, Xiang H P, Shao Z G, Wang W X, Wei W X, Liu X X. 2013. Preliminary pertaining to the coseismic displacement and preseismic strain accumulation of the LushanMS7.0 earthquake, as reflected by the GPS surveying[J].ChineseScienceBulletin, 58（28/29）: 3460--3466.

朱守彪, 邢会林, 谢富仁, 石耀霖. 2008. 地震发生过程的有限单元法模拟： 以苏门答腊俯冲带上的大地震为例[J]. 地球物理学报, 51（2）: 460--468.

Zhu S B, Xing H L, Xie F R, Shi Y L. 2008. Simulation of earthquake processes by finite element method: The case of megathrust earthquakes on the Sumatra subduction zone[J].ChineseJournalofGeophysics, 51（2）: 460--468 （in Chinese）.

朱守彪, 张培震. 2009. 2008 年汶川MS8.0地震发生过程的动力学机制研究[J]. 地球物理学报, 52（2）: 418--427.

Zhu S B, Zhang P Z. 2009. A study on the dynamical mechanisms of the WenchuanMS8.0 earthquake, 2008[J].ChineseJournalofGeophysics, 52（2）: 418--427 （in Chinese）.

Aagaard B T, Knepley M G, Williams C A. 2013. A domain decomposition approach to implementing fault slip in finite-element models of quasi-static and dynamic crustal deformation[J].JGeophysRes, 118（6）: 3059--3079.

Bakun W H, McEvilly T V. 1984. Recurrence models and Parkfield, California, earthquakes[J].JGeophysRes, 89（B5）: 3051--3058.

Bakun W H, Lindh A G. 1985.TheParkfield,California,EarthquakePredictionExperiment[M]. Emmitsburg, MD: National Emergency Training Center: 619--624.

Bakun W H, Aagaard B, Dost B, Ellsworth W L, Hardebeck J L, Harris R A, Ji C, Johnston M J S, Langbein J, Lienkaemper J J, Michael A J, Murray J R, Nadeau R M, Reasenberg P A, Reichle M S, Roeloffs E A, Shakal A, Simpson R W, Waldhauser F. 2005. Implications for prediction and hazard assessment from the 2004 Parkfield earthquake[J].Nature, 437（7061）: 969--974.

Ben-Zion Y, Rice J R, Dmowska R. 1993. Interaction of the San Andreas fault creeping segment with adjacent great rupture zones and earthquake recurrence at Parkfield[J].JGeophysRes, 98（B2）: 2135--2144.

Brace W F, Byerlee J D. 1966. Stick-slip as a mechanism for earthquakes[J].Science, 153（3739）: 990--992.

Byerlee J. 1978. Friction of rocks[J].PureApplGeophys, 116（4/5）: 615--626.

Cai Y E, He T, Wang R. 2000. Numerical simulation of dynamic process of the Tangshan earthquake by a new method: LDDA[J].PureApplGeophys, 157（11/12）: 2083--2104.

Diao F Q, Xiong X, Wang R J, Zheng Y, Walter T R, Weng H H, Li J. 2013. Overlapping post-seismic deformation processes: Afterslip and viscoelastic relaxation following the 2011MW9.0 Tohoku （Japan） earthquake[J].GeophysJInt, 196（1）: 218--229

Duan B C. 2012. Dynamic rupture of the 2011MW9.0 Tohoku-Oki earthquake: Roles of a possible subducting seamount[J].JGeophysRes, 117: B05311. doi:10.1029/2011JB009124.

Elliott A J, Dolan J F, Oglesby D D. 2009. Evidence from coseismic slip gradients for dynamic control on rupture propagation and arrest through stepovers[J].JGeophysRes, 114: B02312. doi:10.1029/2008JB005969.

Fedotov S A. 1965. Regularities of the distribution of strong earthquakes in Kamchatka, the Kurile Islands and northeastern Japan[J].TrInstFizZemliAkadNaukSSSR, 36（203）: 66--93.

Fialko Y. 2006. Interseismic strain accumulation and the earthquake potential on the southern San Andreas fault system[J].Nature, 441（7096）: 968--971.

Igarashi T, Matsuzawa T, Hasegawa A. 2003. Repeating earthquakes and interplate aseismic slip in the northeastern Japan subduction zone[J].JGeophysRes, 108（B5）: 2249. doi:10.1029/2002JB001920.

Jackson D D, Kagan Y Y. 2006. The 2004 Parkfield earthquake, the 1985 prediction, and characteristic earthquakes: Lessons for the future[J].BullSeismolSocAm, 96（4B）: S397--S409.

Kato N, Hirasawa T. 1999. A model for possible crustal deformation prior to a coming large interplate earthquake in the Tokai district, central Japan[J].BullSeismolSocAm, 89（6）: 1401--1417.

Kato N, Tullis T E. 2001. A composite rate- and state-dependent law for rock friction[J].GeophysResLett, 28（6）: 1103--1106.

Kato N. 2003. A possible model for large preseismic slip on a deeper extension of a seismic rupture plane[J].EarthPlanetSciLett, 216（1/2）: 17--25.

Nadeau R M, McEvilly T V. 1999. Fault slip rates at depth from recurrence intervals of repeating microearthquakes[J].Science, 285（5428）: 718--721.

Reid H F. 1910. The California earthquake of April 18, 1906: Report of the State Investigation Commission[G]∥TheMechanicsoftheEarthquake. Washington: Carnegie Institution of Washington: 2--192.

Robinson D P, Das S, Searle M P. 2010. Earthquake fault superhighways[J].Tectonophysics, 493（3/4）: 236--243.

Ruegg J C, Rudloff A, Vigny C, Madariaga R, de Chabalier J B, Campos J, Kausel E, Barrientos S, Dimitrov D. 2009. Interseismic strain accumulation measured by GPS in the seismic gap between Constitución and Concepción in Chile[J].PhysEarthPlanetInter, 175（1/2）: 78--85.

Scholz C H. 1998. Earthquakes and friction laws[J].Nature, 391（6662）: 37--42.

Schwartz D P, Coppersmith K J. 1984. Fault behavior and characteristic earthquakes: Examples from the Wasatch and San Andreas fault zones[J].JGeophysRes, 89（B7）: 5681--5698.

Shearer P M. 2009.IntroductiontoSeismology[M]. Cambridge: Cambridge University Press: 2--15.

Sieh K E. 1978. Prehistoric large earthquakes produced by slip on the San Andreas fault at Pallett Creek, California[J].JGeophysRes, 83（B8）: 3907--3939.

Simpson R W, Schulz S S, Dietz L D, Burford R O. 1988. The response of creeping parts of the San Andreas fault to earthquakes on nearby faults: Two examples[J].PureApplGeophys, 126（2/3/4）: 665--685.

Stuart W D. 1988. Forecast model for great earthquakes at the Nankai trough subduction zone[J].PureApplGeophys, 126（2/3/4）: 619--641.

Swan III F H, Schwartz D P, Cluff L S. 1980. Recurrence of moderate to large magnitude earthquakes produced by surface faulting on the Wasatch fault zone, Utah[J].BullSeismolSocAm, 70（5）: 1431--1462.

Townend J, Zoback M D. 2004. Regional tectonic stress near the San Andreas fault in central and southern California[J].GeophysResLett, 31（15）: L15S11. doi:10.1029/2003GL018918.

Tsutsumi A, Fabbri O, Karpoff A M, Ujiie K, Tsujimoto A. 2011. Friction velocity dependence of clay-rich fault material along a megasplay fault in the Nankai subduction zone at intermediate to high velocities[J].GeophysResLett, 38（19）: L19301. doi:10.1029/2011GL049314.

Uenishi K, Rice J R. 2003. Universal nucleation length for slip-weakening rupture instability under nonuniform fault loading[J].JGeophysRes, 108（B1）: 2042. doi:10.1029/2001JB001681.

Wesnousky S G. 1994. The Gutenberg-Richter or characteristic earthquake distribution, which is it?[J].BullSeismolSocAm, 84（6）: 1940--1959.

Numerical simulations about the influence of stress disturbance on earthquake cycle and seismic moment

1）LaboratoryforEarthquakeandEarth’sInterior,SchoolofEarthandSpaceSciences,UniversityofScienceandTechnologyofChina,Hefei230026,China2）MengchengNationalGeophysicalObservatory,Hefei230026,China

The influences of stress disturbance on earthquake cycle were studied based on a 2D finite element model by employing a dynamic fault with slip-weakening friction law. Numerical results show that the stick-slip process of the dynamic fault in a model with uniform background stress behaves like typical characteristic earthquakes, which could be influenced by stress disturbance on the fault. Increasing pressure or decreasing normal stress on the fault delays the occurrence of the following earthquake and enlarges its size, which is more prominent if the stress disturbance locates on the critical rupture zone than on pre-seismic slip zone. If the increased pressure locates on the earthquake slip zone and is large enough, part of the dynamic fault could be locked temporally, thus decreasing the following earthquake size, but enlarging the next earthquake. The influence of decreasing pressure on the fault is more complicate than increasing pressure. If the decreased pressure is large enough, an earthquake could be triggered immediately. If the pressure is decreased at earlier stage of an earthquake cycle, the triggered earthquake usually is a small one, and the next earthquake happens at a shorter time than the time interval of the characteristic earthquakes; on contrary, if the pressure is decreased at later stage of an earthquake cycle, a large earthquake will be triggered immediately. If the stress disturbance locates on pre-seismic slip zone or critical rupture zone, a smaller stress disturbance could produce a similar result; and the later disturbance happens, the more prominent the influence is. The influences are the most prominent when disturbance locates on critical rupture zone. It should be pointed out that the influences of stress disturbance are usually confined within one or two earthquake cycles, and the following earthquake cycles are nearly identical with those without stress disturbance.

characteristic earthquake; finite element numerical simulation; slip-weakening friction law; stress disturbance

10.11939/jass.2015.01.006.

国家自然科学基金项目（41474082, 91014005）资助.

2014-05-05收到初稿， 2014-08-25决定采用修改稿.

e-mail: qfkq7850@mail.ustc.edu.cn

10.11939/jass.2015.01.006

P315.72+7

A

翁辉辉， 黄金水. 2015. 应力扰动对地震周期和地震矩影响的数值模拟. 地震学报, 37（1）: 65--79.

Weng H H, Huang J S. 2015. Numerical simulations about the influence of stress disturbance on earthquake cycle and seismic moment.ActaSeismologicaSinica, 37（1）: 65--79. doi:10.11939/jass.2015.01.006.