2007年5月—2013年12月成都、 西昌和重庆台地磁转换函数的时间变化

龚绍京 刘双庆 张明东

（中国天津300201天津市地震局）



2007年5月—2013年12月成都、 西昌和重庆台地磁转换函数的时间变化

（中国天津300201天津市地震局）

本文较详细地讨论了地磁转换函数的计算方法， 介绍了复转换函数实部和虚部的误差公式．利用成都、 西昌和重庆3个地磁台2007年5月—2013年12月的地磁数字化资料， 计算出转换函数A，B及帕金森矢量．结果表明， 在2008年汶川MS8.0地震前后成都台存在可察觉的小鼓包， 而西昌、 重庆两台则没有可察觉的异常．另外与20世纪80年代的结果比较， 汶川地震前后成都台的b值和帕金森矢量的长度及方向都有明显的长期变化.

地磁转换函数 复数最小二乘法 多元回归分析 稳健估计 帕金森矢量 地震异常

引言

1940年贾普曼最早提出地壳的不规则性可能会影响地磁场尤其是较短周期的瞬变场（Chapman, Bartels, 1940）, 这一论点已被20世纪50—60年代发现的大量事实所证实． Parkinson （1959）通过研究快速地磁变化矢量的方向， 发现地磁变化矢量有限定在一个平面上的趋势, 此平面被称为“地磁变化矢量优势面”. 在此基础上提出了帕金森矢量的概念， 推导出著名的帕金森矢量系数经验公式． 大量研究表明， 帕金森矢量有3种反映地下电性结构的效应： 内陆异常、 海岸效应和电流通道（Parkinson, 1959, 1962； Untiedt, 1970； 龚绍京, 1987）．

此后引入具有严格周期概念的转换函数， 它表达输出与输入之间的函数关系， 用以描述复频率域内线性系统的动态特性． 在地磁领域， 输入是外源施感场， 输出是内源感应场． 由于分解地磁内外源场很困难且需较多台站资料， Schmucker（1970）引入正常场和异常场的概念， 假设外源场准均匀， 经近似简化处理推导出较简便且实用的表达形式， 使单台和双台地磁复转换函数的实际应用成为可能并取得许多成果． 按Schmucker的概念， 当地下电性结构为水平分层且横向比较均匀时， 其转换函数值很小； 垂直场转换函数及由它们组成的帕金森矢量的长度反映地下电性的横向不均匀程度， 矢量指向导电率高的一方．

20世纪70年代以来， 国外许多研究人员利用研究地下电性结构的参数来探寻地震引起的地下电性变化， 出现明显异常的有关东地震（Yanagihara， 1972）、 塔什干地震（Miyakoshi， 1975）、 锡特卡地震（Rikitake， 1979）和卡莱尔地震（Beamish， 1982）． 从20世纪80年代起， 作者利用磁变仪资料， 采用量图和磁照图数字化方法， 计算帕金森矢量系数a和b（Gong， 1985； 龚绍京等， 1989； 林美， 龚绍京， 1991）、 单台垂直场转换函数A和B（龚绍京等， 1991）以及水平场台际转换函数C、G、E、F（龚绍京等， 1997， 2001）， 发现在唐山、 松潘、 菏泽、 花莲地震前后均存在或大或小、 或长或短的异常． 特别对唐山地震， 作者研究了上述所有参量， 发现a（Gong， 1985）和Au、Cu、Cv、Fv在唐山地震前后有持续约5—7年的异常， 震后一段时间才恢复（龚绍京等， 1997）； 同时水平场转换函数C和F在震前的1976年2—4月出现十分明显的短期前兆， 这是1972—1997年26年间出现的唯一一次短期前兆（龚绍京等， 2001）． 陈伯舫（1998）也研究了关岛等地震， 同样发现了这些参数的异常．

对复转换函数的计算， Beamish （1982）采用功率谱互谱方法， Everett和Hyndman （1967）以及作者采用复数最小二乘法（龚绍京等， 1991， 1997， 2001）． 国内一些研究人员对转换函数也提出了各自的计算方法和公式， 对其中某些问题龚绍京等（2012）已经作过分析. 本文拟对新发现的问题进行分析探讨．

2007—2008年间， 我国的大部分地磁相对观测已改用磁通门磁力仪， 实现了数字化记录． 随着计算科学的发展出现了许多新的计算语言， 为适应这些新的变化， 作者将过去龚绍京编的Fortran语言程序改编成Matlab语言程序*在改编程序的课题中， Matlab程序的大部分内容如提取数据、 显示图形、 消除干扰、 显示菱形截取数据等由刘双庆编写. 复数最小二乘法求转换函数及实、 虚部误差的计算， 稳健估计的应用以及求帕金森矢量部分由龚绍京编写.， 并用新程序计算了成都、 西昌、 重庆3个地磁台的转换函数A，B和帕金森矢量， 拟探讨汶川MS8.0地震前后是否存在异常现象．

1 转换函数计算方法， 公式及讨论

1.1 帕金森矢量系数

帕金森矢量系数经验公式为

ΔZ=a·ΔH+b·ΔD，

（1）

1.2 复转换函数计算方法及实部和虚部的误差公式

经简化处理后的地磁复转换函数表达式为

Z=A·H+B·D+εz，

（2）

（3）

式中：A，B为单台垂直场转换函数；C，G，E，F为水平场台际转换函数；ε为残差. 这些参数皆为复数且是频率的函数． 下标“a”代表异常场， “n”代表正常场， “k”代表异常区台站的磁场． 对于式（2）、 （3）的常规计算方法请参阅相关文献（Everett, Hyndman, 1967; 龚绍京等, 1991, 1997, 2001）， 但其中未给出A，B实部和虚部的误差公式.

用复数最小二乘法推导的计算复转换函数的公式为

（4）

其中

（5）

A、B实部和虚部的误差公式由本文第一作者采用单位矢量法和拉格朗日乘数法则推导， 并曾寄给陈伯舫博士验证．A实部与虚部的误差公式为

（6）

同理也可推导出B实部与虚部误差公式为

（7）

1.3 转换函数计算方法讨论

由于Matlab语言为诸多数学问题提供了成熟的子函数程序， 有人提出了与复数最小二乘不同的算法， 即将等式两边除同一变量， 将联立方程组中的复系数和复变量分解成实部和虚部， 再采用多元回归分析处理方程数倍增的联立方程组． 例如对式（2）进行如下变换得到式（8）.

令Z/D=Tr+iTi，S=H/D=Sr+iSi， 则T=A·S+B+ε. 由此可以得到

（8）

式中所有元素都为实数， 有4个待定参数， 变成2m个方程． 调用Matlab中的多元回归（regress）子函数可求出4个系数值．

然而， 依据式（8）调用regress子函数得到的结果与依据复数最小二乘法（式（4））得到的结果有一定差别， 有时差别还相当大， 如图1所示． 显然图中“方法1”（姑且称之为‘多元回归分析法’）的离散度较采用复数最小二乘的“龚算法1”大， 效果差一些． 起初找不到导致这种差别的原因， 尝试了多方面的分析对比研究． 当确认式（4）推导无误后， 曾怀疑是否多元回归子函数计算的结果与复数最小二乘的结果不同， 但最终找出了出现差别的原因： 变换使式（8）与式（2）的残差表达式不同， 因而对残差平方和偏微商的结果也不相同． 为此用数字试验的办法进行了验证， 即用复数最小二乘法的式（4）去计算经变换（除D）后的数据， 用T代替式（5）中的Z， 用S代替H，D则为1． 所得到的结果与调用多元回归子函数的结果完全一样．

图1 成都台2007年9月22—28日（a）与2009年7月11—21日（b）的周期响应曲线

同时对最简单的情形进行了研究. 设z=a·x+b·y， 式中的元素均为实数． 用y（或x）去除等式的两边． 如果是确定性问题， 即如果是解方程， 那么， 未进行变换得到的a、b值与进行变换后得到的a、b值相同． 但如果用最小二乘法进行“估算”， 由于存在残差， 数字试验表明， 进行变换与未变换的两种估计值是有差别的． 估计值的残差越小， 越接近确定性问题的解， 两种算法的差别也越小； 残差越大， 两种方法的差别也越大． 这从图1中也可得到证实． 图1中的周期响应曲线仅用了式（4）和（8）的计算结果， 未引入稳健估计．

1.4 稳健估计方法效果评价

稳健统计方法是在加权统计方法基础上发展起来的， 其中心思想是选择某种统计量， 使理想假设不受某些偏离数据的影响， 并引入“极端点”（outlier points）的概念， 以便自动识别偏离的数据和自动修正所加之权重， 通过反复迭代使估计值趋于稳定． 关于稳健（Robust）估计的原理和做法详见Egbert和Booker（1986）以及龚绍京等（1997， 2001）文章．

具体进行稳健估算时， 需设定两个控制参量， 即加权时用到的损失函数以及迭代终止的判据． 作者共设计了3种稳健估计， 其中一种调用了Matlab中的子函数. 图2给出了3种稳健估计的周期响应曲线. 可以看出， 用方法1（式（8））得到的实线与本文用虚线表示的3种稳健估计曲线存在差异， 而3种虚线的差别在图中几乎看不出来， 仅数值有小的差别． 这也进一步验证了作者过去和现在所采用方法的可靠性．

图2 3种稳健估计方法的周期响应曲线

Fig.2 Period respond curves of three robust estimations. The solid line denotes the result by method 1, and the dotted line denote three kinds of robust estimate methods

2 资料处理

2.1 资料来源及可靠性分析

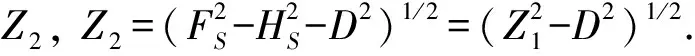
表1 用Z2与实测Z得到的转换函数之比较Table 1 Comparison between transfer functions calculated by using Z2 and measured Z value

注： 表中某些周期值实际代表一定的周期范围, 即34.4（32.0—36.57）， 25.9（23.27—28.44）， 19.2（17.07—21.33）， 14.1（12.19—16.0）， 10.1（8.53—11.64）， 括号内为其范围.

本文使用经高斯滤波预处理的分钟值， 计算转换函数时没有进行高通滤波． 由于一些小的干扰可能没有被发觉， 或没有办法识别、 消除， 因此短周期的结果并不稳定． 同时由于采取端点去倾， 数据没有零均值化， 使得存在快速傅里叶变换的非零直流项（第一项）． 由于本文快速傅里叶变换的样本长度不算很长， 所以还会有谱线扩散问题． 当3个分量的时间曲线大多集中在起、 终点连线一侧时， 非零直流项有时可能会较大， 以致于影响长周期的结果． 因此本文在研究转换函数的时间变化时， 只取周期为10—64min的值.

2.2 事件选取

用数字化资料计算复转换函数， 需利用地球变化磁场的短周期成分． 鉴于要进行谱分析， 因此需选用有连续扰动的时段， 也可以包含急始、 湾扰和脉动等． 而量图求a, b的方法仅选典型的地磁短周期变化如急始、 类急始、 湾扰和孤立的扰动． 根据作者的经验和数据的预处理方法以及当前仪器的状态， 本文提出如下事件选取原则： ① 选取目标周期成分， 根据过去的工作总结出一些地震出现异常的周期（表2）， 可供参考． ② 避开3个分量的日变化， 尽量在夜间的时段选取． ③ 避开和识别包括仪器、 环境在内的各种干扰, 有些干扰持续时间较短， 可以用线性内插的办法改正． ④ 一般不选特别激烈扰动， 因激烈的扰动可能不能满足源场准均匀的假设． 由于源场不均匀产生的源场效应会造成估计值的涨落, 为此尽量选全球同时发生的事件， 不选地方性扰动如钩扰． ⑤ 遇到缺数出现99999时， 如时间不长可以用线性内插的办法补数． ⑥ 起止点要选在比较平坦的位置而不是快速变化的途中， 要兼顾H和D的变化， 还要两头兼顾． 由于是端点线性去倾， 如果起止位置处在一个相近水平则最好, 如不能满足上述条件， 则起止点也要选在拐点（停顿）或极值点的位置（图3）． ⑦ 需要注意识别Z的较长周期成分是否由于H和D的变化所引起， 如果不是， 则会影响长周期的转换函数结果， 这种情况我们曾遇到过.

表2 几个震例中异常的最大周期Table 2 The maximum periods of anomalies for several examples of earthquakes

注：ΔZ/ΔH用的是前沿时间， 大体相当于半周期．

本文采取3个台同时挑选事件的办法． 为便于识别Z的变化， 作图3时3个台的Z都放大了1倍. 可以看出, 3个台的H和D变化大体相同， 但Z变化不同； 还可看出重庆台的Z受H的影响较明显， 成都台的Z受D的影响较明显， 而西昌台受H和D的共同影响较明显． 这反映了地下电性结构的差异． 根据龚绍京（1983）对地磁短周期事件时间序列的分析， 选m=12—16计算一组转换函数， 多数都是13—15个事件． 由于是分钟值， 所能挑选的事件数和所能求出的周期都会受到限制， 无法求出更短周期的转换函数， 好在以往震例显示10—48min周期的转换函数也能很好地检测到异常（表2）． 每组转换函数所占的时间跨度视事件多少而变， 一般7—10天求一组， 也有5天可求一组的； 数据不好时半个月或更长时间才能求出一组． 以每个时间跨度的中点日期代表该组转换函数的时间点， 误差仅有半天.

图3 事件选取示例（事件起止时间： 2009年7月20日14:12—18:28．

3 结果分析

3.1 成都台两种时间变化曲线的比较

本文首先研究了最初得到的数据， 绘制出Au， Av， Bu和Bv的时间变化曲线． 10—64min的周期范围可以画出8条时间变化曲线， 但图形显得“很挤”. 为此选择了6条曲线， 其对应的周期从下至上分别是： 51.2， 42.7， 34.4， 29.5， 19.2和10.1min（图4）． 除Au在地震前后有所变化外（图4a）， 其它几条曲线都未显示出明显变化， 且Bu和Bv的涨落较大， 限于篇幅仅列出Au图． 图4a中， 2007—2008年用M15预处理分钟值， 2009年开始用GM4预处理分钟值， 其中2008年1月26日至年底的Z数据因受潮不可靠． 由图4a可看出， 42.7， 34.4和29.5min这3个周期成分在地震发生前后有明显的“鼓包”. 只是由于仪器受潮， 不能确信上述“鼓包”就是异常， 需用Z2数据绘出图4b以相互佐证.

图4b中， 2007年用M15预处理数据， 2008年1月—5月19日用计算的Z2值， 5月20日09时07分开始用GM4预处理数据． 可以看出, 图4a与图4b在2008年的形态是不同的． 但仔细查看， 会发现在地震发生和紧随其后不长的时间内（即图4a出现“鼓包”的时段内）， Au曲线有可察觉的上升， 即Au绝对值减小． 而从图4b还可看到震前有一不太深的“凹陷”（42.7， 34.4， 29.5和10.1min）， 即Au的绝对值变大． 有意思的是， 芦山地震前似乎也有一点“凹陷”．

3.2 3个地磁台时间变化曲线的比较与分析

图5给出了西昌台和重庆台的Au时间曲线， 图中数据均来自GM4． 可以看出， 2007—2009年上半年两个台站的Au值都很平稳， 没有异常． 西昌台自2009年下半年以后Au值涨落较大， 说明有来自仪器和环境的干扰． 对于成都台的结果, 作者认为异常应遵从成片原则： ① 要有多个周期同时出现异常； ② 要有连续多个点同时出现异常． 图4a的异常是明显的， 但地磁台网中心认为那段资料不可靠， 尽管本文在选择事件时已排除了可以察觉到的不正常情况， 但仍可能有人眼不能察觉的因素影响了数据． 图4b的结果是对图4a的佐证， 尽管图形不太一样， 但大部分周期的时间曲线均在汶川地震前有一个下降的趋势， 并在地震时回升， 以10.1， 34.3和42.7min3个周期较明显． 图4中的曲线下降表明Au的绝对值增大， 说明地下电性的横向不均匀性增加． 地震时Au绝对值变小， 曲线回升．

图5 （a） 西昌台Au时间曲线（Au为正值）; （b） 重庆台Au时间曲线（Au为正值， 2011年11月以后为重庆附近的仙女山台资料）

为了更好地考察成都台转换函数的变化， 本文用成都台GM4资料的Au和Bu求出实帕金森矢量的长度Lr和方位角Fr， 并求出Au， Bu， Lr及Fr的均值（图6）， 求均值所取的时间跨度参考图4b． 图6中， 在汶川和芦山地震前成都台均表现为Au下降（绝对值增大）， 地震时及震后（2008年5—6月和2013年4—7月）Au上升． 对于汶川地震， 25.9—64.0min周期的Au是在地震发生时上升至最大， 而10.1—19.2min周期的Au是在震后达到最大; Bu的大多数周期在地震时有所增大， 而震前相对较低; Fr表现为在两个地震时或震后减小， 对汶川地震， 短周期成分的减小要滞后一点， 表明深层Fr的变小先于浅层． 帕金森矢量长度Lr规律性较差， 这与D的记录值为“分”， 由“分”换算成“nT”的换算系数接近“10”， 因而Bu值误差较大有关． 但还是能找到一些规律， 如Lr较大的周期是25.9， 34.4和42.7min， 以34.4min最大， 说明这些周期对应的深度电性结构横向不均匀性较大． 又如10.1， 14.1， 34.4和42.7min周期的Lr在汶川地震前已变大， 19.2， 25.9， 51.2和64.0min则在震时变大， 说明在地震前或地震时电性的横向不均匀性有所增加． 帕金森矢量的方位角Fr变小， 表明帕金森矢量的指向往地震发生的方向移动． 也说明上述括号中两个时段的Au绝对值变小是由于帕金森矢量的方向变化所致． 成都台的Lr值变大和Fr变小是重要的异常标志． 然而， 这只是一种短期的前兆， 是否有更长期的异常变化还有待研究．

图6 成都台转换函数A的实部Au, B的实部Bu以及实帕金森矢量的长度Lr和方位角Fr的均值变化

3.3 成都台转换函数和帕金森矢量的长期变化

成都、 西昌、 重庆台2007年5月以前无磁通门磁力仪资料． 由于客观条件的限制， 本文作者目前未能收集磁变仪资料并将其数字化， 以求出复转换函数， 只好与以前在成都台用量图方法做的a， b对比（龚绍京等， 1989）． 该文量取地磁短周期变化事件（如急始、 类急始、 各类孤立的扰动等）的前沿时间Δt及相应的ΔZ，ΔH，ΔD， 其持续时间Δt只能与本文14.1和10.1min周期的结果（对应的周期范围是8.5—16.0min）对比． 为考察是否存在长期变化， 表3列出了成都台2009—2011年的均值.

表3 成都台2009—2011年Au, Bu, Lr和Fr的均值及其误差Table 3 The average values and corresponing errors of Au, Bu, Lr， Frat the Chengdu station in 2009—2011

注: 误差dAu,dLr,dFr和dBu是2009—2011年3年的平均误差， 而不是平均值的标准差．

图7 成都、 西昌和重庆台的帕金森矢量（Δt=3—10 min）

成都、 西昌、 重庆3个台不同周期范围的帕金森矢量示于图7． 可以看出， 成都台的帕金森矢量指向龙门山断裂带并有较长期的变化， 黑色箭头是20世纪80年代的结果， 黄色箭头为表3的结果， 两箭头相差约27°． 重庆台的帕金森矢量比另两个台都长， 其指向背离四川盆地． 西昌台的帕金森矢量指向西南， 不同周期帕金森矢量的指向有差别．

帕金森矢量是一个用地磁方法反映地下电性结构的参量， 它的长度越大， 表示地下电性横向不均匀的程度越高． 其方向指向导电率高的一方， 例如它会垂直于海岸线总的走向或指向附近的深海． 在北半球， 它的画法是由磁南右旋Fr角． 在地理坐标中需考虑偏角的年均绝对值Ds， 例如Ds为-1.7°、 Fr=108.3°表示与磁北的夹角是-71.7°， 则帕金森矢量与地理北的夹角是-1.7°-71.7°=-73.4°． 帕金森矢量的物理意义和求法见Parkinson（1959， 1962）与龚绍京（1987）等文章． 用1979—1987年成都台的a与b均值求出帕金森矢量， 其长度L=0.13， 方位角F=171.5°， 与地理北的夹角为-10.1°． 而2009—2011年成都台周期为8.5—16.0min的实帕金森矢量长度Lr=0.182±0.021， 方位角Fr=144.8°±8.3°， 与地理北的夹角为-36.9°， 变化超出了2倍误差． 该结果与龚绍京和刘双庆（2012）的初步结果吻合， 只是该文用的是未经预处理的分钟值， 本文用的是经过预处理的分钟值资料．

量图方法得出的a与b没有严格的周期概念， 因此这种对比是很粗糙的． 为了进一步验证转换函数和帕金森矢量的长期变化， 作者在计算机上处理了2011年4—6月的资料， 量取了Δt，ΔD，ΔH，ΔZ值， 67组数求出的结果为 a=-0.1123， b=0.1412， L=0.1776， F=128.5°． 由a和b求得的帕金森矢量与地理北的夹角为-53.2°， 与1979—1987年在磁照图上的量图结果相比， b， L和F都有很大变化， 甚至比Fr的变化还大（表4）．

表4 成都台地磁短周期变化参量的长期变化Table 4 The long-term changes in geomagnetic short-period variation parameters at the Chengdu station

4 讨论与结论

综合上述分析， 本文得出以下几点看法：

1） 无论是求a与b还是求A与B， 都不应该进行变换， 即不能在等式两边除同一变量然后作回归分析． 对求a和b要进行二元回归分析． 对复转换函数A和B， 最早和大量使用的都是式（4）． 如用多元回归分析， 所求系数和方程数都将增加一倍．

2） 无论是用量图方法得到的a， b， L， F， 还是用谱分析方法得到的Au， Bu， Lr， Fr， 与20世纪80年代成都台的结果相比较， 都显示转换函数和帕金森矢量有明显的长期变化． b， L和F的变化比较大， 而a的长期变化不大． L增大说明这些年该地区地下电性横向不均匀程度增加， F变小说明帕金森矢量的方向朝地震发生的区域移动．

转换函数的长期变化已有柿岗台（Yanagihara， 1972）和广州台的例子（林美， 龚绍京， 1991）． 前者与1923年关东大地震有关， 后者处理了1960—1987年共28年资料， 其长期变化也许与菲律宾板块和欧亚板块的相对运动或是大陆架隆起因而海水变浅有关.

为了准确而严格地考察成都台各种周期的长期变化及变化过程， 需将1975—2007年的磁变仪资料数字化， 计算复转换函数并求出实、 虚帕金森矢量．

3） 汶川和芦山地震前后Au有一点略可察觉的短期变化. 从图6可看出, Lr, Bu和Fr也在同期有所变化， 但这些变化都不显著． 作者过去的研究表明， 垂直场转换函数在唐山地震前后有5—7年的中长期变化（龚绍京等， 1985， 1997）， 但并未发现明显的短期前兆． 只是水平场转换函数有十分明显的短期异常（龚绍京等， 2001）． 因此汶川地震前后Au等的短期变化量不大是可以理解的．

4） 西昌和重庆台在这两次大地震前后没有可察觉的异常变化， 这从一个侧面说明成都台在地震前后的可察觉变化也许与地震有关．同时， 唐山地震和本文结果均说明地磁转换函数的异常范围是不大的． 其异常的范围还与构造带的产状或余震区的形状有关． 例如离唐山地震震中180km的白家疃台无异常， 但震中距110km的天津青光台却有异常． 这是因为唐山地震的断裂带和余震区呈北东—西南长条分布． 成都台对相距180km的松潘地震有反应， 也是因为该地震离龙门山断裂带较近． 但西昌和重庆台则离龙门山断裂带较远．

5） 本文成都、 西昌、 重庆3个地磁台的Au值及以前的一些研究结果均表明， 转换函数值在正常情况下都比较稳定， 即使出现‘突跳’等情况， 其变化幅度也不会超出一个量级． 这与袁宝珠等（2009）的结果形成鲜明对比． 对其所引用的方法和计算公式作者已经作过分析（龚绍京等， 2012）． 由于转换函数反映的是地下的电性结构， 在无异常、 无干扰、 无仪器故障的情况下给出的转换函数值表现出‘稳定’才是正常的．

感谢中国地震局地球物理研究所地磁台网中心主任杨冬梅研究员对我们工作的大力支持， 特别感谢地磁台网中心张素琴副研究员不厌其烦地多次为我们拷贝数据．

陈伯舫. 1998. 关岛8.1级大地震和地磁转换函数时间变化的关系[J]. 地震学报， 20（2）： 217--219.

ChenPF. 1998.TheGuangreatearthquake（Msz=8.1）andtimechangesingeomagnetictransferfunctions[J]. Acta Seismologica Sinica, 20（2）： 217--219 （inChinese）.

龚绍京. 1983. 青光台地磁短周期事件的时间序列分析[J]. 地震， （1）: 6--10.

GongSJ. 1983.TheanalysisonthetimeseriesofshortperiodgeomagneticeventatQingguangseismographicstation[J]. Earthquake, （1）: 6--10 （inChinese）.

龚绍京, 吴占峰, 蒋邦本. 1984. 地磁场瞬时扰动ΔZ/ΔH的异常变化[J]. 地震科学研究， （5）: 48--51.

GongSJ,WuZF,JiangBB. 1984.TheanomalouschangesofΔZ/ΔHoninstantaneousdisturbanceofgeomagneticfield[J]. Research of Seismological Science, （5）: 48--51 （inChinese）.

龚绍京. 1987. 广东省地磁台的帕金森矢量及广州台系数在河源地震前后的时间变化[J]. 地震研究， 10（5）: 575--582.

GongSJ． 1987.ParkinsonvectorsatthegeomagneticstationsinGuangdongProvinceandthetime-dependentchangesoftheirratioatGuangzhoustationbothbeforeandaftertheHeyuanearthquake[J]. Journal of Seismological Research, 10（5）: 575--582 （inChinese）.

龚绍京， 王伯维， 于彬. 1989. 松潘地震前后地磁转换函数的变化[C]∥松潘地震预报学术讨论会文集. 北京： 地震出版社: 95--98.

GongSJ，WangBW，YuB. 1989.ChangesofgeomagnetictransferfunctionsbeforeandafterSongpanearthquake[C]∥The Collected Works for Symposium About Forecasting Songpan Earthquake.Beijing:SeismologicalPress: 95--98 （inChinese）.

龚绍京， 杨桂君， 田山， 于彬. 1991. 菏泽5.9级地震前后菏泽台转换函数随时间变化的研究: 兼与王锜同志商榷[J]. 地震学报， 13（1）: 113--120.

GongSJ,YangGJ,TianS,YuB. 1992.ResearchonthetimechangesoftransferfunctionsatHezeobservatorybeforeandafterHezeearthquakeofmagnitude5.9:AdiscussionwithWangQi[J]. Acta Seismologica Sinica, 5（1）: 187--195.

龚绍京， 陈化然， 张翠芬， 马淑芹， 杨桂君. 1997. 地磁水平场转换函数在唐山地震前的异常反应[J]. 地震学报， 19（1）: 51--58.

GongSJ,ChenHR,ZhangCF，YangGJ，MaSQ. 1997.TheanomalousreactionsofthegeomagnetichorizontalfieldtransferfunctionsbeforeTangshanearthquake[J]. Acta Seismologica Sinica, 10（1）: 61--70.

龚绍京， 田真丽， 戚成柱， 何淑敏， 阎哓梅， 陈化然， 栗连弟. 2001. 地磁水平场转换函数的短期前兆[J]. 地震学报， 23（3）: 280--288.

GongSJ,TianZL,QiCZ,HeSM,YanXM,ChenHR,LiLD. 2001.Shorttermprecursorofthegeomagnetichorizontalfieldtransferfunctions[J]. Acta Seismologica Sinica, 14（3）： 293--302.

龚绍京， 刘双庆. 2012. 汶川M8.0地震前帕金森矢量的变化[G]∥王子昌先生诞辰百年纪念文集. 北京： 北京大学出版社： 45--51.

GongSJ,LiuSQ. 2012.ThechangeofParkinsonvectorbeforetheWenchuanM8.0earthquake[G]∥The Collected Works for Centennial of Wang Zichang Professor.Beijing：PekingUniversityPress： 45--51 （inChinese）.

龚绍京， 马骥， 刘双庆， 栗连弟. 2012. 对《转换函数与汶川大地震关系的初步研究》一文的分析[J]. 国际地震动态， （8）: 20--26.

GongSJ,MaJ,LiuSQ,LiLD. 2012.Commenton“StudyontherelationshipbetweentheWenchuanstrongearthquakeandthegeomagnetictransferfunction”byBaozhuYuanetal[J]. Recent Developments in World Seismology, （8）: 20--26 （inChinese）.

林美， 龚绍京. 1991. 广州台转换函数的长期变化和季节变化[J]. 地震学报， 13（4）: 480--488.

LinM,GongSJ. 1992.SecularandseasonalchangesintransferfunctionatGuangzhougeomagneticobservatory[J]. Acta Seismologica Sinica, 5（3）: 587--595.

袁宝珠， 陈化然， 张素琴， 李琪， 杨冬梅， 朱荣， 刘晓灿. 2009. 地磁转换函数与汶川大地震关系的初步研究[J]． 国际地震动态, （7）: 69--75.

YuanBZ,ChenHR，ZhangSQ，LiQ，YangDM,ZhuR,LiuXC. 2009.StudyontherelationshipbetweentheWenchuanstrongearthquakeandthegeomagnetictransferfunction[J]. Recent Developments in World Seismology, （7）: 69--75 （inChinese）.

BeamishD. 1982.Ageomagneticprecursortothe1979Carlisleearthquake[J]. Geophys J R astr Soc, 68（2）: 531--543.

ChapmanS，BartelsJ. 1940. Geomagnetism[M].Oxford:ClarendonPress: 1049.

EgbertGD,BookerJR． 1986．Robustestimationofgeomagnetictransferfunctions[J]. Geophys J R astr Soc, 87（1）: 173--194.

EverettJE,HyndmanRD. 1967．Geomagneticvariationsandelectricalconductivitystructureinsouth-westernAustralia[J]． Phys Earth Planet Inter, 1（1）: 24--34.

GongSJ． 1985．Anomalouschangesintransferfunctionsandthe1976Tangshanearthquake（MS=7.8）[J]. J Geomag Geoelectr, 37（4）： 503--508.

GongSJ,ChenPF,YangGJ. 1991.Researchonthetimechangesofinter-stationtransferfunctionsforthehorizontalgeomagneticfieldandtheirrelationshipwiththeHualian7.6earthquakeinTaiwanregion[C]∥International Conference of Seismicity in Eastern Asia.HongKong,October1991.

MiyakoshiJ. 1975.SecularvariationofParkinsonvectorsinaseismicallyactiveregionofMiddleAsia[J]. J Fac General Education, Tottori Univ, 8: 209--218.

ParkinsonWD． 1959．Directionsofrapidgeomagneticfluctuations[J]． Geophys J R astr Soc， 2（1）： 1--14.

ParkinsonWD． 1962．Theinfluenceofcontinentsandoceansongeomagneticvariations[J]. Geophys J R astr Soc, 6（4）: 441--449.

RikitakeT. 1979.Changesinthedirectionofmagneticvectorofshort-periodgeomagneticbeforethe1972Sitka,Alaska,earthquake[J]. J Geomg Geoelectr, 31（4）: 441--448.

SchmuckerU. 1970.AnomaliesofgeomagneticvariationsinthesouthwesternUnitedStates[J]． Bull Scripps Inst Oceanogr, 13： 1--165.

UntiedtJ. 1970.ConductivityanomaliesincentralandsouthernEurope（Appendix）[J]. J Geomag Geoelectr, 22（1/2）: 131--149.

YanagiharaK. 1972.SecularvariationoftheelectricalconductivityanomalyinthecentralpartofJapan[J]. Memo Kakioka Mag Obs, 15: 1--11.

Time changes in the geomagnetic transfer functions at Chengdu, Xichang and Chongqing stations from May 2007 to December 2013

（EarthquakeAdministrationofTianjinMunicipality,Tianjin300201,China）

This paper discusses the method for computing geomagnetic transfer functions in detail and introduces the error formulae of the real and imaginary parts of complex transfer functions. And then the transfer functionsAandBas well as Parkinson vectors are calculated by using the digital geomagnetic data recorded at the stations Chengdu, Xichang and Chongqing from May 2007 to December 2013. The results show that there are perceptible small bulges at Chengdu station before and after the 2008 WenchuanMS8.0 earthquake, but the other two stations do not exhibit perceptible anomalies. Comparison with the results in the 1980s indicates that obvious long-term variations of thebvalue as well as the length and direction of Parkinson vectors are observed at the station Chengdu.

geomagnetic transfer function; complex least squares method; multiple regression analysis; robust estimation; Parkinson vector; earthquake anomaly

10.11939/jass.2015.01.013.

天津市地震局局长科研基金资助.

2014-03-04收到初稿， 2014-06-03决定采用修改稿.

e-mail: caogong2003@hotmail.com

10.11939/jass.2015.01.013

P315.72+1

A

龚绍京, 刘双庆, 张明东. 2015. 2007年5月—2013年12月成都、 西昌和重庆台地磁转换函数的时间变化. 地震学报, 37（1）: 144--159.

Gong S J, Liu S Q, Zhang M D. 2015. Time changes in the geomagnetic transfer functions at Chengdu, Xichang and Chongqing stations from May 2007 to December 2013.ActaSeismologicaSinica, 37（1）: 144--159. doi:10.11939/jass.2015.01.013.