谱时程比方法及其在确定地铁沿线地层场地响应中的应用

王 博 雷 军

（中国北京100871北京大学地球与空间科学学院）



谱时程比方法及其在确定地铁沿线地层场地响应中的应用

（中国北京100871北京大学地球与空间科学学院）

利用在北京地铁4号线北京大学东门站附近地铁隧道内和地面场地观测得到的振动数据， 提出一种基于独立信号的谱时程比方法， 实现了从地铁振动和地面振动数据中提取地层场地响应信息以及土层中的振动衰减信息． 该方法对同一观测点不同时间段观测数据的分析结果具有高度的稳定性， 经验证与基于钻孔资料地层模型的半无限空间层状介质的理论传递函数的频率响应特征具有良好一致性． 同时， 基于该方法还对隧道壁与土层振动耦合以及观测点附近浅表土层非弹性吸收带来的综合等效衰减特征进行了评估． 研究结果显示， 北京大学东门站附近振动场地放大效应的峰值频率主要在3—10 Hz之间， 受地铁振动的影响， 场地效应在不同测点以及地铁沿线、 切线和铅垂线等3个不同方向显示出一定的差异．

地铁振动 场地响应 峰值频率 衰减

引言

随着城市现代化建设的发展， 城市轨道交通已成为人们生活中不可缺少的一部分． 由于地铁穿过城市的中心区， 在给人们生活提供方便的同时不可避免地对不同场地条件下的居民区、 科研院所、 医院、 古建筑等带来不同程度的振动干扰或不利影响． 了解和研究地铁沿线和附近场地的振动特征及地表土层对振动的衰减作用已经成为防治城市地球物理环境灾害问题中亟待解决的科学问题（雷军等， 2010， 2013）．

关于场地振动响应的问题在地震工程、 环境振动工程等不同学科中都被广泛地关注． 尽管各领域研究的侧重点有所不同， 但其面临的科学问题和解决问题的方法都是相近和互通的． 首先被人们注意到的是地震发生时不同场地条件下宏观震害存在显著的差异． 1906年美国旧金山大地震后Wood（1908）即对旧金山地区内的震害进行了详细现场调查， 发现不同场地上的建筑物震害差异很大， 认为震害的严重程度取决于地表的地质特征， 地表为坚固岩石的地区受到的震害较轻， 而地表为人工建筑土层的地区则受到的震害较重． 此后， 对于场地效应的定量研究逐渐展开， 依据所采用资料的不同， 提出了如下几类研究方法： ① 土层反应分析方法． 依据场地土层剪切波速度结构及不同土层密度和动三轴实验数据， 用于假想基岩面以上的局部土层场地的地震反应分析模拟计算（Martin, Seed， 1978； 廖振鹏， 1989； 李小军， 1992）． 该方法适用于局部地表覆盖土层较浅的场地地震反应研究， 其精度较高， 但资料获取的成本也较高． ② 基于钻孔强震记录的参考台法． Borcherdt（1970）基于核爆和强震记录， 提出用场地观测点和附近基岩露头的参考点二者地震记录的频谱之比来计算场地响应经验传递函数的“参考台法”． 对于一般的研究场地， 如果在钻孔内安放强震仪获得不同深度的强震记录， 可以直接利用地表观测记录的傅里叶谱与下部基岩观测记录的谱的比值确定场地效应（Abercrombie， 1997； Satohetal， 1997）． 这种方法简单可靠， 但是资料获取比较困难， 且受到强震记录的局限． ③ 基于场地微震记录的谱比法． Nakamura（1989）进一步利用深井微震实验证明在井下基岩处水平分量与垂直分量频谱几乎相等, 且沉积场地与基岩处的垂直分量频谱也近似相等， 提出了不需要基岩参考面而直接计算沉积场地地震波水平分量与垂直分量频谱比来评估场地响应的单台H/V谱比法． Lermo和Chávez-García（1993）分析了处于墨西哥不同城市的3个场地的传递函数， 断定在简单地质条件的情况下， 卓越周期和局部放大水平可以通过H/V方法估计． Mucciarelli等（2003）综合对比了大量不同振幅的人工噪声振动数据和不同震级的地震数据， 对该方法的稳定性进行了分析和验证， 认为通过不同数据获得的场地响应在峰值频率与放大倍数上具有一致性． 陈棋福等（2009）应用该方法研究北京城区的场地响应， 并在钻孔资料的参考约束下得到了北京城区的沉积盖层厚度分布． ④ 基于场地地震记录的反演方法． 地震记录包含了震源、 地震波传播途径及场地响应等特征． 这类方法旨在区分记录中的震源效应、 传播途径及场地响应， 实现分别反演． Moya等（2000）利用日本神户大地震余震记录， 基于Brune（1970）提出的震源模型， 采用遗传算法实现对场地响应的反演． 黄玉龙等（2003）、 刘杰等（2003）分别利用不同地区的台网记录， 将Atkinson和Mereu（1992）的三段式衰减模型与Moya等（2000）的方法结合， 实现了对Q值、 震源参数、 台站场地响应三者的联合反演． 章文波等（2001）利用唐山近场强震记录， 分析比较了反演法与传统的方法， 认为每种方法都能给出土层的峰值频率， 但是反演法和参考台法获得的场地效应与H/V谱比法获得的场地效应差异较大． 场地效应的另一类问题是振动随距离的衰减． 早期主要基于波动理论对衰减模型进行构建， Bornitz（1931）综合考虑了振动的几何衰减和介质吸收衰减， 提出了半无限空间表面上作用扰力时地面振动振幅的衰减公式， 成为以后一段时间预测地面振动衰减常用的计算公式．

近年来日益凸显的地铁振动已成为城市环境中的重要问题之一． 在地铁振动问题研究中， 由于影响振动的因素较多， 且不稳定体、 实际场地条件往往十分复杂， 要求理论研究与现场观测对比更紧密的结合， 从而使观测成为了重要的研究手段． 通过对列车振动的现场实测， 研究人员总结并发展了不同条件下振级随观测点距轨道距离的经验衰减公式（Kurzweil， 1979； Verhas， 1979a, b； Kurzweil, Ungar， 1982）． 针对城市地区的地铁振动， Nelson和Saurenman（1983）在美国麻省城市运输局的资助下， 系统总结了北美地铁系统各种影响环境振动的因素， 并对各影响因素进行修正， 同时结合一些分析模式， 预测各因素变化带来的影响， 给出了定性和定量两种预测方法， 分别用于不同场合． 日本科研人员也分别在市区地铁周边展开观测， 分别就列车引起的结构振动发生机理、 振动在地下和地面的传播规律以及对周围居民的影响进行研究， 提出了周围环境振动水平的预测方法（Fujikake， 1986； Hayakawaetal， 1992）． 国内科研人员综合观测结果， 并吸取前人经验对Bornitz （1931）的衰减公式进行了修正（茅玉泉， 1987； 杨先键， 2002）， 其成果已列入我国的《动力机器基础设计规范》中， 以对生产建设活动进行指导．

地铁振动是一种与基岩无关、 主要在土层中传播且相对较弱的振动， 没有地震问题中的大应变、 非线性和瞬态场地破坏效应， 但其持久、 近于稳态的振动干扰往往引起地铁沿线附近局部场地的放大效应， 成为地铁环境振动问题中的主要因素． 本文利用北京地铁4号线北京大学东门站附近地铁隧道壁和场地的振动观测数据， 通过反复研究分析， 发现并提出一种基于信号独立条件的谱时程比方法， 能从地铁振动数据中提取到非常稳定的场地土层放大效应的特征信息． 该方法利用地铁隧道壁观测数据和地面场地观测点数据， 通过一种时间—频率—时间的变换， 建立不同频率振动方均根谱随时间的变化曲线， 同时基于地铁振源与地面交通振源在空间位置、 振动过程和形成机制等方面的相互独立条件， 通过互相关分析， 获得表征场地土层对某些振动频率的“衰减”或“放大”的滤波作用. 其与特定场地条件下的受迫共振效应相关联． 通过对同一观测点不同时间段的振动数据分析发现， 所获得的地层放大效应的峰值频率等特征参数具有高度的稳定性， 与具体的振动绝对值和观测时间无关． 同时， 对百米范围内5个不同观测点振动数据的分析表明， 每一个观测点的地层放大效应随频率变化的特征存在局部差异， 与各个观测点具体的地层分层结构特征关系密切． 结合北京大学东门附近3个钻孔剖面数据， 将距离钻孔最近3个测点的上述分析结果与按经典半无限空间分层介质建立的传递函数进行比较， 表明由本方法通过实测振动数据获得的结果在峰值频率及放大效应随频率变化的趋势与传递函数曲线都具有较强的一致性． 在此基础上， 本文进一步针对地层的近场振动衰减进行分析， 给出了近地表土层的振动等效衰减系数．

1 基于谱时程比方法的地层振动响应信息提取

2012年9—10月， 北京大学环境振动监测与评估实验室与中国电子研究院防微振研究所分别对北京地铁4号线北京大学东门站附近地铁及其周围的环境振动进行联合观测对比研究， 以了解地铁4号线附近的环境振动及其衰减特征．

观测点分布如图1所示． 其中地面观测点13个， 编号从1—13， 位于北京大学东门附近校园内， 分布在大约相距100 m的南、 北两条测线上． 各测点与地铁4号线的垂直距离为50—300 m． 所有测点布设于第四纪原状土层的竖井内， 高程相同， 其中7号和9号测点紧邻北京大学生命科学学院大楼地基， 其它测点附近没有永久性建筑物． 同时在地铁内布设两个测点， 编号为200和201， 分别位于地铁上行和下行的隧道内侧壁的中点上， 距离地面的深度约12 m． 所有测点采用24小时连续观测方式， 采样频率均为200 Hz． 地面观测仪器型号为VSE-355G3， 地铁内的观测仪器型号为CV374， 均由东京测震制造．

图1 观测点分布图

由于仪器数量的限制， 地面13个观测点先后分3个时间段完成． 本文只选用了地表3号、 7号、 8号、 9号和10号等5个测点与地铁下行隧道上的200号测点观测时间同步的部分振动观测数据． 各测点与地铁线的垂直距离由近及远依次为7号、 8号、 9号、 3号和10号．

测试场地东侧有交通流量比较大的中关村北大街， 其下部是正在运营的北京地铁4号线． 图2给出了2012年9月28日7:20—7:30分别在地铁隧道内200号测点和地面8号测点获得的一组长达10分钟的时间域观测记录． 可以看出： 在同一时间段两个观测点数据有某些相似之处， 如某些峰值出现的时间相同； 同时也存在较大差异， 地面测点出现的时间峰值个数远远多于地铁隧道内． 这是因为， 地铁隧道内的观测记录主要反映了地铁引起的振动， 而地面观测记录不仅包含地铁引起的振动， 也包含地面交通振动和场地附近其它随机振源产生的振动．

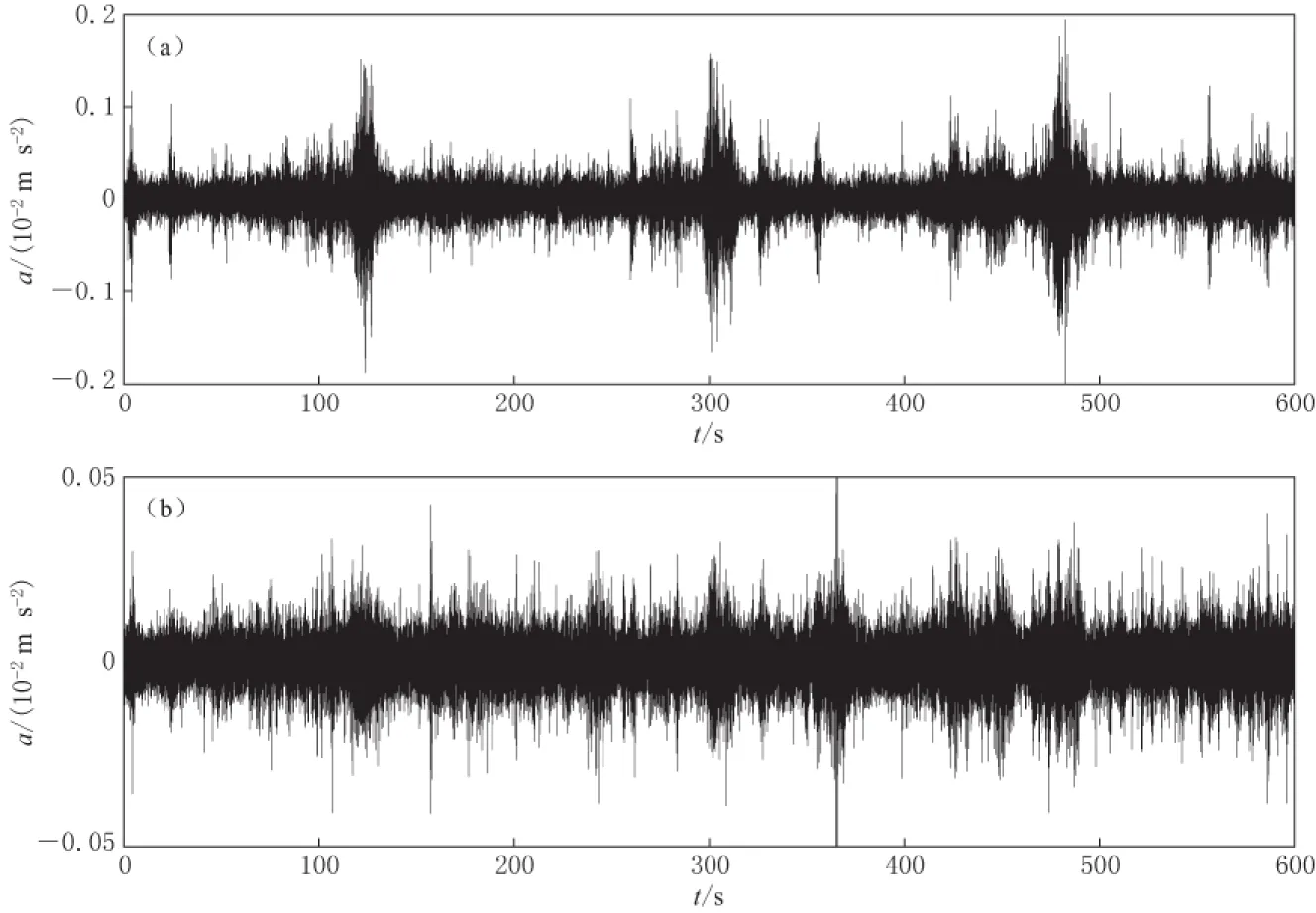
图2 2012年9月28日7:20—7:30观测记录（南北向加速度振动记录）

本文在对上述相同时间段来自地面和地下两种不同信号的分离研究过程中发现采用一种新的时-频分析技术可以从地铁振动和地面环境振动观测数据中提取到非常稳定的浅表地层振动响应曲线和相应的峰值频率． 其方法如下：

设A（t）为地面测点记录到的振动，B（t）为地铁隧道壁上记录到的振动，C（t）为未知的以地面交通为主的其它干扰振动． 因此， 地面记录信号A（t）包含了地铁振动B（t）经过介质传播到达测点的信号以及以路面交通为主的其它干扰C（t）在测点引起的振动． 由此可将A（t）表示为

A（t）=αB（t）+C（t），

（1）

式中，α等于地铁振动振幅与其经过传播介质到达测试场地时的振幅之比． 由于传播介质对振动的放大或吸收随频率而变化， 因此α与振动频率相关． 基于地铁振源与路面交通振源在其空间位置、 振动过程和形成机制等方面的显著差异， 如果假设振动B（t）与C（t）的时间过程相互独立， 则可采取下列表达式来确定α：

α={α:R（A（t）-αB（t）,B（t））=0},

（2）

即α的取值为从振动A（t）中去掉合适比例的振动B（t）之后的剩余振动信号， 而与振动信号B（t）不相关． 式（2）中，R代表两组随机信号之间的互相关函数， 若随机信号记为x和y， 且均为包含N个点的时间序列， 则互相关函数R（x,y）的表达式为

（3）

式（2）中， 当信号A（t）-αB（t）与信号B（t）无关， 则当R=0时可求得相应的振幅比系数α． 设A（t）和B（t）都是N点的时间序列， 表示为A（ti）和B（ti）. 通过式（3）并结合式（2）给出的条件， 即可求出α为

.

（4）

考虑到振幅比α随频率变化， 需要对观测振动数据进行频率分析． 为此， 选用工程中最常用的1/3倍频程谱来描述振动幅值， 可更充分地反映振动在某个频率点附近区间上的平均有效强度． 对于某中心频率f， 按照1/3倍频程的分段标准， 其带通滤波频段为

（2-1/6f, 21/6f）.

（5）

具体来说， 对于一组相同时间段的地面记录信号A（t）和地铁振动信号B（t）分别按一定时间间隔Δt进行截断， 再按不同中心频率滤波后得到相应的1/3倍频程方均根谱． 若干个相连Δt的计算结果就构成了信号A（t）和B（t）随时间变化的“谱时程”曲线SA（f,t）和SB（f,t）. 图3给出了地下200号观测点和地面8号观测点早7:20的数据在中心频率f=10.0 Hz的频率段所求取的“谱时程”曲线， 每一个点表示对应时刻附近Δt=4 s时间间隔内振动（加速度）的方均根值． 将二者的“谱时程”曲线SA（f,t）和SB（f,t）作为时间序列替代A（t）和B（t）， 利用式（4）可以确定该中心频率f所对应的振幅比系数α值， 即

.

（6）

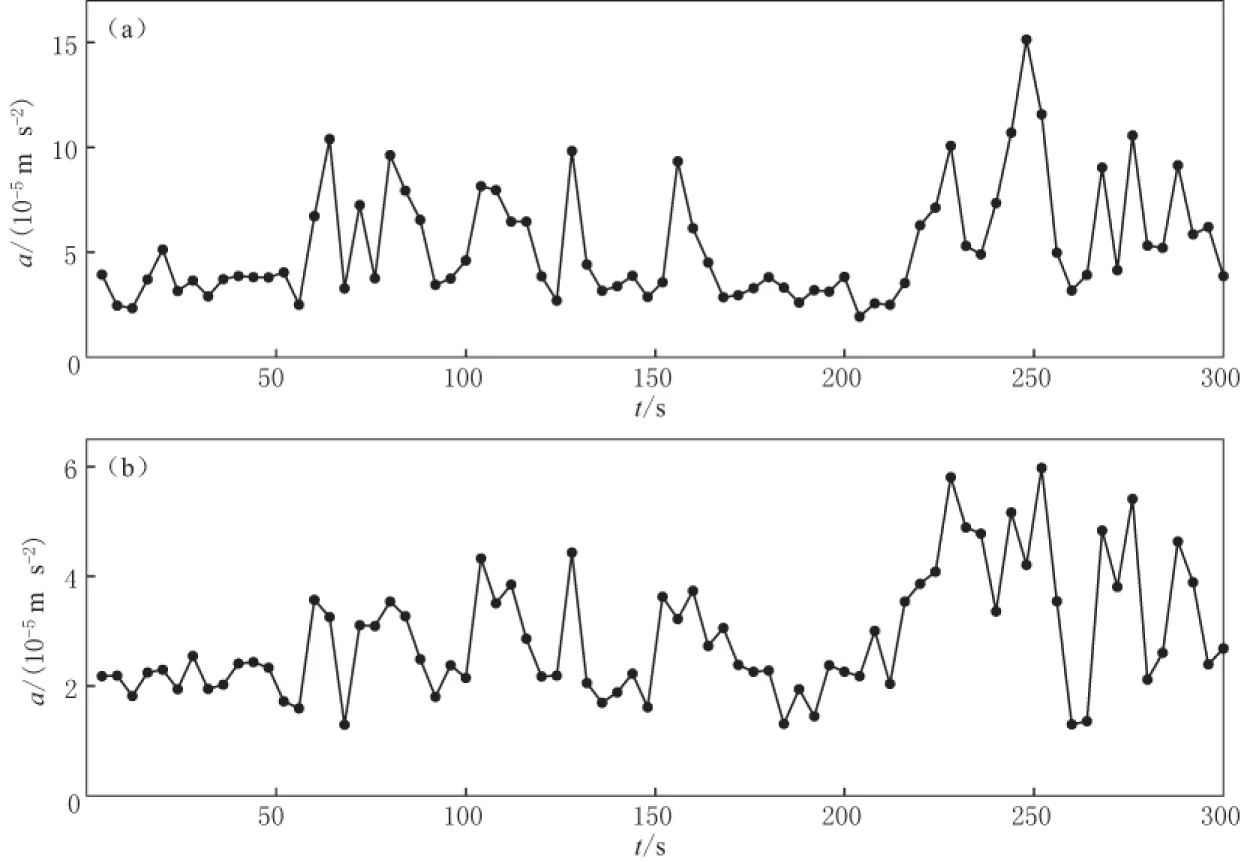
图3 10.0 Hz “谱时程”曲线（时间间隔为4 s）

不同中心频率对应的“谱时程”曲线各不相同， 改变中心频率即可确定α随振动频率的变化曲线α（f）, 简称振幅比频率曲线． 由于观测场地获得的地铁振动和地面交通振动主要集中在1.0—25.0 Hz， 故本文中按0.2 Hz的频率间隔在1.0—25.0 Hz频率范围对f作等间隔连续取值来获得α（f）曲线．

本文计算“谱时程”曲线时， 是将每一天不同时间段内的数据按5—10分钟时间长度分组， 同时Δt取为4 s， 这是一个经验值， 与一次地铁制动或启动过程持续时间相近．

图4给出了地铁运营期间8号测点南北分量多个时间段数据的α（f）频率变化曲线. 图中显示这些随机选取的来自不同时间段的α（f）结果具有较好的一致性， 并显示α（f）曲线在接近10 Hz频率有一个明显的峰值， 在5 Hz附近也有局部的极大值．

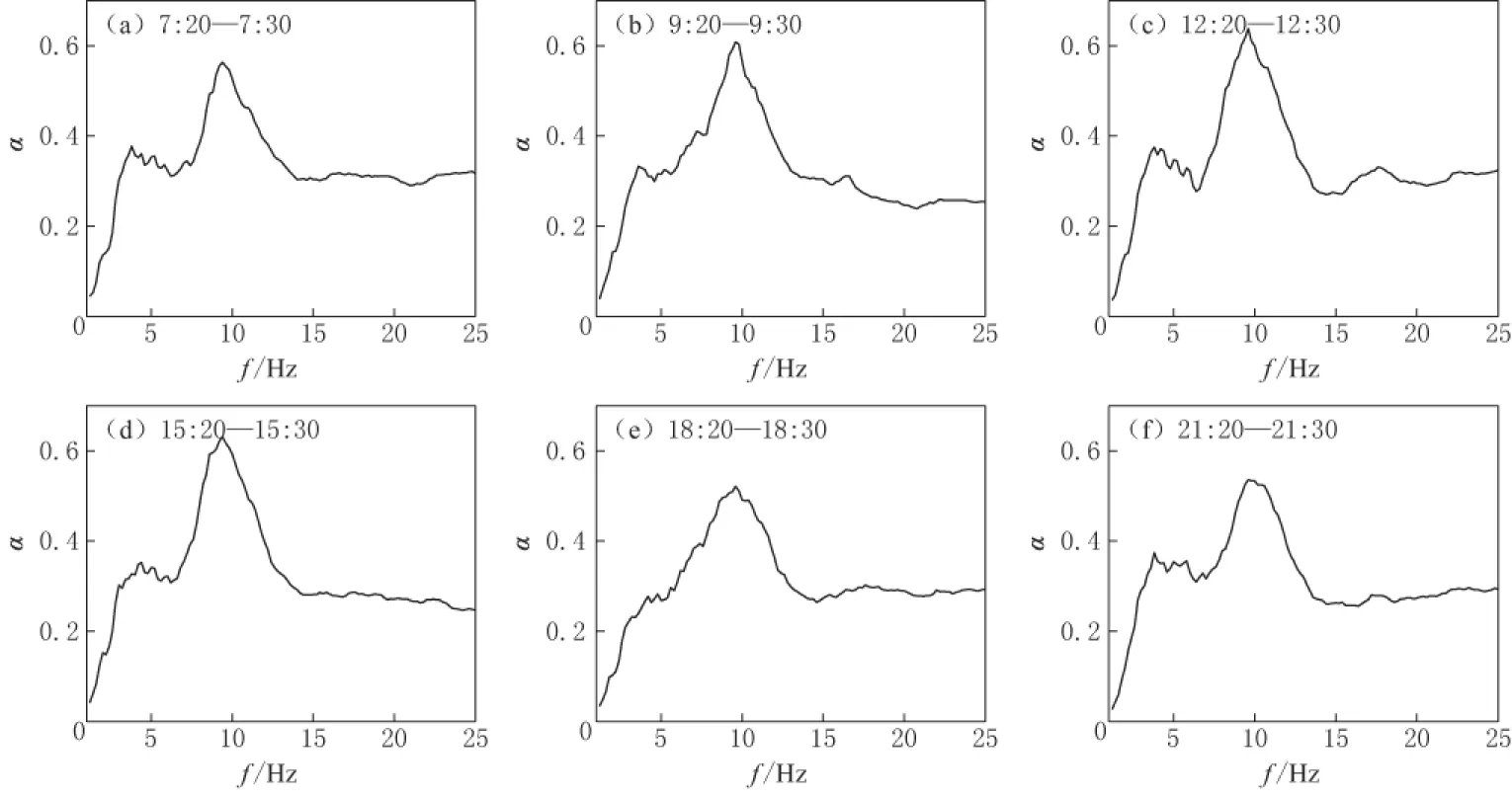
图4 8号观测点南北分量不同时间段振幅比频率曲线计算结果

研究结果表明， 除8号测点南北分量外其垂直和东西分量以及其它测点的各个分量数据也有类似的结果． 图5给出了所有5个测点三分量的α（f）计算结果. 图中从上到下依次按照测点与地铁线的垂直距离由近及远排列. 其中每个子图中分别包括一天中6:00—22:00内不同时间段对应的16组结果．

这些结果表明： ①α（f）与时间选取无关， 表明在地铁及周边振动源作用下场地地层对振动的某种固有放大效应. ② 不同测点同一分量α（f）随频率变化的趋势接近， 其在南北分量上尤为突出， 应该与地铁在测试场地附近的南北走向相关． ③ 不同测点α（f）所反映的放大效应的峰值频率关系存在一定的差异， 可能与测点具体所在场地的局部地质条件有关． 所有结果总体上表明： 放大效应主要的峰值频率在3—10 Hz， 其它频率成分受到场地放大的效应都不显著； 单一组α（f）曲线可能包括多个峰值频率． 其中， 各测点南北分量的放大效应表现为“双峰”或“三峰”特征， 主要峰值频率在4 Hz和10 Hz附近． 不同的是7号和9号两个测点东西和垂直两个分量的场地响应特征明显区别于其它测点， 其原因可能与7号和9号两个测点紧邻北京大学生命科学学院大楼有关． 通常， 建筑物的存在会在一定程度上改变场地原有的振动特征． 此外， 各测点南北分量的振动放大强度显著高于东西分量和垂直分量， 进一步说明了地铁运行方向振动的特殊性． 其它地区的观测也显示了地铁行进方向的地面振动在原始时间域的记录上为最大， 在某种程度上揭示了地铁运行引起的振动对其附近地面环境振动的主导和控制作用．

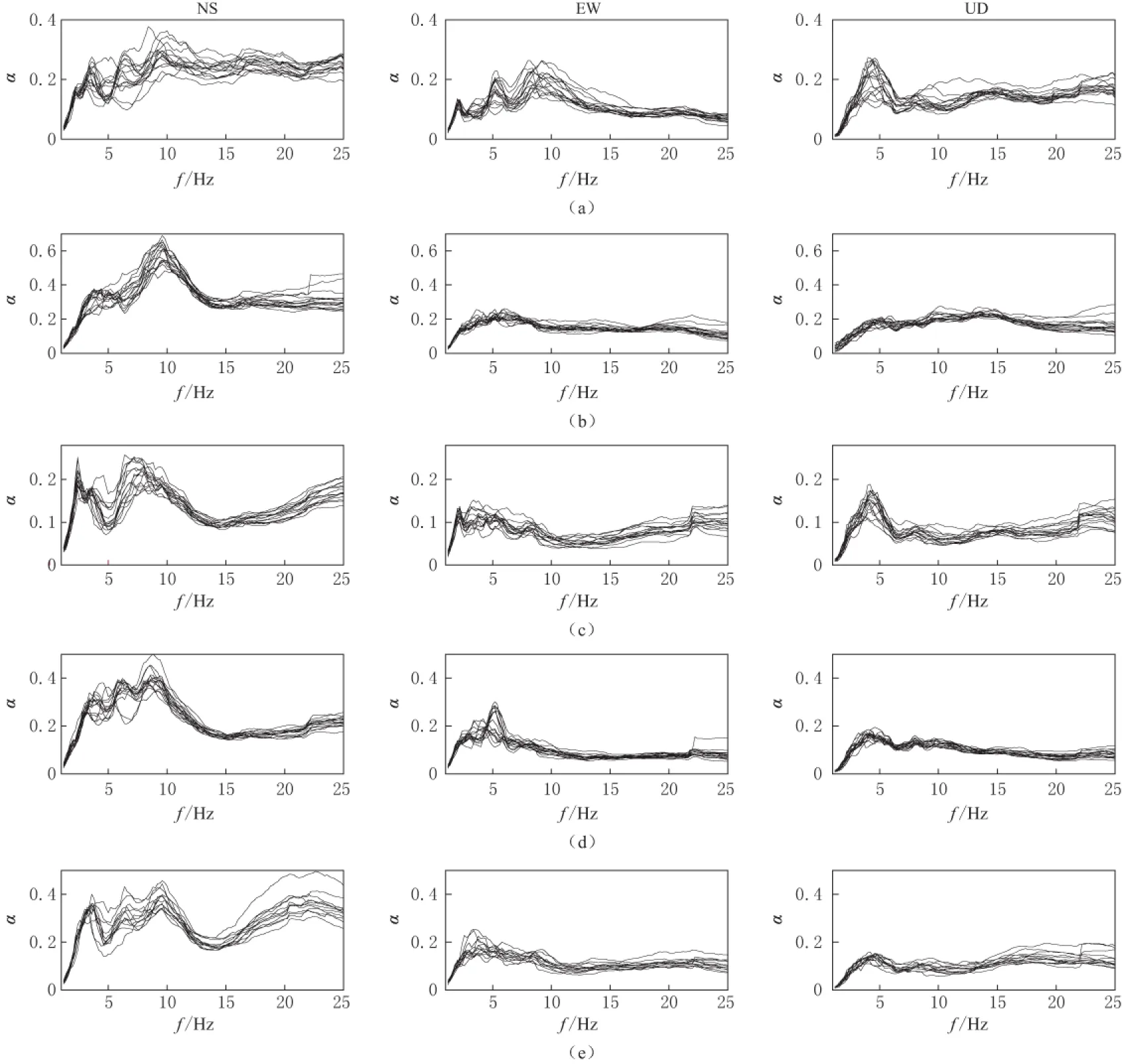
图5 各观测点各分量实测振幅比频率曲线

Fig.5 Measured amplitude ratio-frequency curves for three components of all stations

（a） 7号观测点； （b） 8号观测点； （c） 9号观测点； （d） 3号观测点； （e） 10号观测点

（a） Station No.7; （b） Station No.8; （c） Station No.9; （d） Station No.3; （e） Station No.10

2 振幅比频率曲线与场地理论传递函数的对比

如前所述， 振幅比频率曲线α（f）代表了测点所在位置场地固有的振动响应特性． 如果这样，α（f）应该与场地的理论传递函数有关． 为此， 本文进行了验证和对比， 进一步了解两者的关系．

众所周知， 半无限空间分层介质模型的传递函数H（f）完全由观测点附近的土层参数决定． 参照廖振鹏（2002）给出的半无限空间分层介质、 平面剪切波从基岩垂直入射的稳态波动传递函数， 相邻两层之间振幅的关系可表示为

（7）

式中：En和Fn分别表示从地表向下第n层介质中的上行波和下行波的振幅；Tn为表示第n层与第n+1层之间上、 下行波振幅关系的传递矩阵， 可由相邻两层的土层厚度h、 密度ρ和剪切波波速v表示， 也与频率f有关． 若模型为N层土层模型， 第N+1层为基岩， 则稳态剪切波从基岩入射时顶层振幅与基岩振幅的关系可表示为

（8）

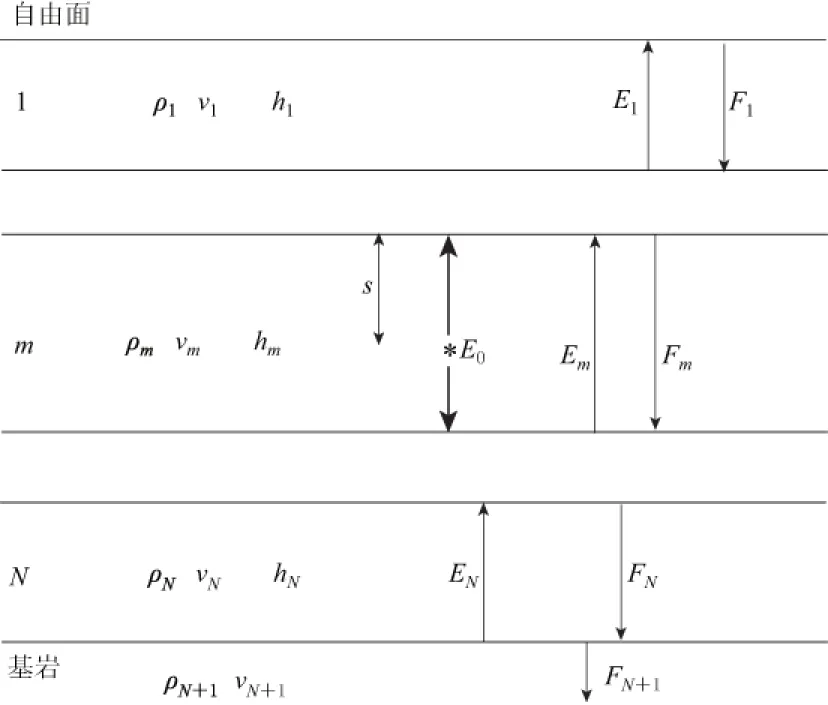
图6 半无限空间分层介质模型示意图

与该模型略有不同， 本文面临的问题中振动来自于土层中部（地铁所在位置）， 而不是底部基岩． 为此， 须首先对基岩入射场地理论传递函数进行适当的修正．

如图6所示， 对于N层介质模型， 设第N+1层为基岩， 振源处于第m层中， 相对深度为s． 需要说明的是，Em和Fm分别为第m层中的透射和反射振动， 而不包括振源的振动．

设E0为振源的振幅， 则第m层振源振动在上下界面的振幅需用E0分别乘以因子e-ikms和e-ikm（hm-s）． 其中：km=ω/vm为第m层中的剪切波波数；ω=2πf为圆频率． 类似地， 仿式（7）、 （8）， 根据波的反射透射理论， 可以分别导出第m层下方各层与上方各层波幅的传递关系为

（9）

（10）

记

（11）

Td和Tu分别为振源下方和上方振幅的总传递矩阵． 结合自由表面的边界条件E1=F1， 以及EN+1=0， 联立式（9）、 （10）和（11）， 得到地表处的振幅U为

（12）

其中， 传递函数为

（13）

特别是当振源处于第一层时，Tu为单位矩阵， 传递函数可以简化为

（14）

上述传递函数都是在线弹性介质假设下得到的． 对于地铁振源等环境振动条件下， 即使假设土层处于小应变情况， 其非完全弹性对振动的吸收衰减也难以简单忽略． 对此， 如果用阻尼来近似， 可将上面各式中的波速表示为等效波速， 即

（15）

传递函数的幅值表示地表振动与振源振动振幅的比例关系以及随频率的变化关系． 传递函数与土层的分层、 厚度、 速度结构密切相关（窦立军， 杨柏坡， 2001）． 下面根据场地附近的钻孔数据， 用式（13）计算理论传递函数并与通过“谱时程”方法得到的振幅比频率曲线实测结果进行比较．

3号、 8号、 10号测点附近50 m范围内存在的3个钻孔剖面， 显示出在该地区土层地下1—4 m深主要以人工填土为主， 土质较软、 波速较低； 地下约20 m处是黏土层与砾石层的分界， 波速从150 m/s跃变到250 m/s； 而20 m以下的砾石层剪切波波速达到450 m/s左右， 可以认为地铁振动在该层以下的反射波比较弱． 表1给出了土层中各分层的剪切波速度、 密度和介质阻尼比参数．

表1 钻孔剖面土层参数Table 1 Soil parameters in boreholes

本文计算中， 将地铁振源深度设为12.5 m， 这大致是地铁隧道中心的深度． 理论计算表明， 3—10 Hz的峰值频率主要由地下20 m左右的介质分界面引起． 表2给出了不同钻孔剖面土层分层界面深度、 不同测点实测和理论峰值频率及振幅比值（对于多个峰值频率的情形， 给出最高峰值处的对应频率）． 可以看出， 通过“谱时程”方法得到的实测峰值频率与传递函数理论得到的峰值频率十分接近， 但与峰值频率对应的振幅比相差约3—4倍． 传递函数得到的振幅比反映了场地对振动的放大特征， 而实测的峰值振幅比仅为0.3—0.6， 其原因与地铁的振动观测有关． 地铁隧道壁的振动观测位置处于隧道内侧壁中点， 因此所

表2 不同测点选取土层的深度及理论与实测结果比较Table 2 Depths of soil layers and comparison between theoretical and measured results for different stations

观测到的振动能很好地反映地铁产生的振动强度和时间过程， 但却不能简单等价于隧道外侧壁附近同一深度土层的振动， 至少其振动幅度存在差异． 因为， 隧道壁与周围土层的振动耦合一定程度上会对振动的强度起到调制作用． 这种耦合很可能存在非线性过程， 也许不能用简单的反射、 透射阻抗来评估． 由于理论传递函数与本文通过振动观测数据获得的实测振幅比频率曲线变化关系十分接近（图7）， 几乎只是相差一个比值常数. 作为一种简化处理， 本文在后面将上述振动耦合对振幅的调制以及介质其它衰减作用用一个与频率无关的常数η来描述． 图7给出了通过振动观测数据获得的振幅比频率曲线与理论传递函数曲线的对比结果．

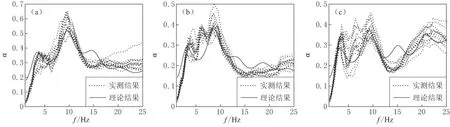
图7 实测振幅比频率曲线与理论传递函数曲线对比（南北分量）

从表2和图7的结果可以看出， 本文提出的“谱时程”方法所得到的场地放大效应峰值频率和振动响应随频率变化的趋势都与依据钻孔资料得到的理论传递函数十分接近． 由此可见， 本文提出的谱时程比数据处理方法可以得到比较准确的场地放大效应特征． 因此， 在缺少钻孔资料的条件下可以用于对测点附近场地的放大效应特征进行实测分析． 事实上， 理论传递函数是在对介质特性作某些简化近似的条件下获得的， 其误差影响因素较多， 且不易被确定和估计． 同时， 对于环境复杂的场地， 如有大型地面建筑物和地下结构体存在的情况， 单独依赖钻孔剖面数据建立的简单土层模型所获得的理论传递函数难以准确地反映场地的实际振动特征． 这时， 实测的方法更具有价值． 这一点从图7的某些细节中可进一步得到验证． 事实上， 图7中实测曲线虽然大体走势与理论的传递函数曲线对应， 但是在个别细节处仍然会有偏差． 例如： 实测的3号、 10号测点在6 Hz附近均有峰值， 而理论曲线却是一个谷值； 8号、 10号测点的15 Hz处也有趋势上的差别． 如前所述， 理论传递函数的幅值受模型参数细节的影响较大， 而实际的地层结构比简单的两层模型要复杂得多． 由于地下可能存在着厚度不一的各种坚硬、 软弱层， 而且场地周围也存在着各种不同的环境因素， 其共同作用可能会导致次生峰值的出现．

3 振动衰减综合特征分析

如前所述， 由于地铁振动观测地点的限制， 尽管理论传递函数与实测振幅比频率曲线在变化趋势和峰值频率点十分接近， 但各自的强度幅值存在显著差异． 显然， 导致实测α（f）较小的原因不仅可能包含了隧道壁与隧道外部土层的振动耦合效应， 同时也包含了振动在非完全弹性土层中传播的衰减效应． 由于缺乏更详细的隧道和土动力学资料， 本文将这一问题笼统地综合为“衰减”来考虑． 如果假设由于实测α（f）与理论传递函数H（f）的幅值呈正相关， 则存在一个与频率无关的衰减系数η使成立. 研究中用大量实测数据对α（f）与H（f）进行最小残差拟合来获得η， 其结果见表3． 可以看出， 本研究区域中距离地铁线路100—200 m范围内的η值在0.1—0.15之间．

α（f）=η|H（f）|

（16）

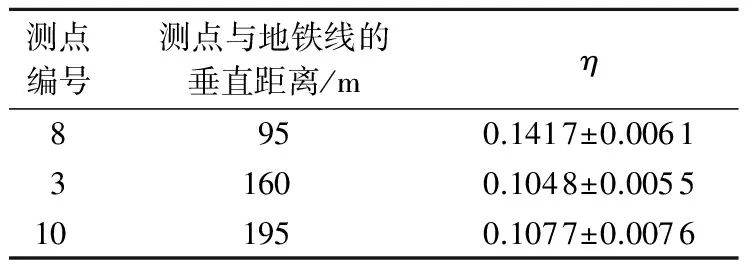
表3 不同测点与地铁线的垂直距离及衰减系数拟合结果Table 3 Distances perpendicular to subway line and fitting results of attenuation coefficients for different stations

既然η反映的是某种“综合衰减”， 就应该与距离有关． 由于较难严格区分隧道壁-土层耦合效应与土层非线性吸收效应， 以及考虑本文所有测点与地铁关系构成的近场情况， 假设η与距离R之间存在如下单值函数关系：

η=kR-m，

（17）

式中k为比例系数． 对式（17）两边分别取对数， 得

lgη=lgk-mlgR.

（18）

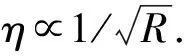
4 讨论与结论

本文基于隧道内地铁振动数据与地面振动数据的“谱时程”的独立无关性假设， 提出一种新的时间-频率数据处理方法， 从而可直接通过对地铁振动与地面振动数据的对比获取观测点附近场地的放大效应和衰减特征信息， 并得出以下结论：

1） 将本文提出的“谱时程”方法应用到振动观测数据中， 所获得的同一位置不同时间的振幅比频率曲线结果具有高度的稳定性和一致性， 是一种从观测数据中提取地层振动响应和传播介质信息的有效方法．

2） 依据研究区域钻孔资料提供的地层参数， 对地铁振源条件下的理论传递函数曲线与通过本文方法获得的振幅比频率曲线对比结果显示， 理论传递函数曲线与振幅比频率曲线所揭示的场地响应的特征频率一致， 且传递函数曲线与振幅比曲线随频率变化的趋势吻合， 因而本文提出的方法可以对测点附近场地的放大效应进行有效的分析．

3） 实际数据分析结果表明， 北京大学东门附近地铁振动场地响应的峰值频率主要为3—10 Hz； 不同测点、 不同分量之间场地放大效应的特征存在微小差异， 不仅反映了测点局部场地条件的差异， 也揭示了地铁对其周围地面环境振动的主导和控制作用．

4） 基于对隧道-土层耦合和土层非线性振动吸收产生的振动衰减作用的简单假设， 获得了表征衰减平均特征的等效衰减系数， 并在极近场的条件下近似得到了等效衰减系数与相距地铁距离的1/2次方成反比的关系. 该关系与振动在近场的几何扩散规律相近． 但由于各种复杂因素和数据量较少的影响， 其结果有待更多研究的检验．

作者对中国地震局陈运泰院士、 姚陈研究员、 北京大学地质系刘锡大教授、 地球物理系王彦宾教授对本文给予的指导， 北京市快轨建设管理委员会、 北京大学环境振动监测与评估实验室给予的大力支持， 以及周思杰、 焦敬悦对本研究建设性论断的启发表示感谢． 本文的土层模型参数参照了北京市地震工程勘察院《北京地铁四号线工程成府路站岩土工程勘察报告》以及中航勘察设计研究院有限公司《“海淀山后线对北京大学精密仪器实验楼振动影响综合解决方案”科研项目（地铁4号线部分）岩土工程咨询报告》， 在此表示感谢．

陈棋福, 刘澜波, 王伟君, Rohrbach E. 2009. 利用地脉动探测北京城区的地震动场地响应[J]. 科学通报, 53（18）: 2229--2235.

Chen Q F, Liu L B, Wang W J, Rohrbach E. 2009. Site effects on earthquake ground motion based on microtremor measurements for metropolitan Beijing[J].ChineseScienceBulletin, 54（2）: 280--287.

窦立军, 杨柏坡. 2001. 场地条件对传递函数的影响[J]. 建筑科学, 17（3）: 40--46.

Dou L J, Yang B P. 2001. Influence of site conditions on transfer function[J].BuildingScience, 17（3）: 40--46 （in Chinese）.

黄玉龙, 郑斯华, 刘杰, 赵兴权, 康英. 2003. 广东地区地震动衰减和场地响应的研究[J]. 地球物理学报, 46（1）: 54--61.

Huang Y L, Zheng S H, Liu J, Zhao X Q, Kang Y. 2003. Attenuation of ground motion and site response in Guangdong region[J].ChineseJournalofGeophysics, 46（1）: 54--61 （in Chinese）.

雷军, 张志强, 赵长海, 张宇, 马筱月, 程乾, 冯力理. 2010. 北京4号地铁线通车前后北京大学东门环境振动的比较研究[C]∥中国地球物理2010: 中国地球物理学会第二十六届年会、 中国地震学会第十三次学术大会论文集. 北京: 中国地球物理学会、 中国地震学会: 758.

Lei J, Zhang Z Q, Zhao C H, Zhang Y, Ma X Y, Cheng Q, Feng L L. 2010. The environmental vibration comparative study of the east gate of Peking University before and after Beijing metro line 4 open to traffic[C]∥ChineseGeophysics2010:ChineseGeophysicalSociety26thAnnualConference,SeismologicalSocietyofChina13thAcademicConferenceProceedings. Beijing: Chinese Geophysical Society, Seismological Society of China: 758 （in Chinese）.

雷军, 张志强, 张献兵, 王博, 蒋生淼, 张琼. 2013. 北京地区地铁振动衰减特征研究[C]∥中国地球物理2013: 第二十四分会场论文集. 北京: 中国地球物理学会: 117.

Lei J, Zhang Z Q, Zhang X B, Wang B, Jiang S M, Zhang Q. 2013. Subway vibration attenuation characteristic research of Beijing area[C]∥ChineseGeophysics2013:The24thSessionProceedings. Beijing: Chinese Geophysical Society: 117 （in Chinese）.

李小军. 1992. 场地土层对地震地面运动影响的分析方法[J]. 世界地震工程, 8（2）: 49--60.

Li X J. 1992. Analysis method for effects of soil layer on earthquake ground motion[J].WorldEarthquakeEngineering, 8（2）: 49--60 （in Chinese）.

廖振鹏. 1989. 地震小区划: 理论与实践[M]. 北京: 地震出版社: 141--153.

Liao Z P. 1989.SeismicMicrozonation:TheoryandPractice[M]. Beijing: Seismological Press: 141--153 （in Chinese）.

廖振鹏. 2002. 工程波动理论导引[M]. 第二版. 北京: 科学出版社: 44--53.

Liao Z P. 2002.IntroductiontoWaveMotionTheoriesinEngineering[M]. 2nd ed. Beijing: Science Press: 44--53 （in Chinese）.

刘杰, 郑斯华, 黄玉龙. 2003. 利用遗传算法反演非弹性衰减系数、 震源参数和场地响应[J]. 地震学报, 25（2）: 211--218.

Liu J, Zheng S H, Huang Y L. 2003. The inversion of non-elasticity coefficient, source parameters, site response using genetic algorithms[J].ActaSeismologicaSinica, 25（2）: 211--218 （in Chinese）.

茅玉泉. 1987. 交通运输车辆引起的地面振动特性和衰减[J]. 建筑结构学报, 8（1）: 66--77.

Mao Y Q. 1987. Characteristics and attenuation of ground vibration caused by traffic vehicle[J].JournalofBuildingStructures, 8（1）: 67--77 （in Chinese）.

杨先键. 2002. 人为地面振动的传播与衰减[C]∥首届环境岩土工程学术交流会论文集. 上海: 同济大学出版社: 35--41.

Yang X J. 2002. Man-made ground vibration propagation and attenuation[C]∥ProceedingoftheFirstEnvironmentalGeotechnologySymposium. Shanghai: Tongji University Press: 35--41 （in Chinese）.

章文波, 谢礼立, 郭明珠. 2001. 利用强震记录分析场地的地震反应[J]. 地震学报, 23（6）: 604--614.

Zhang W B, Xie L L, Guo M Z. 2001. Estimation on site-amplification from different methods using strong motion data obtained in Tangshan, China[J].ActaSeismologicaSinica, 23（6）: 604--614 （in Chinese）.

Abercrombie R E. 1997. Near-surface attenuation and site effects from comparison of surface and deep borehole recordings[J].BullSeismolSocAm, 87（3）: 731--744.

Atkinson G M, Mereu R F. 1992. The shape of ground motion attenuation curves in southeastern Canada[J].BullSeismolSocAm, 82（5）: 2014--2031.

Borcherdt R D. 1970. Effects of local geology on ground motion near San Francisco Bay[J].BullSeismolSocAm, 60（1）: 29--61.

Bornitz G. 1931.ExpansionofHeavyDrillingProducingGroundMotionintheDeep[M]. Berlin: Springer: 44 （in Germany）.

Brune J N. 1970. Tectonic stress and the spectra of seismic shear waves from earthquakes[J].JGeophysRes, 75（26）: 4997--5009.

Fujikake T. 1986. A prediction method for the propagation of ground vibration from railway trains[J].JSoundVib, 111（2）: 357--360.

Hayakawa K, Sawatake M, Gotoh R, Matsui T. 1992. Reduction effect of ballast mats and EPS blocks on ground vibration caused by trains and its evaluation[C]∥INTER-NOISEandNOISE-CONCongressandConferenceProceedings. Washington: Institute of Noise Control Engineering, （2）: 593--596.

Kurzweil L G. 1979. Ground-borne noise and vibration from underground rail systems[J].JSoundVib, 66（3）: 363--370.

Kurzweil L G, Ungar E E. 1982. Prediction of noise and vibration in buildings near the New York City subway[C]∥INTER-NOISEandNOISE-CONCongressandConferenceProceedings. Washington: Institute of Noise Control Engineering, （2）: 213--216.

Lermo J, Chávez-García F J. 1993. Site effect evaluation using spectral ratios with only one station[J].BullSeismolSocAm, 83（5）: 1574--1594.

Martin P P, Seed H B. 1978.MASH:AComputerProgramfortheNon-LinearAnalysisofVerticallyPropagatingShearWavesinHorizontallyLayeredDeposits[CP]. Berkeley: Earthquake Engineering Research Center, University of California: 93.

Moya A, Aguirre J, Irikura K. 2000. Inversion of source parameters and site effects from strong ground motion records using genetic algorithms[J].BullSeismolSocAm, 90（4）: 977--992.

Mucciarelli M, Gallipoli M R, Arcieri M. 2003. The stability of the horizontal-to-vertical spectral ratio of triggered noise and earthquake recordings[J].BullSeismolSocAm, 93（3）: 1407--1412.

Nakamura Y. 1989. A method for dynamic characteristics estimation of subsurface using microtremor on the ground surface[J].QuarterlyReportofRTRI, 30（1）: 25--33.

Nelson J T, Saurenman H J. 1983.State-of-the-ArtReview:PredictionandControlofGroundborneNoiseandVibrationfromRailTransitTrains[R]. Report No. UMTA-MA-06-0049-83-4. Oakland: Wilson, Ihrig & Associates, Inc., 222.

Satoh T, Kawase H, Sato T. 1997. Statistical spectral model of earthquakes in the eastern Tohoku district, Japan, based on the surface and borehole records observed in Sendai[J].BullSeismolSocAm, 87（2）: 446--462.

Verhas H P. 1979a. Measurement and analysis of train-induced ground vibration[C]∥INTER-NOISEandNOISE-CONCongressandConferenceProceedings. Washington: Institute of Noise Control Engineering, （2）: 726--731.

Verhas H P. 1979b. Prediction of the propagation of train-induced ground vibration[J].JSoundVib, 66（3）: 371--376.

Wood H O. 1908. Distribution of apparent intensity in San Francisco[G]∥CaliforniaEarthquakeofApril18, 1906:ReportoftheStateEarthquakeInvestigationCommission. Washington: Carnegie Institute, Publication 87, 1: 220--246.

Spectrum-time history ratio method and its application to determination of formation site effect near subway line

（SchoolofEarthandSpaceSciences,PekingUniversity,Beijing100871,China）

We deployed seismometers in subway tunnels and on ground in the vicinity of East Gate of Peking University Station of Beijing Subway Line 4. Using the vibration data obtained, we proposed a data processing method based on independent signals, which we called spectrum-time history ratio method, thus we could obtain stratigraphic site effect and the information of vibration attenuation characteristics from subway vibration data and ground vibration data. Vibration data from different time periods in the same observation point are analyzed and calculated. The results are highly stabilized and proved a good consistency with frequency response characteristics of theoretical transfer function applied in layered half-space medium model based on borehole data. Meanwhile, we also evaluated integrated equivalent attenuation characteristics induced by coupled vibration of tunnel wall and the soil and inelastic absorption of upper layers near the observation points based on the method. Our results indicate that the peak frequencies of site amplification effect of vibration range mainly between 3—10 Hz near the East Gate of Peking University Station. Affected by the vibration of the subway, site resonance exhibits a strong dependence on direction and a spatial variation.

subway vibration; site effect; peak frequency; attenuation

10.11939/jass.2015.01.004.

北京市科技计划项目（SHX-QT-YJSY-02）资助.

2014-05-05收到初稿， 2014-05-30决定采用修改稿.

e-mail: wbpku@pku.edu.cn

10.11939/jass.2015.01.004

P315.3+1

A

王博, 雷军. 2015. 谱时程比方法及其在确定地铁沿线地层场地响应中的应用. 地震学报, 37（1）: 39--52.

Wang B, Lei J. 2015. Spectrum-time history ratio method and its application to determination of formation site effect near subway line.ActaSeismologicaSinica, 37（1）: 39--52. doi:10.11939/jass.2015.01.004.