三角形面元分割法计算地球同步卫星视星等

胡　淼,邓　晶，徐国蕊，李齐良，周雪芳，曾　然，魏一振，卢　旸

三角形面元分割法计算地球同步卫星视星等

胡淼,邓晶，徐国蕊，李齐良，周雪芳，曾然，魏一振，卢旸

摘要:为了描述地球同步轨道卫星表面的光学特性，提出了快速三角形面元分割法计算卫星有效反射面积，结合太阳、卫星和观测点三者之间的时空关系，建立目标视星等计算模型。为了验证模型，对在轨地球同步卫星FY-2在不同时刻的有效反射面积和视星等进行仿真。结果表明，与网格化面元分割法对目标表面分割数为1600时达到收敛相比，采用三角形面元的分割数为256时，模型即达到收敛条件。此时，计算得有效反射面积与经验公式计算差值接近10-3，有效降低了面元分割数和模型复杂度。采用光电转台对目标进行跟踪观测实验，当观测时刻为2013年5月1 日19:00-20:00时，目标视星等观测值为12.6~12.8，理论计算视星等与实验结果符合较好。

关键词:地球同步卫星；视星等；三角形面元分割法；有效反射面积；光电跟踪

1引言

空间目标的视星等作为天、地基监测系统的重要指标之一，不仅对空间目标的姿态控制、对接工作等具有重要意义，也为监测系统的设计和研究提供重要参考依据[1]。空间目标的视星等参数主要取决于目标表面反射属性、目标有效反射面积以及太阳-目标-观测者三者位置关系[2-3]。目前，研究人员针对目标表面属性的差异，已建立朗伯模型和双向反射分布函数两种基本模型[4]。在目标有效反射面积的研究中，主要有简单几何体组合法[5-6]，以及较为改进的矢量分析方法[7]、区域网格化方法[8]以及网格化面元分割方法[9]等。组合法适用于标准几何体，计算精度较低；区域网格化方法侧重于研究表面属性不同的目标，对面元划分方法的研究不够深入；网格化面元分割方法对此作了改进，针对不同面型给出了建模公式，但在实际情况中达到收敛条件时面元分割数较大，不利于模型的快速计算。

为了优化计算速度和提高建模精确性，提出一种将卫星模型表面进行三角形面元分割的方法，利用三角形面元分割法快速求解面元参数，并建立收敛的有效反射面积和视星等计算模型。利用模型对在轨地球同步卫星FY-2进行有效反射面积和视星等仿真，并搭建了双水平式光电实验平台对目标卫星进行跟踪对比实验。

2三角形面元分割法

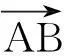
图1　三角形面元

由矢量分析原理分别求出三角形面元的单位法向量和面积：

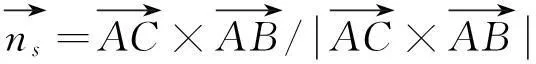
(1)

对目标卫星表面划分的三角形面元数量越多，表面模型越真实，也越接近卫星表面的实际情况，通过累加每个三角形面元的有效反射面积，即可准确计算卫星表面有效反射面积。以类圆柱体目标为例，利用三角形面元分割法分割圆柱表面，是将圆柱看成底面为正N边形的棱柱，通过对棱柱侧面和底面进行分割计算，得出每个面的有效反射面积，分割示意图见图2：

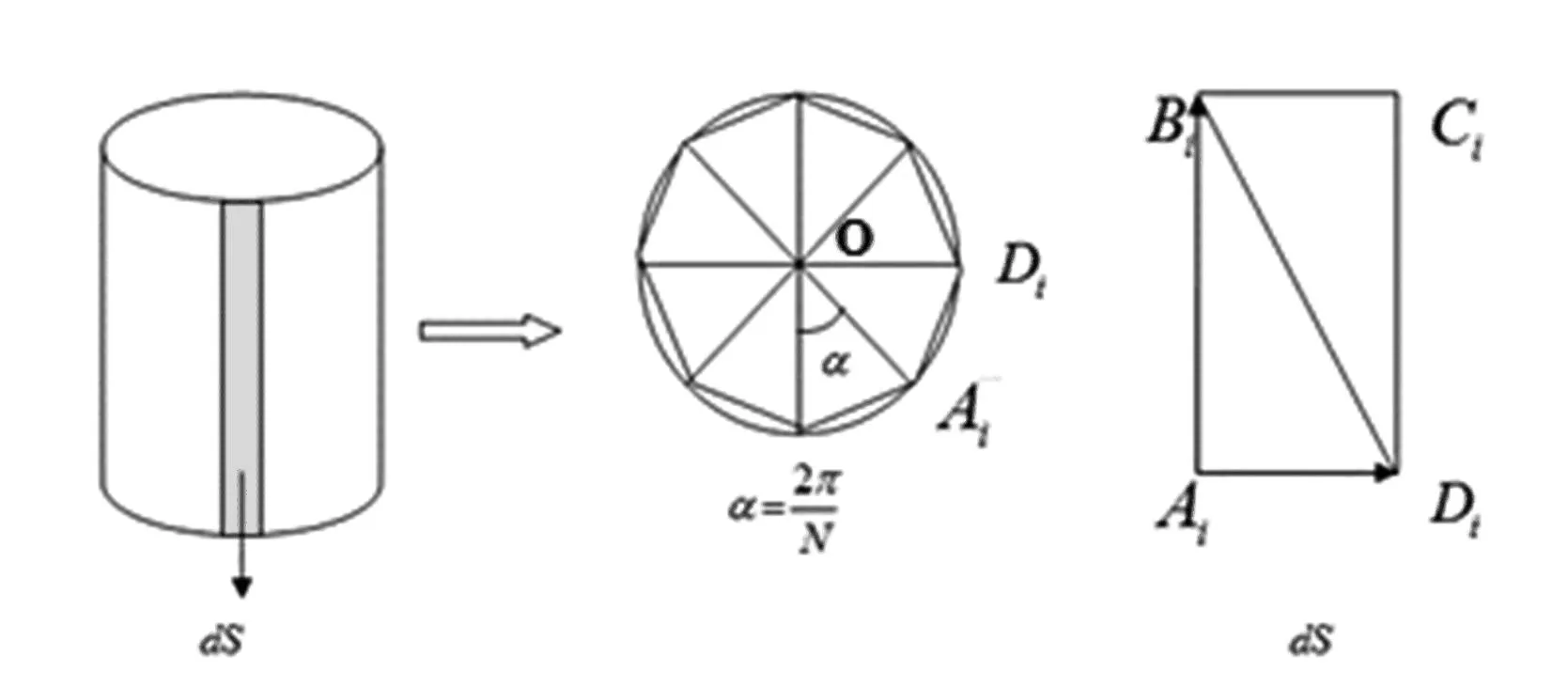
图2　三角面元分割法分割圆柱侧面和底面

假设圆柱面的底面半径为R，高度为H，则第i个面元各顶点坐标为：

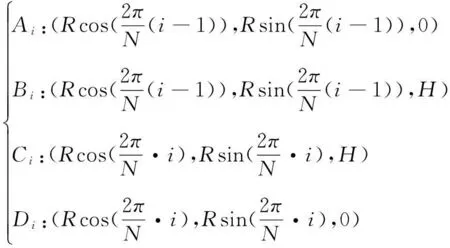
(2)

分割后的面元包括侧面面元和底面面元两部分，对于侧面面元，第i个矢量面元为：

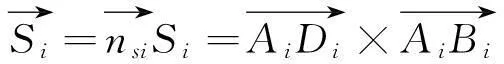
(3)

其中，单位方向矢量：

(4)

第i个面元的面积大小为：

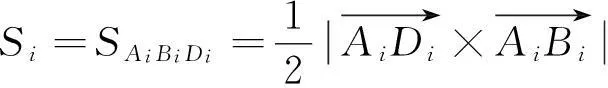
(5)

对于圆柱底面面元，第i个面元对应的上下两个面的法向量为：

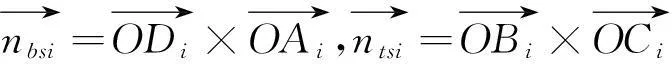
(6)

第i个面元对应的上下两个面的面积为：

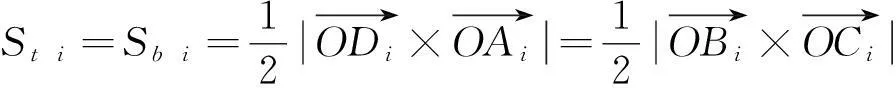
(7)

考虑空间目标表面的漫反射满足朗伯定律，入射太阳光与面元法线夹角，即太阳入射角为θ，观测方向光线与面元法线夹角，即光线反射角为β，如图3所示：

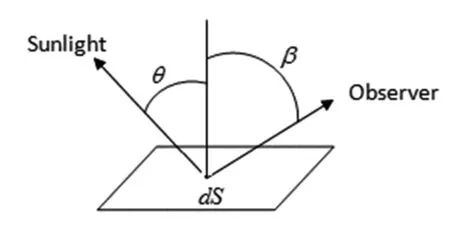
图3　太阳入射角与光线反射角

则第i个面元的有效反射面积为：

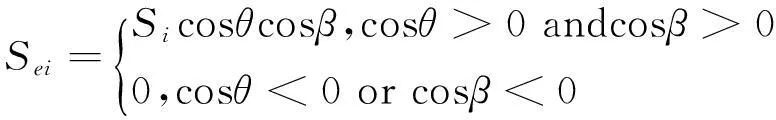
(8)

整个圆柱面的有效反射面积为：

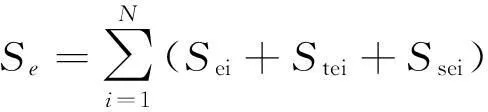
(9)

可以看出，由于目标运动姿态的改变，太阳-目标-观测点三者之间时空不断发生变化。任意时刻地面观测点只能观测到目标表面部分面元的反射光线，其他部分反射光线因为入射光线角度或者观测角度不满足条件而无法观测。对于地球同步轨道目标，在任意时刻，目标卫星与观测点保持相对静止，即β保持不变，而θ随着时间发生变化，因此在计算有效反射面积时，卫星表面满足θ与β同时处于0到π/2之间的部分为有效的计算区域[10]。下面从目标有效反射面积计算模型出发，推导在轨地球同步卫星的视星等计算模型，并对卫星的光学特性和计算模型的精度进行仿真。

3地球同步卫星视星等模型

3.1　计算模型

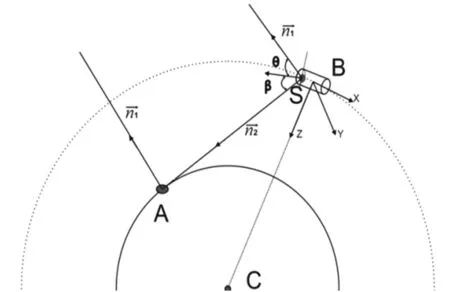
图4　空间目标坐标系

对目标视星等Mv，照度Em有如下计算公式[11]：

Mv=-26.74-2.5lg(Em/Es)

(10)

Em可由下式得到：

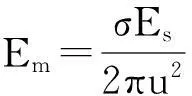
(11)

上述式中，σ为目标视星等表面漫反射系数，u为目标到观测站距离，Es为太阳在可见光波段范围内对应照度值。在公式(11)中，将面元积分∫cosθcosβdS的结果记为 Se，即目标有效反射面积，可得星等计算模型：

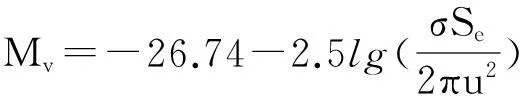
(12)

其中 Se即目标有效反射面积由公式(9)计算得到，下面根据Se与Mv模型公式对在轨地球同步卫星进行数据模拟。

3.2　数据模拟

模拟计算中，空间目标设置为我国自主研发的某地球同步轨道卫星FY-2，卫星国际编号29640，本体为柱体结构，柱体底面直径2.1 m，高1.6 m，姿态三轴稳定；表面反射系数0.2，轨道高度35779 km×35795 km，轨道倾角0.5135° ，偏心率0.0001163，每日绕地1.0028圈；选取观测站点为我国东部某地区，纬度30.2°，经度120.1°，观测站高度0，地方时T=UTCG+8，选取观测时间从1 May 2013 18:00 -1 May 2013 23:00 (UTCG)(白天天光背景较强，目标亮度较低)，时间间隔600 s。计算并仿真整个时间区间内太阳入射角、光线反射角、有效反射面积和目标视星等随时间变化如图5。

图5(a)表示太阳入射角与光线反射角随时间变化，图5(b)表示有效反射面积与视星等值随时间变化。可以看出，整个仿真时间段中太阳入射角在24.5°到94°之间持续增加，光线反射角在7.9°到8.1°之间微小变化(卫星偏心率不为零)，目标卫星相对地球保持静止。卫星在18:00有效反射面积较大，视星等值较低，目标较亮，但观测点日落时间为18:29分，此时天空背景辐射较强，不利于地面望远镜观测。考虑日落后昏影现象约半小时后消失，从19:00开始至22:00， 太阳入射角持续增加并低于90°，卫星一直处于观测点与太阳之间，光线入射方向与地面观测方向一致。此时，表面有效反射面积较大，视星等值有所增加但趋势较为平缓，目标亮度较高，利于观测。从22:00开始视星等值迅速增加，目标亮度减弱，22:50分以后太阳入射角超过90°，目标与太阳在观测点同一侧，目标进入地影中。在观测时间段19:00到22:00内，视星等计算值约为12.42~13.67。

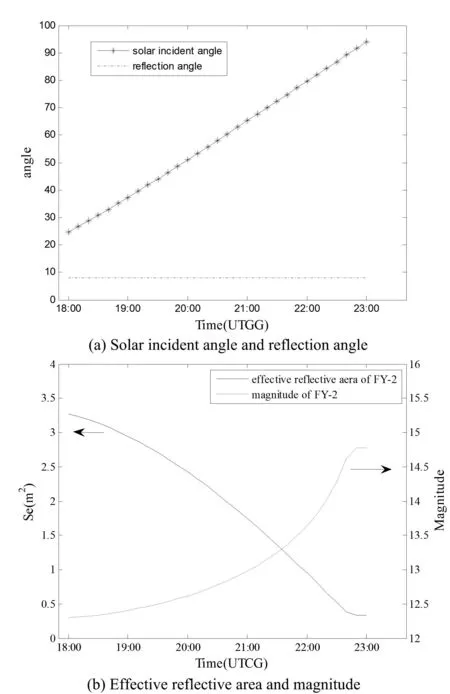
图5　太阳入射角、光线反射角、有效反射面积和目标视星等随时间变化曲线

3.3　算法精度

为了验证三角形面元分割法的计算精度，对目标卫星FY-2在20:00左右有效反射面积与利用文献[9]中的经验公式计算结果进行对比分析，图6为两种计算值差值比较。

在图6中，横坐标表示分割边数N，纵坐标ΔS表示利用公式(9)计算结果Se与利用经验公式计算结果Sf之差的对数值，即：

(13)

当分割边数0≤N≤50，两种计算方法差值波动较大，是因为在三角形面元分割中将表面曲面面元等效为平面面元而产生面型畸变；随着圆柱面分割数的增加，使用三角形面元分割法计算所得的有效反射面积越来越接近经验公式计算结果，当分割数N=256时，两种方法计算结果的差值已逼近10-3，相比于文献[9]中网格面元化方法对圆柱体表面分割数在N=1600时达到稳定收敛，本算法在结果逼近理论值的同时，表面面元分割数量较少，降低了计算复杂度。

4目标观测试验

4.1　光电探测平台

本次实验中采用搭载望远镜系统的双水平式跟踪平台，平台主要包括两部分：天文望远镜系统和二维转台，天文望远镜用来跟踪捕获目标，二维转台用来保证跟瞄系统精确性。其中，天文望远镜采用定制产品，套用马卡式200/2400型号规格，其光学系统采用高性能、优像质的三片马克苏托夫——卡塞格林系统，是由一块弯月折射镜及两块球面反射镜组成，确保光学系统品质可以达到衍射极限。望远镜的主要参数为：主镜长度80 cm，主镜口径为250 mm，焦距200 mm，集光力816 x，视场角为11 mrad，线视场为28 mm。实验中所用CCD靶面为1/2英寸，尺寸是7.5 μm×7.5 μm，并且可以实现最低 0.00002 lx@1.4F的超低照度。

4.2　实验结果分析

本次实验选于2013年5月1日在我国东部某地区(纬度30.2°，经度120.1°)展开，观测对象为上述地球同步轨道卫星FY-2，取晚上19点到23点每个整点时刻卫星在望远镜CCD靶面成像像点，并根据Hipparcos星表定位目标附近的恒星亮度，用对比法估计各时间段目标视星等值[11]，实验与理论计算值如下表1：

表1　实验结果与理论值对比

其中，M与E表示实验中得到的星等值与亮度, Mv与Em表示模型计算值(21:00以后望远镜观测效果较差，无法准确预测视星等)。从表1中可以看出，观测结果与计算值基本一致，观测星等值比计算值大0.1到0.2，实验观测的亮度比Em/E在1.18左右，这是由于星光透过大气时受到衰减和湍流效应而造成的一定误差，误差低于2%。

5结论

提出了一种计算地球同步轨道卫星有效反射面积的三角形面元分割法并建立卫星视星等计算模型。利用模型对在轨卫星FY-2的视星等进行快速仿真，仿真结果与实验符合较好。三角形面元分割法在确保模型精度的条件下，有效提高了计算效率。

创新性说明

提出一种三角形面元分割法计算卫星表面有效反射面积并建立视星等计算模型，利用模型对在轨卫星FY-2进行仿真，与网格化面元分割法对目标表面分割数为1600时达到收敛相比，采用三角形面元的分割数为256时，模型即达到收敛条件，计算得有效反射面积与经验公式计算差值接近10-3，在2013年5月1 日19:00-20:00时进行跟踪实验，目标视星等观测值为12.6~12.8。三角形面元分割法为提高建模精确性和优化计算速度提供了一种有效途径。

[参考文献]

[1]吴振森，窦玉红. 空间目标的可见光散射与红外辐射[J].光学学报，2003，23(10): 1250~1254.

[2]赵彬，杨苏辉，王世涛，等. 空间小目标的光学建模与模拟观测[J]. 光学学报，2009，29(12):3395-3403.

[3]王元明，杨福民，陈婉珍. 卫星激光反射器有效反射面积的计算与测试 [J]. 光电工程，2007，34(10)：25-29.

[4]刁华飞，李智. 基于天基光学探测信息的GEO目标识别研究[J]. 装备指挥技术学院学报，2010，21(05): 55-59.

[5]李斌成. 空间目标的光学特性分析[J]. 光电工程, 1989, 16(02): 21-26.

[6]谈斌，姚东升，向春生，等.类柱体空间目标的星等计算模型研究[J]. 光电工程，2008，35(7)：33-37.

[7]李晓燕，高晓东，朱耆祥. 矢量法在计算空间目标地面照度中的应用[J]. 光电工程，2003，30(4)：28-30.

[8]王付刚，张伟，等. 基于区域网格化的空间目标光学特性计算方法[J]. 航天返回与遥感，2012，33(2): 81-87

[9]鲍文卓，丛明煜，张伟，等. 基于面元网格化的空间目标光学特性计算方法[J]. 哈尔滨工业大学学报, 2010, 42(05): 710-715.

[10]余浩章，成求青. 目标光学有效反射面积计算模型研究 [J]. 飞行器测控学报，2005，24(3)：15-20.

[11]胡淼，徐国蕊，张慧，等. 地球同步轨道立方体目标的视星等测算[J]. 光电工程，2013，40(06):6-10.

责任编辑：刘海涛

The Calculation of Geosynchronous Orbit Satellite magnitude Based on Triangular Panel Method

Hu Miao，Deng Jing，Xu Guorui，Li Qiliang，Zhou Xuefang, Zeng Ran，Wei Yizhen，Lu Yang

Abstract:In order to describe the optical properties of geosynchronous orbit satellite, the star magnitude model and a triangular panel method to calculate the effective reflective area were built. The magnitude model was set up considering the temporal relationship between the sun, satellite and observation point with time. The simulation curves of FY-2 effective reflective area and magnitude vs. time were drawn based on the model and corresponding parameters. To astringe the magnitude model, the surface segment number of triangular panel method was 256, compared with the mesh-creation method was 1600. The complexity of the model was reduced by the triangular panel method. The difference in calculating the effective reflective area between triangular panel method and theoretical figure was up to 10-3. From 19:00 to 20:00 on May 1, 2013, FY-2 with 12.6 and 12.8 magnitudes was observed by using the Double Photoelectric Tracking System, the results were consistent with experimental data.

Key words:geosynchronous orbit satellite; magnitude; triangular panel method; effective reflective area; photoelectric tracking

收稿日期：2014-07-18

基金项目：浙江省自然科学基金项目(LQ13F010012)

作者简介：胡淼，杭州电子科技大学通信工程学院副教授，硕士生导师，博士，研究方向：激光技术及卫星跟瞄；邓晶，徐国蕊，李齐良，周雪芳，曾然，魏一振，卢旸，杭州电子科技大学通信工程学院(杭州 310018)。

中图分类号:P228

文献标识码：A

文章编号：1673-1794(2015)02-0034-04