基于组合权重TOPSIS模型的区域水资源承载力综合评价

项 琼

(新疆塔里木河流域希尼尔水库管理局，新疆 库尔勒 841000)

文章编号：1006—2610(2015)04—0006—05

基于组合权重TOPSIS模型的区域水资源承载力综合评价

项 琼

(新疆塔里木河流域希尼尔水库管理局，新疆 库尔勒 841000)

建立了包括水资源系统、社会系统、经济系统和生态环境系统4个方面20项指标的区域水资源承载力综合评价模型；引入熵权法和层次分析法计算各评价指标权重，提高了权重确定的科学性与客观性。以研究区内7个县市为研究对象，利用模型通过形成决策矩阵、确定权重、建立加权决策矩阵、计算各评价对象与理想解的相对贴进度，由此得到不同区域水资源承载力水平。结果表明：三江平原整体水资源承载力处于“中等”水平；7个县市中，七台河市与穆棱市水资源承载力为Ⅱ级，处于“较好”水平，鸡西市、鹤岗市、双鸭山市、佳木斯市与依兰县处于“中等”水平，以上结果符合三江平原的实际情况。随着区域社会经济的发展，应结合水资源承载力评价结果和区域特点，制定科学合理的水资源规划，以保证社会经济的发展与水资源的供给始终处于良性状态。

水资源承载力；逼近理想解法；综合评价；三江平原

0 前 言

水资源承载力是一个国家或地区可持续发展过程中各种自然资源承载力的重要组成之一[1]。作为水资源安全研究中的一个重要内容，水资源承载力评价是在对区域水资源特征、开发利用程度及工农业生产、生活和生态环境对水资源的需求等诸多方面分析的基础上，综合评价不同时期不同区域水资源开发利用对经济社会发展和生态环境保护的满足程度[2]。

区域水资源承载力的科学评价是制定本区域水资源规划与优化配置的基础。近年来水资源承载力综合评价已由定性评价发展到定量评价，由依靠主要指标构建简单评价体系发展到利用多指标构建综合评价体系；因子分析法[3-4]、层次分析法[5-7]、模糊综合评判法[8-10]及灰色关联度法等[11]方法先后被应用到区域水资源承载力水平综合评价中。以上方法虽有一定指导意义，但因子分析法对评价指标正态标准化过程中信息发生丢失、特征提取性下降，因子方差贡献率与指标实际应取权重值差别较大；层次分析法是在建立层次结构模型、构造判断矩阵基础上求特征值来确定各评价因子及指标重要性权重，判断矩阵主要受评判标准的支配，评判标准的客观性较难量化判断；模糊综合评判法对于比较复杂的水资源承载力评价系统，需要构造复杂的评价指标的隶属函数；灰色关联度法是以指标间相互关联比对结果为基础的客观性评价，但不能很好地反映人类行为与客观环境间相互作用。逼近理想解法(technique for order preference by similarity to ideal solution，TOPSIS)是近年来提出的求解多属性决策问题的一种新方法，又称为优劣解距离法。其原理是根据有限个评价对象与理想化目标接近程度进行排序，在现有的评价对象中进行相对优劣的评价[12]。崔振才等[13]应用TOPSIS评价了区域水资源承载能力；方崇等[14]提出了基于信息熵的灌区旱情TOPSIS综合评价方法，建立了干旱评价指标体系，对关中地区旱情进行评价；赵萌[15]等证明了相对熵的准确性和稳定性；王绍玉[16]等证实了相对熵在TOPSIS中的可操作性。

本文根据文献[17]数据资料，拟通过TOPSIS法构建区域水资源承载力综合评价模型，利用评价对象与正、负理想方案的相对熵求出与理想方案的贴近度，为研究区水资源承载力水平评价提供参考。

1 水资源承载力评价指标体系建立

1.1 评价指标及等级划分

根据文献[17]数据资料，研究区水资源承载力综合评价指标体系包括：水资源系统、社会系统、经济系统和生态环境系统4个层次的内容。其中水资源系统包括单位面积水资源量、水资源开发利用率、水资源可利用率与供水模数4项指标；社会系统包括人口密度、人口自然增长率、城镇化率、城镇人均生活用水量、农村人均生活用水量与人均水资源占有量；经济系统包括人均GDP产值、GDP增长率、第一产业占GDP比例、单位耗水生产GDP值、万元工业增加值用水量、耕地灌溉率、单位面积灌溉用水量及单位耗水粮食产量8项指标；生态环境系统包括森林覆盖率与生态环境用水率2项指标。

根据水资源承载能力和社会经济发展对水资源的压力角度将水资源承载力划分为5个等级，其中：Ⅰ级表示水资源承载力极高，水资源开发利用初具规模，开发利用潜力较大；Ⅲ级表示水资源承载力中等，水资源和社会经济处于平衡发展的状态；V级表示水资源承载力极低，水资源承载力已接近饱和，进一步开发利用的潜力较小。Ⅱ级和Ⅳ级属于过渡级别，其水资源承载力情况分别介于上述Ⅰ级与Ⅲ级、Ⅲ级与Ⅴ级之间。各指标具体含义及承载力等级划分标准值可参看文献[17]。

由此，选取影响研究区水资源承载力的4个方面20个指标进行综合评价。

1.2 指标权重

权重是评价系统状态因素的状态特征在评价系统结构中的重要程度，也是管理决策者对其重视程度。因此权重的确定非常重要，它的合理、正确与否关系到最终的评判结果的准确性。权重的确定方法主要有2类：一是主观赋权法，即指标权重由相关专家根据经验知识判断得到，这样虽然能比较充分地反映专家的知识和经验，给出评价指标实际意义上的重要性系数，但容易因个人的主观因素而造成偏差，如层次分析法(analytic hierarchy process，AHP)，能将复杂问题层次化，将定性问题定量化，但决策结果具有较强的主观随意性。二是客观赋权法，即根据原始数据之间的关系来确定权重，具有较强的数学理论依据，如熵权法，是依据评价指标所包含的信息量的大小确定指标权重，但熵权法不能给出评价指标实际意义上的重要性程度，只能反映评价指标为决策所提供的有效信息量的多少。因此，将主观权重和客观权重结合起来，形成综合权重更有利于真实反应评价指标权重。

1.2.1 墒权法

熵权法的基本思想是根据各数据序列本身对系统评价产生影响的变异来量化指标变化引起的综合效应，变异性大的指标一般带来对评价结果更大的影响。

将多目标决策矩阵X=(xij)m×n归一化，形成新的判断矩阵B=(bij)m×n。

(1)

式中：i为评价方案(对象)；j为评价指标；xmax、xmin分别为第j个指标在各个评价方案中最大、最小值；m为评价对象个数；n为评价指标个数。

定义第j个评价指标的熵值，则有：

(2)

(3)

则第j个评价指标的熵权βj，得客观权重向量β=(β1，β2，βj，…，βn)，即：

(4)

1.2.2 层次分析法

层次分析法AHP是由运筹学家萨迪(Saaty. T.L)于1977年建立的一种非结构决策理论，它可对复杂问题做出准确、科学决策，改变了长期以来人们对复杂系统主要靠主观判断、缺乏逻辑思维进行决策的状况，特别适用于难于完全进行定量分析的复杂问题。运用AHP法分析问题时，可分为建立层次结构模型、构造判断矩阵并赋值、层次单排序(计算权向量)与检验、层次总排序与检验等步骤，评价过程能很好地与人的思维过程相拟合，目前广泛应用于工程技术、经济管理等领域。

本文选择AHP法和熵权法2种方法对决策指标进行组合赋权，确定指标权重。

(5)

式中：αj和βj分别为利用AHP法和熵权法确定的第j个评价指标权重。

2 水资源承载力综合评价模型构建

TOPSIS法是根据有限个评价对象与理想化目标的接近程度进行排序的方法。其基本原理是通过检测评价对象与最优解、最劣解的距离来进行排序，若评价对象最靠近最优解同时又最远离最劣解，则为最好，否则为最差；正、负理想解分别是设想的最优解(方案)、最劣解(方案)。

2.1 形成决策矩阵

将评价指标分为K级，设多指标决策问题的方案集(方案集包括K-1个指标分级临界值)为M=(M1,M2,…,Mm,MJ1,MJ2,…,MJk-1)，指标集为C=(C1,C2,…,Cn)，Jk-1是方案集指标分级临界值序号，方案Mi对指标Cj的值为zij，形成多目标决策矩阵Z=(zij)m×n。

(6)

为消除评价指标具有不同量纲对方案决策带来的影响，需要对形成的决策矩阵进行无量纲化处理，构建标准化决策矩阵V=(vij)m×n。

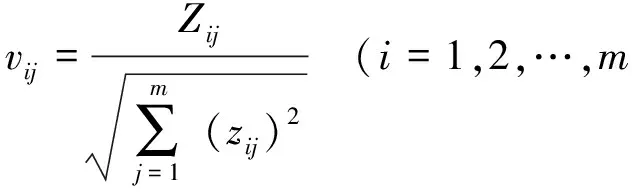
(7)

式中：vij为第i个方案的第j个指标的标准化值。将无量纲化矩阵与指标权重相乘，得加权标准化决策矩阵R=(rij)m×n；wj为每个指标组合权重，由式(5)确定。

rij=wj·vij(i=1,2,…,m；j=1,2,…,n)

(8)

2.2 计算理想解和负理想解

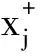
(9)

(10)

以公式(8)、(9)分别表示效益型指标(越大越优)和成本型指标(越小越优)的正负理想解。

2.3 各方案与理想解的相对贴近程度及方案决策

(11)

(12)

根据εi值的大小对方案Mi排序，εi越大则方案Mi越接近理想解，即方案越优，反之，方案越差。

3 模型应用

根据文献[17]中的相关数据资料，对研究区水资源承载力进行综合评价。

3.1 根据评价对象确定决策矩阵

将三江平原及7个县市的20个评价指标与4个分级临界标准共同构建决策矩阵Z，由式(7)进行无量纲化处理，得标准化决策矩阵V，详见表1。

3.2 确定指标权重

水资源承载力综合评价中各指标作用不同，影响程度有一定差异。通过AHP法[18]计算指标主观权重：

α=(0.0415，0.0576，0.0506，0.0718，0.0640，0.0645，0.0420，0.0144，0.0222，0.0424，0.0754，0.0420，0.0611，0.0458，0.0697，0.0600，0.0182，0.0576，0.0502，0.0488)；

由熵值法中式(1)～(4)计算出指标客观权重向量：

β=(0.0461，0.0542，0.0522，0.0604，0.0432，0.0512，0.0469，0.0470，0.0476，0.0478，0.0424，0.0414，0.0558，0.0620，0.0462，0.0600，0.0551，0.0450，0.0445，0.0511)；

由式(5)计算组合权：

w=(0.0381，0.0623，0.0527，0.0865，0.0552，0.0659，0.0393，0.0135，0.0211，0.0405，0.0637，0.0347，0.0680，0.0566，0.0642，0.0718，0.0200，0.0517，0.0445，0.0498)。

3.3 加权决策矩阵

根据式(8)处理得到加权决策矩阵X，详见表2。

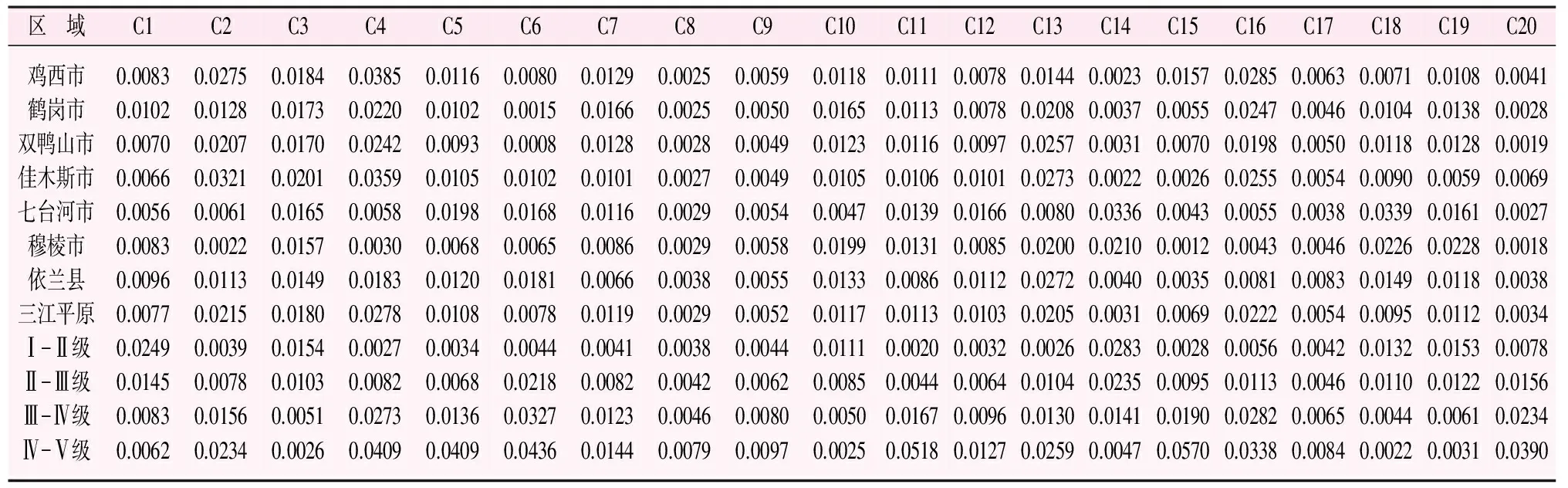
表2 三江平原水资源承载力评价指标加权决策矩阵表

3.4 理想解的相对贴进度计算

本研究涉及的各项评价指标有效益型指标(越大越优)和成本型指标(越小越优)，根据指标实际情况，分别选择式(9)或式(10)计算得到正、负理想解；由式(11)、(12)计算各评价方案与正、负理想解的相对熵值S+、S-及相对贴近度εi。

S+=(0.0249，0.0022，0.0201，0.0027，0.0034，0.0008，0.0041，0.0025，0.0044，0.0199，0.0020，0.0032，0.0026，0.0336，0.0012，0.0043，0.0038，0.0339，0.0228，0.0018)；

S-=(0.0056，0.0321，0.0026，0.0409，0.0409，0.0436，0.0166，0.0079，0.0097，0.0025，0.0518，0.0166，0.0273，0.0022，0.0570，0.0338，0.0084，0.0022，0.0031，0.0390)；

εi=(0.5181，0.7335，0.7154，0.5655，0.8313，0.9301，0.7139，0.6173，0.9653， 0.7940，0.3104，0.0063)。

根据各分区水资源承载力贴近度计算值及承载力等级临界值，计算得各分区水资源承载力等级(详见表3与表4)。

表3 水资源承载力等级临界值表

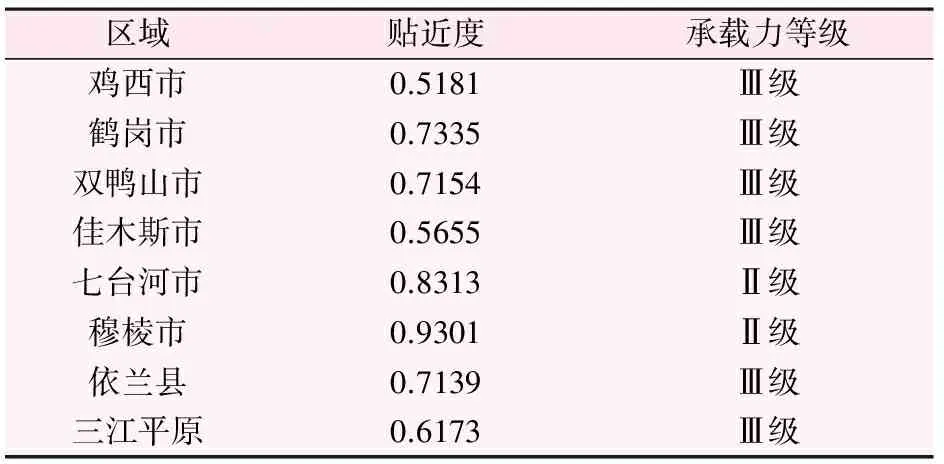
表4 三江平原分区水资源承载力评价表

计算结果表明，0.9653、0.794、0.310 4与0.006 3构成最终各方案相对贴近度分级标准。根据这一分级标准，三江平原整体水资源承载力处于Ⅲ级，区域内的双鸭山市、七台河市与穆棱市水资源承载力处于Ⅱ级，水资源承载力较强；鸡西市、鹤岗市、佳木斯市和依兰县水资源承载力处于Ⅲ级，水资源承载力中等，水资源和社会经济处于平衡发展的状态。

3.5 评价结果对比

为检验本文所建模型的准确性，通过与文献[17]结果对比，发现两者结论完全一致(见表5)，这验证了本模型的准确性。与此同时，文献[17]采用粒子群优化投影寻踪法对研究区进行水资源承载力计算，其计算结果客观性较强，而本文是基于组合权重(主、客观权重)对评价指标综合赋权，因此本文所建模型计算结果更加可靠与科学。

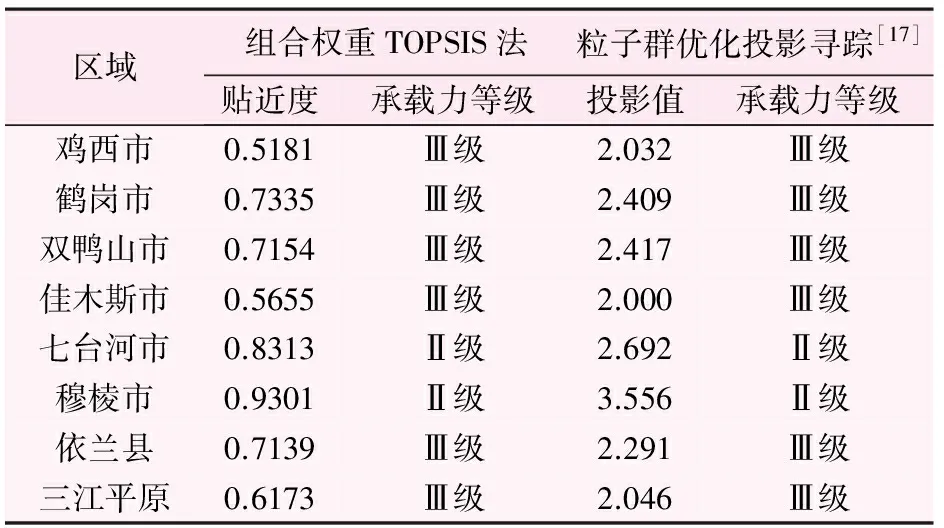
表5 模型评价结果对比表

4 结 语

(1) 本文构建了基于TOPSIS法的水资源承载力综合评价模型；对评价指标引入熵权法与AHP法计算组合赋权，评价模型计算方法简单，适用于多指标、多单元的大体系水资源承载力评价。

(2) 评价方法应用于三江平原水资源承载力综合评价，评价结果与实际情况基本一致。七台河市与穆棱市水资源承载力为Ⅱ级，水资源承载力有一定的富余；鸡西市，鹤岗市，双鸭山市，佳木斯市，依兰县与三江平原水资源承载力均为Ⅲ级，水资源和社会经济处于平衡发展的状态。

(3) 应用组合权重TOPSIS法所得水资源承载力计算结果与粒子群优化投影寻踪模型分析的结果完全一致，这不仅实现了方法对方法的检验，验证了结果的准确性，也从侧面说明了本文构建模型在区域水资源承载力评价中的可行性。

(4) 本文研究了黄水沟近60 a的径流变化特征，由于气候变化对径流量的影响存在着不确定性，因此还需要加强未来气候变化下的径流量预测及不确定性研究。

[1] 朱一中,夏军.关于水资源承载力理论与方法的研究[J].地理科学进展,2002,21(2):180-188.

[2] 曾浩,张中旺.湖北汉江流域水资源承载力研究[J].南水北调与水利科技,2013,(4):34-37.

[3] 吴琼.基于因子分析的青海省水资源承载力综合评价[J].水资源保护,2013,(1):22-26.

[4] 任玉忠,叶芳.基于主成分分析的潍坊市水资源承载力评价研究[J].中国农学通报,2012,(5):312-316.

[5] 王俊,李玉娟. 基于AHP的黑龙江省水资源承载力变动研究[J].黑龙江科技信息,2011,(34):56-57.

[6] 卜楠楠,唐德善,尹笋.基于AHP法的浙江省水资源承载力模糊综合评价[J].水电能源科学,2012,(3):42-44.

[7] 李青,陈红梅.基于FAHP的新疆喀什地区水资源承载力综合评价[J].资源开发与市场,2013,(8):851-854.

[8] 张曦,王武卫,齐养周,赵鹏霞,寇丽娟. 基于模糊识别理论的陕西省典型县域水资源承载力评价[J].干旱地区农业研究,2013,(6):232-237.

[9] 张国飞,刘廷玺,姜慧琴,包玉凤,王瑞东,芦小燕. 海拉尔河流域水资源承载力模糊综合评价[J].人民黄河,2011,(10):48-50.

[10] 孟丽红,陈亚宁,徐祥明,李卫红. 基于可变模糊评价法的塔里木河流域水资源承载力研究[J].水土保持通报,2012,(2):162-167.

[11] 魏光辉.基于熵权的灰色关联模型在水资源承载力评价中的应用[J].云南水力发电,2011,(2):4-7.

[12] 张先起,梁川.基于熵权的改进TOPSIS法在水质评价中的应用[J].哈尔滨工业大学学报,2007,39(10):1670-1672.

[13] 崔振才,曹广占. 应用逼近理想解法综合评价区域水资源承载能力[J].水文,2006,26(5):7-10.

[14] 方崇,苏超,黄伟军.基于信息熵大型灌区农业旱情的TOPSIS综合评价[J].中国农村水利水电,2011,(5):74-79.

[15] 赵萌,邱菀华,刘北上.基于相对熵的多属性决策排序方法[J].控制与决策,2010,25(7):1098-1100.

[16] 王绍玉,刘佳.城市洪水灾害易损性多属性动态评价[J].水科学进展,2012,23(3):334-340.

[17] 姜秋香,付强.三江平原水资源承载力评价及区域差异[J].农业工程学报,2011,27(9):184-190.

[18] 郭齐胜,董志明,单家元.系统仿真[M].北京:国防工业出版,2006:292-297.

The General Assessment on Bearing Capacity of Regional Water Resources Based on TOPPSIS Model of Combined Weight

XIANG Qiong

(Xinir Reservoir Administration of Xinjiang Tarim River Catchment, Kurle, Xinjiang 841000,China)

Models for the general assessment of the bearing capacity of the regional water resources in terms of water resources system, social system, economic system and ecological-environmental system with 20 indicators are built. The weight of each assessment indicator is calculated by application of the entropy method and the analytic hierarchy process (AHP) method. This improves the science and objectivity of the weight determination. Totally 7 cities and counties are taken as the study objects. Through the models and by establishment of decision-making matrix, weight determination, establishment of weight decision-making matrix, and calculation of the relative similarity degree between assessment objects and ideal solution, the bearing capacity of water resources in different region is derived accordingly. The study shows that the bearing capacity of the whole water resources of the Heilong River-Wusuli River- Songhua River plain is at the medium level. In the 7 cities and counties, the bearing capacity of the water resources of Qitaihe City and Muleng City is at Class II, belonging to the better level. That of Jixi City, Hegang City, Shuangyashan City, Jimusi City and Yilan Country is at the medium level. The study results are in compliance with the actual conditions of the Heilong River-Wusuli River-Songhua River plain. With development of the regional social economy, the scientific and reasonable plan of water resources shall be made out in combination of the assessment results of the bearing capacity of water resources and the regional characteristics to secure the social-economic development and the water-resources supply to stay all the time at good condition. Key words: bearing capacity of water resources; similarity to ideal solution; general assessment; Heilong River-Wusuli River- Songhua River plain

2014-12-28

项琼(1967- ),女，新疆库尔勒市人，工程师，主要从事水利工程建设管理工作.

新疆水文学及水资源重点学科资助(XJSWSZYZDXK20101202).

TV213

A

10.3969/j.issn.1006-2610.2015.04.002