基于改进支持向量机模型的开都河年径流量预测

王娟娟

(新疆金达鑫工程建设有限公司，新疆 库尔勒 841000)

文章编号：1006—2610(2015)04—0001—05

基于改进支持向量机模型的开都河年径流量预测

王娟娟

(新疆金达鑫工程建设有限公司，新疆 库尔勒 841000)

针对回归支持向量机(SVR)惩罚因子C和核函数参数g的选取对模型性能有着关键性影响以及在实际应用中存在参数选取等困难，提出基于启发式算法的PSO-SVR和GA-SVR年径流预测模型，以新疆开都河大山口水文站年径流预测为例进行实例研究。首先，利用DPS软件选取年径流影响因子，确定输入向量；其次，基于粒子群算法(PSO)、遗传算法(GA)基本原理，采用PSO、GA优化SVR惩罚因子C和核函数参数g，构建PSO-SVR和GA-SVR年径流预测模型，并构建基于网格划分(GS)与交叉验证(CV)算法相结合的GS-SVR模型作为对比模型。最后，利用所构建的模型对实例进行预测分析。结果表明：PSO-SVR和GA-SVR模型对开都河1996—2012年径流预测的平均相对误差绝对值分别为2.65%、3.22%，平均绝对误差分别为1.055亿m3和1.291亿m3，预测精度和泛化能力均优于GS-SVR模型，表明PSO和GA能有效对SVR惩罚因子C和核函数参数g进行优化，具有预测精度高、泛化能力强以及稳健性能好的特点。相对而言，PSO-SVR模型性能略优于GA-SVR模型。

粒子群算法；遗传算法；支持向量机；径流预测；开都河

0 前 言

提高径流预测精度对于水文预测预报具有重要意义，由于河川径流受多种因素的影响和制约，其预测常表现出复杂、随机、多维等特性，探寻能够有效提高径流预测精度的模型和方法是水文预测预报工作中的热点和难点。

目前，中长期径流预测常用模型有时间序列分析模型、回归分析模型、模糊分析模型、小波分析模型及灰色系统模型等。人工神经网络(Artifical Neural Network，ANN)具有较强的非线性映射能力、鲁棒性、容错性和自适应、自组织、自学习等许多特性，广泛应用于中长期径流预测预报中[1-3]。但由于ANN算法是基于渐近理论，仅在样本容量趋向于无穷大时其经验风险才趋近于实际风险，实际应用中面临泛化能力差、收敛速度慢及存在局部极值等问题[4,5]。回归支持向量机(Support Vector Regression，SVR)是20世纪90年代中后期发展起来的基于统计学习理论构建的典型神经网络，在径流预测预报中具有广泛应用[6-9]。SVR具有严谨的数学基础，通过统计学习中的VC维(Vapnik-Chervonenkis Dimension)理论和寻求结构风险最小化原理来提高泛化能力，已成为继ANN之后机器学习领域新的研究热点。然而，SVR用于回归预测时，惩罚因子C和核函数参数g的选取对模型的预测精度有着关键性影响。由于目前惩罚因子C和核函数参数g的选取尚无理论上的指导原则或方法，最优参数的选取多凭经验、实验对比等进行搜寻，极大地制约了SVR模型精度与泛化能力的提高[10]。目前，常采用基于交叉验证(Cross Validation,CV)意义下的网格划分(Grid Search,GS)方法来寻找最佳参数C和g。

粒子群算法(Particle Swarm Optimization,PSO)和遗传算法(Genetic Algorithm,GA)等启发式算法可以不必遍历网格内所有的参数点也能获得更大范围内的最佳参数C和g，使得全局最优。基于此，笔者基于PSO和GA算法原理，提出PSO-SVR、GA-SVR年径流预测模型，以新疆开都河大山口水文站1956—2012年径流预测为例进行实例验证，并构建GS-SVR模型作为对比模型,结果表明PSO-SVR和GA-SVR模型具有较好的预测精度和泛化能力。

1 预测模型

1.1 回归支持向量机(SVR)原理

SVR是基于VC维概念和结构风险最小化原则，通过同时控制模型的复杂度和逼近精度来获得较好的推广能力。在解决非线性回归问题时，SVR是将样本通过核函数将低维空间中非线性回归问题映射到高维空间，并在高维空间中求解最优回归函数。

SVR实现回归预测步骤归纳为5步。

Step1,设训练样本为(x1,y1),…,(x1,y1)∈Rm×R,则在高维特征中建立的线性回归函数为：

f(x)=wφ(x)+bw∈Rn,b∈R

(1)

式中：f(x)为回归函数预测值，即拟合值；w为空间超平面；φ(x)为非线性映射函数；b为偏置量。

Step2,定义ε线性不敏感损失函数为：

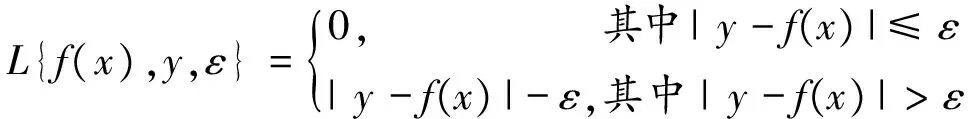
(2)

式中：f(x)为回归函数预测值；y为对应的真实值；ε为不灵敏参数，反映对误差的容忍度。

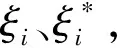
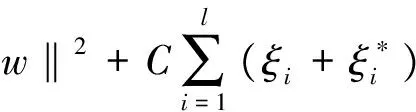
(3)

约束条件：

式中：C为惩罚因子，C越大表示对训练误差大于ε的样本惩罚越大；ε规定了回归函数的误差要求，ε越小表示回归函数的误差越小。

求解式(3)时，同时引入Lagrange函数，并转换成对偶形式：

约束条件：

(4)

式中：K(xi,xj)=φ(xi)φ(yi)为核函数。

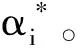
(5)

Step5，引入函数K(xi,x)，将w代入式(1)，得到f(x)表达式如下：

(6)

常用的核函数主要有线性核函数、多项式核函数、径向基核函数与两层感知核函数等。核函数的合理选取有助于提高模型精度，故本文选择径向基核函数作为SVR核函数。

Vapnik[11]等人研究表明，SVR的性能主要受惩罚因子C、核函数参数g和不敏感系数ε的影响。惩罚因子C决定着由训练样本产生的经验风险对模型性能的影响，即经验风险随着C值的增加而增加、减小而减小，当C值无穷大时，SVR结构风险趋于经验风险；而当C值趋于零时，则会导致模型失去解决问题的能力。核函数参数g的改变意味着改变映射函数，因此它主要影响样本数据在高维特征空间中分布的复杂程度。不敏感系数ε用于控制支持向量的个数，平衡模型的复杂程度与模型对训练样本维数的依赖程度，若ε值过小，则会导致模型“过拟合”，并且增加训练时间；反之，则会导致模型“欠拟合”。

因此，本文在给定不敏感系数ε的条件下，提出PSO、GA算法对SVR惩罚因子C和核函数参数g进行寻优，以期获得更好的预测效果。

1.2 PSO-SVR预测模型

(1) 粒子群优化算法

粒子群算法(ParticleSwarmOptimization,PSO)是近年来发展起来的一种新型启发式进化算法，最早由Kennedy和Eberhart[12]于1995年受鸟群觅食过程中迁徙和群聚行为而提出的群体智能全局随机搜索算法，具有简单、容易实现、收敛速度快和全局寻优等特点，并被证明在大多数情况下比遗传算法(GA)更有效。

(2) 基于PSO优化的SVR预测模型

定义目标函数：

(7)

本文选取式(7)作为PSO算法的目标函数，利用PSO算法对SVR参数(C,g)进行优化。具体算法步骤分6步。

Step1：选取SVR模型的训练样本和检验样本，设定惩罚因子C和核函数参数g搜寻范围。

Step2：确定目标函数，初始化PSO算法中的种群W=(W1,W2,…,Wn)、最大迭代次数、惯性权重ω、加速因子c1和c2为等参数取值，随机初始化待优化参数C和g的可行解位置W=(wi1,wi2,…,wis)T和速度V=(Vi1,Vi2,…,Vis)T。

Step3：根据初始化参数C和g，由式(7)计算适应值。若满足PSO收敛停止准则(达到训练误差或迭代次数)，则转至步骤Step6，否则转至步骤Step4。

Step4：更新粒子的位置、速度，计算PSO适应度值，记忆个体与群体所对应的最佳适应度位置Pi=(Pi1,Pi2,…,Pis)T与Pg=(Pg1,Pg2,…,Pgs)T，若Pi和Pg优于历史最优位置，则更新Pi和Pg。

Step5：重复Step4直到满足PSO收敛停止准则。

Step6：确定最佳惩罚因子C和核函数参数g，利用SVR模型对检验样本进行预测。

1.3 GA-SVR模型

(1) 遗传优化算法

遗传算法(GeneticAlgorithm,GA)的基本思想是将问题的求解表示成“染色体”，并置于问题的“环境”中，根据适者生存原则，从中选择出适应环境的“染色体”进行复制，即再生(reproduction)，并通过交叉(crossover)、变异(mutation)2种基因操作产生出新一代更适合环境的“染色体”群，这样不断重复，最后收敛到一个最适合环境的个体上，从而求得问题的最优解或次优解。GA具有隐含的并行性和强大的全局搜索能力，可以在短时间内搜索到全局最优点。因此，可利用GA对SVR惩罚因子C和核函数参数g进行优化。

(2) 基于GA优化的SVR预测模型

同样选取式(7)作为GA算法的目标函数，利用GA算法对参数(C,g)进行优化。具体算法步骤分6步。

Step1：选取SVR模型的训练样本和检验样本，设定惩罚因子C和核函数参数g的搜寻范围，对SVR惩罚因子C和核函数参数g进行染色体基因编码，产生SVR参数初始种群。

Step2：确定式(7)为目标优化适应度函数。

Step3：设定变异、交叉概率系数以及种群规模、进化代数等。

Step4：进行SVR训练，按式(7)计算GA适应度函数值，若满足GA训练停止准则(达到训练误差或迭代次数)，则转至步骤Step6，否则转至步骤Step5。

Step5：根据计算GA适应度值，对种群进行遗传、变异以及交叉操作，产生下一代SVR参数种群，利用得到的子代参数种群对SVR模型进行训练，计算适应度，若满足GA训练停止准则，则转至步骤Step6，否则返回步骤Step4。

Step6：结束训练，得到最佳惩罚因子C和核函数参数g，利用SVR模型对检验样本进行预测。

2 模型应用

2.1 数据来源与分析

新疆开都河大山口水文站1956—2012年57a的实测资料为例进行实例研究。利用DPS软件分析年径流量与1—12月月均径流量的相关性，分析结果如表1所示。

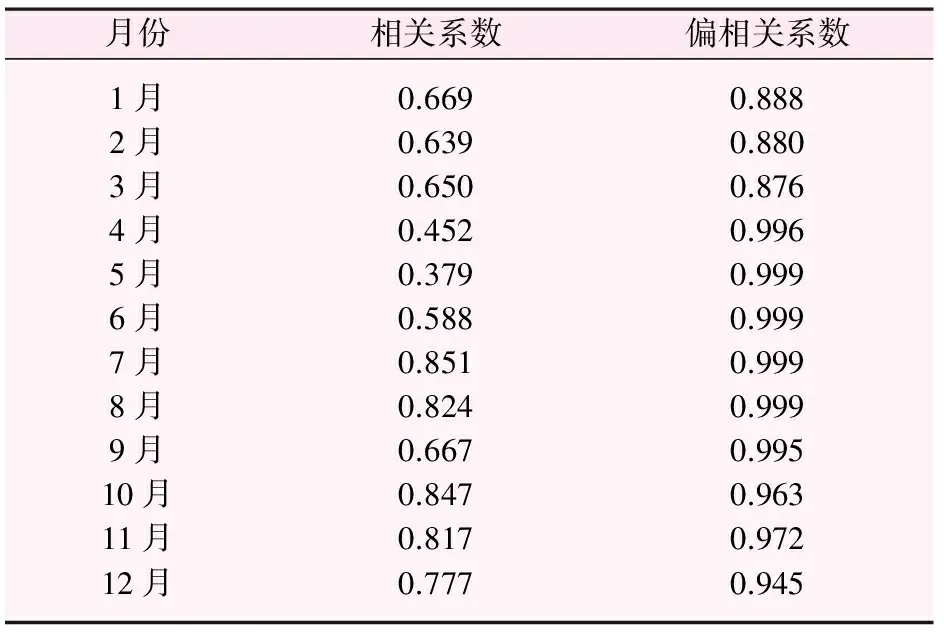
表1 开都河年径流量与各月流量的相关系数表

从表1可以看出，无论是简单相关系数还是偏相关系数，年径流与1—12月的月均径流量均呈正相关关系，相关系数在0.379～0.999之间，相关性十分显著。

2.2 模型计算

将PSO-SVR、GA-SVR和GS-SVR模型应用于开都河大山口水文站年径流预测的步骤分为训练及预测样本选取、数据归一化、模型构建、模型训练、预测结果分析5个步骤。

(1) 训练及预测样本选取。基于表1，选取与年径流在0.01水平(双侧)上显著相关的1—12月的月均径流量作为年径流量预测的影响因子，并以1956—1995年40a的实测资料作为训练样本，1996—2012年17a的资料作为预测样本。

(2) 数据归一化处理。利用式(8)对各径流序列进行归一化处理：

(8)

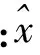
(3) 模型构建。本文基于Matlab软件环境和libsvm工具箱构建各SVR模型，选取1—12月的月均径流量作为模型输入向量，年径流作为输出向量，创建12输入1输出的PSO-SVR、GA-SVR和GS-SVR年径流预测模型。

(4) 模型的训练。利用选取的训练样本对PSO-SVR、GA-SVR和GS-SVR年径流预测模型进行训练，并选取平均相对误差绝对值VMRE为各模型性能的评价指标，公式如下：

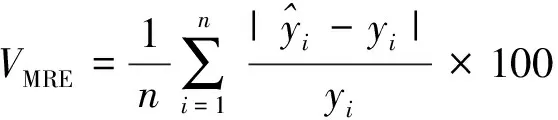
(9)

经反复调试，在下述参数设置条件下，PSO-SVR、GA-SVR和GS-SVR预测模型具有较好的预测效果。

1)PSO-SVR模型。选择径向基核函数作为SVR的核函数。惩罚因子C和核函数参数g的搜索空间分别设为0.1～100、0.01～1 000；局部和全局搜索学习因子c1、c2分别设为1.5、1.7；最大迭代次数设为200；种群规模设为30；惯性权重系数设为0.6；CV参数K值设为3；不敏感系数ε设为0.001(其他参数采用默认值)。利用PSO优化SVR模型中的惩罚因子C和核函数参数g，优化结果为：C=41.051 5；g=0.01。

2)GA-SVR模型。基于谢菲尔德(Sheffield)遗传算法工具箱，选择径向基核函数作为SVR的核函数。惩罚因子C和核函数参数g的搜索空间分别设为0～100、0～1 000；最大迭代次数设为200；种群规模设为50；变异系数设为0.9；CV参数K值设为5；不敏感系数ε设为0.001(其他参数采用默认值)。利用GA优化SVR模型中的惩罚因子C和核函数参数g，优化结果为：C=17.128 1；g=0.009 54。

3)GS-SVR模型。选择径向基核函数作为SVR的核函数。惩罚因子C和核函数参数g的搜索空间均设为2-2～26；步进大小均取0.1；CV参数K值设为5；不敏感系数ε设为0.001(其他参数采用默认值)，利用交叉验证法(CrossValidation,CV)确定SVR模型中的惩罚因子C和核函数参数g，寻优结果为：C=1.071 8；g=0.217 64。

PSO-SVR、GA-SVR与GS-SVR模型训练结果见表2和图1。

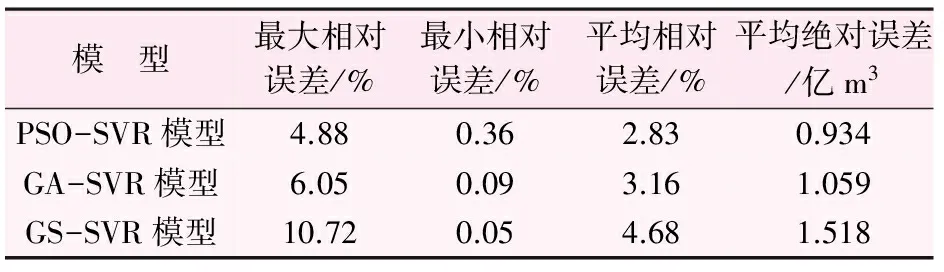
表2 不同模型训练结果误差分析表

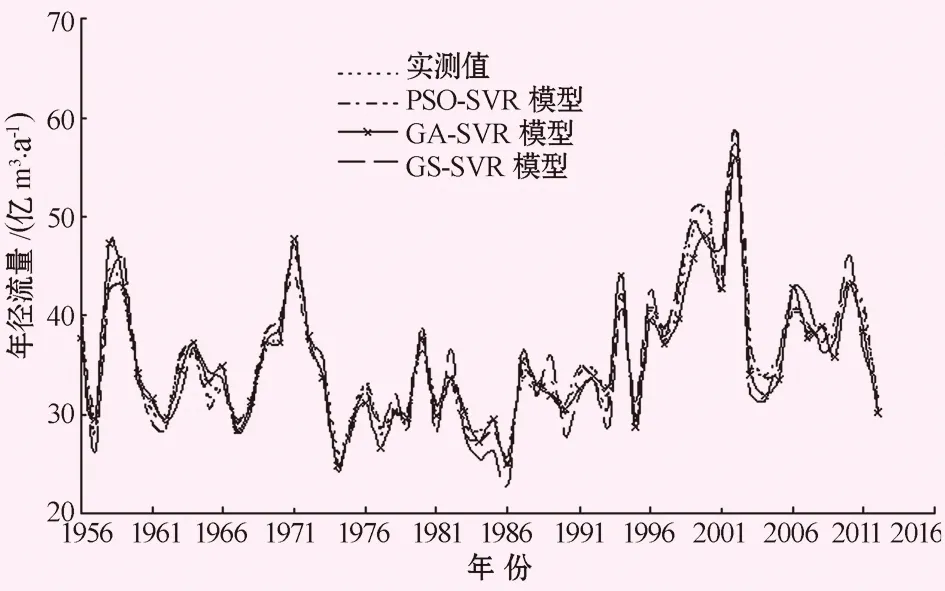
图1 不同模型训练结果与实测值对比图

由表2可知，PSO-SVR模型训练精度最优，平均相对误差为2.83%。平均绝对误差为0.934亿m3；GA-SVR模型训练精度次之，其平均相对误差为3.16%。平均绝对误差为1.059亿m3；GS-SVR模型训练精度最低，其平均相对误差为4.68%。平均绝对误差为1.518亿m3。

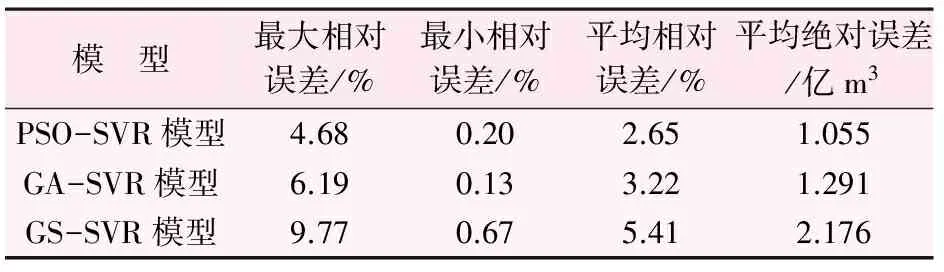
表3 不同模型预测结果误差分析表

(5) 预测结果分析。根据图1与表3可以得出以下结论：PSO-SVR和GA-SVR模型对开都河大山口水文站1996—2012年17a径流预测的VMRE分别为2.65%、3.22%，平均绝对误差分别为1.055亿m3和1.291亿m3，预测精度和泛化能力均优于GS-SVR模型，表明PSO和GA能有效对SVR惩罚因子C和核函数参数g进行优化；其次，从PSO-SVR和GA-SVR模型预测值来看，PSO-SVR和GA-SVR模型预测的相对误差分别在0.20%～4.68%、0.13%～6.19%之间，表明PSO-SVR和GA-SVR模型算法具有较好的预测效果和稳健性能。相对而言，PSO-SVR模型性能略优于GA-SVR模型。

3 结 语

在给定不敏感系数ε和径向基核函数条件下，提出SVR模型惩罚因子C和核函数参数g的PSO、GA优化方法，以新疆开都河大山口水文站年径流预测为例进行分析，并与具有良好回归性能的GS-SVR模型进行比较，结果验证了PSO和GA能有效对SVR惩罚因子C和核函数参数g进行优化。PSO-SVR和GA-SVR模型兼顾了启发式优化算法与结构风险最小化算法二者的优点，具有预测精度高、泛化能力强以及稳健性能好等优点，模型及方法可为相关预测研究提供参考。

[1] 崔东文. 多隐层BP神经网络模型在径流预测中的应用[J].水文,2013,33(1)：68-73.

[2] 崔东文. 改进Elman神经网络在径流预测中的应用[J].水利水运工程学报,2013,38(2)：71-77.

[3] 邓霞,董晓华,薄会娟.基于BP网络的河道径流预报方法与应用[J].人民长江,2010,41(2)：56-59.

[4] 田雨波.混合神经网络技术[M].北京：科学出版社,2009.

[5] 王雷.支持向量机在汽轮机状态监测中的应用[M].北京：北京师范大学出版社,2012.

[6] 李彦彬,黄强,徐建新.河川径流中长期预测的支持向量机模型[J].水力发电学报,2008,27(5)：28-32.

[7] 李彦彬,黄强,徐建新. 基于混沌支持向量机的河川径流预测研究[J].水力发电学报,2008,27(6)：42-47.

[8] 卫太祥,马光文.基于惩罚加权支持向量机回归的径流预测模型[J].水力发电学报,2012,31(6)：35-38.

[9] 张俊,程春田.基于蚁群算法的支持向量机中长期水文预报模型[J].水力发电学报,2010,29(6)：34-40.

[10] 崔东文,郭荣.基于几种参数优化的支持向量机在径流预报中的比较分析[J].水资源研究,2013,34(2)：34-38.

[11] 崔东文.支持向量机在湖库营养状态识别中的应用研究[J].水资源保护,2013,29(4):26-30.

[12] 史峰,王辉,郁磊,等.MATLAB智能算法30个案例分析[M].北京:北京航空航天大学出版社,2011.

Predication of Annual Runoff in Kaidu River Based on Modified Support Vector Machine

WANG Juan-juan

(Xinjiang Jindaxin Engineering Construction Co., Ltd., Kurle, Xinjiang 841000,China)

The annual runoff predication models of PSO-SVR and GA-SVR based on the heuristic calculation method are proposed aiming at the key impacts on the model performance by selection of the penalty factorCand the nuclear function parametergof SVR as well as the difficulty of parameter selection in actual application. The predication of the annual runoff at Dashankou gauge station on the Kaidu River in Xinjiang is studied. First, the impact factors of the annual runoff are selected by application of DPS software to finalize the input vectors; second, the predication models of the annual runoff of PSO-SVR and GA-SVR are built as well as the GS-SVR model based on the combination of GS and CV is constructed in accordance with the basic principle of PSO and GA and by application of the penalty factorCand the nuclear function parametergof SVR optimized by PSO and GA. Finally, the built models are applied for predication of practice. The analysis presents that the absolute values of the average relative errors of the annual runoff of the Kaidu River in 1996—2012 predicated by both PSO-SVR and GA-SVR are 2.65% and 3.22% prospectively. Their average absolute errors are 105.5 million m3and 129.1 million m3respectively. Their predication precision and generalization ability both are superior to those of GS-SVR model. This proves that both PSO and GA can effectively optimize the SVR penalty factorCand the nuclear function parameterg. They feature high prediction precision, strong generalization ability and good stability. Relatively, performances of PSO-SRV model are superior to those of GA-SVR model.Key words: swarm intelligence; genetic algorithm method; support vector machine; runoff predication; Kaidu River

2015-03-03

王娟娟(1981- )，女，新疆乌鲁木齐市人，工程师，主要从事水利工程建设管理工作.

TV121.4

A

10.3969/j.issn.1006-2610.2015.04.001