一类广义变分不等式解的存在性及其算法

韩小琴，何中全

(西华师范大学数学与信息学院，四川 南充 637009)

一类广义变分不等式解的存在性及其算法

韩小琴，何中全

(西华师范大学数学与信息学院，四川 南充 637009)

摘要：利用变分不等式的古典算法，在Hilbert空间中讨论了一类广义变分不等式问题(GVIP)，证明了GVIP解的存在性,给出了一个新的迭代算法，得到了GVIP解的强收敛定理.

关键词：广义变分不等式；解的存在性；迭代算法；强收敛性

变分不等式是非线性分析理论的重要组成部分,在力学、微分方程、控制论、数理经济、对策论、优化、分线性规划等领域中都有非常广泛的应用,因此,讨论变分不等式解的存在性及逼近解的算法等问题非常重要.最近,Wu等在Banach空间中介绍了一种新的广义f-投影算子[1-2],用于解决MVI问题.文献[3]对自反Banach空间上的广义投影算子做了深入研究，Li等运用广义f-投影算子证明了逆变分不等式问题IMVI逼近解的收敛性[4].受上述工作的启发,本文对广义f-投影算子做了推广,介绍了广义φ-投影算子,证明了一类广义变分不等式问题GVIP解的存在性,并且给出了这类问题的一个新迭代算法,得到了GVPI解的强收敛定理.

1预备知识

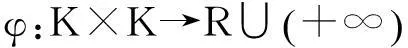
i) 关于第一变元下半连续,关于第二变元凸且连续；

iii) φ(x,y)=-φ(y,x),∀x,y∈K.

本文考虑广义变分不等式问题(GVIP):求x∈K,使得〈F(x),y-x〉+φ(x,y)≥0，∀y∈K.记GVIP的解集为S*.如没有特殊要求,本文将在以上条件下讨论GVIP.

下面介绍一些相关知识.

简称F是L-Lipschitz连续的.

2广义φ-投影算子

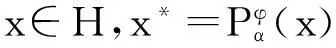
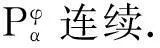
3解的存在性

定理1对∀α>0,x∈S*当且仅当Rα(x)=0.

当F为强单调映射时,GVIP有唯一解[1].

4广义φ-投影算法及其收敛性

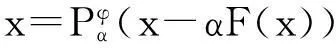
算法1对任意给定的x0∈H,计算e(xn,αn)和xn+1:

这里αn>0.为了获得算法1的收敛性,参照文献[4],给出下面定理.

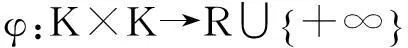
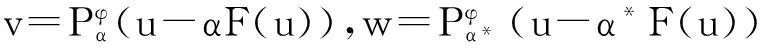
〈v-(u-αF(u)),w-v〉+αφ(v,w)≥0.

(1)

由式(1)得：

〈F(u)-e(u,α),αe(u,α)-α*e(u,α*)〉+φ(v,w)≥0，

(2)

〈F(u)-e(u,α*),α*e(u,α*)-αe(u,α)〉+φ(w,v)≥0.

(3)

式(2)+式(3)得

〈e(u,α*)-e(u,α),αe(u,α)-α*e(u,α*)〉≥0.

(4)

由式(4)得

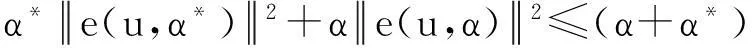
(5)

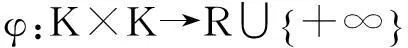
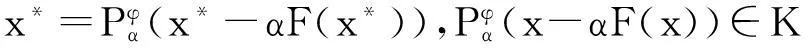
上述两式相加,得〈x*-x+αe(x,α),F(x)-F(x*)-e(x,α)〉≥0，即

〈x-x*-αe(x,α),F(x*)-F(x)+e(x,α)〉≥0.

(6)

因F强制,则

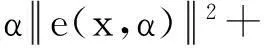
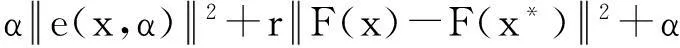
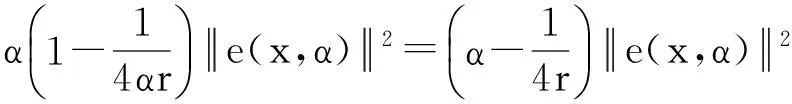
证毕.

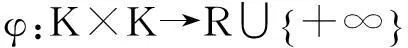
证明因xn+1=xn-e(xn,αn),x*∈S*,则xn+1-x*=xn-x*-e(xn,αn).由定理2和定理3知

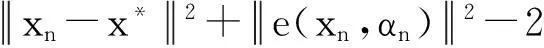
参考文献:

[1] Wu K Q, Huang N J. The generalizedf-projection operator with an application[J]. Bull Aust Math Soc, 2006,73(2):307-317.

[2] Wu K Q，Huang N J.Properties of the generalizedf-projection operator and its applications in Banach space[J].Comput Math Appl，2007,54(3):399-406.

[3] Li J L.The generalized projection operator on reflexive Banach spaces and its applications[J].Journal of Mathematical Analysis and Applications,2005,306(1):55-71.

[4] Li X,Li X S,Huang N J.A generalizedf-projection algorithm for inverse mixed variational inequalities[J]．Optimization Letters,2014,8(3):1063-1076.

[5] Wardrop J G.Some theoretical aspects of road traffic research[M]. London:Inst Civil Engineers Proc,1952:325-378.

[6] Solodov M V. Merit functions and error bounds for generalized variation inequalities[J].Journal of Mathematical Analysis and Applications,2003,287(2):405-414.

Existence and Algorithm of the Solutions for a Class of Generalized Variational Inequalities

HAN Xiaoqin, HE Zhongquan

(College of Mathematics and Information， China West Normal University，Nanchong 637009，China)

Abstract:Using the classical algorithm for generalized variational inequalities, a class of generalized variational inequalities (GVIP) is studied in the Hilbert space, the existence of solutions for GVIP is improved, a new iterative algorithm is given, simultaneously, and a strong convergence theorem of the solutions for GVIP is obtained.

Key words:generalized variational inequalities; existence of solution; iterative algorithm; strong convergence

通信作者：何中全(1955—)，男，教授，主要从事非线性分析研究.E-mail:lingjianshanshui@163.com

基金项目:教育部科学技术重点项目(211163).

收稿日期：2014-12-05

文章编号:1674-232X(2015)03-0319-04

中图分类号:O177.91MSC2010：49J40；47J20

文献标志码:A

doi:10.3969/j.issn.1674-232X.2015.03.016