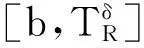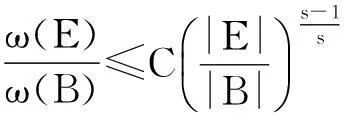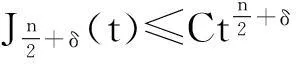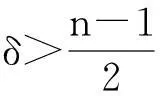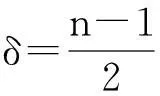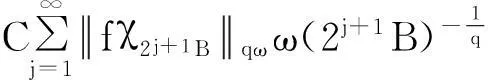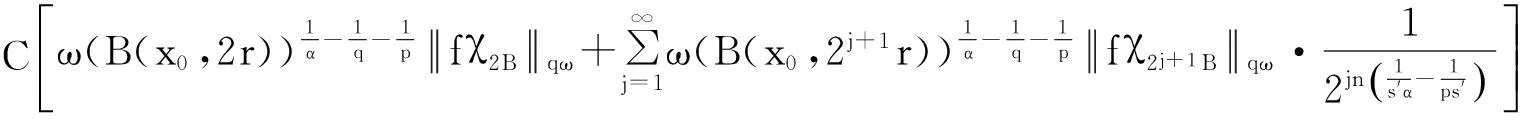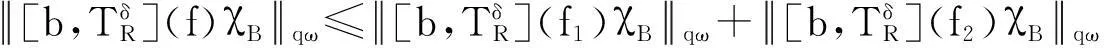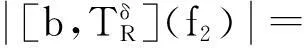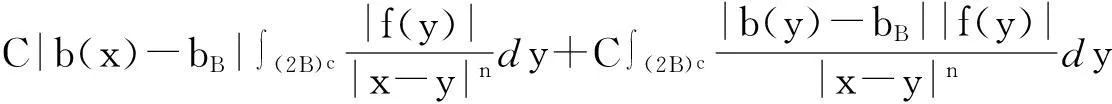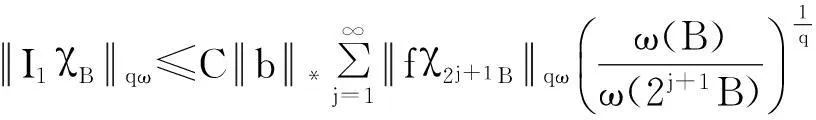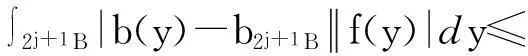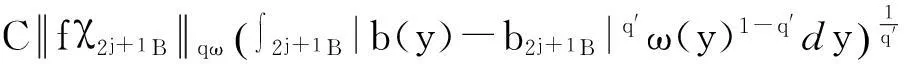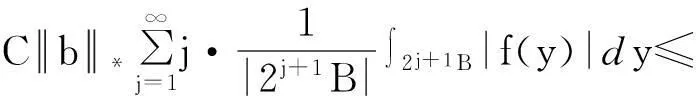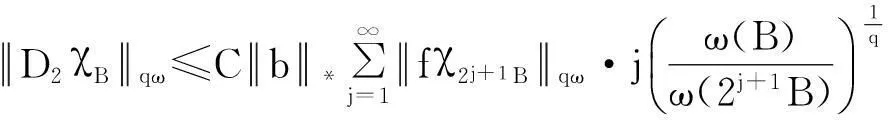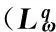Bochner-Riesz算子及其交换子在加权,Lp)α(Rn)空间上的有界性

吴　瑛，束立生，程美芳

(安徽师范大学数学计算机科学学院, 安徽 芜湖 241003)

吴瑛，束立生，程美芳

(安徽师范大学数学计算机科学学院, 安徽 芜湖 241003)

摘要：利用Aspan权性质及分析中的不等式，得到 Bochner-Riesz 算子及由BMO(Rn)函数b(x)和生成的交换子在加权共合空间(Rn)上的有界性,其中1

关键词：Bochner-Riesz算子；交换子；加权共合空间；Ap权

0引言

自1975年Holland[2]研究了共合空间(Lq,Lp)(Rn)的一些性质后,共合空间受到了广泛关注[3].1988年,Fofana[4]引入了空间(Lq,Lp)α(Rn).对于1≤q,p,α≤∞,定义,其中是一个伸缩变换.B(x0,r)表示以x0为中心,r为半径的球.χB(x0,r)表示其特征函数.|B(x0,r)|表示B(x0,r)的Lebesgue测度.共合空间(Lq,Lp)α(Rn)定义如下：(Lq,Lp)α(}.Fofana还证明了当且仅当q≤α≤p时,该空间是非平凡的.

文中出现的C表示与主要变量无关的正常数,并且在不同的地方可能取值不同.

1定义和引理

对于一个给定的权函数ω(x),记B的Lebesgue测度为|B|以及B的加权测度为ω(B),其中ω(B)=∫Bω(x)dx.

定义1[5]设10,使得对每个球B⊂Rn,有,则称ω(x)为一个Ap权,记作ω∈Ap.

定义2[6]设s>1,若存在一个常数C>0,使得对每个球B⊂Rn,有，则称ω(x)满足反向不等式,记作ω∈RHs.

文中主要结论的证明,还需要用到以下引理.

引理3[10-11]设b(x)∈BMO(Rn),则对任意的1≤p<∞,有.

在证明定理之前,先指出下面两个事实.

2定理的证明

由引理2知

(1)

则有

(2)

(3)

(4)

(5)

把式(5)代入式(4)，有

(6)

另一方面，

(7)

记P(y)=ω(y)1-q′,因为ω∈Aq则有P(y)∈Aq′.按照式(5)的推导过程有

(8)

(9)

则有

(10)

参考文献:

[1] Bochner S. Summation of multiple Fourier series by spherical means[J].Proc Natl Acad Sci U S A,1935,21(6):353-355.

[2] Holland F. Harmonic analysis on amalgams ofLpandLq[J]. London Math Soc,1975,10(3):295-305.

[3] Fourier J J F，Stewart J. Amalgams ofLpandLq[J]. Bull Amer Math Soc,1985,13:1-21.

[4] Fofana I. Étude d′une class d′espaces de fonctions contenant les espaces de lorentz[J]. Afrika Mat,1988，1(2):29-50.

[5] Muckenhoupt B. Weighted norm inequalities for the Hardy maximal function[J]. Trans Amer Math Soc,1972,165:207-226.

[6] Garcia-Cuerva J,Rubio de Francia J L. Weighted norm inequalities and related topics[M]. Amsterdam:North-Holland,1985.

[7] Wei X M,Tao S P.The boundedness of littlewood-paley operatoes with rough kernels on weighted(Lq,Lp)α(Rn) spaces[J]. Anal Theory Appl,2013,29(2):135-148.

[8] Gundy R F，Wheedem R L. Weighted integral inequalities for the nontangential maximal function，Lusin and Walsh-Paley series[J]. Studia Math,1974,49(2):107-124.

[9] Shi X L,Sun Q Y. Weighted norm inequalities for Bochner-Riesz operators and singular integral operators[J]. Pron Amer Math Soc,1992,116:665-673.

[10] Duoandikoetxea J. Fourier analysis[M]. Providence:American Mathematical Society,2000.

[11] John F,Nirenberg L. On functions of bounded mean oscillation[J]. Comm Pure Appl Math, 1961,14(3):415-426.

[12] Lu S Z,Wang K Y.Bochner-Riesz means[M]. Beijing:Publish House of Beijing Normal University，1988.

[13] Stein E M, Weiss G. Introduction to fourier analysis on euclidean spaces[M]. Priceton: Princeton University Press,1971.

[14] Alvarez J,Bagby R J,Kurtz D S,etal. Weighted estimates for commutators of linear operators[J]. Studia Math,1993,104(2):195-209.

WU Ying, SHU Lisheng, CHENG Meifang

(College of Mathematics and Computer Science,Anhui Normal University,Wuhu 241003,China)

Abstract:To use the nature of Aspanweight and inequality, this paper obtains the boundedness of Bochner-Riesz operators and the commutator formed by a BMO(Rn) function b(x) and ) on the weighted ,Lp)α(Rn) spaces, where 1

Key words:Bochner-Riesz operators; commutator; weighted amalgam space; Apweight

文章编号:1674-232X(2015)03-0308-05

中图分类号:O174.2MSC2010: 34K13

文献标志码:A

doi:10.3969/j.issn.1674-232X.2015.03.014