智能配电网网络重构算法综述

朱吉然，冷华，唐海国，张润贤，龚汉阳，李龙桂

(1.国网湖南省电力公司电力科学研究院，湖南长沙410007；2.湖南大学，湖南长沙410082)

智能配电网网络重构算法综述

朱吉然1，冷华1，唐海国1，张润贤2，龚汉阳1，李龙桂2

(1.国网湖南省电力公司电力科学研究院，湖南长沙410007；2.湖南大学，湖南长沙410082)

对配电网重构的常见算法和配电网络重构在国内外的研究现状进行了介绍，并对各类算法的优劣及应用场景进行了分析，强调算法的结合与细节优化对提高重构效果的作用。

智能；配电网；网络重构；数学优化；启发式；人工智能；算法

配电网是电力系统中连接发、输电系统和广大电力用户的关键环节，一般都采用闭环设计和开环运行的方式，结构呈辐射状。配电网络结构的调整以分段开关为主，还有少量的联络开关，可以通过改变网络中的分段开关与联络开关的开合状态，不断优化配电网络的结构，使得配电网运行方式更加合理，平衡线路负荷，降低网损，提高配电网供电的稳定性和可靠性，这种重新调整配电网运行方式的手段就称为配电网络重构。

早在20世纪70年代，Merlin与Back就研究发现，配电网络重构可以有效降低配电网的线路损耗。此后随着大量学者的深入研究，发现通过配电网络重构还可以有效均衡网络负荷、消除线路过载和提高供电电压质量。由于通过网络重构可以不需增加成本便能实现配电网络的优化运行，加之随着配电自动化技术的发展使得实时开关控制成为可能，因此网络重构的研究和应用具有很大意义和前景。在近几十年间，大量专家投入到了有关于配电网络重构的研究中，成功提出了一系列的重构算法及重构实施策略，本文就国内外主流的配电网网络重构算法进行介绍和分析，给出各算法的特点和优劣，为不同配电网络重构算法的进一步改进提供参考。

现有的配电网络重构仍以网络损耗的降低为主要目标，再追求电压稳定、供电可靠等，但是仍未实现非线性问题的优化，在优化过程中每次迭代都要求进行系统的潮流计算，花费大量的运行时间。为保证算法的运行速度并得到最优的结果，发展出了数学优化算法、启发式搜索算法和人工智能算法等。在2001年国内便有介绍各种主流算法的文献，研究进展与国外大致相同。配电网重构的算法仍在不断的改进，算法的优化过程也是重构计算量与准确性的均衡过程。现国内外主要的研究方向有多种重构算法有效组合研究、考虑实际配电网调度情况的重构算法研究以及充分结合配电网络自动化的重构研究等方面。

配电网络重构算法主要分为3大类:数学优化算法，启发式算法以及人工智能算法。

1 数学优化算法

数学优化算法是根据数学优化方法和原理从而得到最优网络的算法。整数规划法、分支定界法、非线性规划、动态规划等是数学优化算法中的常见算法。

1975年，Merlin，Back等人率先提出将数学优化算法与配电网最优重构相结合的方法来求取最优配电网结构，该方法使得结果独立于初始网络结构，可搜索出最优解及次优解〔1〕。

在此之后，配电网络重构的重要意义慢慢被人们所察觉，许多学者试着采用不同的数学优化算法来解决配电网重构问题。文献〔2〕提出利用组合负荷寻优的重构方法，利用最短路径理论搜索每个用电负荷的供电路径，选择最优的负荷排列顺序，从而获得全局最优解，适合求解网孔多，结构复杂的网络重构优化问题。

T.P.Wanger等人另辟蹊径，通过解决考虑二次费用的网络传输问题来处理以网损最小为目标的网络重构问题，利用分段线性函数表示二次功率损耗，并考虑了热容约束和馈线电压降落〔3〕。利用该方法，不需设置重构的起始条件与方案，能够通过优化最终得到辐射状的配电网络结构。

文献〔4〕忽略电压降落并将用电负荷用恒定电流来代替，将配电网重构问题看作非线性规划问题来求解。

数学优化算法起步较早，现已经拥有非常成熟的算法基础，用于配电网络重构，可以在不考虑配电网初始结构的情况下获得全局最优解。但是由于数学优化算法要求对所有解进行评估，持续的寻优过程会耗费较长的计算时间。并且应用于实际配电网中时，随着网络结构逐渐复杂，计算规模呈指数发展，因此，数学优化算法只适合于求解简单的配电网络重构问题，离实际的复杂配电网应用还有一定差距。

2 启发式算法

启发式算法是在分析目标函数和约束条件的基础上，通过直观或者经验构造规则，计算可行解。启发式算法可以避免很多无用的计算，构造规则具有很大的灵活性，可以简化复杂问题。但是规则的提出并不具备理论上的支持，随着配电网规模、配电网类型的变化需要重新寻找规则，得出的可行解与最优解的偏离程度不可预测。

2.1 最优流模式法

1989年，Darish Shirmohammadi等人提出了一种启发式算法，被称为最优流模式法〔5〕，该算法求解的基本思想为:首先闭合这个网络中所有的联络开关，然后只考虑支路的电阻求得系统的最优流模式 (在满足KVL和KCL条件下的网络电流分布)，最后断开网络中电流最小的支路，每断开一条支路可以解开一个环，然后重复网络的最优流计算及最小电流支路的断开，直到所有环都被解开，整个网络成为辐射状。

最优流模式法利用网络的最优流计算问题来替代重构中的开关操作组合问题，使得复杂的问题简单化。该算法的优势在于无需考虑网络的初始状态，容易获得全局最优解。但是，在该算法中每进行一次开关的断开都需要进行一次潮流计算，使得整个算法的计算量大；闭合网络中所有联络开关后，整个网络存在着多个环网，各个环网中的环流相互影响，开关断开的先后顺序会大大影响重构结果；在最优流模式下断开最小电流支路可以减少网损这一启发式规则缺乏理论依据。

S.K.Goswami等人为了消除网络中环流的影响，提出先确定断开支路、闭合联络开关的方法〔6〕。但是作者提出的每个环路中只能断开一个开关的方法只能适合于各环路间没有公用开关的简单电网。

文献〔7〕 在文献〔6〕 的基础上进行改进，提出一种新的算法。在算法中将环路支路和辐射支路分开考虑，将环路支路中的阻抗简化为电阻而辐射支路的阻抗仍保留为阻抗形式，估算网络损耗的变化程度来打开开关，在求最优流时能更加符合实际情况。

文献〔8〕对最优流算法做了一系列改进。首先提出新的启发式规则，以改变后使得网络损耗的增量值最小为标准，具备了理论上的基础；其次，讨论了如何避免重构时是否会产生孤立网络的判断问题，并给出了判断的方法:设从i，j两节点看进去的等值电阻为Req，支路ij的电阻为Rij，只有当Req不等于Rij时，才可以打开该支路，所以该方法只需一个判断语句就能实现；该算法用补偿法计算开关打开后的潮流，以减少计算量，并可判断其它支路有无过载。

2.2 支路交换算法

1988年，S.Civanlar等人首次提出了配电网络重构的支路交换算法〔9〕。该算法将网络负荷用恒定电流表示，首先利用潮流计算得到网络初始潮流与网损，然后一次闭合一个联络开关并决定一个需要打开的分段开关以保证网络重新恢复成辐射状，这样的一次联络开关闭合与分段开关断开称为一次开关交换。为了保证每次的开关交换操作都能够降低网络损耗，文献〔9〕中给出了计算开关交换操作前后网络损耗变化的公式:

式中 ΔP为开关交换操作前后的网损的变化量；D为负荷转移区域内节点的集合；i(j)为与联络开关相连相对电源节点电压降落较小 (较大)的节点；Ii为节点i的电流；Rloop为联络开关闭合后环网的电阻总和；Vi(Vj)为节点i(j)相对于电源节点的电压降。

根据上述公式建立一组启发式规则:由于公式中后面一项恒为正，为保证ΔP为负，网损下降，需要闭合节点电压差最大的联络开关，使得电压降落较小的节点承受负荷。

文献〔10〕提出改进的支路交换算法，以电压幅值差代替电压差的幅值，把记为Ix， 得到公式求出理想转移电流和负荷，对比节点负荷、电流值与理想值之间的距离来获取较优解，减小计算量。

文献〔11〕提出用近似网损替代精确网损，可以快速准确找到最佳操作开关，而且只需计算初始潮流，解决了传统支路交换法需要多次计算潮流的问题。

文献〔12〕提出和证明了二次电流矩定理，利用二次电流矩均衡度评价优化程度以决定断开或合并开关，该方法概念清晰，方法简捷，开关操作次数少。

支路交换法的优点在于只需估算支路交换过程中发生的网络损耗变化值，计算量小，无需重新计算潮流。利用启发式规则可以减少需要考虑的开关组合，能够快速确定更优的网络结构，但是最优解受初始状态影响，由于每次只能进行一次拓扑调整，无法保证获取全局最优解。

3 人工智能算法

随着人工智能算法在各个领域的普及，学者们也慢慢将人工智能算法用于解决配电网络重构问题。人工智能算法与传统的算法相比鲁棒性较好、可应用于大规模的配电网络，并且人工智能算法方便应用于多目标优化，使得算法更加适用于实际的配电网络重构。

3.1 基于人工神经网络的配电网络重构

人工神经网络算法将神经网络的学习过程应用到配电网重构的求解最优解的过程，建立实际问题的输入与输出之间的对应关系。将最优解与输入样本之间的潜在关系存储到神经元与神经元之间的联系中，并用于该类样本中，从而解决配电网重构问题。

人工神经网络的改进主要集中于对负荷进行分类，减少训练样本的负担，提高训练速度。文献〔13－14〕分别按区域和按用途分类，降低了配电网重构的复杂度，减少了计算时间。

由于人工神经网络以黑盒子的形式建立输入输出模型，不用考虑内部的关系，无需潮流计算和网损估计，利用人工神经网络可以很程度上减少计算重构计算的耗时，因此该算法可以算是目前速度最快的重构算法。但重构结果的质量取决于样本的数量和质量，神经网络算法的精度浮动性比较大，需要事先的准备较多 (训练样本，建立人工神经网络)，况且获取有一定规模的配电网数据很困难，不适合大规模应用。

3.2 基于模拟退火算法的配电网络重构

模拟退火算法模拟的是物理退火过程，在算法中以一定概率接受较差解 (以降低网损为基准)来避免局部最优解的问题，以网损变化程度、温度或迭代次数为结束判据。

1990年，Hsiao-Dong Chiang等人将模拟退火算法应用到了配电网重构的研究中〔15〕。在开始时简化潮流计算，当温度下降到一定程度时再用严格计算，提高精度，最后达到加快计算速度的目的。

文献〔16〕对模拟退火算法进行了改进。在算法中，将每一轮得到的最优解作为下一轮计算时的初始解，这样使得每一次得到的解都比前一次解更加接近最终结果，使得算法对参数的依赖性降低，也降低了算法的计算量。

模拟退火算法的优势在于不依赖初始结构，就能得到最优解，但是该方法需要考虑退火方案的的设计，并且受参数影响较大。计算量大，随机产生的重构方案大多没有意义，迭代次数、温度的设计对计算时间和解的准确性影响较大。对模拟退火算法进行改进时，一般主要针对接受较差解概率、温度变化函数等方面进行优化。

3.3 基于遗传算法的配电网络重构

遗传算法模拟的是生物遗传进化的过程，挑选优秀的上一代个体遗传至下一代并随机创造新的个体。以个体中每位基因的编码值表征开关的开合，通过计算系统的目标函数值来构造适应度函数。适应度函数值作为遗传算法确定搜索方向依据，其值越大表明目标函数优化的程度越好。当配电网络重构选择网络损耗最小为目标函数时，个体适应度值的计算可以采用如下表达式〔17〕:

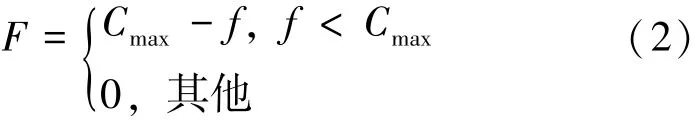
式中 f为目标函数即网络损耗；F为适应度函数；Cmax为一给定值。

遗传算法能一次产生大量的解，发现最优值的几率很高，能够实现快速全局收敛；然而，选取不同的初始基因串会得到不同的优化结果，产生解寻优需要大量时间，易受交叉率和变异率的影响。

文献〔18〕对遗传算法中的交叉操作算子进行了改进，提出部分匹配逆转交叉法，一个基因的某种变异来取代相同基因的交叉问题，也能使得即使种群发展到个体差异性小时仍能产生新的基因，从而扩展搜索空间，避免陷入局部最优解。

文献〔19〕通过治病操作清除劣质基因，文献〔20〕提出基于一种免疫机制的免疫遗传算法，通过构建疫苗库和设计免疫算子来抑制进化中的退化和波动，在确保解的质量同时，具有较快的收敛速度。

文献〔21〕提出了基于环路的改进遗传重构优化算法。该算法考虑了树状支路的开关应处于闭合状态，缩短了基因的长度。改进初始解的产生方法，使得初始解均为可行解；改进了适应度函数，改进交叉率和变异率，使算法具有一定的自适应性，尽可能的避免陷入局部最优解的状况，优化了遗传算法的效率和可靠性。

人工智能算法是仿照自然规律、自然结构(如模拟神经网络、模拟退火、模拟遗传)等原理设计算法，这种算法的优势在于内容丰富，应用范围广泛。但是智能算法往往是不断产生大量解，不断筛选，计算量较大，需要对算法各方面进行改进以满足实际应用需求。

4 其他配电网络重构算法

He S和 Wu Q H首先提出种群搜索优化(group search optimizer，GSO) 算法〔22－23〕，在文献〔24〕中，作者将其应用于配电网络重构，具体步骤为:①定义发现者为种群中网络损耗最小的个体，其他个体分为游荡者和加入者；②应用支路交换法处理发现者，游荡者用于随机搜索解，加入者则逐步靠近发现者，执行追随搜索；③结合局部寻优和全局搜索的优势，有效弥补了基于人工智能的算法以及启发式规则的缺点，能够加快搜索速度，从而具有较好的全局收敛性。

文献〔25〕在配电网重构中引入禁忌搜索算法，通过优解存储和禁忌准则避免算法陷入局部最优，将满足藐视规则的配适值最优解解禁，替代当前解，不断循环，保证算法最终能够获得全局最优解。

文献〔26〕提出的免疫算法模拟的是生物免疫过程，利用目标函数和约束条件模拟入侵生物体的抗原，利用可行解模拟免疫系统的抗体，利用可行解与最优解的逼近程度模拟抗体和抗原的亲和度，不断选出亲和度较高的抗体进行变异克隆，最终得到最优解。

文献〔27〕提出和声算法，将重构的解比作声调的和声，各重构环中断开的支路比作乐器的音调，评估目前和声的状态。首先用和声记忆库存储初始粒子，以较大的概率在库中选解，并用较小概率进行扰动，产生的新解若优于库中的最差解则进行替代，不断迭代至满足最终条件。

文献〔28〕则使库中侯选解和扰动的概率随粒子信息的变化而变化，并提出了基本环及基本环矩阵的相关概念，提出了基本环矩阵的自动生成算法以及避免不可行解的编码方法。

文献〔29〕则利用模拟退火算法的优势避开局部最优解，采用支路交换算法控制降温次数以及控制温度下开关开合次数，通过实际可以验证配电网络重构的计算速度大大提高，并能避免局部最优解。

文献〔30〕使用遗传算法计算初始结构和温度，运用模拟退火算法搜索全局最优解，使用快速潮流计算方法来加快速度，在降损效果、迭代次数、迭代时间上都有所改善。

文献〔31〕利用粒子群算法的群体并行搜索能力与模拟退火算法解的多样性相结合，从而既克服了粒子群算法的早熟现象，又加快了退火操作的速度，降低参数的影响。

除此之外，现有的配电网络重构算法还包括结合实际运行经验确定最优解的专家系统法；利用寻找最小生成树的方法来确定配电网最优结构的最小生成树算法〔32〕；采用粒子群整体运动进行配电网络重构求解的粒子群算法〔33〕，等等。

目前为止，用于配电网重构的方法已有很多，算法都已比较成熟，但是为了能够实现实时网络重构，算法的快速性和准确性还需要进一步的提升。实际上要得到一个能够应用于实际重构的算法需要对各算法进行互相借鉴和对算法的细节进行改进，取长补短才能不断提高算法的性能。

〔1〕Merlin A，Bask.H.Search for a minimal-loss operating spanning tree configuration in urban power distribution system〔C〕.Proc of 5thPower Systems Comp Con，Cambridge，UK，1975:2-6.

〔2〕余贻鑫，段刚.基于最短路算法和遗传算法的配电网络重构〔J〕.中国电机工程学报，2000，20(9):44-49.

〔3〕Wanger TP，Chikani AY，Hackam R.Feeder Reconfiguration for Loss Reduction:An Application of Distribution of Distribution Automation〔J〕.IEEE Trans on Power Delivery，1991，6(4): 1 922-1 931.

〔4〕 AokiK，Ichimor TI，Kanezashi M.Normal State Optimal Load Allocation in Distribution Systems〔J〕.IEEE Trans on Power Delivery，1987，2(1):147-155.

〔5〕 Shirmohammadi D，Wayne Hong H.Reconfiguration of Electric Distribution Networks for Resistive Line Losses Reduction〔J〕. IEEE Trans on Power Delivery，1989，4(2):1 492-1 498.

〔6〕Goswami SK，Basu SK.A New Algorithm for the Reconfiguration of Distribution Feeders for Loss Minimization〔J〕.IEEE Trans on Power Delivery，1992，7(3):1 484-1 491.

〔7〕邓佑满，张伯明，相年德.配电网络重构的改进最优流模式算法〔J〕.电网技术，1995，19(7):47-50.

〔8〕吴本悦，赵登福，刘云，等.一种新的配电网络重构最优流模式算法〔J〕.西安交通大学学报，1999，33(4):21-24.

〔9〕 Civanlar S， Grainger J J， Yin H， et al.Distribution Feeder Reconfiguration for Loss Reduction〔J〕.IEEE Trans on Power Delivery，1988，3(3):1 217-1 223.

〔10〕毕鹏翔，刘健，张文元，等.配电网络重构的改进支路交换法〔J〕.中国电机工程学报，2001，21(8):98-103.

〔11〕汪韩，黄彦全，张永超.改进的支路交换算法在配电网重构中的应用〔J〕.电气开关，2007(4):45-47.

〔12〕屠强，郭志忠.辐射型配电网重构的二次电流矩法〔J〕.中国电机工程学报，2006，26(16):57-61.

〔13〕 Kim H，Jung K H.Artificial Neural-Network Based Feeder Reconfiguration for Loss Reduction in Distribution Systems〔J〕. IEEE Trans on Power Delivery，1993，8(3):1 356-1 366.

〔14〕Kashem M A，Jasmon G B，Mohamed A，et al.Artificial Neural Network Approach to Network Reconfiguration for Loss Minimization in Distribution Networks〔J〕.ElectricPower＆Energy System，1998，20(4):247-258.

〔15〕Chiang Hsiao-Dong， Rene Jean-Jumeau. Optimal Network Reconfigurations in Distribution Systems: Part 2 Solution Algorithms and Numerical Results〔J〕.IEEE Trans on Power Delivery，1990，5(3):1 568-1 574.

〔16〕胡敏，陈元.配电系统最优网络重构的模拟退火算法〔J〕.电力系统自动化，1994，18(2):24-28.

〔17〕陈国良，王煦法，庄镇泉，等.遗传算法及其应用〔M〕.北京:人民邮电出版社，1996.

〔18〕M.A.Kashem，GBJasmon，V.Ganapathy.A new approach of distribution system Reconfiguration for loss minimization〔J〕. Electric power and energy systems，2000(22):269-276.

〔19〕王超学，崔杜武，崔颖安，等.使用基于中医思想的蚁群算法求解配电网重构〔J〕.中国电机工程学报，2008，28(7): 13-18.

〔20〕王超学，李昌华，崔杜武，等.一种新的求解配电网重构问题的免疫遗传算法〔J〕.电网技术，2008，32(13):25-30.

〔21〕杨建军，战红，刘杨.基于环路和改进遗传算法的配电网络重构优化〔J〕.高电压技术，2007，33(5):109-113.

〔22〕He S，Wu Q H，A novel group search optimizer inspired by animal behavioral ecology〔J〕.2006 IEEE CongressEvolutionary Computation，Vancouver，Canada，2006.

〔23〕He S，Wu Q H，Saunders J R.Group search optimizer:an optimization algorithm inspired by animal searching behavior〔J〕. IEEE Trans on Evolution Computation，2009，13(5):973-990.

〔24〕李鹏.基于群搜索优化算法的配电网重构〔D〕.长沙:湖南大学，2011.

〔25〕董百强.基于禁忌搜索算法的配电网重构的研究〔D〕.重庆:重庆大学，2006.

〔26〕 Lin C H，Chen C S，Wu C J，etal.Application of immune algorithm tooptimalswitchingoperation fordistribution-loss minimisation and loading balance〔J〕.IEE Proceedings of Generation，Transmission and Distribution，2003，150(2): 183-189.

〔27〕RAO R S，NARSAIMHAM S V L，RAMALINGARAJU M，et al.Optimal network reconfiguration of large-scale distribution system using harmony search algorithm〔J〕.IEEE Trans on Power System，2011，26(3):1 080-1 088.

〔28〕陈春，汪枫，刘蓓，等.基于基本环矩阵与改进和声搜索算法的配电网重构〔J〕.电力系统自动化，2014，38(6): 55-60.

〔29〕林海源，李晓明，余平.基于支路交换和模拟退火的配电网重构算法〔J〕.华东电力，2004，32(11):3-7.

〔30〕卢耀川，廖迎晨，陈星莺，等.基于遗传退火法的网络重构技术〔J〕.电力自动化设备，2003，23(1):28-31.

〔31〕陈曦.基于协同进化算法的配电网重构研究〔D〕.上海:上海交通大学，2008.

〔32〕沈广，陈允平，刘栋.基于最小生成树编码的配电网恢复遗传算法〔J〕.电力系统自动化，2007，31(14):81-84.

〔33〕陈雁，孙海顺，文劲宇，等.改进粒子群算法在船舶电力系统网络重构中的应用〔J〕.电力自动化设备，2011，31(3): 29-34.

Summary on the network reconfiguration algorithms for smart distribution grids

ZHU Jiran1，LENG Hua1，TANG Haiguo1，ZHANG Runxian2，GONG Hanyang1，LI Longgui2
(1.State Grid Hunan Electric Power Corporation Research Institute，Changsha 410007，China；2.Hunan University，Changsha 410082，China)

The paper introduces the common algorithms and research situations at home and abroad of distribution network reconfiguration.Not only the advantages and disadvantages of all kinds of algorithms and application scenarios are analyzed，but also combination of these algorithms and detail optimization on improving reconfiguration effect are emphasized.

smart；distribution network；network reconfiguration；mathematical optimization；heuristic；artificial intelligence；algorithm

TM711.1

A

1008-0198(2015)06-0001-05

10.3969/j.issn.1008-0198.2015.06.001

2015-09-01