一种基于度排序的节点重要性排序算法

张玫,解建军,冯科展

（1.河北师范大学数学与信息科学学院,河北石家庄050024；2.河北省计算数学与应用重点实验室,河北石家庄050024）

一种基于度排序的节点重要性排序算法

张玫1,2,解建军1,2,冯科展1,2

（1.河北师范大学数学与信息科学学院,河北石家庄050024；2.河北省计算数学与应用重点实验室,河北石家庄050024）

为有效评估复杂网络中节点的重要性,特提出了一种基于经典度排序方法的合度排序算法.合度排序算法是在节点度的基础上提出了邻度和合度的概念,通过计算每个节点的合度值来评估节点在网络中的重要性,即合度值越大,节点在网络中的重要性越高.并利用经典的度排序算法、接近度排序算法及新提出的合度排序算法对同一网络拓扑图的节点进行排序,证明了合度排序算法的有效性.

复杂网络；节点重要性；度；排序

自从17世纪瑞士科学家Euler研究七桥问题开始,很多学科的科研人员也都尝试利用图论知识开展研究,其中包括社会科学、生命科学、信息科学等.无论是人类社会网络、牲畜群网络还是Web互联网,它们都是由众多复杂的节点和连接方式构成的庞大网络,都属于复杂网络[1].通过对复杂网络的分析研究,得出与实际问题相关的规律,从而应用到解决实际问题中去.例如人类社会关系网络[2],通过节点排序可以迅速找到某个人,这与著名的“六度分离（six degrees of separation）”实验[3]类似；利用谣言传播网络[4],可以挖掘出始作俑者,从而切断谣言传播途径；通过世界航空网络[5],可以迅速找出到达目的地的最合适路径等.那么,如何定量地分析网络中节点的重要性就成为复杂网络研究的一个重要方面.经典的度排序算法存在着不足,本文从如何解决这一问题入手,受复杂网络中熟人免疫机制的启发,在考虑节点自身度值的同时,也将邻居节点的度值加入考虑的范畴,从而极大地提升了网络中节点排序的准确性.

1 经典的节点重要性排序算法

评估网络中节点重要性的算法有很多,大多都是根据节点或节点之间的连边来进行考虑的.下面首先介绍度排序算法与接近度排序算法.

度排序,简而言之就是根据网络中每个节点度值的大小进行排序的算法[6].度大的节点则在该网络中的地位比较重要,度越小的节点越不重要.比如在铁路网中,车站代表节点,两城市之间若有开通列车,则存在连边,那么某节点的连边越多,说明该城市的列车开往的城市越多,该点的地位也越重要.若网络为无权的完全图,那么网络中存在条边,计算网络中所有节点度的时间复杂度为O（N2）,利用快速排序算法对节点度排序,时间复杂度为O（NlogN）,因此度排序算法时间复杂度为O（N2+NlogN）,式中N为网络中节点的数目.该方法能以较低的算法复杂度从一定程度上计算出复杂网络中节点的重要性,但是此方法也存在明显的缺点.如图1所示网络中,节点5的度数虽小于节点4和节点6,但它是连接两个子网络的关键,因此不能简单地仅用节点的度来衡量节点的重要性.

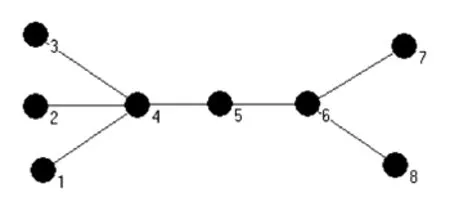
图1 网络拓扑Fig.1 Network topology

接近度CLi的计算公式为其中d（Vi,Vj）表示以节点Vi为起点,节点Vj为终点的最短路径长度.那么接近度越大的节点在网络中所处位置也越接近中心,接近度越小的节点越靠近网络的边缘[7].若计算两节点之间的最短路径长度采用Dijstra算法,时间复杂度为O（N2）,同样利用快速排序算法对各节点的接近度值进行排序,那么接近度算法的时间复杂度为O（N3+NlogN）.接近度排序算法不仅考虑了节点的度值,还考虑了节点在网络中所处的位置,以此算法对节点的重要性进行判断比较准确.

2 度排序的改进算法

2.1 网络模型

本文研究的复杂网络均为无向无权网络.假设网络G有N个节点,M条边,则V={V1,V2,V3,…,Vn},代表顶点的集合,E={E1,E2,E3,…,Em}代表网络中边的集合,网络G中各节点之间的关系用邻接矩阵A=[aij]来表示,其中

定义1（度）顶点Vi的度是和Vi相关联的边的数目,记为TD（Vi）.

定义2（邻度）对于网络G中的一个节点Vi,G中所有与Vi相邻的节点的度的总和称为节点Vi的邻度,记为Ni.

定义3（合度）对于网络G中的一个节点Vi,其邻度与节点自身度值之和称为节点Vi的合度,记为Bi,即2.2 合度排序算法

合度排序算法的基本思路是将网络中节点自身的度值与其所有邻居节点度值之和相加,进而利用所得数据作为分析节点重要性的评估依据.

根据上面的定义,可以给出复杂网络中节点重要性的合度排序算法：

若网络为无权的完全图,则步骤（1）和步骤（2）的时间复杂度均为O（N2）,步骤（3）和步骤（4）的时间复杂度均为O（N）,步骤（5）的时间复杂度为O（NlogN）,那么合度排序算法的时间复杂度为O（N2+ NlogN）.

通过上述对合度排序算法的性能分析,其时间复杂度与度排序算法相同,优于接近度排序算法.另外,合度排序算法与度排序算法相比,不仅考虑了节点的度,还考虑了节点之间的联系,因此与传统的度排序算法相比具有准确性上的优势.

3 算例

以一个简单的复杂网络G（见图2）为例,利用合度排序算法对网络G中节点的重要性进行排序.首先叙述合度排序算法的执行过程,并通过结果验证该算法的有效性及准确性.

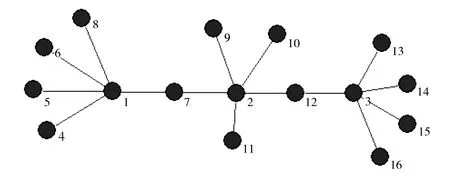
图2 复杂网络GFig.2 Complex network G

以节点2为例,首先计算节点2的邻度.节点2的邻居节点7、9、10、11、12的度值分别为2、1、1、1、2,节点2的邻度值就是将节点7、9、10、11、12的度值相加,为7.那么,节点2的合度值就是将节点2自身的度值加上其邻度值,即5+7=12.

根据合度排序算法计算出的网络G中各节点的度值、邻度值以及计算获得的合度值如表1所示.

表1 节点参数Tab.1 Node parameter

由表1可知,根据合度值对该网络中节点进行排序,结果为：2,7,12,1,3,4,5,6,8,9,10,11,13,14,15,16.为了说明此算法的有效性,利用度排序算法和比较准确且常用的接近度算法作比较,结果如表2所示.

表2 与经典算法的比较结果Tab.2 Comparison with classical algorithms

由表2可知,度排序只考虑了节点自身度值,未考虑节点与节点之间的联系,因此将节点度值一样的节点1,2,3排在了首位,而将分别连接两个子网络的节点7和节点12排在了后面.本文提出的合度排序算法与经典的接近度算法对网络G中节点的重要性排序结果完全一样,将位于网络中心的节点2排在了首位,有连接作用的节点7和节点12紧随其后,其次是位于边缘两个子网络的节点1和节点3,对于11个叶子节点,3种排序算法都是一样的.这个结果证实了合度排序算法的有效性.

4 小结

节点的重要性排序是复杂网络的研究重点,对于复杂网络的研究有十分重要的意义.本文在总结复杂网络节点重要性排序算法的基础上,对度排序算法进行改进,将节点度值扩大化,兼顾了节点与节点之间的联系,使排序结果更准确有效.同时,较之经典的接近度排序算法具有更小的时间复杂度等优点,而且更直观地评估了节点的重要性.下一步将利用合度排序算法针对复杂网络的抗毁性评估及防护策略展开研究[8].

[1]汪小帆,李翔,陈关荣.复杂网络理论及其应用[M].北京：清华大学出版社,2006.

[2]Wasserman S,Faust K.Social network analysis：methods and applications[M].Cambridge：Cambridge University Press,1994.

[3]Milgram S.The small world problem[J].Psychology Today,1967（5）：60-67.

[4]Zanette D H.Dynamics of rumor propagation on small-world networks[J].Phys Rev,E,2002,65：041908.

[5]高峰,党亚茹.世界航空客运网络的节点度分布特征[J].科学学与科学技术管理,2009（7）：75-79.

[6]司晓静.复杂网络中节点重要性排序的研究[D].西安：西安电子科技大学,2012.

[7]陈静,孙林夫.复杂网络中节点重要度评估[J].西南交通大学学报,2009,44（3）：426-429.

[8]Albert R,Jeong H,Barabási A L.Error and attack tolerance of complex networks[J].Nature,2000,406：378-382.

（责任编辑：卢奇）

A method about node importance evaluation based on degree-rank

Zhang Mei1,2,Xie Jianjun1,2,Feng Kezhan1,2
（1.College of Mathematics and Information Science,Hebei Normal University,Shijiazhuang 050024, China；2.Key Laboratory of Computational Mathematics and Applications,Shijiazhuang 050024,China）

To effectively evaluate the importance of nodes in complex networks,a both degree sorting algorithm based on the classical degree sorting algorithm was proposed in this paper.Both degree sorting algorithm is proposed the concept of neighbor degree and both degree on the basis of the concept of node degree,through the calculation of both degree of each node to evaluate the importance of the nodes in the network,the higher the value of both degree, the more important position in the network.And by using the classical degree sorting and closeness sorting algorithms, and the new proposed both degree sorting algorithm on the same network topology node sorting,proving the validity of the proposed sorting algorithm.

complex network；node importance；degree；sorting

O157.5

A

：1008-7516（2015）02-0061-05

10.3969/j.issn.1008-7516.2015.02.014

2015-01-14

河北省自然科学基金项目（A2014205027）；河北师范大学应用开发基金项目（L2015K01）

张玫（1989―）,女,河北磁县人,硕士研究生.主要从事复杂网络、信息安全研究.

解建军（1971―）,男,山西运城人,副教授,硕士生导师.主要从事信息安全研究.