某水电站库区边坡监测线性回归方程的建立及分析

张立银

(中国电建集团西北勘测设计研究院有限公司，西安 710065)

某水电站库区边坡监测线性回归方程的建立及分析

张立银

(中国电建集团西北勘测设计研究院有限公司，西安 710065)

在边坡的变形监测数据分析中，可以依据任意抽取的某一时段的监测样本数据做出变量间关系的散点图和变量之间关系的回归线，它能够最理想地反映监测数据变量间的关系。以抽取的2个变量的一批测量数据作为样本数据，建立变量之间回归方程，并对这一回归方程进行检验，以确定其能否比较可靠地反映2个变量之间的关系，如果回归方程可靠，就可通过回归计算的结果，对边坡位移量趋势进行分析，从而掌握变形体变形的动态和特征，对被预测变量进行有效的预测。

边坡；样本数据；线性回归方程；相关系数；判定系数；变形分析

0 前 言

某水电站变形边坡地段位于电站库区右岸，岸顶高程距大坝500～1 500 m,正常蓄水位高程时距大坝900 ～1 700 m，由于该边坡变形范围大、距离大坝近、规模大，其稳定性对工程安全影响较大，一旦变形体发生较大规模的失稳，产生高的滑速，涌浪将严重威胁坝体及相关设施的安全。为了较详细地分析边坡变形范围、不同部位变形的差异，为边坡的变形分区、稳定性评价以及监测预警提供依据，根据坡体的变形特征，先后布置了大量的监测点进行了较系统的监测工作。系统的变形监测点部分布置在坡体顶部平台部位，主要按3个剖面布置。

1 线性回归方程的建立

由于在变形体上布置的监测点数量较多，且监测次数也很多，所以本文选择了变形量较大的2号剖面上的3个点QC7-2、LS04、IP10-1作为样本对象，抽取第179～198次监测时段的20组水平位移累计数据作为数据样本，进行线性回归方程的建立和分析。

1.1 监测点布置及监测数据

变形监测点样本水平位移数据，见表1。监测点布置及监测散点的趋势见图1、2。

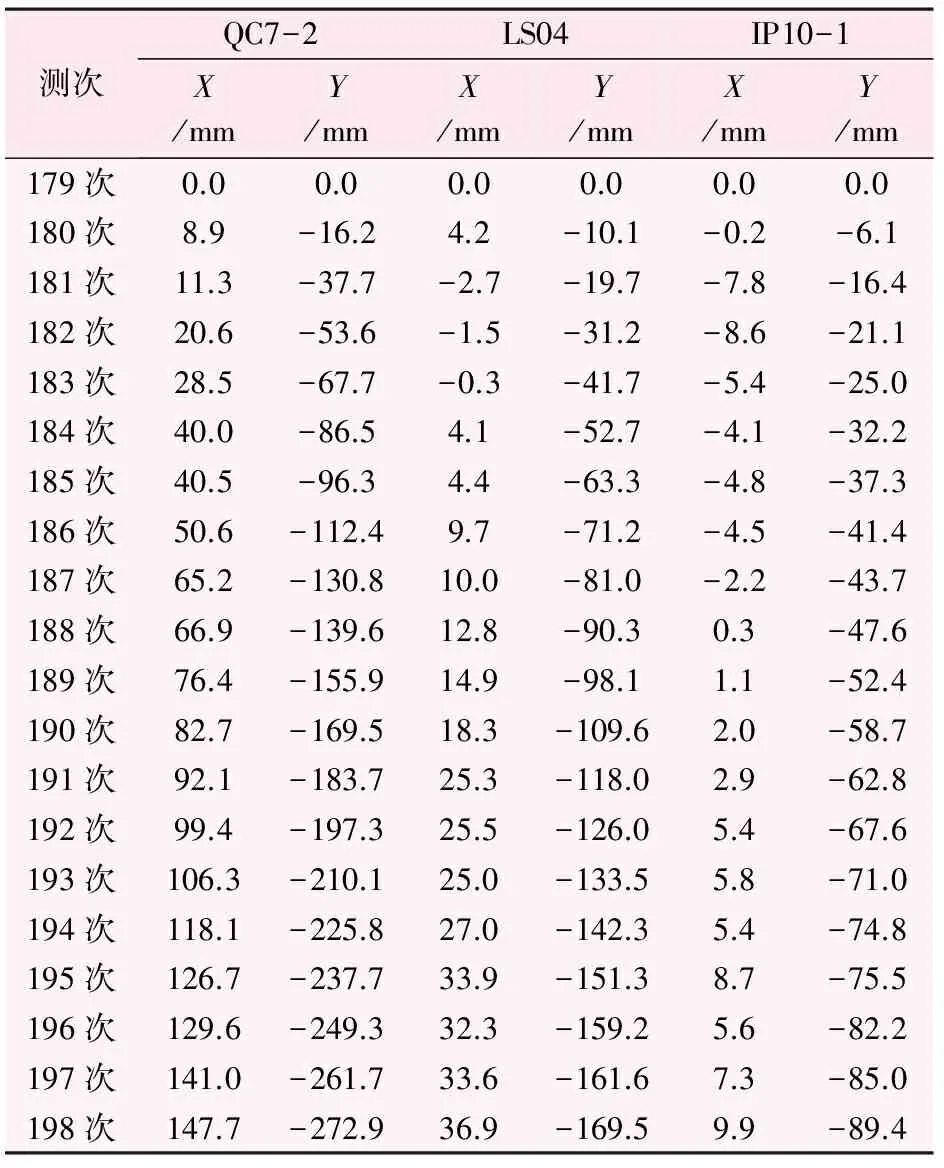
表1 变形监测点样本水平位移数据表

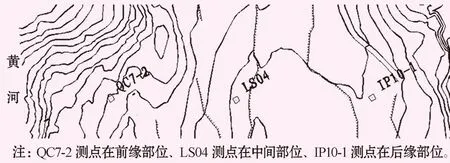
图1 变形体3号剖面监测点布置图

1.2 线性回归方程的计算

将表1监测点的水平位移样本数据代入以下公式，分别计算各点的回归系数a和b的拟合值，可求得各测点的线性回归方程。

(1) QC7-2测点的线性回归方程

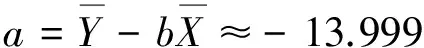
QC7-2测点的回归方程为：

Y=a+bX=-13.999-1.807X

(2) 同理求得LS04的线性回归方程

Y=-30.579-3.889X

(3)IP10-1的线性回归方程

Y=-46.166-3.980X

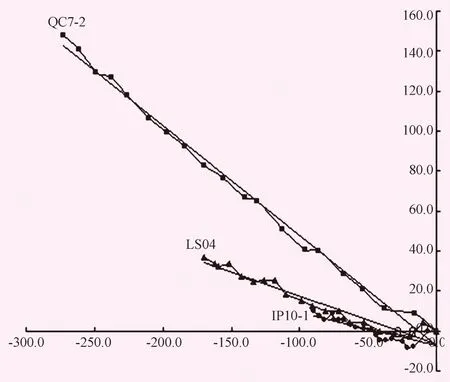
图2 监测点散点及趋势图

1.3 线性回归模型的显著性检验

从总体中随机抽取部分样本，根据样本的20组X与Y的资料导出以上线性回归模型，变量Y值是否有效，必须通过显著性检验才可作出结论。本文只对上述回归系数b进行检验。回归系数b是决定X与Y变量依存关系形式的重要参数。如果b= 0 说明X与Y不存在线性关系。因此检验总体回归系数b= 0 的假设就等于检验总体X与Y变量有没有线性关系的假设。因为本文抽取的样本数量较小，所以我们用标准化处理t变量。此t变量服从自由度为n-2 的t分布，可以查t表确定临界值。

(1) QC7-2测点的线性回归方程模型的显著性检验

假设H0∶b=0、H1∶b≠ 0,并设显著性水平a=0.05,已知样本QC7-2回归系数b=-1.807,则样本回归系数b的标准误差为:

得出：

|t|=|b|/ξb=55.015

查t表得t0.05(20-2)=2.101,t值超过临界值，所以拒绝原假设，说明样本的回归系数b是显著的，即不能否定QC7-2测点的线性回归方程模型X与Y变量存在线性关系。

(2) 同理求得LS04的线性回归方程的 |t|=|b|/ξb=16.193。

(3)IP10-1的线性回归方程的|t|=|b|/ξb=6.048。

它们的t值均超过临界值，所以拒绝原假设，线性回归方程模型X与Y变量存在线性关系。

2 线性回归方程的相关系数r及判定系数r2的计算

2.1 相关系数r

(1) 测点QC7-2线性回归方程相关系数r的计算，由下列公式得出：

=-0.997

(2) 同理求得LS04测点线性回归方程相关系数r的值为:r=-0.967。

(3) IP10-1测点线性回归方程相关系数r的值为:r=-0.819。

2.2 判定系数r2

我们由上述1.2节求得的回归直线方程,确定了X和Y的具体变动关系, 但是实际值是不是紧密分布在其两侧？其紧密程度如何？这关系到回归模型的应用值。因此，对回归直线的拟合优度必须加以测定，判定系数r2便是测定直线回归模型拟合优度的一个重要指标。

(1) 测点QC7-2线性回归方程判定系数r2的计算，通常采用以下简捷公式计算得：

(2) 同理求得LS04测点线性回归方程判定系数r2的值为:r2=0.935。

(3) IP10-1测点线性回归方程判定系数r2的值为:r2=0.670。

3 测点变形分析

我们通过以上回归计算的结果，对选择的3个监测点QC7-2、LS04、IP10-1样本对象进行水平累计位移量趋势的分析。

3.1 从线性回归模型的显著性检验分析

通过对3个监测点的线性回归模型的显著性检验，我们计算出的3个t值关系为：

|tQC7-2| >|tLS04|>|tIP10-1|

可以看出3个监测点样本的t值逐渐减小，说明回归系数b的显著性也就随之减小，即，X与Y变量存在的线性关系逐渐减弱。

3.2 从相关系数r分析

由2.1节所计算出的3个样本监测点的相关系数r值的关系为:

|rQC7-2| >|rLS04|>|rIP10-1|

因为r表示2组数据线性相关的程度，从另一方面度量了点相对于标准差的散布情况。相关系数r的范围在[-1,1]之间，r的值越接近正负1，说明(x,y)越靠拢趋势线，数据相关性也越强；r的值越接近0，说明(x,y)点到趋势线的散度越大，数据相关性越小。

从3个样本监测点的r值关系可以看出，r的绝对值接近1的程度由大变小，说明点到趋势线的分散度变大，数据相关性变小。

3.3 从判定系数r2分析

与r值的关系相同，3个样本监测点的判定系数r2关系如下：

因为判定系数r2是测定直线回归模型拟合优度的一个重要指标，它是以回归偏差占总偏差的比率来表示回归模型拟合优度的评价指标。

由2.2节计算结果表明，QC7-2、LS04、IP10-1三个测点的Y的总偏差中分别有99.4%、93.5%、67.0%可以由X同Y的依存关系来解释，只有0.6%、6.5%、33.0%属于随机因素的影响，说明实际值紧密分布在回归直线两侧，随机因素的影响很小，因此它们的回归线是合适的。从3个测点的r2的关系看出，直线回归模型拟合优度由强变弱，即，分布在趋势线两侧的点的紧密程度由大变小。

3.4 综合分析

从上述几种回归计算的数据分析中得出的结论是一致的，那就是该变形体整体处于变形状态，而且从该变形体上所选择的位于2号剖面上的3个样本测点的回归计算结果表明，该监测剖面的变形特征是：各监测点的水平累计位移量从平台前缘至后缘逐渐减小，即，从平台前缘至后缘变形体的变形程度是由强变弱的。从图2也能看出，从平台后缘至前缘，各点的水平累计位移曲线从趋于平缓到明显变陡，斜率增大。而且水平累计位移曲线长度最短的是后缘点IP10-1，其次是中间部位的测点LS04，最长的是前缘QC7-2测点，且各监测点的位移曲线基本呈直线状，这些就说明各测点的绝对位移量有所不同，但可认为各点的变化是匀速的，也就是说变形体处于匀速变形状态，这与前面的回归计算分析结果相符，说明以上分析是有效的。

4 结 语

本文利用线性回归模型的建立及分析的基本原理，引入随机抽取的边坡监测的数据样本，并以此实例进行线性回归模型的建立及分析，通过对实例的计算，掌握了该变形体变形的动态特征，较好地描述了各测点的变化规律。验证了该变形体变形剧烈且匀速。回归方程模型是一种对数据变化趋势做出正确分析的模型，本文通过实例计算分析，证实线性回归方程在此变形体监测上的应用是有效的。

[1] David Freedman,(美)著.统计学[M]. 魏宗舒，译.北京：中国统计出版社,1999.

[2] 中国水电顾问集团西北勘测设计研究院.该电站滑坡段监测成果分析及失稳预测研究[R].西安：2012.

[3] 宋爱斌.数理统计理论、应用与软件实现[M].北京:国防工业出版社，2012.

[4] 邱卫宁.测量数据处理理论与方法[M].武汉:武汉大学出版社，2008.

[5] 张述清，徐巍，薛小攀，周泽阳.虎家崖水电站前池高边坡综合治理监测成果分析[J].西北水电,2012,(02):109-122.

[6] 王福昌.最小一乘回归系数估计及其 MATLAB 实现[J].防灾科技学院学报, 2007,(12):85-89.

Establishment and Analysis of Linear Regression Equation for Slope Monitoring

ZHANG Li-yin

(POWERCHINA Xibei Engineering Co., Ltd., Xi'an 710065,China)

In analysis on the deformation monitoring data of the slope, scatter diagram and regression line of relationship between variables can be drawn respectively in accordance with the data of the monitoring samples taken randomly at one period. They can ideally reflect the relationship between the monitoring data variables. Based on one batch of the monitoring data of two variables as the sample data, the regression equation between the variables is established. Meanwhile, this regression equation is verified to secure it can reliably reflect the relationship between the two variables. Provided that the regression equation is reliable, tendency of the slope displacement can be analyzed by application of the results of the regression calculation. Accordingly, development and characteristics of the deformation of the deformation mass can be learnt and the effective prediction can be performed to the variable to be predicated.

slope; sample data; linear regression equation; correlation coefficient; judgment coefficient; deformation analysis

1006—2610(2015)02—0016—04

2014-12-23

张立银(1963- )，男，甘肃省永登县人,高级工程师，主要从事工程测量工作.

TV698.17

A

10.3969/j.issn.1006-2610.2015.02.005