新建下穿路基对既有铁路桥桩基附加沉降的计算方法

郭　剑

(中铁工程设计咨询集团有限公司，北京　100055)

A Calculation Method of Settlement of Railway Bridge Pile Foundation Caused by Newly-constructed Roadbed Below

GUO Jian

新建下穿路基对既有铁路桥桩基附加沉降的计算方法

郭剑

(中铁工程设计咨询集团有限公司，北京100055)

A Calculation Method of Settlement of Railway Bridge Pile Foundation Caused by Newly-constructed Roadbed Below

GUO Jian

摘要介绍一种用于求解新建路基引起既有铁路桥附加沉降的方法。通过对基于Boussinesq解的等代墩基法、线弹性土-等代墩基界面模型、荷载传递法以及现行规范公式的系统化综合，借助矩阵对运算数据进行整理，进行迭代运算，得到新建铁路路基下穿既有铁路桥梁时路基填土对既有桥梁桩基础的附加沉降。以山西中南部铁路工程某实际工点为算例，演示其计算过程。

关键词等代墩基法Boussinesq解荷载传递法线弹性土-等代墩基界面模型沉降

近年来，随着铁路建设的发展，新建铁路与既有铁路交叉的情况越来越频见。新建铁路与既有铁路交叉时，多采用自既有线下方下穿通过，部分新线选择自既有线桥下通过。既有铁路桥经多年运营，其桩基础沉降多进入稳定期，而附近新建路基后，可造成桩基的二次附加沉降。国内各类关于地基、基础的规范和专著中，均缺少对此种情况计算方法的介绍(国标地基与基础规范中仅有地面堆载对扩大基础影响计算，未对桩基础的影响进行规定[1])，且国内各种期刊上很少见到对此类问题的深入研究。实际工程应用中通常依靠工程经验对此情况进行定性讨论，或综合其他因素，一并划定安全间距等。鉴于此，寻找一种符合现行规范及经典论著的计算方法，以对新建路基造成的临近既有铁路桥桩基附加沉降量进行计算，具有比较现实的意义。

1路基接触应力及计算荷载面、界面的划分

路基基底接触应力计算[2]：按照常用的计算方法，有比例荷载法及均布荷载法，还有研究者提出采用弹性土堤法[3]更接近于实测情况[4]。由于计算基准面位于地面以下，摩擦桩基底埋深通常较大，压缩层更位于该高度以下，根据圣维南原理，三种算法只要合力一致，等代墩基底的附加应力分布应当一致，出于简单起见，采用均布荷载法。

根据《铁路桥涵地基与基础》中空间弹性问题平面荷载的基本解算思路[5]，将路基平面荷载划分为i×j块，界面I、界面I′，划分为k×l块，两个界面II，各划分为k×l块(与I面及I′面数量不一致)，并将路基基底均布荷载简化为每一块形心处的一个集中荷载(如图1)。

图1　荷载面及土-等代墩基界面

2起算基准面及桩基沉降计算方法的选取

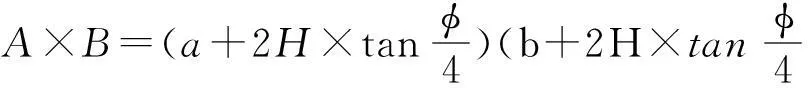
3土-等代墩基传递荷载的计算

首先，在弹性范畴内对等代墩基底部土层的附加应力及周围土层的竖向位移求解，可采用Boussinesq解[7，11]；其次，由于既有铁路桥修建时间较早，沉降已稳定，且该荷载不卸除，可认为该处土体处于正常固结，可认为后加的地面堆载使等代墩基周围的土体发生了沉降，可按照荷载传递法[7]的原理，土体与等代墩基之间的沉降位移差以摩阻力的形式作用于等代墩基的四周。土-等代墩基界面采用线弹性模型，极限摩阻力取规范值，并按各层土厚度进行加权平均[8，12]。据统计，弹性极限相对位移可取10mm，即相对位移在10mm之内为线弹性规律，超过10mm后取其极限摩阻力[7，10]，即堆载后桩基沉降的荷载分为两部分。

(1)堆载通过土体传递直接作用于桩底土的荷载计算[5，9]

(1)

式中B1——路基底面半宽；

x——新建线路中心至桥墩中心距离；

z——计算点的深度。

(2)堆载通过土体、土-等代墩基界面、等代墩基后间接作用于桩底土的荷载计算

可先取一个土-等代墩基界面，不妨可先取I面。对此界面上某单元块，按照

(2)

可计算出各荷载单元块(i×j个)形心与其形心的距离

依次算出k×l个界面单元的Rij值，组成矩阵

对矩阵中各元素按照如下公式[7]

(2)

求解界面处各单元块中心处的竖向位移。

uz——界面单元块中心处竖向位移；

Q——荷载面单元块中心处等效集中荷载，取路基基底接触应力乘以荷载面分块面积；

R——界面单元块中心至各荷载面单元块中心的距离；

z——界面单元块中心处竖向坐标；

μ——土的泊松比；

E——土的弹性模量。

由于采用线弹性的土体模型，因此各荷载单元块引起某一界面单元的位移可以叠加，即对各个界面单元块的uz，ij进行相加，得到各个界面单元块中心点处的竖向位移值为

(4)

此时，即可得到I面处各单元块中心点位移矩阵[uz]k×l。矩阵中各元素再减去等代墩基相应处的沉降量后，得到相对位移矩阵[Δuz]k×l。首次计算中，等代墩基各处沉降量为0，在随后的迭代运算中，可将上次算得的沉降值带入。按照土-等代墩基线弹性界面模型[7，10]，即

(5)

以fkl乘以各个单元块的面积，得到各单元块处界面单元作用于等代墩基表面的力矩阵[f]k×l，将各元素相加，得到I面总的竖向力

(6)

同样，以相同的方法可求得I′面处的力FI′及两个II面处的力FII。最后对各界面处的竖向力进行相加，F=FI+FI′+2FII，将此竖向力除以等代墩基底面积，得到间接荷载

(7)

将此荷载与等代墩基底处由土体直接传递来的竖向荷载相加，得等代墩基底面处总荷载为

(8)

按照规范公式[8]

(9)

计算等代墩基的沉降量S。将此沉降量继续代入位移矩阵[uz]k×l中重新计算相对位移矩阵[Δuz]k×l，迭代计算后，直至沉降量所需的荷载与两部分荷载之和一致，即得到最终结果。

4工程实例

4.1　工程概况

某新建单线铁路自山西中南部铁路某特大桥下通过。在穿越点处，新建线顶面宽度6.8 m，高度6.4 m，路基边坡按照1∶1.5放坡，坡脚处宽度26.5 m，容重18 kN/m3，截面积为106.6 m2，垂直穿越既有铁路桥。新建线路中心距离临近桥墩中心13.84 m。工点处为洪泛区，地质情况为成层的冲洪积黏土，粉质黏土及粉、细砂，各层加权内摩擦角φ=17.8°，水位线在地面以下5.3 m，邻近的既有线桥墩高度13 m。该墩两侧桥跨度均为32 m，采用9根φ1.0 m的桩，承台尺寸为9.7 m×7.5 m×3.0 m，桩外缘尺寸为6.4 m×8.6 m，桩长40 m，等效墩基A×B=14.83 m×12.63 m，桩底置于深厚的硬塑黏土层中，基本承载力200 kPa。工点处相对情况及各层土钻探情况分别见图2及表1。

底层土土工试验结果见表2。

图2　新建路基及既有铁路桥梁相交(单位：cm)

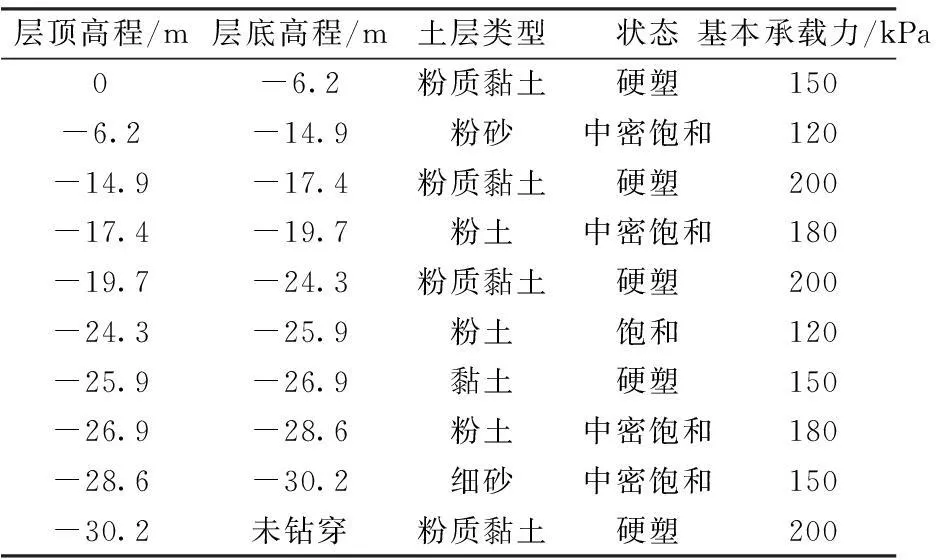
层顶高程/m层底高程/m土层类型状态基本承载力/kPa0-6.2粉质黏土硬塑150-6.2-14.9粉砂中密饱和120-14.9-17.4粉质黏土硬塑200-17.4-19.7粉土中密饱和180-19.7-24.3粉质黏土硬塑200-24.3-25.9粉土饱和120-25.9-26.9黏土硬塑150-26.9-28.6粉土中密饱和180-28.6-30.2细砂中密饱和150-30.2未钻穿粉质黏土硬塑200

注：地面点高程取为相对高程0.0 m。

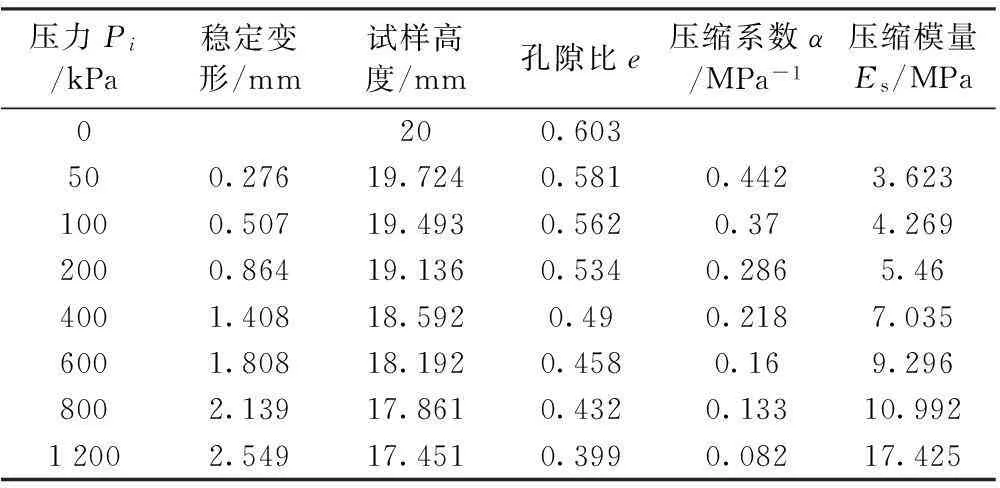
表2　底层土土工试验结果

底层土e～P曲线及Es～P曲线见图3及图4。

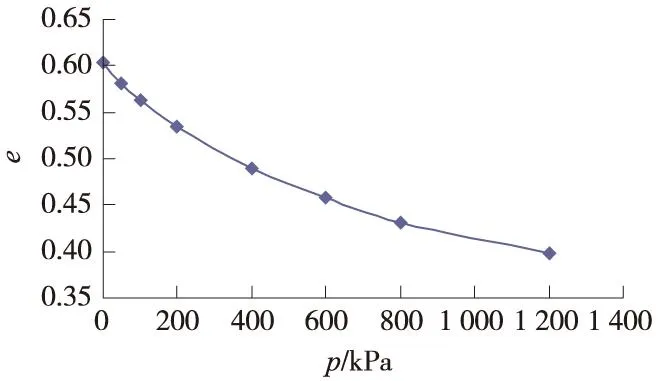
图3　底层土e～P曲线

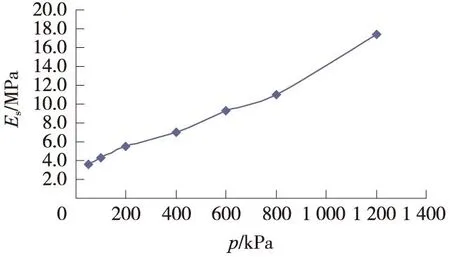
图4　底层土Es～P曲线

4.2　计算过程

(1)路基基底接触应力计算及荷载面、界面划分

按照均布荷载法，以截面积106.6 m3乘以容重18 kN/m3，加上轨道恒载58.9 kN/m后，除以底面宽度，算得路基底面应力为86.7 kPa。 将路基基底荷载划分为i×j=26×86=2 236个单元块(路基长度取不小于6倍等代墩基相应宽度，取86 m)，界面I、界面I′，均划分为k×l=43×14=602块，两个界面II，各划分为k×l=43×12=516块，荷载作用平面及土-等代墩基界面近似划分的小块均约为1 m×1 m。

(2)新建路基堆载通过土体传递直接作用于桩底土的荷载的计算

(3)堆载通过土体、土-等代墩基界面、等代墩基后间接作用于桩底土的荷载计算

按照上述方法，依次结算出[R]26×86、[R26×86]43×14、[uz，26×86]43×14及[uz]43×14，其中，Q=78.7 kN，μ=0.25、E=43 MPa(μ及E为经各层加权平均[5])。矩阵中各元素再减去等代墩基相应处的沉降量后，得到相对位移矩阵[Δuz]43×14。按照土-等代墩基线弹性界面模型(式5)，取f为规范值，并进行各层加权平均，得f=45 kPa/10 mm[8]，

5结论

通过以上方法，填补了既有桥受新建路基的附加沉降无定量计算方法的空白，在工程实际中，可参考此方法的计算结果制定对应的措施。在解算中，可看出该方法所有的解算依据与参数取值均以既有规范及经典理论为依据，其计算结果有一定的参考价值，且其所用的参数在常规勘测设计过程中较为常见，也便于在勘测设计过程中应用。需要注意的是，本方法综合的各种经典理论中，多数为基于正常固结土的前提，不适用于超、欠固结土。在迭代运算过程中，由于f值相对较大，因此F的收敛性较差，通常需要进行手工多次输入计算，以使沉降量所需荷载与传递的荷载一致。在该解算过程中，仅仅利用了土-等代墩基的竖向位移与土层的平均极限位移之差，以及用加权平均极限摩阻力求解其竖向力。在勘测过程中，如能应用钻孔剪切试验[10]，测定各土层的极限位移、极限摩阻力及残余抗剪强度，用以对土-等代墩基的界面模型进行优化，则能得到更有意义的结果。

参考文献

[1]中华人民共和国住房和城乡建设部，中华人民共和国国家质量监督检验检疫总局.GB50007—2011建筑地基基础设计规范[S].北京：中国建筑工业出版社，2012

[2]蒋关鲁，王海龙，李安洪.高速铁路路基基底应力计算方法[J].铁道建筑，2009(4)：65-69

[3]Perloff W H， Baladi G Y. Stress distribution within and under long elastic embankments[J]. Highway Research Record， 1967(181):12-40

[4]温特科恩 H F.基础工程手册[M].钱鸿缙，叶书麟,译.北京：中国建筑工业出版社，1983

[5]铁道部第三勘察设计院.桥涵地基和基础[M].北京：中国铁道出版社，2002

[6]中华人民共和国住房和城乡建设部.JGJ94—2008建筑桩基技术规范[S].北京：中国建筑工业出版社，2008

[7]张忠苗.桩基工程[M].北京：中国建筑工业出版社，2007

[8]中华人民共和国铁道部.TB10002.5—2005铁路桥涵地基和基础设计规范[S].北京：中国铁道出版社，2005

[9]刘成宇.土力学[M].北京：中国铁道出版社，2005

[10]李广信.高等土力学[M].北京：清华大学出版社，2004

[11]张夫健.铁路桥梁群桩基础沉降性状与计算分析[J].铁道勘察，2012(3)：75-77

[12]刘明宇.非饱和黏性土压缩模量与标贯击数关系探讨[J].铁道勘察，2012(3)：41-43

中图分类号：TU434

文献标识码：B

文章编号：1672-7479(2015)02-0032-04

作者简介：郭剑(1984—)，男，2009年毕业于北京交通大学桥梁工程专业，工程师。

收稿日期：2014-12-22