基于可靠度理论的水工结构设计方法

肖黎莎 张瑞刚康 海 李欢欢

（1.中国水利水电第八工程局有限公司 长沙市 410004；2.重庆交通大学水利水运工程教育部重点实验室 重庆市400070；3.重庆市万盛经济技术开发区水务局 重庆市 400800；4.中山大学 广州市 510275）

结构可靠性是研究结构在各种随机因素作用下的安全问题。应用可靠性理论可以解决结构的强度、刚度、稳定性等问题。该理论以概率论、数理统计方法和随机过程理论为基础，从系统角度出发，将结构系统的设计、分析、评价、检测和维护融为一体[1]。随着计算机技术的发展，结构可靠度已从科学理论研究发展到了广泛应用阶段[2-3]，目前它已在水利、航空、机械、土建等领域得到应用。

在进行水工结构的设计时，过去多采用单一安全系数等方法，具有简单、明了、概念明确的优点，在工程实际应用中也已积累了丰富的经验，实践证明这一方法是基本可行的。可是，这种设计方法实际上是用定数模型来处理不确定性问题，本身在理论上存在着不足，这也就使得该方法不能较好地评价水工结构或边坡结构的稳定程度、真实的安全状态[4]。

水利工程中的坝体结构可靠或不可靠是受各种外界及自身内部随机因素影响的。结构绝对可靠是不可能的，只能说其失效概率极小。为了使结构设计更为可靠，国家先后颁布了《水利水电工程结构可靠度设计统一标准》（GB50199-94），及《水工混凝土结构设计规范》（SL/T191-96）等规范，以期打破过去水利水电技术标准采用传统的单一安全系数的做法，将可靠性理论得以推广[5-6]。其后，发布了《水工混凝土结构设计规范》（SL191-2008）、《水利水电工程结构可靠性设计统一标准》（GB50199-2013）等规范性文件，对旧的设计规范进行替换，可靠度理论在水利设计中逐渐趋于方便与快捷。同时，周新刚、GuoL、赵国藩等学者结合有限体积法(FVM)、蒙特卡罗等方法对结构耐久可靠度进行了模拟研究以及阐述了国外结构可靠性的研究进展[7-9],但是在研究过程中，多集中于某项实验分析，与目前国内采用的设计规范对比性不足，因此本文结合我国现行规范对水工结构设计中的可靠度方法展开研究。

1 水利工程结构可靠度计算模型

根据《水利水电工程结构可靠性设计统一标准》（GB50199-2013）等规范性文件，目前水工结构可靠度的分析计算主要采用“作用效应—结构抗力”计算模型或在其基础上进行变化的模型。根据可靠性的定义，结构失效之后即不可靠。因此，在明确结构功能和失效模式条件下，结构可靠度就可定量地表示[10]：若结构抗力小于施加在它上面的作用效应，结构就失效，此事件发生的概率即为失效概率。

基于此，定义如下：作用效应用S表示，其为非负随机变量或随机过程；结构抗力用R表示，也为非负随机变量或随机过程；当作用效应S不超过结构抗力R时，结构被认为是可靠的,否则,被认为是失效的。用数学方程表示为：

（1）结构处于可靠状态，结构的工作状态未超过阈值，结构处于安全、实用状态，此时R-S>0；

（2）结构处于极限状态，结构的工作状态达到了极限承载能力状态，此时R-S=0；

（3）结构处于失效状态，结构的工作状态超过阈值，结构会产生断裂、不安全变形等，此时R-S<0。

可得到判断结构可靠性的功能函数，水工结构设计的可靠性思维要点便是需满足此函数取值要求，这种设计思路也称为结构可靠度设计。在水工结构中，R反映的是坝体材料本身的力学特性，S反映的是整个坝体所受到的外荷载作用。

2 水工结构的可靠度分析

以重力坝为例，在不同的工况下，其破坏主要考虑两种方式，即强度破坏和稳定破坏，对应的可靠度则称为强度可靠度和稳定可靠度[3]。

（1）水工结构的稳定性可靠度分析。水工结构的抗滑稳定性计算是基于承载能力极限状态进行的。以重力坝为例进行分析，重力坝是依靠自身重量产生的抗滑力来维持其稳定性。重力坝计算中认为滑动面为胶结面，重力坝坝体为刚体[3,11]。此时滑动面上的滑动力作为效应函数，阻滑力为抗力函数。由此可得到坝基面抗滑稳定极限状态的方程：

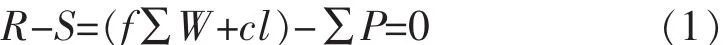
式中 f——基岩抗剪摩擦系数；

c——基岩抗剪断内聚力；

l——坝基的宽度；

∑W——计算界面上全部荷载的铅直分力总和；

∑P——水平力的总和。

但是我们在设计过程中不难发现水工结构的极限状态都较为复杂，使用不便，因此在SL/T191-96中采用了以概率理论为基础的极限状态设计方法。以可靠指标度量结构的可靠性，从而建立起极限状态与结构可靠度之间的数学关系。该可靠度方法引入了两种极限状态（承载能力极限状态、正常使用极限状态）、3种荷载 （永久荷载、可变荷载、偶然荷载）、3种安全级别、5种分项系数等。分项系数的选择需考虑工程结构安全级别、设计状况、作用和材料性能的变异性、计算模式不定性等。从而对水工结构最终应达到的可靠度水平进行设计。对坝工而言，分项系数是依据坝体结构的重要性、坝高、失效后果、破坏性质、经济指标等因素以优化方法分析并结合工程经验而确定的[11]。分项系数极限状态设计法概念明确、使用简便。

例如,对于承载能力极限状态,按作用效应基本组合,其设计表达式为:

式中 Sd（·）——作用组合的效应（永久荷载、可变荷载等）设计值函数；

Rd（·）——结构抗力设计值函数;

γ0——结构重要性系数；

Ψ——设计状况系数；

γdn——相应第n种作用组合的结构系数；

Gk——永久作用的标准值;

γG——永久荷载的分项系数；

Qk——可变作用的标准值;

γQ——可变荷载的分项系数；

ak——几何参数的标准值。

但是在使用过程中，仍有不少人反映SL/T191-96分项系数过多，比较繁琐，使用仍然存在不方便，希望采用更为简便的单一系数方法。因此在SL 191-2008中将γ0、γdn、Ψ合并为一个系数K，也即承载力安全系数K，则可将承载能力极限状态简化成为KS≤R，此时传统的单一安全系数设计法与考虑分项系数的可靠度方法得到了较好的结合，实现了由复杂到简单的进化[12]。

（2）水工结构的强度可靠度计算。仍然以重力坝为例，混凝土重力坝的材料强度对保证大坝安全十分重要。混凝土具有的抗压强度高的特点，重力坝正是充分利用这个特点发挥其效益。基于强度可靠性方法，以计算重力坝上游、下游边缘的垂直应力为例，可得到：

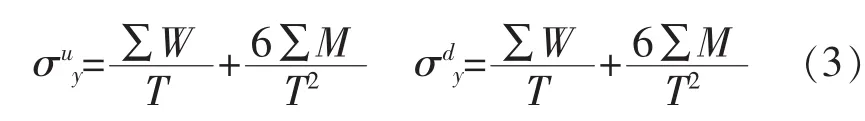
T——坝底宽度（m）；

∑W——计算界面上全部荷载的铅直分力总和，以向下为正（kN）；

∑M——计算截面上全部荷载对计算截面形心力矩总和，逆时针方向为正（kN/m）。

通过这种计算方法，可得到坝体材料应力值，但其应力值需满足DL5108-1999《混凝土重力坝设计规范》规定的强度指标。此时则满足R>S。

同理，考虑分项系数的可靠度理论设计方法表达式为：

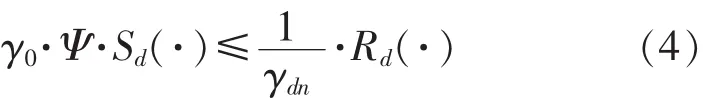
据此，同样可以依据概率极限状态设计法，计算得到设计值。

3 可靠度计算中的系数取值

如前文所述，由于过去分项系数过多，新规范SL191-2008中采用了多系数分析，安全系数表达的方法，各系数的选取如下[13]：

（1）设计状况系数Ψ。新规范SL191.2008中考虑到施工阶段发生事故的概率较高，对基本组合，取设计状况系数Ψ为1.0；对偶然组合，取为0.85。

（2）结构重要性系数γ0。SL/T191-96将水工结构的安全级别分为Ⅰ、Ⅱ、Ⅲ级，结构的重要性系数取为1.1、1.0、0.9。对于四五级建筑物，在大中型水利水电工程的4、5级水工建筑物结构重要性系数取0.9显然偏低，故提高至0.95。在SL191-2008中，计算承载力安全系数K值时，将4、5级建筑物的结构重要性系数γ0取0.95，1、2、3级建筑物的结构重要性系数仍取为1.1和1.0。

（3）结构系数γd。配筋混凝土的结构系数γd取为1.2；素混凝土的结构系数γd按受拉破坏和受压破坏分别取为2.0和1.3。

将以上系数Ψ、γ0、γd代入K=Ψγ0γd中，则可以得到K值，取整后得到规范SL191-2008文献[12]中表3.2.4混凝土结构构件的承载力安全系数取值表。

4 结论及建议

（1）本文根据《水利水电工程结构可靠性设计统一标准》（GB50199-2013）等规范性文件，对目前水工结构可靠度的“作用效应-结构抗力”分析计算模型进行分析；基于对坝基面抗滑稳定分析及混凝土重力坝的材料强度极限状态分析，发现采用以概率理论为基础的极限状态设计方法更为简便。基于此，对照规范 《水工混凝土结构设计规范》（SL/T 191-96）及（SL191-2008）将可靠度理论应用于水工结构稳定性计算。基于设计规范，对可靠度方法中各系数取值进行研究，使传统的单一安全系数设计法与考虑分项系数的可靠度方法得到了较好的结合，将复杂计算方法简单化。

（2）考虑可靠度理论的设计方法已成为当代国际工程结构领域的发展趋势，可靠度理论在水工设计中的应用关键在于合理地确定分项系数，我国目前使用的设计规范中系数取值多按经验选取，并未按统计学方法取值。建议完善荷载和材料等参数数据库，加强对参数均值及变异系数等原始数据的整合，从而使分项系数取值更为合理。

（3）传统的单一安全系数法和可靠度设计中的分项系数法各有优缺点，建议进一步研究两种表达系数之间的关系，从而建立一种表达式简单、概念明确的概率极限状态设计法。

[1]吴世伟.结构安全度与可靠度分析论文集 [C].江苏:河海大学出版社，1988.

[2]A.M.Freudenthal,J.M.Garrelts,etal.The analysis of structural safety[J].ASCE，1947，（112）:267-325.

[3]王婷.混凝土重力坝的可靠性分析[D].阜新：辽宁工程技术大学，2005.

[4]李清富，高建磊，乐金朝.工程可靠性原理 [M].郑州：黄河水利出版社，1995.

[5]GB50199-94.水利水电工程结构可靠度设计统一标准[S].北京：中国计划出版社，1994.

[6]SL/T191-96.水工混凝土结构设计规范[S].北京：中国水利水电出版社，1996.

[7]周新刚，夏辉，李克非.基于FVM数值分析的海工混凝土结构耐久可靠度MonteCarlo模拟[J].工程力学，2014，31（9）:166-173.

[8] Chen T， Gao X W.Transient meshless boundary element method for prediction of chloride diffusion in concrete with time dependent nonlinear coefficients [J].Engineering Analysis with Boundary Elements，2012，36（2）: 104-111.

[9]贡金鑫，赵国藩.国外结构可靠性理论的应用与发展[J].土木工程学报，2005，38（2）:1-7.

[10]哀文阳，何金平，李正农，等.坝工设计的可靠性思维[J].中国农村水利水电，1996，（8）:16-18，48.

[11]蒋春艳，常晓林，周伟.用于重力坝抗滑稳定分析的分项系数有限元方法[J].水力发电学报，2006，（2）:16-20.

[12]SL191-2008.水工混凝土结构设计规范[S].北京：中国水利水电出版社，2008.

[13]刘志明，雷兴顺.可靠度设计方法在水利技术标准中的应用[J].中国水利，2009，（20）:45-48.