基于小波变换的图像融合算法研究*
任敏善
(91913部队 大连 116041)
基于小波变换的图像融合算法研究*
任敏善
(91913部队 大连 116041)
为解决单源图像无法全面准确捕捉信息的问题,提出了一种基于小波变换的图像融合算法。首先,将多源图像进行多层小波分解,得到各个图像的低频信息和高频信息。接着对小波系数采用像素点区域特征的融合规则进行融合处理,最后通过小波逆变换得到重构图像。仿真结果表明,融合后的图像低频信息部分并没有发生改变,而高频细节部分融合了两幅源图片中的细节部分,使得融合后的图片更加清晰,可信度更高。
小波变换; Mallat算法; 图像融合; 融合规则
Class Number TP391.41
1 引言
图像融合是数据融合的一个非常重要的分支,是20世纪70年代后期提出的概念,是综合了传感器、图像处理、信号处理、计算机和人工智能的现在高新技术[1~2]。图像融合的主要思想是采用一定的算法,把工作于不同波长范围、具有不同成像机理的图像传感器对同一个场景的多个成像信息融合成一个新图像。多源融合图像比单源图像具有更多的优势,因为多源图像具有冗余性,具有单源图像无法捕捉的信息,因此多源融合图像能够从多个视点获取信息,扩大时空的传感范围,提高观测的准确性和鲁棒性[3~6]。
小波变换是相对较新的概念,20世纪80年代前后才提出小波变换的概念,它是在傅里叶变换的基础上发展起来的,在图像处理、模式识别、机器人视觉、量子力学等领域得到广泛应用。本文提出了基于小波变换的图像融合算法,并对融合结果进行了分析,融合后的图像可信度更高,模糊更少,可理解性更好,更适合人的视觉及计算机检测、分类、识别、理解等处理。
2 小波变换及Mallat算法
2.1 小波变换定义[7]
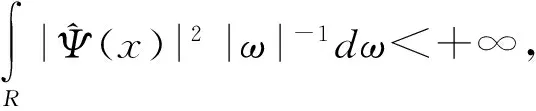
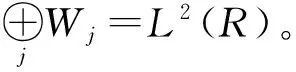
2.2 小波快速算法(Mallat算法)
尺度函数和小波函数是小波理论的核心,二尺度差分方程是空间逐级二剖分赋予尺度函数和小波函数的最基本性质。设φ∈V0∈V1,故存在一序列{hk}∈l2,使尺度方程满足
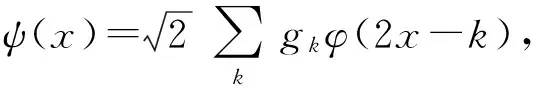
并且hk和j的具体指无关,无论对哪两个相邻级其值都相同。从二尺度差分方程出发可以得到小波变换的快速算法,即Mallat算法[8]。
2.3 用于图像处理的二维小波变换
由于图像是二维信号,因此,需要将小波变换由一维推广到二维。重构过程也可以类似的由一维推广到二维,对于给定的尺度函数和小波系数,对二维图像C(m,n)的小波分解为
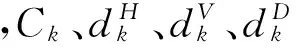
3 基于小波变换的图像融合方法
3.1 融合方法
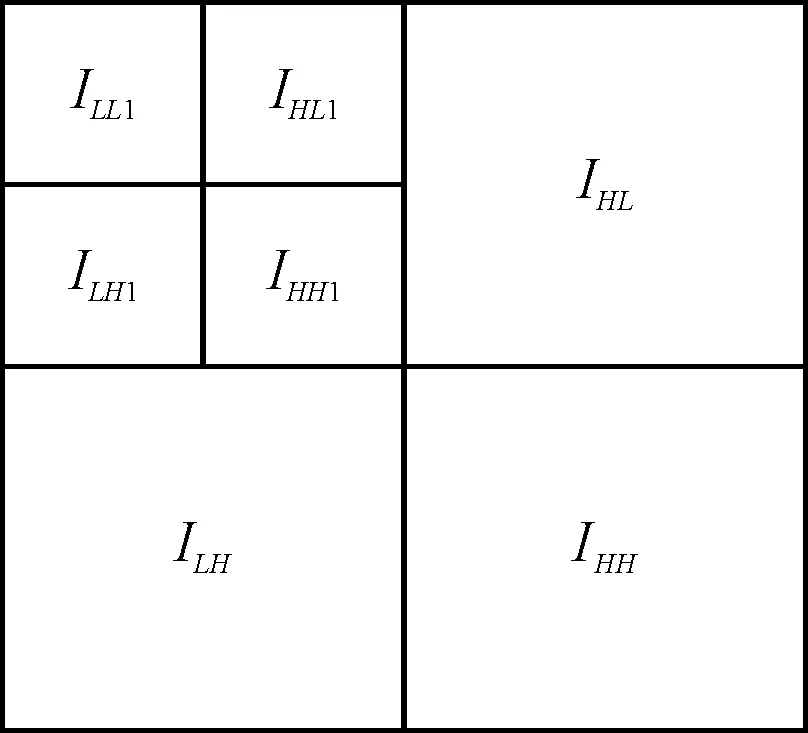
图1 两层图像小波分解图
根据多分辨率小波快速分解和重建理论,可以对图像进行多层次分解,每一层分解产生四幅子图像ILL、ILH、IHL、IHH。图1所示为一个两层分解的图像,其中ILL集中了原始图像中主要低频部分,ILH对应垂直方向高频信息,IHL对应水平方向高频信息,IHH对应着对角线方向的高频信息。小波分解的层数越高,对应层的图像尺寸就越小。对于图像而言,小波变换是将图像分解成频域上各个频率段的子图像,以代表源图的各个特征分量。这对后续的融合极为重要。
基于小波变换的图像融合流程如下图所示,融合的基本步骤如下:
1) 对参与融合的两幅源图像A、B进行配准;
2) 对参加融合的每一幅源图像分别进行小波分解,得到图像的小波系数;
3) 对各分阶层分别进行融合处理,对各分阶层的小波系数按照融合规则进行融合处理,得到融合后的小波系数;
4) 对融合后得到的小波系数进行小波逆变换进行图像重构,形成融合后的图像F。
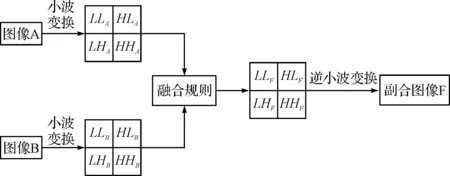
图2 基于小波变换的图像融合流程图
3.2 融合规则
设计融合规则的理论基础是:小波变换后低频波段表征图像的近似部分,而高频波段表征图像的细节信息,高频波段的系数在零值左右波动,系数的绝对值越大,表示该处亮度变化激烈,即可能包含图像的重要信息,如边缘、线条以及区域边界。根据小波变换后图像的特征,根据各自的特点可以将其大致分为三类:基于单像素点的规则、基于像素点区域特征的规则和基于图像全局特性。
1) 基于单像素点的规则
这类算法主要有:基于绝对值最大值选取的(即挑选欲融合,每一个位置上具有最大绝对值的小波系数到融合图像的相应位置处)、基于加权平均的和直接对高频部分替换或追加的。
2) 基于像素点区域特征的规则
基于区域特征的融合规则的基本思想是:在对某一分解层图像进行融合处理时,为了确定融合后的像素,不仅要考虑参加融合图像中对应的各像素,而且要考虑参加融合像素的局部区域。具体做法是将某位置处区域的方差、能量、梯度、距离等特征作为一种测度来指导该位置处的系数选取,区域大小一般取3*3、5*5、7*7的窗口。以区域能量测度的融合规则为例,其融合方法过程如下:
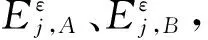
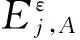
(2)计算两幅图像对应方向、对应分辨率上局部区域的匹配度
(3)确定融合算子
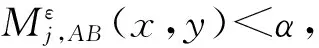

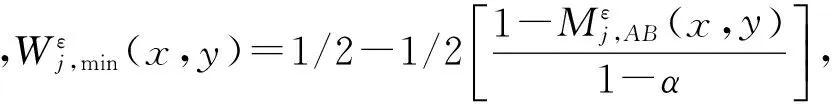
3) 基于图像感兴趣区域或目标的规则
这种算法将特征层融合和像素层融合结合在一起,以图像分割的结果指导像素层融合,采用这种基于区域的融合规则关键在于:将每个像素看成感兴趣区域或目标的一部分;利用图像特征,如边缘和区域来指导融合;从小波系数中重新得到空域和频域信息。
4 信息建模及融合结果
4.1 信息建模
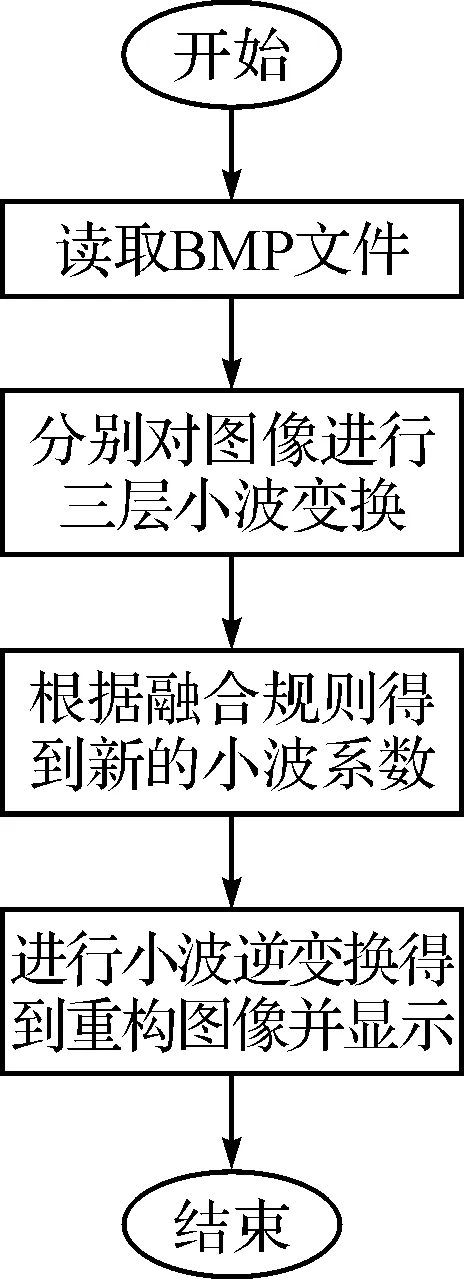
图3 图像融合程序流程图
图像融合的程序流程图如图3所示,在融合过程中,对多源图像分别进行三层小波变换,得到相应的高频信息和低频信息。根据基于像素点区域特征的融合规则,对每一层的小波系数进行进行融合,得到新的小波系数。再对其进行小波逆变换得到融合后的图像。
图像的小波变换具有分辨率信息,那么在系数融合中,应采取同尺度下的绝对值比较判断。例如在融合频带LL过程中,为了完好地保存图像的特征信息,避免融合后图像特征的损失,绝对值比较采用邻域处理的方法。比较W1(i,j)和W2(i,j)过程中,分别在各自的变换系数中取3*3的邻域(实际程序中采用了7*7的邻域)处理的方法,假设:
若Rs1 4.2 程序仿真与分析 为了对基于小波变换的图像融合效果进行分析,选取了两幅已经配准好且像素位宽一致的两幅图像(灰度级均为0~255,且图像的大小均为720×480pixel)进行图像融合。 图4 融合前的两幅图像 两幅图像的高频细节部分不同,而低频信息部分两幅图像基本一致。因此,图像融合所要做的便是将两幅图中的细节部分整合到一幅图像中去,同时又不能丢失图像信息部分,程序运行得到的结果如下: 图5 融合后的图像效果 通过对比观察可以看到,融合后的图像低频信息部分并没有发生改变,而高频细节部分融合了两幅源图片中的细节部分,使得得到的图像更加的清晰。融合后的图像可信度更高,模糊更少,可理解性更好,更适合人的视觉及计算机检测、分类、识别、理解等处理。 针对单源图像无法全面准确捕捉信息的问题,提出了一种基于小波变换的图像融合算法。对图像进行小波分解后,根据高频分量和低频分量的特点,选取了相同大小的区域但以不同阈值来对图像进行融合,仿真结果表明使用该算法得到的融合图像可信度更高,模糊更少,可理解性更好,更适合人的视觉及计算机检测、分类、识别、理解等处理。 [1] 韩崇昭,朱红艳,段战胜.多源信息融合[M].北京:清华大学出版社,2006:27-33. [2] Jamie T, Uwe A. Information fusion in the immune system[J]. Information Fusion,2010,11(7):35-44. [3] Maslov I V, Gertner I. Multi-sensor fusion: an evolutionary algorithm approach[J]. Information Fusion,2006,7(3):304-330. [4] Durrant-Whyte H F, Stevens M, Nettleton E. Data fusion in decentralized sensing networks[C]//Proceedings of the Fourth International Conference on Information Fusion, Montreal, Canada,2001:302-307. [5] Xiong N, Svensson P. Multi-sensor management for information fusion: issues and approaches[J]. Information Fusion,2002,3(2):163-186. [6] 林卉,杜培军.基于小波变换的遥感影像融合与评价[J].电子技术应用,2005,4(1):36-39. [7] 彭玉华.小波变换与工程应用[M].北京:科学出版社,2002:19-67. [8] 刘桂雄,林旭虹.基于CMAC的图像融合快速算法[J].光学精密工程,2008,16(5):950-956. [9] Balaras C A, Argiriou A A. Infrared thermography for building diagnostics[J]. Energy and Buildings,2002,34(2):171-178. [10] Clark M R, MaCann D M, Forde M C. Application of infrared thermography to the non-destructive testing of concrete and masonry briges[J]. NDT and E International,2003,26(4):265-269. An Image Fusion Algorithm Based on Wavelet Transform REN Minshan (No. 91913 Troops of PLA, Dalian 116041) To solve the problem that the single source image can not fully and accurately capture information, an image fusion algorithm based on wavelet transform is proposed. Firstly, the multi-layer wavelet decomposition of the multi-source images are made, from which high frequency and low frequency coefficients are obtained. Secondly, the wavelet coefficients are processed using the fusion rule of the pixel wavelet coefficients. Finally, the reconstructed image is gained by inverse wavelet transform. The experimental result shows that, the low frequency of the reconstructed image is not changed, while the high frequency is more exhaustive than both of images. So the reconstructed image is more clear and more reliable. wavelet transform, Mallat algorithm, image fusion, fusion rule 2014年10月7日, 2014年11月27日 任敏善,男,工程师,研究方向:图像处理和雷达信号处理。 TP391.41 10.3969/j.issn1672-9730.2015.04.012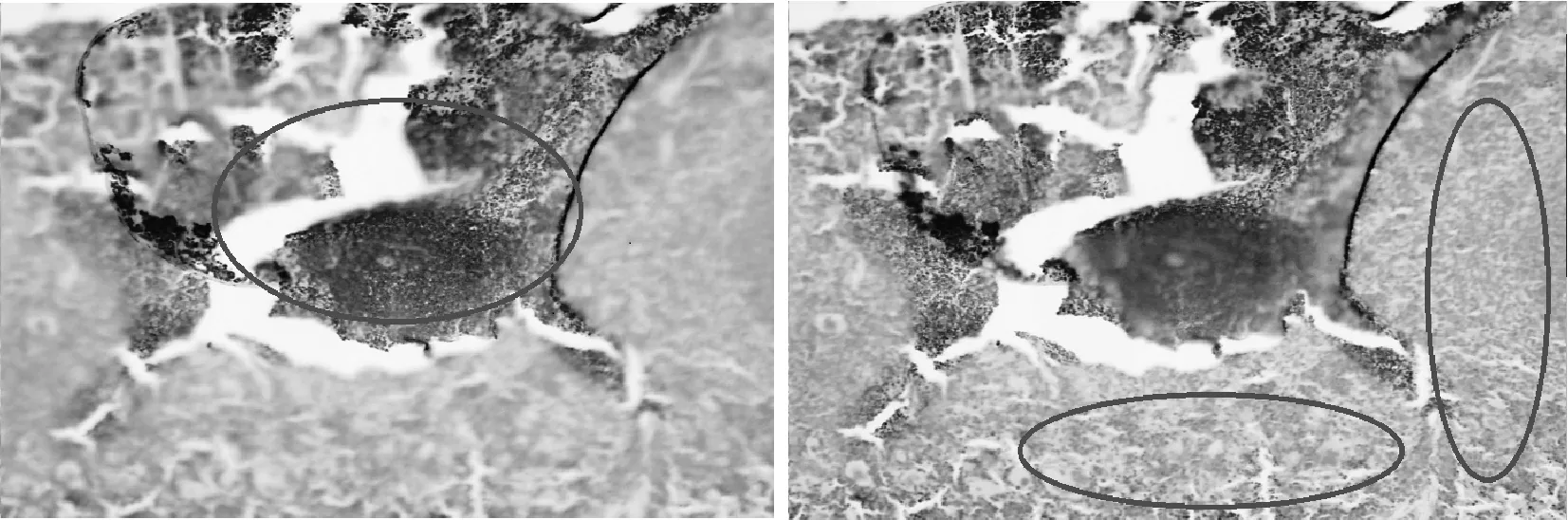

5 结语

