改进K均值聚类法在变压器故障诊断中的应用
王 莹 卢秀和
(长春工业大学,吉林 长春130012)
0 引言
电力变压器是电力系统中非常重要的枢纽电气设备,其正常运行是电力系统安全运行与稳定的前提,所以准确、有效地进行变压器故障诊断显得尤为重要。油溶气体分析(DGA)技术[1]中改良三比值法是近年来常用的变压器故障诊断方法,但由于变压器的多种故障类型与改良三比值法中特征气体组分含量之间的关系存在一定的模糊性和不确定性,导致改良三比值法在变压器故障诊断中存在一定的不足[2]。为此需对DGA技术的改良三比值法中有关变压器故障的多种数据进行研究,而聚类分析法是研究和挖掘数据的主要方法[3]之一,为此分析改良三比值法的特征气体三对比值之间的数据关系,采用改进K均值聚类法对变压器进行故障诊断,从而进一步提高电力变压器故障判断的精准性。
1 聚类分析
聚类[4]就是按照不同事物间所具有的某种相异性对事物进行分类和划分的过程,该过程属于无监督分类,没有先验知识和教师指导,而是通过不同事物间相异程度(可用距离表示)来进行。而聚类分析则是融进了数学方法,对采集到的数据集进行分类的一种分析。聚类算法按照聚类的方式、准则和分类结果的取值方法分为很多种,本文采用按聚类准则分类中的K均值聚类分析(简称K均值)和改进K均值聚类分析(简称改进K均值)来进行变压器故障诊断。
2 K均值聚类算法
K均值算法先随机选取K个对象作为初始聚类中心,然后计算每个对象与各个聚类中心的距离。算法步骤如下:
(1)K均值算法使用聚类准则函数为误差平方和准则Jc:返回(2);否则算法结束。
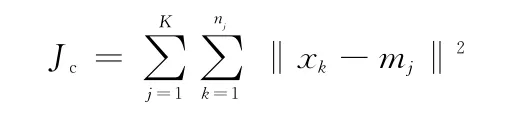
为使聚类结果优化,应使准则Jc最小。
(2)采集n个样本,令I=1,表示迭代次数,选取K个初始聚合中心Zj(1),j=1,2,…,K。
(3)计算每个样本与聚合中心的距离D[xk,Zj(I)],k=1,2,…,n;j=1,2,…,K。若。
(4)计算K个新聚类中心:

(5)判断:若Zj(I+1)≠Zj(I),j=1,2,…,K,则I=I+1,
K均值进行初始分类时,先随机选一批代表点,然后依次计算其他样本归类。先计算第一个样本,把它归于最近的一类,形成新的分类。然后计算新聚类中心,再计算第二个样本到新聚类中心距离,对第二个样本进行归类,依次类推。
3 改进K均值聚类算法
K均值受初始值影响很大,不同初始点选择会导致不同结果,改进K均值算法对K均值算法的初始聚类中心选择方法进行了改进,从数据对象分布出发动态地寻找并确定初始聚类中心点。本文采用基于最小距离的初始聚类中心选取法[5]进行改进K均值的初始聚类中心点确定,然后再利用K均值进行运算。
4 K均值聚类和改进K均值聚类MATLAB实现
在MATLAB中,调用如下程序可实现K均值聚类:[IDX,C,SUMD,D]=kmeans(data,K)。其中,IDX为聚类结果;C为聚类中心;SUMD为每一行样本到该聚类中心距离和;D为每一个样本到各个聚类中心距离;data为要聚类的数据集合,每一行为一个样本;K为分类个数。
样本数据选取改良三比值法的三对特征气体的比值作为三个样本特征值,即x=C2H2/C2H4、y=CH4/H2、z=C2H4/C2H6,选择变压器故障中的四种故障作为划分类别,即低温过热、中温过热、高温过热和低能放电,分别编号为1、2、3、4。样本数据如表1所示。

表" 样本数据
利用K均值算法和改进K均值算法MATLAB仿真图如图1和图2所示。

图" ;均值聚类算法分析图

图- 改进;均值聚类算法分析图
5 结论与分析
本文在改良三比值法的基础上利用改进K均值算法将采集到的14组变压器样本数据进行正确的分类和识别,实现了变压器故障的诊断。
由图1和图2对比可以看出,14个点中有一个蓝色点偏离很大,这是由于不同的初始点对K均值算法的分类和识别结果影响很大,K均值算法不能完全将14组样本数据良好地分类识别。而改进K均值算法可以很好地对14组样本数据进行判别和分类。由表1可以看出,改进K均值算法弥补了K 均值算法对编号3和4无法良好识别的缺陷。
二者结果图和表的对比,进一步验证了改进K均值算法在变压器故障诊断中的准确性、可行性和有效性。
[1]高文胜,严璋,谈克熊.基于油中溶解气体分析的电力变压器绝缘故障诊断方法[J].电工电能新技术,2000,19(1):22-26.
[2]彭宁云.基于DGA技术的变压器故障智能诊断系统研究[D].武汉:武汉大学,2004.
[3]陈舵.模糊聚类分析及其在电力变压器故障诊断中的应用研究[D].西安:西安理工大学,2008.
[4]王子建.模糊聚类分析及其在变压器油色谱数据分析中的应用[D].武汉:华中科技大学,2006.
[5]周润景,张丽娜.基于MATLAB与fuzzyTECH的模糊与神经网络设计[M].北京:电子工业出版社,2010.

