放松管制环境下基于改进布谷鸟搜索算法的DGO与DNO效益均衡模型

陈政，曾鸣，张翔，常启诚，欧鹏，，宋艺航，钱琪琪，欧阳邵杰，刘英新

(1.南方电网科学研究院，广州市 510080；2.华北电力大学经济与管理学院，北京市 102206；3.北京邮电大学，北京市 100876)



放松管制环境下基于改进布谷鸟搜索算法的DGO与DNO效益均衡模型

陈政1，曾鸣2，张翔1，常启诚3，欧鹏1，2，宋艺航1，钱琪琪2，欧阳邵杰2，刘英新2

(1.南方电网科学研究院，广州市 510080；2.华北电力大学经济与管理学院，北京市 102206；3.北京邮电大学，北京市 100876)

近年来，分布式发电以其节能、环保等特点发展快速。然而在分布式发电接入配电网的过程中，会对配电网运营商(distribution network operators，DNO)的利益造成影响，从而阻碍两者的协调发展。为了兼顾配电网运营商与分布式发电商(distributed generation owners，DGO)的利益，研究了分布式发电投资及配电网建设规划的联合优化问题。在构建目标函数过程中引入利润分配系数从而达到双赢目的，同时需要满足配电网安全稳定运营及减排目标约束。对于模型中存在的不确定性因素使用两点估计法进行确定，使用改进的布谷鸟搜索算法求解所建模型。最后以IEEE33节点配电系统为例，通过不同情境之间的对比分析验证了所提出方法的有效性和可行性。

放松管制；效益均衡；分布式发电商；配电网运营商；改进的布谷鸟搜索算法

0 引 言

分布式电源是指直接布置在配电网或分布在负荷附近的小容量发电设施[1-3]。随着集中发电、远距离输电和大电网互联的弊端不断显现，常规发电成本增加，以及人们环保意识不断增强，分布式发电(distributed generation，DG)越来越受到关注[4]。然而，分布式发电接入配电网，会改变配电线路中的电力潮流，对配电网的规划运行，乃至安全效益和经济效益都会带来一定影响。在放松管制的市场环境下，分布式发电的投资和运营决策是由分布式发电商(distributed generation owners，DGO)决定的，而保证电网安全可靠运行是配电网运营商(distribution network operators，DNO)的责任。在此背景下，分布式发电的投资运行对DNO会带来怎样的影响，如何引导DGO和DNO合理规划、科学决策，使得两者利益能够兼顾并增加社会总福利，是值得研究的问题。

由于分布式发电优化配置与配电网规划息息相关，当前研究分布式发电与配电网规划的相关文献按照决策变量的类型可以分为单一规划和综合协调规划2类：(1)在不改变系统馈线和变电站配置的情况下，对分布式发电的安装位置和容量进行优化，如张惠卿等[5]使用改进的多种群遗传算法解决分布式发电选址和定容问题，崔艳龙[6]考虑配电网运行的经济性和安全性建立了分布式发电的单一规划模型；(2)分布式发电与配电网变电站或馈线等的整体规划，是一种全局优化规划，李振文[7]综合考虑分布式发电的选址定容和配网网架规划，研究了计及分布式发电的配电网扩展规划模型，文献[8]研究了考虑用户侧的微型分布式发电的配电网发展规划。

分布式发电优化配置的计算模型可以分为单目标优化和多目标优化2种。单目标优化又可以分为3类：从投资角度，以供电公司年总规划成本现值最小为优化目标[9]；从损耗角度，以配电网损最小为优化目标[10]；从环保效益角度，以分布式发电安装容量最大为优化目标[11]。多目标约束如张立梅等[12]考虑分布式电源的投资成本、卖电收益、环境改善,以及网损、电压质量、可靠性和延缓网络更新等，建立了分布式电源单位成本收益和其接入后改善电网所得收益最大化的多目标规划模型；张惠卿等[5]使用分布式发电投资成本最小、网损最小和静态电压稳定裕度最大建立多目标优化模型。然而上述情况大多只从某一方的经济利益最优为目标函数建立优化模型，没有考虑DNO与DGO之间存在的利益关系及其在分布式发电和配电网规划过程中可能造成的影响，缺乏对DNO和DGO之间的利益协调机制进行研究，而这正是本文研究的重点。

本文通过建立DNO和DGO之间的利益协调优化模型，旨在解决不同类型分布式发电机组(在本文所考虑的机组类型中只包含分布式风力发电一种具有出力不确定性的可再生能源)和配电网的联合规划问题，属于全局优化模型。在优化目标设定时本文创新性的将DNO和DGO的各自利润通过利益分配有机的融合在一起，同时在约束条件中加入了减排约束，并使用改进的布谷鸟搜索算法(improved multi-objective shuffled frog leaping algorithm，IMO-SLFA)对所建立模型进行求解，试图寻求一个双赢的考虑DGO利益的配电网规划方案。最后以IEEE-33节点系统为例进行多情景分析，验证文中所建模型的有效性和实用性。

1 模型构建

1.1 目标函数

DNO和DGO是市场利益链中的两个主体，既联系紧密又存在利益矛盾，若仅仅重视某一方的利益必然导致市场效率的下降。因此，鉴于DNO和DGO在进行投资决策时遵循不同的目标，本文希望通过制定一个利益分配机制使得DNO和DGO之间的利益得到协调，引导DGO在进行投资决策时考虑DNO的利益，从而实现帕累托最优。本文的目标函数为

max min{ξ1,ξ2}

(1)

其中，

ξ1=(1-α)×pDNO

(2)

ξ2=(pDGO-cNGO)+α×pDNO

(3)

式中：ξ1和ξ2分别表示DNO和DGO的利润；α表示DNO对DGO的利润分配比例；pDNO表示由于DG的存在给DNO带来的利润；pDGO和cDGO分别表示DGO的收益和成本。

(4)

其中，DNO的成本CDNO主要包括：线损成本CL、线路投资及运维成本CF、变电站投资及运维成本CS以及所购电能的排放成本CE。在本文中，假设所有的投资都在年初进行，则CDNO可以表达为

(5)

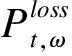
本文所考虑的情景皆为DG正常运行环境下的，DGO的成本CDGO包括运维成本CO和投资成本CI，暂不考虑故障成本。具体表达式为

(6)

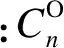
DGO的收益来源于售电收入，电能的价格类型取决于DGO在市场中的角色，可以是双边合约电价，也可以市场电价。本文DGO的电价采用市场价格，其收益pDGO可以表达为

(7)

1.2 约束条件

1.2.1 常规约束

为了保证系统运行的安全稳定性，在构建利益分配机制过程中必须考虑电网运行常规约束条件，主要包括：功率平衡约束、电压约束、分布式发电出力约束、线路及变电站容量约束。

功率平衡约束表达式为

(8)

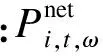
电压约束表达式为

Umin≤Ui,t,ω≤Umax

(9)

式中：Umin和Umax分别表示最低、最高操作电压限制， kV；Ui，t，ω表示在t年，在需求水平ω条件下，母线i的电压等级， kV。

DG出力约束表达式为

(10)

线路和变电站容量约束表达式为

(11)

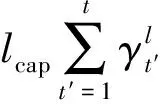
(12)

1.2.2 排放约束

目前，环境问题愈发被重视。本文将环境效益纳入约束条件中，系统排放受到总量限制，如下式所示：

Et≤Elim

(13)

式中：Et表示t年的排放总量，t；Elim为排放限额，t。

总的排放量主要包括2部分：由主干电网产生的排放和由可再生发电机组产生的排放，因此，排放总量Et可以表示为

(14)

1.3 不确定性处理

1.3.1 风电机组发电不确定性处理

风力发电机组的输出功率主要取决于当地的风速，历史风速数据通常由气象部分以h为单位进行记录。一般情况下，风速的变化被看作是一个随机变量，可以使用威布尔分布表示为

(15)

式中vk表示k地区的风速，m/s；ak和bk分别表示形状指数和规模指数，其计算方法为

(16)

式中μk和σk分别表示k地区在特定时间段内的风速均值和标准差[13]。

根据已知的风速分布函数，风力发电机组的输出功率根据风机的技术特性可由下式确定

(17)

1.3.2 市场需求和电价不确定性处理

一般而言，用电负荷和基于市场的电价是具有很大不确定性的。本文为了简化计算，对用电负荷及电价水平进行限定，并通过调整系数反映系统带来的不确定性。

系统中，长期的有功和无功功率需求可以表示为

(18)

在开放市场环境下，购电价格是由竞争决定的，因此在不同的需求水平下电价并不是恒定的。为了不失一般性，假设在不同需求水平下的电价水平为

pω=pγω

(19)

式中p为基本价格，元/( kW·h)；γω表示在需求水平为ω时电价调整系数，并且假定这个调整系数是已知的。

对于长期负荷需求和电价的不确定性，使用公式(11)和(12)进行处理，然而公式中的τω和γω的值仍然是不确定的。本文假设这些不确定值的概率密度函数满足对数正态分布，同时τω和γω概率密度函数的平均值和标准差是确定的，具体确定方法如下所述

(20)

在本文中，使用两点估计法确定概率密度函数的平均值和方差，具体方法如下：

假设有1个函数Y=h(x1,x2,...,xNuv)，该方法是用于解决在已知不确定性变量xi的概率密度函数的条件下，如何求解Y的概率密度函数的问题。实施流程如图1所示。

2 改进的布谷鸟搜索算法

2.1 布谷鸟算法机理及步骤

布谷鸟算法(cuckoo search algorithm)是一种新型的基于全局协同搜索的启发式搜索算法，通过启发函数(任何数学函数)进行搜索，从而找到组合优化问题的优化解[14]。该算法具有概念简单，调整参数少，计算速度快，全局搜索寻优能力强，易于实现等特点。莱维飞行理论主要是指布谷鸟在选巢时其飞行轨迹类似于一种随机行走的形式(random walk)，布谷鸟飞行的距离(步长)满足一个重尾(heavy-tailed)的稳定分布，也就是说布谷鸟的短距离探索飞行与偶尔的较长距离的飞行是相间的。在智能优化算法中采用莱维飞行能扩大种群的搜索范围、增加方案的多样性，更容易得到局部最优解[15-16]。

为了明确算法的适用性并提高其搜索的准确性，布谷鸟搜索算法提出了以下3点假设：

(1)每只布谷鸟每次只产1个卵，并且随机选择寄生巢放置，布谷鸟的卵表示新的方案，巢里原有的卵表示旧的方案；

(2)一部分鸟巢里面已经放置着“优质蛋”，即好的方案，这些鸟巢是不可被利用的，不能被布谷鸟的卵(新的方案)替换；

(3)可被利用来寄生孵蛋的鸟巢的数量G是固定的，并且被寄生的鸟巢的主人发现一个外来鸟蛋的概率为Pa，也就是说能够实现的方案的个数为G·(1-Pa)。

图1 两点估计法实施流程图

基于以上假设，杜鹃鸟寻巢的搜索路径和位置变换的表达式为

(21)

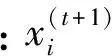
莱维飞行的随机搜索路径满足如下分布：

Levy～u=t-λ,1<λ≤3

(22)

2.2 改进的布谷鸟搜索算法

在基本的布谷鸟搜索算法中，搜索的步长具有随机性，并且缺乏自适应性，无法保证全局的快速收敛。此外，当布谷鸟搜索的鸟巢之间的差异较小，且数量过大时，会造成方案的多样性减少，导致放置鸟卵的巢的位置不再变化(“最佳方案”不再变更)，使算法陷入局部极值中。为解决全局寻优能力和精度间的关系，本文向搜索范围中引入“扰动”以摆脱局部最优。

该方法的基本思路是：设G为布谷鸟的搜索空间，X∈G为任一布谷鸟，X′=C(X)为布谷鸟飞行后所处的新位置，Δ=J(X)-J(X′)表示布谷鸟所处的新位置和原位置的差值，δ∈[-r，r]为随机扰动。扰动执行的方法是：如果Δ′=Δ+δ>0，则保留新位置淘汰旧位置，如果Δ′<0，则淘汰新位置而保留旧位置。如果Δ′=0，则重新扰动。通过“扰动”的方式，以一定的概率接受性能增益不大的借巢行为，淘汰性能增益过小的借巢行为，接受性能增益明显的借巢，从而避免算法陷入局部极优。

该算法的基本步骤为：

(1)设定目标函数为f(Y)，Y=[Y1，…，Yd]T，初始化群体，随机产生n个鸟巢的初始位置Yi(i= 1，2，…，n)，根据模型设置算法参数。

(2)计算每个鸟巢的目标函数值，并记录当前的最优解。

(3)保留上代最优的鸟巢位置，并按位置更新式(21)，对其他鸟巢的位置进行更新。

(4)用随机数R作为鸟巢主人发现外来鸟蛋的可能性与Pa进行比较，若R>Pa，则随机改变鸟巢位置，得到1组新的鸟巢位置。

(5)增加扰动，计算其他鸟巢与最优鸟巢的距离，当其距离满足Δ′=Δ+δ>0时，则保留布谷鸟所处的新位置。

(6)如果没有满足结束条件，则返回(2)。

(7)输出全局最优的鸟巢位置。

3 算例分析

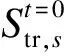
图2 IEEE33节点配电系统接线图

表2 风机技术特性

m/s

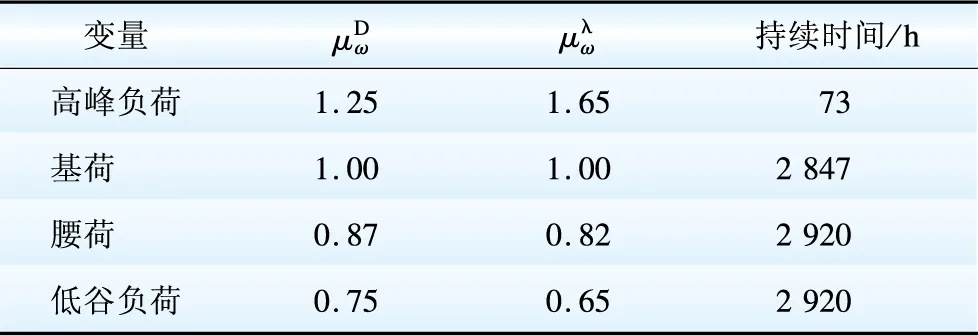
表3 负荷需求、电价调整系数及持续时间预测结果

为了验证本文所建立模型的有效性，我们考虑无利润分配和有利润分配2种情形。

情景1:不存在利润分配

首先分析无利润分配的情形。在本小节中，假设系统中由于DG存在而产生的利润都由DNO获取，

表4 研究中所需使用的其他数据

Table 4 Other used data

即假定α=0%。在该情形中，帕累托最优前沿有20个非劣解，如图4所示。该图说明在没有利益分配的情况下，在13种解决方案中DGO的投资对自己而言是无利可图的。在各帕累托最优方案下，目标函数的值如图3所示。解决方案1的计划安排如表5所示。

在该方案中，DNO与DGO的净利润均为正值，并且使用了3种DG，即风力发电机组、燃气机组和热电联产机组。表5同时给出了母线的安装及投资时间。在该方案中，进行了输电线路的加固，没有变电站的投资。

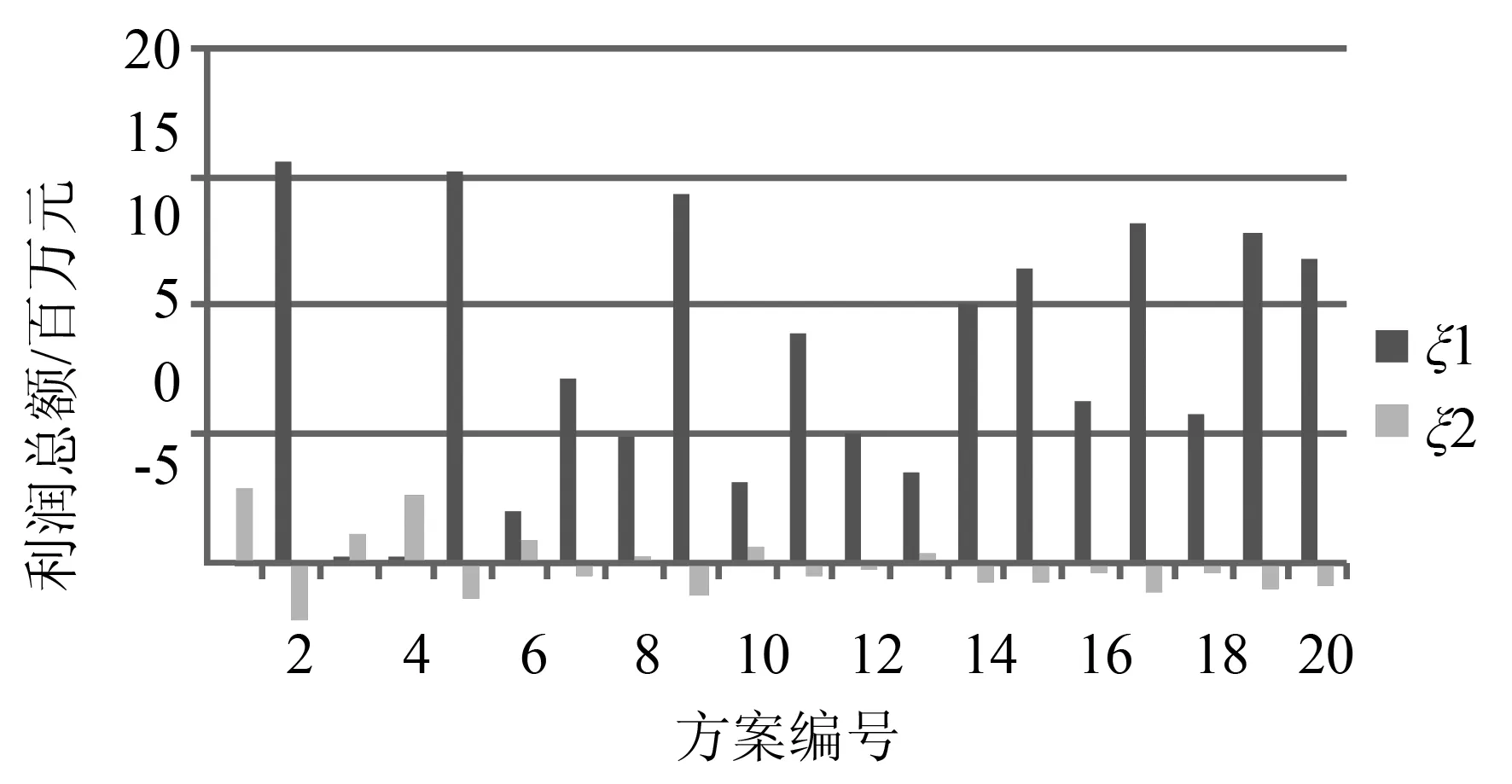
图3 α=0情形下各方案帕累托最优时的目标函数值

情景2：存在利润分配

在本情形中，假设DNO在考虑自身效益的同时，为鼓励DGO投资对DGO进行一定比例的利润分配，即α≠0，但不确定。分析结果如图4和表6、7所示。

图4 α≠0情形下各方案帕累托最优时的目标函数值

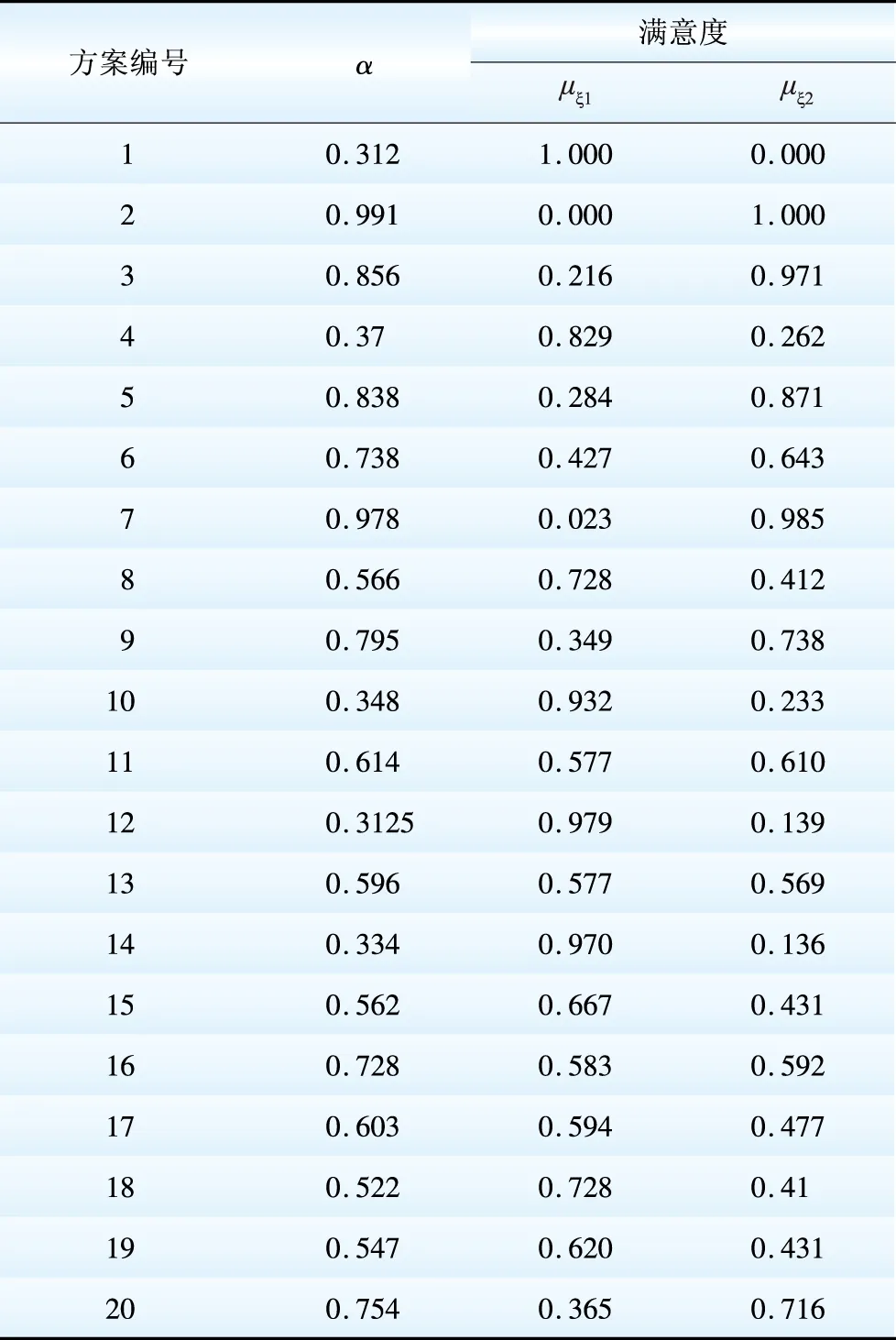
表7 情景2中方案16的计划安排

在此情景中，DNO对DGO的利润分配比例α由优化过程确定。所获得的帕累托前沿有20个非劣解，在所有解决方案中，目标函数值均为正值，这也就意味着在任一方案下DNO和分布式发电上均有利可图。不同方案的区别在于利润数额的不同，因此在方案的比选过程中DNO与DGO会有不同的倾向。利润分配比例的变化幅度很大，最小为31.2%，最大为99.1%。仿真结果如图4所示，图4给出了各方案下DNO和DGO的利润。利润分配比例α以及各利益主体利润最大化的满意程度如表6所示。在选取最终方案时，选取对于2个目标函数来说最小满意度最大时的方案为最优方案，即方案16。在该方案中使用了风电机组、燃气机组、柴油机组和热电联供机组四种DG。母线的安装及投资时间如表7所示。在该方案中同时存在线路加固和变电站加固。

4 结 论

本文提出了用于解决分布式发电和配电网规划的多目标动态模型，并使用改进的布谷鸟搜索算法求解所建模型。文中使用的两步算法，首先寻找能够同时使得DNO和DGO利润最大化的非劣解，然后再从候选集中选取最佳规划方案。文章的最后将所建模型应用于实际的配电网络中，通过对比分析验证了所建模型的灵活性和有效性。本文的目的并不是制定强制交易规则，而是为双方提出了交易新思路，从而达到双赢目的，同时能够有效的满足技术、经济和环境约束。本文所提出的方法可以使得DNO更加有效的鼓励各种分布式发电技术的投资和规划，同时也考虑到了未来各种参数的不确定性，可以帮助规划者更加准确的制定规划。

[1]季阳，艾芊，解大.分布式发电技术与智能电网技术的协同发展趋势[J].电网技术，2010，34 (12)：16-23.Ji Yang，Ai Qian，Xie Da.Research on co-developmental trend of distributed generation and smart grid[J].Power System Technology，2010，34 (12)：16-23.

[2]王成山，李鹏.分布式发电、微网与智能配电网的发展与挑战[J].电力系统自动化,2010,34(2):10-14.Wang Chengshan， Li Peng.Development and challenges of distributed generation， the micro-grid and smart distribution system[J].Automation of Electric Power Systems,2010,34(2):10-14.

[3]Gardner J， Carr-Cornish S G，Ashworth P N.Exploring the acceptance of a domestic distributed energy market in Australia[J].Australasian Journal of Environmental Management，2008，15(2)：93-103.

[4]雷金勇,李战鹰,卢泽汉,等.分布式发电技术及其对电力系统影响研究综述[J].南方电网技术,2011,5(4):46-50.Lei Jinyong,Li Zhanying,Lu Zehan,et al.Review on the research of distributed generation technology and its impacts on electric power systems[J].Southern Power System Technology,2011,5(4):46-50.

[5]张惠卿，李燕青，刘朝霞.配电网中基于改进的多种群遗传算法的分布式发电规划[J].电力科学与工程，2010，26 (12)：4-8.Zhang Huiqing，Li Yanqing，Liu Zhaoxia.Distributed generation planning based on a modified multi-population genetic algorithm in distributed networks[J].Electric Power Science and Engineering，2010，26 (12)：4-8.

[6]崔艳龙.带分布式发电的配电网规划研究[D].成都：西南交通大学，2013.Cui Yanlong.Research on distribution nerwork planning including distributed generation[D].Chengdu：Southwest Jiaotong University，2013.

[7]李振文.计及分布式发电与环网柜的配电网规划方法研究[D].重庆：重庆大学，2012.Li Zhenwen.Distribution network planning considering distributed generation and ring main unit[D].Chongqing：Chongqing University，2012.

[8]Koutroumpezis G N， Safigianni A S， Demetzos G S，et al.Investigation of the distributed generation penetration in a medium voltage power distribution network[J].International Journal of Energy Research，2010，34(7)：585-593.

[9]付丽伟，王守相，张永武，等.多类型分布式电源在配电网中的优化配置[J] .电网技术，2012，36(1)：79-84 .Fu Liwei，Wang Shouxiang，Zhang Wuyong，et al.Optimal selection and configuration of multi-types of distributed generators in distribution network[J].Power System Technology，2012，36(1)：79-84 .

[10]Kaur S，Kumbhar G，Sharma J.A MINLP technique for optimal placement of multiple DG units in distribution systems [J].International Journal of Electrical Power and Energy Systems，2014，23(6)：609-617.

[11]Rouhani A，Hosseini S H，Raoofat M.Composite generation and transmission expansion planning considering distributed generation [J].International Journal of Electrical Power and Energy Systems，2014，65(11)：792-805.

[12]张立梅，唐巍，王少林，等.综合考虑配电公司及独立发电商利益的分布式电源规划[J].电力系统自动化，2011，35(4)：23-28.Zhang Limei，Tang Wei，Wang Shaolin，et al.Distributed generators planning considering benefits for distribution power company and independent power suppliers[J].Automation of Electric Power Systems，2011，35(4)：23-28.

[13]Zeng Bo，Zhang Jianhua，Ouyang Shaojie，et al.Two-stage combinatory planning method for efficient wind power integration in smart distribution systems considering uncertainties [J].Electric Power Components & Systems，2014， 42(15):1660-1672.

[14]候慧超.布谷鸟优化算法改进及与粒子群算法融合研究[D].锦州：渤海大学，2014.Hou Huichao.Improving cuckoo algorithm and particle swarm algorithm fusion research[D] .Jinzhou：Bohai University，2014.

[15]李煜，马良.新型元启发式布谷鸟搜索算法[J].系统工程，2012，30 (8)：64-69.Li Yu，Ma Liang.A New metaheuristic cuckoo search algorithm[J].Systems Engineering，2012，30 (8)：64-69.

[16]陈健，陈雪刚，张家录，等.杜鹃鸟搜索算法优化最小二乘支持向量机的网络入侵检测模型[J].微电子学与计算机，2013，30 (10):29-32.Chen Jian，Chen Xuegang，Zhang Jialu，et al.Network intrusion detection model based on least squares support vector machine optimized by modify cuckoo search algorithm [J].Microelectronics & computer，2013，30 (10):29-32.

[17]Baran M E，Wu F F.Network reconfiguration in distribution systems for loss reduction and load balancing[J].IEEE Transaction on Power Delivery，1989，9(4)：101-102.

(编辑：蒋毅恒)

Benefit Equilibrium Model of DGO and DNO in Deregulated Environment Based on ICSA

CHEN Zheng1，ZENG Ming2，ZHANG Xiang1，CHANG Qicheng3， OU Peng1，2，SONG Yihang1，QIAN Qiqi2，OUYANG Shaojie2，LIU Yingxin2

(1.Electric Power Research Institute of China Southern Power Grid，Guangzhou 510080，China; 2.College of Economics and Management, North China Electric Power University，Beijing 102206，China; 3.Beijing University of Posts and Telecommunications，Beijing 100876，China)

In recent years, distributed generation obtains rapid development for its energy-saving and environment protection.However, the network access of distributed energy will cause certain impact on the interests of the distribution network operators (DNO), which may hinder harmonious development of them.This pape reconciled the both interests of DNO and distributed generation owners (DGO), and studied the combined optimization problem of distributed generation investment and distribution network construction planning.The profit distribution coefficient was introduced during the construction of objective function so as to achieve the win-win purpose.Besides, the model needed to satisfy both the security and stability operation of distribution network and the emission reduction targets constraints.And the two-point estimate model was used to determine the uncertainty factors in the model.This paper used improved cuckoo search algorithm (ICSA) to solve the constructed model.At last, a IEEE33 nodes distribution system was used to verify the feasibility and effectiveness of the provided model by cases comparison.

deregulation; benefit equilibrium; distributed generation owner; distribution network operator; improved cuckoo search algorithm

国家自然科学基金项目(71271082)。

TM 715

A

1000-7229(2015)08-0007-08

10.3969/j.issn.1000-7229.2015.08.002

2015-05-26

2015-07-14

陈政(1976)，男，硕士，高级工程师，研究方向为能源经济、电力系统规划；

曾鸣(1957)，男，教授，博士生导师，研究方向为电力市场及技术经济研究；

张翔(1988)，男，硕士，工程师，研究方向为能源经济、电力系统规划；

常启诚(1994)，男，本科，研究方向为数学及应用数学；

欧鹏(1987)，男，硕士研究生，经济师，研究方向为能源经济、电力系统规划；

宋艺航(1986)，男，博士，工程师，从事能源经济、电力风险管理方面的研究工作;

钱琪琪(1992)，女，硕士研究生，研究方向为新能源；

欧阳邵杰(1989)，男，博士研究生，研究方向为主动配电网方面；

刘英新(1993)，男，硕士研究生，研究方向为分布式发电、配电网规划。

Project Supported by National Natural Science Foundation of China(NSFC)(71271082).