全轮廓拟合悬滴法表面张力实验系统

艾芳洋，毕胜山，吴江涛

(西安交通大学 热流科学与工程教育部重点实验室，陕西 西安 710049)

全轮廓拟合悬滴法表面张力实验系统

艾芳洋，毕胜山，吴江涛

(西安交通大学 热流科学与工程教育部重点实验室，陕西 西安 710049)

摘要：研制了悬滴法表面张力实验系统，温度测量范围为283.15~323.15 K，温度测量误差不超过±0.5 K. 采用轮廓拟合法对表面张力进行计算，在VC++环境下分别用坐标轮换法和Nelder-Mead单纯形法进行了编程实现. 利用正庚烷和乙醇对实验系统进行校验,结果表明：2种物质的表面张力实验值与文献值偏差在±0.2 mN·m-1以内，坐标轮换法和Nelder-Mead单纯形法的计算结果一致.

关键词：悬滴法；轮廓拟合；表面张力

1引言

表面张力是流体的重要热物理性质之一，也是描述表面现象的最主要的物理量. 由于表面现象在石油化工、能源动力及生命科学等领域的广泛存在，准确的表面张力数据已经成为在这些领域开展研究工作必不可少的基础数据. 在表面张力的诸多实验测量方法中，悬滴法具有测量精度高、浸润性要求低、样品用量少、适用温度及压力范围大等诸多优点.

悬滴法测量表面张力的理论基础是Young-Laplace方程[1-2]，它描述了被界面分开的2种均质流体所处的静力平衡关系. 1883年，Bashforth和Adams推导出了处于表面张力和重力平衡时的悬滴轮廓外形的理论方程[3]. 基于此方程，Andreas于1938年提出了选择平面法[4]，这一方法通过选择悬滴的特征平面来定义形状因子，并通过查表的方法得到相关参量，最终计算出表面张力. 选择平面法只需要2个特征平面的尺寸，操作简单，但精度较差. 随着数字计算技术的发展，全轮廓拟合悬滴法得到快速发展. 1969年，Maze和Burnet[5]开发了用于计算座滴的表面张力和接触角的数值算法，并通过定义目标函数进行参量的寻优，这一处理思路被广泛借鉴. 1983年，Rotenberg等[6]提出了轴对称液滴形状分析法(ADSA)，对图像处理方法及优化算法都进行了改进，使用C语言编写的计算程序具有良好的操作性和可移植性，使得该方法的应用成果十分丰富. 此外，悬滴法的处理方法还有基于有限元分析的γ-PD-FEM算法[7]以及Song和Springer[8]、Thiessen[9]等人提出的算法. 国内有关悬滴法表面张力测量的研究与国际水平有着一定的差距，且主要集中在对商业悬滴法表面张力设备的应用上. 高树棠等[10]利用微悬滴法测定了某些体系的低界面张力，吴爱民等[11]利用悬滴法对高分子熔体界面张力进行了测量，宋瑛等[12]利用悬滴法对8个二元液液系统的表面张力进行了研究，讨论了界面张力与温度之间的关系.

本文在对悬滴法表面张力实验原理进行研究的基础上，在C++语言平台，开发了全轮廓拟合法表面张力算法程序，研制了悬滴法表面张力实验系统，对实验系统进行了检验和误差分析.

2实验原理

经典的Young-Laplace方程给出了被一界面分开的2种均质流体所处的静力平衡关系，即

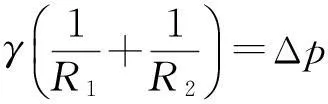
(1)

在表面张力和重力作用下，液滴成拉伸状态，如图1所示. 对悬滴轮廓线上任意一点，由曲率半径几何和静力平衡关系，推导得到Bashforth-Adams方程：

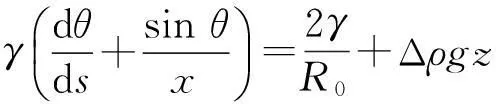
(2)

其中，x和z分别为横纵坐标，s为弧长，Δρ为悬滴界面密度差，θ为悬滴表面某点切线与X轴的夹角，R0为悬滴端点处的曲率半径，g为重力加速度.

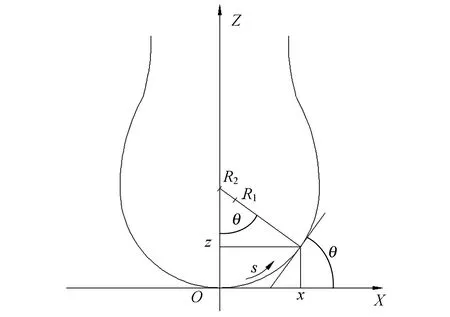
图1　悬滴外形几何示意图

用R0对x，z和θ进行无量纲化，即

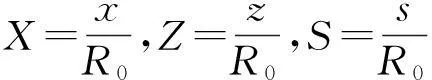
(3)

代入式(2)，可得：

(4)

其中β为定义的悬滴形状因子，表示为

(5)

由图1又可以得到几何关系：

(6)

式(4)和式(6)组成了关于轮廓点无量纲坐标的方程组，对于给定的R0和β，求解方程组，可以得出悬滴的理论曲线. 对式(5)变形可以得到表面张力γ的计算式：

总之，在网络技术的驱动下，实现倒逼新闻传播教育的转型与创新，无论从培养目标的设定，还是从教学体系的构成和具体教学内容的设计上，抑或是在实践教学条件的建设和教学方法的更新上，都需要摒弃老观念老方法，要有“壮士断腕”的气概，才能让我们的教育不负时代，不负使命。

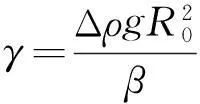
(7)

式中，Δρ和g视为已知参量，R0和β通过全轮廓拟合获得，从而获得表面张力.

3全轮廓拟合法

对于式(4)和式(6)组成的方程组，目前并没有方法可以求得其解析解，本文采用四阶Runge-Kutta法进行数值求解，所得数值解即为悬滴的理论轮廓曲线[13]. 另一方面，将实验所得的悬滴图像进行图像处理，提取边缘之后便得到悬滴的实际轮廓曲线. 悬滴理论轮廓曲线与实际轮廓曲线不是完全重合的，将二者的差值定义为目标函数，对此目标函数进行优化求出最优的R0和β参量值，代入式(7)中便可求得表面张力值. 目标函数的定义是选用悬滴全轮廓上的数据点，区别于选择平面法选取某几个特殊点的处理方法，因而本文的处理方法称为全轮廓拟合法，其处理流程如图2所示，下面将分步骤介绍.

3.1　图像处理

获得悬滴图像之后需要通过图像处理来获取实际轮廓曲线. 图像处理过程分为：平滑滤波、边缘检测、边缘锐化以及坐标提取与变换. 其中，平滑滤波用于去除噪点；边缘检测使用Canny算子[14]，Canny算子能够很好地兼顾抑制噪声和边缘的精确定位；边缘锐化使得边缘更加规整、清晰. 如图3所示.

由于所得到的边缘图像是数字图像，数字图像的处理是从图像的左上角开始，并逐行逐像素进行，也就是说数字图像的坐标原点位于图像的左上角. 要便于下一步的目标函数构造及拟合计算，必须得到以液滴端点为坐标原点并按逆时针次序排列的轮廓坐标，于是便需要进行轮廓坐标的排序与变换. 此外，所得数字图像的坐标值为像素坐标(pixel)，必须通过设定以中间标尺来进行坐标尺度变换，将像素坐标变换为实际尺寸坐标(mm). 最后，将经过以上处理所得的实际轮廓坐标存储在预先定义好的数组中. 轮廓坐标的排序与变换过程如图4所示.

3.2　目标函数构造

通过解方程组得到悬滴的理论轮廓曲线u(xi，zi)，通过图像处理得到了悬滴的实际轮廓U(Xi，Zi)，如图5所示，u(s)与U(s)并不重合. 定义ei为单个点的误差函数：

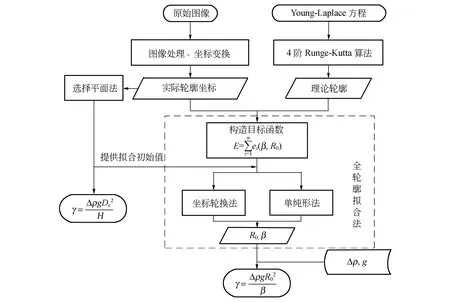
图2　悬滴法的处理流程

(a)原图　　　　　　　(b)平滑滤波图

(c)边缘检测图　　　　(d)边缘锐化图图3　悬滴的边缘检测

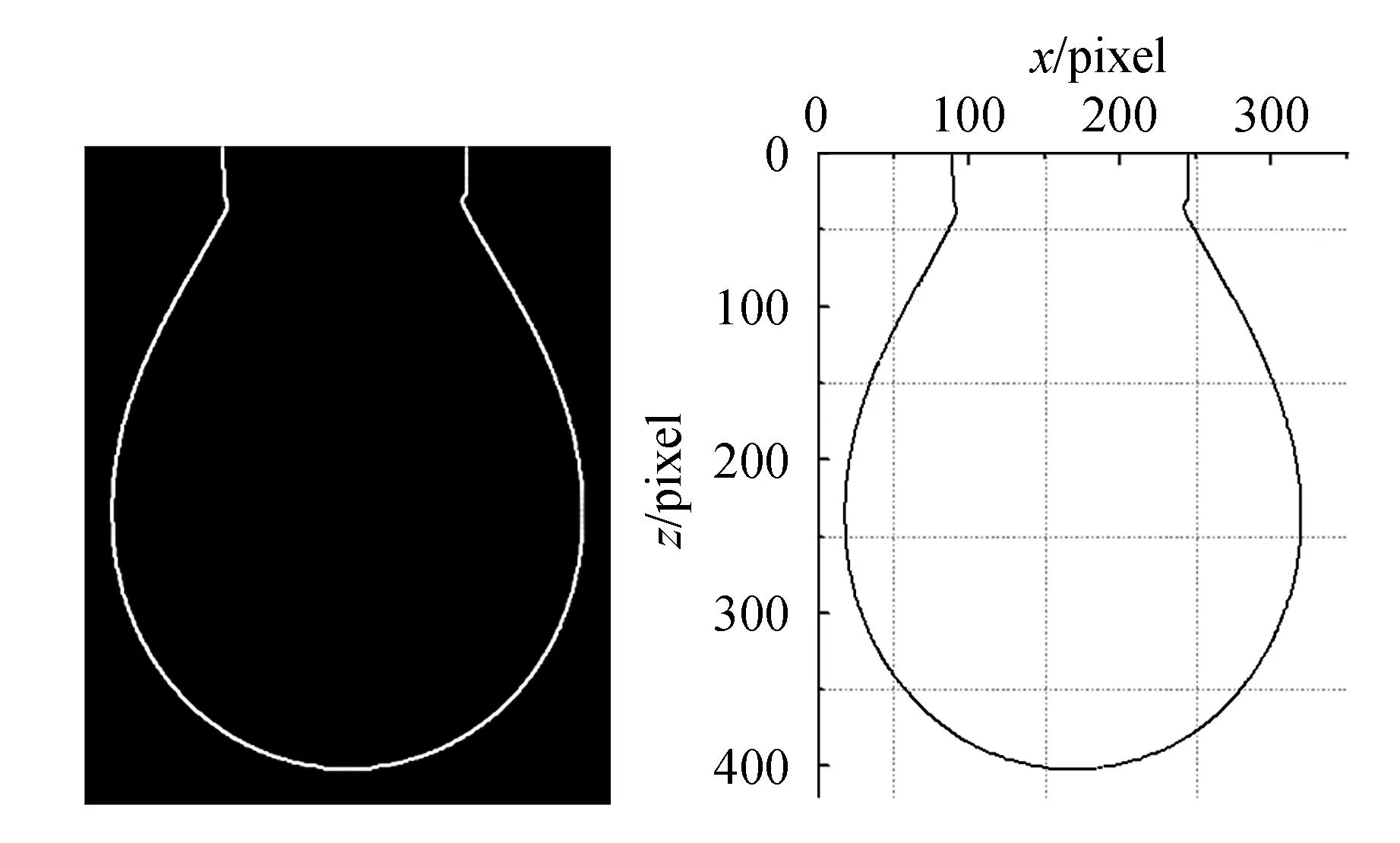
(a)　　　　　　　　　　(b)

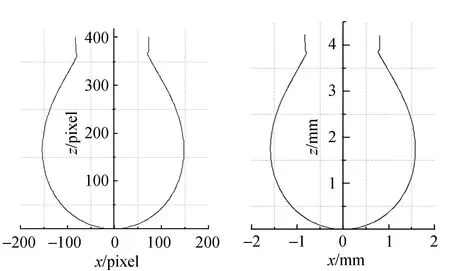
(c)　　　　　　　　　　(d)图4　轮廓坐标的排序与变换

图5　理论曲线与实验点的关系

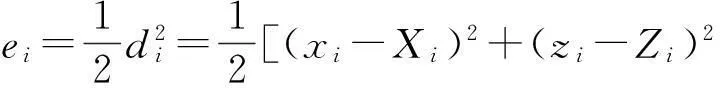
(8)

于是，全轮廓的误差函数为

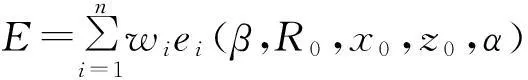
(9)

其中，wi为权重因子，一般设定为1. E是关于形状因子β、端点曲率半径R0、端点坐标(x0,z0)及图像偏转角α的函数. 以E为目标函数进行的优化是5参量优化，且由于包含轮廓的全部坐标点，计算量较大. 本文通过对端点坐标进行准确定位，能够在优化计算之前将(x0,z0)设为常量，通过设置铅垂线进行角度校准，将偏转角α设为0°，因而本文的目标函数是关于β和R0的函数，即

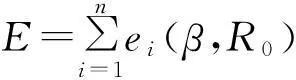
(10)

由于悬滴轮廓的对称性，一般选取右半轮廓上的点进行目标函数的构造，这一处理不会影响最终的计算结果，且能将计算效率提高1倍以上.

3.3　优化算法

目标函数的优化问题是多维无约束最优化问题，解决这一类问题的方法主要有直接法和间接法2类. 直接法直接用函数值来确定搜索方向；间接法需要通过计算函数的一阶或二阶导数值来确定搜索方向. 直接法不需要对导数和Hessian矩阵进行求解，因而具有更强的适应性，但是维数较高时其收敛速度相对较慢. 本文目标函数是二维函数，使用直接法计算是完全适用的. 本文使用坐标轮换法及Nelder-Mead单纯形法来进行优化求解，对2种算法都在VC++环境下进行了编程实现.

3.3.1坐标轮换法

坐标轮换法，就是把对n个变量进行寻优转化为交替轮换地进行单变量寻优. 选择初始点X0作为搜索的起点，依次在各个维度进行搜索，每次都设定1个参量为变量，其他各个参量均为常量. 一轮循环结束后，判断是否满足设定的收敛条件，若满足则输出并结束循环，不满足则以本轮的搜索结果为起点开始下一轮的循环，直至满足收敛条件为止.

3.3.2Nelder-Mead单纯形法

1个单纯形就是1个几何体，在二维情况下的单纯形就是1个三角形[15]. 单纯形法就是通过反射、扩张、收缩和多维收缩这几个基本步骤不断地对初始单纯形进行处理，直至满足设定的收敛条件. 迭代的终止条件是单纯形各个顶点函数值的离差是否小于某一设定的极小值ε，即

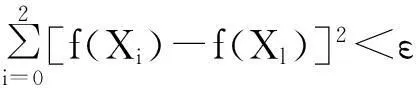
(11)

坐标轮换法与Nelder-Mead单纯形法的参量预估值均由选择平面法计算得到，选择平面法是悬滴法的一种非拟合算法，具体计算过程可参见相关文献[4].

4实验系统

图6所示为悬滴法实验系统的基本组成，包括实验平台、光源、散光片、悬滴形成装置、镜头、相机和计算机等.

图6　悬滴法实验系统

实验平台是整个实验系统的基座，一般由表面平整度高且可准确调节水平度的光学平台充当.

自然光照条件下所拍摄的液滴一般不够清晰，光源与散光片共同为悬滴提供背景光，使得拍摄到的液滴图像与背景具有强烈的对比度，便于之后的图像处理. 光源由艾菲特光电技术有限公司提供，型号为AFT-BL50.

镜头与相机作为整体，用来进行液滴图像的采集. 相机与计算机相连接，计算机上安装有与相机相配的图像采集卡及采集软件. 使用的相机为最大可达1 400万像素的CMOS相机MV-1400UC，由维视数字图像技术有限公司提供.

液滴形成部分的装置包括注射器、平头针、石英比色皿等，这一部分集成在恒温室中. 液滴在不锈钢平头针针口处形成，平头针插入密封的石英比色皿中，而比色皿则置于恒温室的中心. 恒温室由内至外分别是循环液回路、保温材料和外壳，其中循环液回路由导热性能良好的铜管构成，循环液通过导管由外接的恒温槽导入并进行循环以控制整个恒温室的温度. 外循环采用上海衡平仪器仪表厂生产的低温恒温槽进行控温，型号DC-4006，温度波动度±0.05 K. 采用铜-康铜温差电偶作为测温元件，以Agilent 34970A数据采集器作为测温仪器，温度测点布置在最接近悬滴温度的不锈钢针针口处. 实验前，对铜-康铜温差电偶和Agilent 34970A组成测温系统在Fluke 7073型恒温槽中在10~80 ℃温度范围内进行了标定，标定后的温度测量不确定度小于±0.5 K.

5系统校验与误差分析

5.1　系统校验

利用正庚烷和乙醇进行了实验系统的校验，分别用坐标轮换法和单纯形法进行计算. 计算结果如表1所示. 表中的γexp代表实验中各种方法的计算值，γref代表作为参考的实验值，通过NIST REFPROP 9.0[16]获得. 用于计算的密度数据同样来源于NIST REFPROP 9.0.

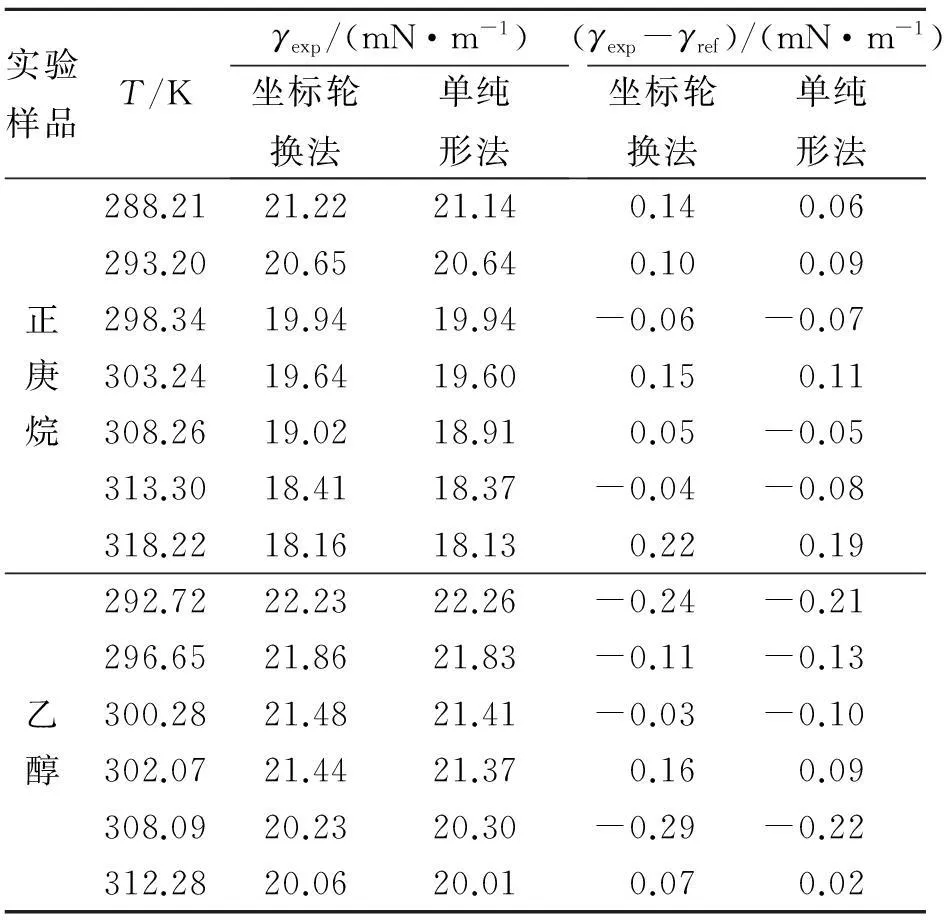
表1　正庚烷及乙醇的实验结果

5.2　误差分析

DC-4006低温恒温槽的温度波动度为±0.05 K，铜-康铜温差电偶与Agilent 34970A数据采集器组成的测温系统的测温不确定度为±0.5 K. 对于一般的待测物质，温度变化1 K所引起的表面张力变化小于0.2 mN·m-1，故因温度测量引起的误差应小于0.11 mN·m-1. 对于本文所测量物质的表面张力范围(γ<50 mN·m-1)，此项的相对误差小于0.3%.

根据表面张力的计算式(7)和误差传递原理[17]可以得到表面张力的相对误差公式：

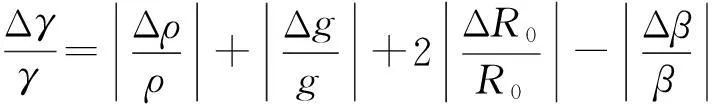
(12)

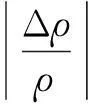
6结论

研究了悬滴法表面张力的测量方法，确定了悬滴法中的平滑滤波-Canny算子边缘检测-边缘锐化的图像处理过程以及边缘坐标提取方法以及目标函数的构造方法. 利用坐标轮换法和单纯形法2种轮廓拟合算法实现了对目标函数的寻优. 正庚烷与乙醇的实验结果显示，2种方法的计算结果具有较好的一致性，单纯形法的计算效率更高. 设计了悬滴法表面张力实验系统，系统的温度测量范围是283.15~323.15 K，温度测量误差不超过±0.5 K. 通过误差分析确定实验系统测量的相对误差小于±1.2%. 用正庚烷和乙醇对实验系统进行了校验，实验结果显示：系统具有较好的稳定性，测量的正庚烷及乙醇表面张力值与文献值偏差均在0.2 mN·m-1以内.

参考文献：

[1]Young T. An essay on the cohesion of fluids [J]. Philosophical Transactions of the Royal Society of London, 1805,95:65-87.

[2]Laplace P S. Traité de mécanique céleste [M]. Paris: Courcier, 1805：1-79.

[3]Bashforth F, Adams J C. An attempt to test the theories of capillary action: by comparing the theoretical and measured forms of drops of fluid [M]. London: Cambridge University Press, 1883.

[4]Andreas J M, Hauser E A, Tucker W B. Boundary tension by pendant drops [J]. Journal of Physical Chemistry, 1938,42(8):1001-1019.

[5]Maze C, Burnet G. A non-linear regression method for calculating surface tension and contact angle from the shape of a sessile drop [J]. Surface Science,1969,13(2):451-470.

[6]Rotenberg Y, Boruvka L, Neumann A W. Determination of surface tension and contact angle from the shapes of axisymmetric fluid interfaces [J]. Journal of Colloid and Interface Science, 1983,93(1):169-183.

[7]Dingle N M, Tjiptowidjojo K, Basaran O A, et al. A finite element based algorithm for determining interfacial tension (γ) from pendant drop profiles [J]. Journal of Colloid and Interface Science, 2005,286(2):647-660.

[8]Song B, Springer J. Determination of interfacial tension from the profile of a pendant drop using computer-aided image processing: 1. Theoretical [J]. Journal of Colloid and Interface Science, 1996,184(1):64-76.

[9]Thiessen D B, Chione D J, Mccreary C B, et al. Robust digital image analysis of pendant drop shapes [J]. Journal of Colloid and Interface Science, 1996,177(2):658-665.

[10]高树棠,张启桓. 应用微悬滴法测定低界面张力[J]. 化学通报,1983(6):25-31.

[11]吴爱民，孙载坚. 悬滴法高分子熔体界面张力测量仪[J]. 中国塑料,1994(2):47-52.

[12]宋瑛，田宜灵，肖衍繁，等. 二元液液系统界面张力[J]. 化工学报,1999(5):620-628.

[13]Neumann A W. Applied surface thermodynamics [M]. New York: CRC Press, 2010.

[14]Canny J. A computational approach to edge detection [J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 1986(6): 679-698.

[15]普雷斯，胡健伟. C++ 数值算法[M]. 北京:电子工业出版社,2005.

[16]Lemmon E W, Huber M L, McLinden M O. REFPROP 9.0[CP].Boulder, Colorado: NIST, 2010.

[17]杨旭武. 实验误差原理与数据处理[M]. 北京:科学出版社,2009.

[责任编辑：任德香]

Surface tension experiment system with full-profile fitting pendent drop method

AI Fang-yang, BI Sheng-shan, WU Jiang-tao

(Key Laboratory of Thermal Fluid Science and Engineering of Ministry of Education, Xi’an Jiaotong University, Xi’an 710049, China)

Abstract:A surface tension experiment system using full-profile fitting pendent drop method was built. The system could work at temperatures ranging from 283.15 to 323.15 K and its uncertainty of temperature measurement was better than ±0.5 K. The full-profile fitting was implemented with coordinate alternation method and Nelder-Mead simplex method with VC++. The surface tensions of n-heptane and ethanol were measured with this system. The deviations between experimental data and literature data were less than 0.2 mN·m-1, which proved the reliability and stability of the system. Besides, the analysis of experimental data suggested that both coordinate alternation method and Nelder-Mead simplex method had good convergence and the latter was more computationally efficient.

Key words:pendent drop method; full-profile fitting; surface tension

中图分类号：O552.421

文献标识码：A

文章编号：1005-4642(2015)05-0001-06

作者简介：艾芳洋(1989-)，男，湖北崇阳人，西安交通大学能源与动力工程学院硕士研究生,研究方向为表面张力.通讯联系人：毕胜山(1978-)，男，辽宁兴城人，西安交通大学能源与动力工程学院副教授，博士，主要从事热力学及流体热物性研究.

基金项目：国家自然科学基金(No.51276142)；中央高校基本科研业务费专项资金(No.08143036)

收稿日期：2014-09-16；修改日期：2015-03-20