一种高分辨率遥感影像多元线性回归建模方法

孟小亮，粟骏龙，王帅，杨潇

(武汉大学国际软件学院，武汉 430079)

一种高分辨率遥感影像多元线性回归建模方法

孟小亮，粟骏龙，王帅，杨潇

(武汉大学国际软件学院，武汉 430079)

针对高分辨率遥感影像数据量大、计算难度大的特点，该文采用等宽规则划分、分步读取和统一计算的方案，提出高分辨率遥感影像多元线性回归模型建立算法，确保遥感影像的每个像素点都参与模型的建立。并根据建模算法，设计与开发基于Web服务的多元线性回归在线分析软件。经实验，由改进后算法建立的回归模型生成的预测影像更精确，算法能够成功运用于高空间分辨率遥感影像。本模型算法及软件可应用和推广于去云和去噪等遥感影像处理。

遥感；高空间分辨率；多元线性回归；模型；规则划分

0 引 言

近年来国内外对高分辨率遥感影像的多元线性回归模型的研究增多。多元线性回归模型预测法是数据挖掘中的一个重要内容，在遥感影像分析中，多元线性回归对遥感影像的去云、去噪以及图像校正等多个方面都有着效果良好的运用[1]。去云处理利用多时相遥感影像进行镶嵌，获得无云影像并采用辐射归一化等线性回归模型方法改正不同时相影像的辐射差异，实现云检测和去除[2]。去噪处理则是利用谱间相关性，通过多元线性回归变换得到预测图像和残差图像，进行综合去噪处理[3]。多元线性回归模型的另一重要运用是影像预测[4]，即利用多元线性模型，对单幅或者多幅影像建立其回归模型，根据模型的参数，生成预测图像[5]。

高分辨率遥感影像因其具有数据量大与计算复杂的特征，对其建立多元线性回归模型需进行大量运算。考虑到计算机的内存以及运算能力限制，一般只取其中一定数量的像素点进行分析，得到的线性回归模型精度不能得到保障。本文主要对高分辨率遥感影像多元线性回归模型的建立进行研究与实现，采用分块处理与统一计算的方案，实现建立所有像素点参与即无限数据量的多元线性回归模型，进行建模算法改进，提高处理效率，并实现基于Web服务的在线回归分析软件。

1 多元线性回归模型

线性回归是用回归分析确定两种及以上变量间相互依赖的定量关系的一种统计分析方法[6]。多元线性回归模型主要表现在有多个自变量参与运算[7]，在实际应用中采用的多元线性回归模型，待分析波段具有两到多个，对波段进行回归分析，建立回归方程，挖掘出其中的关联模式。

随机变量即波段y与一般变量波段x1,x2,x3,…,xp的线性回归模型的一般形式为[8]：

y=β0+β1x1+β2x2+…+βpxp+ε
i=1,2,…,p

(1)

其中，p为自变量数目，βj称为回归参数。模型中自变量的数目为(p+1)，ε是随机误差，对随机误差项通常假定：

(2)

称E(y)=β0+β1x1+β2x2+…+βpxp为理论方程。对于一个实际问题，如果掌握n组观测数据(xi1,xi2,xi3,xi4,…,xip,yi)，则该高分辨率遥感影像数据的线性回归模型可表示为：

(3)

写成矩阵形式为：

y=Xβ+ε

(4)

建立多元线性回归模型，即求解此方程系数、复相关系数，以及偏回归系数的过程。

1.1 遥感影像多元线性回归分析步骤

针对高分辨率遥感影像数据量大的特点，应确保模型能够将待处理遥感影像的所有像素点都纳入回归模型的建立中。具体步骤为：

①选取统一地域、同一分辨率的多幅待处理的遥感影像。

②选择所感兴趣遥感影像的某一波段的像素值作为因变量，其他遥感影像的一个或多个波段的像素值作为自变量。

③调用GDAL库分块读取遥感影像，根据改进后的多元线性回归模型算法求出多元线性回归模型，和该回归模型的偏差平方和、平均标准偏差、复相关系数，及每个自变量的偏相关系数。

④根据偏相关系数以及复相关系数等数据，确定该模型的可靠度，如某项自变量的偏相关系数过低，可以剔除该自变量继续构建回归模型，根据新回归模型的复相关系数来判断是否新模型比旧模型更加拟合。

⑤重复步骤③和④，直到新回归模型的复相关性达到令人满意的程度(系数>0.6)。

1.2 高分辨率遥感影像的分块处理

高分辨率遥感影像每幅文件大小一般在1G以上，有些分辨率高、跨地域广的甚至达到2G或者以上[8]。在进行回归分析的时候，需要的是对两幅至多幅遥感影像进行同时建模与分析，在实际应用中，我们一般需要对所有的同地区的多个影像进行多元回归建模[9]，数量会在2到7个之间。当遥感影像数据过大时，同时处理的存储需求会超过当今服务器的普遍内存大小(8G)。为能够有效地同时对所有影像的像素点进行多元线性回归建模，需要对遥感影像进行分步加载处理。

本研究采用宽等分划分原则，按照相同比例划分影像，当待分析的影像比较大的时候，可以适当调整切割比例。采用GDAL库对遥感影像的像素值进行读取，以矩形划分遥感影像能够很好地支持GDAL库的读取载入工作。以宽等划分原则进行区域划分读取到的像素值数组，能够方便地取到划分区域边缘部分的像素值，提高算法运行效率。当影像文件的长远大于宽，如使用等宽划分原则，可能会占满内存，这时采用以长等分的分块方案。

1.3 基础模型设计与实现

根据数学研究，建立多元线性回归模型即为求解y=Xβ+ε与相关参数的过程。由多元线性回归模型的求解过程中可知，建立多元线性回归模型的主要步骤即求解矩阵β[10]。在模型的建立过程中，并不能够将数据分开进行求解，即不能够将每一个数据作为一个独立的个体来运算，而必须要把数据结合起来进行运算，这就要求建立多元线性回归模型时必须一步完成，而不能依据一部分数据先建立初步模型，再补充数据加以求解。所以，在建立模型的过程中，必须要实时地统计每个在运行中需要计算的量。但是在数据量非常大的时候，为了防止内存溢出，输入时并不能够全部同时进行输入，所以在实现算法时，需要采用数据注入方案，即在计算过程中，每当需要用到数据的时候，即从注定的地点中加载读取一部分数据，得到需要的一部分统计值，然后再根据算法需求把前面得到的结果与第二次注入加载的数据进行运算，直到统计完所有的数据，再进行下一步的操作[11]。最后，得到所有的统计数据，并解出该矩阵。根据多元线性回归模型的数学实现，需要经过遍历数据进行计算的主要统计数据为[12]：

(5)

其中，m为自变量即参与运的个数，n为遥感图像的像素个数。

(6)

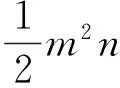
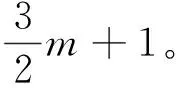
2 建模算法改进

为提高多元线性回归分析的精确度，确保每个参与模型计算的像素点的有效性，需要对参与模型的像素点进行一定的处理，对多元线性回归建模算法进行改进，改进后的建模算法如图2所示，改进方法如下：

图1 多元线性回归建模算法流程

图2 改进后的多元线性回归建模算法流程

(1)排除干扰像素：在一些未经过处理过的遥感影像中，在用户所感兴趣的图像周围有大片空白，如果对这些空白区域的像素值也进行一并处理的话，建立的回归模型的可信度会大大降低。所以在对这些影像建立回归模型的时候，必须进行干扰像素点的排除。即在每次进行分块输入的时候，对每个点的像素值进行一次判断，如果该像素值为0或者null，对该点进行排除，不计入模型建立的计算中，同时，排除其他对应自变量与因变量影像中的点。使用此算法会增大算法的运行时间，最佳情况下，对一幅图像的所有像素点进行一次判断即可，但是，当图像过大需要进行分块加载的时候，对每一块区域可能需要进行重复的判断。为了提高效率，在对每一块区域的像素值进行处理的时候，需要判断该区域是否为干扰区域。

(2)排除干扰区域：根据遥感图像的连续性特征，在对干扰区域进行排除的时候，只需要取该区域最外层的像素点进行判断即可。当以宽等分进行区域划分的时候，只需取第一行与最后一行的像素值。因为以GDAL库读取像素值的时候，矩形区域内的像素值是以数组方式进行读取的，所以在宽等分进行区域划分的情况下，只需取数组前后各一段区域的值进行判断即可。

(3)遥感影像筛选：判断影像是否具有空白区域，筛选算法与排除干扰区域的算法相似。

(4)指定区域进行多元线性回归分析：用户并不需要对全影像进行分析，只需对某地块建立回归模型。截取区域进行分析能有效地避免进行干扰像素与干扰区域的排除步骤。采用以多边形区域进行截取的方案，即用户先在原图像上记录下需要截取的区域的多边形的点的坐标，在算法运行时只对在多边形内的像素点进行处理。判断点在多边形内的算法采用射线算法。使用这种改进后的算法能够对指定区域进行回归分析，提升模型的可靠性。但是需要对原图像进行一些前期的处理，并且需要花费内存来记录每个点的坐标值。在对一些干扰区域较多并且地貌变化较大的影像运用这种算法较好。

表1为改进前后建模算法在服务器上的平均运行时间比较，都采用等宽划分原则。运行的服务器CPU为Xeon E5606 2.13GHz，内存为4G。改进后算法的运行时间与原算法运行时间相比只是小量幅度提高，但改进后的算法能够通用于大多数高分辨率遥感影像。改进后算法因对干扰像素进行了排除，所以能有效地提高算法准确性。

3 实 验

3.1 建模算法软件开发

实验通过在线分析软件实现操作。本研究基于改进后建模算法和Web服务开发了高分辨率遥感影像多元线性回归的在线分析软件。基于SOA和Web服务，可实现与其它各类平台的动态组装和服务集成，从而解决实现模型的在线服务。用户通过3个步骤实现在线分析：

①选择数据并进行解析。

②根据解析的数据信息选择系统处理范围与分块处理次数。

③选择分析处理的波段进行多元线性回归分析并生成回归分析结果的XML数据用于实现Web服务的数据交换。XML数据内容包括回归方程、偏回归系数、复相关系数、残差平方和、回归离差平方和与平均标准偏差。

表1 改进前后多元线性回归建模算法运行时间比较

3.2 算法实验

实验选取内蒙古克什克腾旗的3幅高分辨率不同波段的Landsat影像。如图3所示，图3(a)与图3(b)遥感影像作为自变量x1，x2，图3(c)为因变量y。 通过改进后的建模算法得到回归方程：

y=0.2867940258808611x1+
0.38861042523149747x2-11.532858616775059

(7)

其中，x1与x2的偏回归系数分别为：0.9863878945797896，0.9761805879125711，复相关系数为：0.8970760979716704。

由回归方程与回归参数可看出，自变量与因变量之间关联紧密，回归模型拟合良好，以y的像素值生成新影像，即图3(d)。对比图3(c)与图3(d)可以看出基本吻合，回归模型建立成功。

然后按照随机取点的方法建立回归模型，在整个影像的全图范围中随机选取1000个像素点，建立回归模型，根据像素点计算得到回归方程：

y=0.49594377162346516x1+
0.19592178569106094x2-13.8567974531521

(8)

其中，x1与x2的偏回归系数分别为0.9990670704097192，0.9729046924696167，复相关系数为0.7773960325549288。

根据传统建模算法生成的新影像图与原影像图进行像素相减取绝对值生成的残差影像，与改进后算法得到的模型的残差影像进行对比，结果显示改进后模型的残差影更加接近于全黑，即接近于全零像素。通过计算可知，改进后模型与原影像的像素值平均相差4.4，而随机选取1000个像素点进行测试的像素值平均相差为14.5。选取2000个像素以及3000像素进行测试，像素值依次平均相差9.5与7.2。可见，本文提出改进后多元线性回归建模算法比传统建模算法相比，能够提供精确度更高的运算结果。

图3 算法实验结果

4 应 用

通过回归方程以及相关参数，用户对回归方程的拟合度进行分析，若回归方程的拟合度良好即可用于后续的去云、去噪等相关操作，否则用户应重新选择参数与范围进行回归方程拟合。本文将改进后的模型应用于去云处理，并通过用生成影像中的某一块区域替代因变量影像中被云层遮盖的区域实现去云后效果。若要进行去噪处理，则继续求出因变量影像与预测影像的残差影像，分别对两块影像利用小波进行空间去噪处理。最后将重新获得的两块数据进行相加得到最终的去噪图像。

如高分辨率遥感影像图4(a)中东部地区大部分为云层所覆盖。为进行去云处理，选取该地区多幅不同时相的影像，通过检测分别选取待去云影像中无云区域的每一个波段与多幅不同时相影像中对应区域的对应波段，基于改进后的多元线性回归建模算法建立回归方程，分别得出3个波段的拟合度最高的方程与其相对应的影像，其复相关系数分别为0.91、0.93、0.95。然后求出待去云影像的云层覆盖区域所有像素点的值，最后进行图形镶嵌，得到无云影像图，如4(b)所示。建模算法以遥感影像的所有像素点作为数据组进行分析，在最大程度上保证了模型的精确度。

图4 遥感影像去云

作为比较，按照传统随机取点的方法建立回归模型，在整个影像的全图范围中随机选取1000个像素点建立回归模型，平均像素值相差5.65。再通过两个回归模型生成的无云区域的预测影像分别与待去云影像的无云区域影像像素值相减生成残差影像，结果显示改进后模型的残差影像更加接近于全黑，即接近于全零像素。通过计算可得，改进后的模型生成的影像与待去云影像平均相差3.4像素值，小于原模型的6.3像素值。经实验，对去噪处理也可得到相似结果。

5 结束语

本文提出基于高分辨率遥感影像的多元线性回归模型的建立算法，采用等宽规则划分、分步读取和统一计算的方案改进模型使遥感影像的每个像素点都参与模型建立的运算，确保模型准确度。通过开发基于Web服务的多元线性回归在线分析软件及算法实验，成功地建立回归模型并得到回归参数，能够应用于高分辨率遥感影像处理，精确度优于传统建模算法。本改进后的建模算法可用于去云、去噪和矫正等遥感图像处理。基于SOA和Web服务实现的建模算法软件工具可推广、易集成。

建模算法具有一定的局限性，在对同一地域的多幅遥感影像建立多元线性回归模型时，因缺乏具体的数值数据，需要用户对遥感影像具有一定的基础与了解。待处理的不同遥感影像应该是同一地域和分辨率的影像，条件苛刻。分析的结果并不能够完全作为决策的依据，只能作为辅助决策的一种手段。今后研究中将进行建立多元线性回归模型的算法效率的改进，在兼顾空间与时间的基础上提高算法运行速度，并对多元线性回归模型在高分辨率遥感影像处理领域中的应用做进一步探索。

[1] 于小林，文建国，郁建林，等.基于分段线性回归的水质遥感图像校正算法[J].遥感信息，2010，25(6)：39-43.

[2] 吴炜，骆剑承，沈占锋，等.分类线性回归的Landsat影像去云方法[J].武汉大学学报(信息科学版)，2013，38(8)：983-987.

[3] 徐东，孙蕾，罗建书，等.基于多元线性回归的高光谱遥感图像小波去噪[J].遥感信息，2013，28(6)：78-81，86.

[4] 熊育久，曾爽，吴秀芹，等.基于统计学理论的内陆水质遥感反演进展[J].遥感信息，2008，23(3)：92-98.

[5] 胡彩平，秦小麟.融合空间自相关的空间数据预测模型[J].吉林大学学报(信息科学版)，2009，27(6)：601-606.

[6] JAJO K N.A review of robust regression and diagnostic procedures in Linear Regression[J].Acta Mathematicae Applicatae Sinica，2005，21(2)：209-224.

[7] XU D，SUN L，LUO J.Denoising of hyperspectral remote sensing image using multiple linear regression and wavelet shrinkage[C].Proceedings of 2013 International Conference on Information，Business and Education Technology (ICIBET-13)，Beijing，Mar，2013：152-155.

[8] 王卫安，王伟，乔刚.高分辨率卫星影像数据操作平台的建立与立体量测[J].测绘与空间地理信息，2010，33(6)：56-63.

[9] GILARDI N.Local machine learning models for spatial data analysis[J].Journal of Geographic Information and Decision Analysis，2000，4(1)：11-28.

[10] 刘严.多元线性回归的数学模型[J].沈阳工程学院学报(自然科学版)，2005(Z1)：128-129.

[11] 唐燕武.线性回归模型参数估计的几种方法[J].安庆师范学院学报(自然科学版)，2004，10(4)：74-77.

[12] 鲁铁定，陶本藻，周世健.基于整体最小二乘法的线性回归建模和解法[J].武汉大学学报(信息科学版)，2008，33(5)：504-507.

[13] 薛素静，上官同英.多元线性回归算法的研究和应用[J].水利电力机械，2007，29(5)：59-60.

An Approach for Modeling Multiple Linear Regression of High-resolution Remote Sensing Imagery

MENG Xiao-liang，SU Jun-long，WANG Shuai，YANG Xiao

(WuhanUniversity，Wuhan430079)

This paper proposes an approach for establishing multiple linear regression models to ensure that each pixel of remote sensing images are involved in，by using regularly division，step by step reading and unified computing.According to the model and its establishing algorithm，we designed and realized a Web service-based analysis software.Through testing，the result image predicted by the regression model is more accurate than the original，and can be successfully used in the regression model for high resolution remote sensing image processing.The improved multiple linear regression models and its establishing algorithm could be used in remote sense image processing such as cloud removing and de-noise.

remote sensing；high spatial resolution；multiple linear regression；model；regularly division

2014-04-28

2014-11-15

国家重大科技专项高分辨率对地观测系统项目(30-Y20A02-9003-12/13)；武汉大学自主科研项目(2042014kf0086)；武汉大学教学改革研究项目(2014054)。

孟小亮(1981—)，男，副教授，博士，主要研究方向为空间信息与传感器网。

E-mail：xmeng@whu.edu.cn

粟骏龙(1988—)，男，博士研究生，主要从事空间信息数据挖掘研究。

E-mail：4688812@163.com

10.3969/j.issn.1000-3177.2015.05.006

TP79

A

1000-3177(2015)141-0037-05